🕹️

M5Stack でゲームを作る 002

2022/05/27に公開3件

M5Stack

gamedev

tech

前回の記事

前回は単純なゲームループについて説明しました。
今回はいよいよゲームを作っていきます。

Breakout(ブロック崩し)

いわゆる古典ゲームであるブロック崩しを作っていきます。
簡単なように見えて品質を上げようとすると考慮すべき点が多い、意外と難易度が高いタイトルではないかと思います。
とはいえ、物理演算でがっちり計算してもよし、代替計算で軽量に仕上げてもよし、いろいろな手法を試すという意味では良い教材になり得るのではないでしょうか?

ゲームと嘘

昨今のハードは性能が素晴らしく良くなって、昔は高負荷高コストだった計算を難なくこなせるようになりました。
それは大変喜ばしい事なのですが、それ故にリアルに寄せすぎて物理演算と継続的衝突判定を真面目にやりすぎたり、どうでもいいオブジェクトに大量のポリゴンを割いて処理負荷が発生したりと、実装コストと出来上がった表現が見合っていないゲームもちらほら見かけます。
ゲームはシミュレーターではないので、見た目や挙動に違和感を感じさせない範囲でいくらでも嘘をついて良いのだと私は思います。
コスト(人、金、時間)や、優先度、ゲームデザイン等を考えた上で実装手法を適切に選択したいものです。

今回は厳密な物理演算を用いる事なく、ゲームとしてある程度の嘘を許容する方向で作っていきます。

ボール

真円として定義します。

位置と移動方向と移動スピード

現在の中心位置、方向ベクトル(正規化済=>単位ベクトル=>大きさ 1 )、スピード、半径を定義します。
座標系はスクリーン座標系と同じものとします (X 正方向が右、Y 正方向が下)

using Vec2 = goblib::shape2d::Vector2<float>;
class Ball
{
  public:
    constexpr std::int16_t RADIUS = 2; // ボール半径
  protected:
    Vec2 _center;    // 中心座標
    Vec2 _v;         // 移動方向ベクトル(正規化済)
    float _velocity; // 移動スピード
};
// 1 フレームに1回呼ばれる更新処理
void Ball::update()
{
    _center += _v * _velocity; // 次のフレームの中心位置
}

衝突判定

様々な手法があります。

移動後の中心座標を用いた内外判定
移動後のバウンディングボックスを用いた重なりの検出による判定
移動前後のベクトルを用いた交差による判定
移動前後をカプセル形状として交差判定

等…

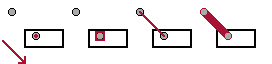
図A : 左から 1, 2, 3, 4 の手法

今回は古典的な手法 1、ボールを点、パドルやブロックを矩形とみなして実装していきます。

トンネリング

手法 1,2 では移動速度が対象物の幅より大きい場合、トンネリング(すり抜け)が発生します。

図B : 1,2 では移動後の点や矩形からは交差したか判定できない

移動後位置のみでの判定では衝突が検出できません。
対処するための手法にも様々なものがありますが、ここでは処理を分割する事でトンネリングを防ぎます。
いわゆる連続的衝突判定(CCD Continuous Collision Detection)ですね。

_velocity が 4 だとすると次のフレームの位置の算出は以下のように分割できます。
分割の都合上、_velocity は整数に変更します。

_center += _v * 4; // 移動距離 4
// 分割すると
_center += _v; // 移動距離 1
_center += _v; // 移動距離 1
_center += _v; // 移動距離 1
_center += _v; // 移動距離 1
// 移動距離合計は 4

分割された各処理での移動距離は 1 なので、すり抜ける事なく衝突が検出できるはずです。

class Ball
{
    // 中略
    int _velocity; // 移動スピード
};

// 1回呼ばれると _velocity 分移動する
void Ball::update()
{
    auto cnt = _velocity;
    Vec2 ov;
    Vec2 nv = _center;
    while(cnt--)
    {
        ov = nv;
        nv = ov + _v;
        _update(ov, nv); // *1
    }
    _center = nv;
}

// *1 1回呼ばれると _v だけ移動する
void Ball::_update(Vec2& ov, Vec2& nv)
{
	// 衝突で _v を更新する
	.
	.
	.
	
	nv = ov + _v; // 移動後位置の更新
}

この手法を採用すると、移動スピードが整数に限定されるという制約が生じますが、これを許容します。

ゲームフィールド

ブロック崩しでは矩形のゲームフィールドが設定される事が多く、ボール位置が下辺を超えた場合にボールが失われるルールが一般的です。
ここでも一定の矩形範囲を設定し、ゲームフィールドとして設定します。
中心位置から計算毎に半径を足し引きするのが煩わしいので、描画用のフィールド矩形とは別に当たり判定用の矩形を持つ事にします。

using Rect2 = goblib::shape2::Rectangle<std::int16_t>;
// Field of playing(for render)
constexpr Rect2 FIELD_RECT(0,32, 320, 240 - 32);
// Field of playing(for collision)
constexpr Rect2 FIELD_HIT_RECT(FIELD_RECT.left() + Ball::RADIUS, FIELD_RECT.top() + Ball::RADIUS,
                               FIELD_RECT.width() - Ball::RADIUS * 2, FIELD_RECT.height() - Ball::RADIUS * 2);

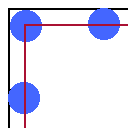
図C : ゲームフィールドの描画矩形(黒)と当たり矩形(赤)、ボール(青)

角においてはボールの半径が大きいほど不正確になる局面がありますが、ゲーム上の嘘とします。

パドル

横長矩形で、フィールドの一定の高さを左右移動し、ボールが当たると跳ね返るものとします。
フィールドと同様にボール半径を考慮した当たり用の矩形を準備します。
フィールドとは逆に半径分大きくしたものが当たり矩形となります。

class Paddle
{
	// ...省略...
  private:
    Rect2 _rect; // 描画用
    Rect2 _hitRect; // 当たり用
}
_hitRect = Rect2(_rect.left() - Ball::RADIUS, _rect.top() - Ball::RADIUS, _rect.width() + Ball::RADIUS * 2, _rect.height() + Ball::RADIUS * 2);

操作は以下のボタンを使用します。

ボタン	入力	挙動
Faces 十字左本体Aボタン	押下	パドルを左へ移動
Faces 十字右本体Cボタン	押下	パドルを右へ移動
Faces B ボタン本体 B ボタン	押下	パドルの移動を加速(押している間) ゲーム開始時の玉の始動

入力の取得

Face GB 入力を取得するためのインスタンスを準備し、アプリケーションクラスの update() で入力を処理します。
本体ボタンは M5 を使用します。

app.hpp

#include <gob_m5s_faces.hpp>
class Breakout : public goblib::App<AppClock, MAX_FPS, MAX_FPS>, goblib::Singleton<Breakout>
{
	// ...省略...
    goblib::m5s::FaceGB _input;
}

app.cpp

void Breakout::update(float delta)
{
    M5.update();
    _input.pump();

    // 0x01:left 0x02:rapid 0x04:right
    std::uint8_t mbit = (M5.BtnA.isPressed()) | (M5.BtnB.isPressed() << 1) | (M5.BtnC.isPressed() << 2) |
                        (_input.isPressed(goblib::m5s::FaceGB::Button::Left) ? 1 : 0) |
                        (_input.isPressed(goblib::m5s::FaceGB::Button::Right) ? 4 : 0) |
                        (_input.isPressed(goblib::m5s::FaceGB::Button::B) ? 2 : 0);

    std::int16_t ox = 0; // パドルの水平方向移動増分
    if(mbit & 0x01) { ox -= 4 + 2 * ((mbit & 0x02) != 0); }
    if(mbit & 0x04) { ox += 4 + 2 * ((mbit & 0x02) != 0); }
    paddle.offset(ox, 0); // パドルの移動関数
}

M5.btnX.isPressed() は uint8_t の 1 or 0 を返しますが、 goblib::m5s::FaceGB::isPressed() は bool を返すので注意。
反する方向が入力された場合はどちらにも動かないようにしておくと良いでしょう。

ブロック^[1]

矩形として定義され、ボールが当たるとボールは反射し、ブロックの耐久力がなくなったら消えるものとします。また不死身のブロックもありとします。
パドルと同様に当たり用矩形も用意します。

class Bricks
{
  public:
    class Brick
    {
      public:
        constexpr static std::int16_t WIDTH = 16;
        constexpr static std::int16_t HEIGHT = 8;
        enum Type : std::uint8_t { None/*0*/, Clr1, Clr2, Clr3, Clr4, Clr5, Clr6, Clr7, Clr8, Unbreakable/*9*/ };
        Brick(std::int16_t x, std::int16_t y, std::uint8_t type);
        // 中略
      private:
        std::uint8_t _type;
        std::int8_t _life;
        Rect2 _rect, _hitRect;
    };
    std::vector<Brick> _vector;
    // 中略

各要素を加味したボールの更新

構成要素が出揃ったので、ボールの更新は以下のようになります。

void Ball::update(Paddle& paddle, Bricks& bricks)
{
    auto cnt = _velocity;
    Vec2 ov;
    Vec2 nv = _center;
    while(cnt--)
    {
        ov = nv;
        nv = ov + _v;
        _update(ov, nv, baddle, bricks);
    }
    _center = nv;
}
void Ball::_update(Vec2& ov, Vec2& nv, Paddle& paddle, Bricks& bricks)
{
    // 略
}

衝突と反射

ボールとゲームフィールド内の反射

ボールの移動予定位置とフィールドの各辺を比較する。
はみ出るなら移動方向を変更する
移動方向は逆転させるのではなく左側にはみ出ていたら右方向、右側にはみ出ていたら左方向という様にフィールド内へ向かう方向とします。
(今後パドルやブロックとの反射によってはみ出た位置からはみ出た位置への移動が発生した場合でも、フィールド内への移動となるのでボールが行方不明になりにくくなります)
1.全ての辺との判定が終了したら、新しい位置を更新する

角においては複数の辺と衝突する場合があるので、辺全てとの比較を通るようにします。

void Ball::_update(Vec2& ov, Vec2& nv, Paddle& paddle, Bricks& bricks)
{
    if(nv.x() < FIELD_HIT_RECT.left()) // 左壁
    {
        _v.move(std::abs(_v.x()), _v.y());
    }
    if(nv.x() > FIELD_HIT_RECT.right()) // 右壁
    {
        _v.move(-std::abs(_v.x()), _v.y());
    }
    // else if(...) ではダメ!
    if(nv.y() < FIELD_HIT_RECT.top()) // 上壁
    {
        _v.move(_v.x(), std::abs(_v.y()));
    }
	nv = ov + _v;
}

ボールとパドルとの反射

フィールドとの反射は静止矩形との計算でした。パドルは移動する矩形です。
移動体同士の衝突は正確にやろうとすると互いの移動を考慮して接触する地点を特定する必要がありますが、ここはゲーム的な嘘を許容する方向とし、パドルの移動後に対してボールとの衝突を検出するものとします。
またパドルとボールの接触位置によって反射角度に変化をつける事でプレイヤーの技術介入を促します。
上下方向からの反射では中心に近いほど鋭角的、遠いほど鈍角的になるのがよくある実装です。

A. atan2

単純な手法としては、接触した位置とパドルの中心との差分から成る角度へ反射させる方法があります。 atan2(y, x) の出番ですね。
パドルの大きさに依存しますが、かなりの範囲の方向が得られます。

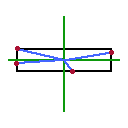
図D : パドル中心と接触位置(赤丸)からなる角度(青線)

問題点

当たった位置によっては水平(真右/真左)方向にボールが移動してしまいます。その場合延々と壁とパドルとの反射が続き、ゲームとして成り立たなくなってしまいます。上方向に向かうようにするか^[2]、角度制限をつける等の補正をした方が良いでしょう。
垂直方向も気になるなら同様の補正を施しましょう。

namespace
{
// pos は r 内にあるか?
bool contains(const Rect2& r, const Vec2& pos)
{
    return std::isgreaterequal(pos.x(), r.left()) && std::islessequal(pos.x(), r.right()) &&
            std::isgreaterequal(pos.y(), r.top()) && std::islessequal(pos.y(), r.bottom());
}
}
void Ball::_update(Vec2& ov, Vec2& nv, Paddle& paddle, Bricks& bricks)
{
    auto pr = paddle.hitRect(); // 当たり矩形取得
    if(contains(pr, nv))
    {
        int xd = nv.x() - pr.center().x();
        int yd = nv.y() - pr.center().y();
        if(yd == 0) { yd = -1; } // 水平にならないように上方向に補正
        auto radian = std::atan2(yd, xd);
        _v.move(std::cos(radian), std::sin(radian)); // 移動方向更新
    }

しかしこの方法だとパドル操作で狙った方向ボールを打ち返すのが困難です。特に同じ方向に反射させたい場合、ドット単位でのパドルの位置合わせが必要となります。
そこで反射方向の算出を変更し、プレイヤーの技術介入をしやすくします。

B. 分割マス判定

パドル側当たり矩形を column x row マスに分割し、当たった位置に応じた値を使う手法です。
マス目の粒度と設定された値によって、ゲームバランスが変化しますのでこの辺りは好みのサジ加減で調整してみてください。
atan2 と違いボールの移動方向が数種に固定化されるので、挙動の確認や調整はしやすいでしょう。

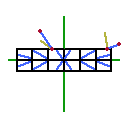
図E : パドル辺り矩形を 6 x 2 に分割し、各マスに固定の角度を設定する

パドルの幅と高さは 32 x 8 、ボール半径が 2 なら当たり矩形は 36 x 12 となるので、これを 12 x 2 マスに分割していきます。
テーブル引きは絶対値を使う事で 6 x 1 マス分のテーブルで賄います。象限反転は計算で求めます。

// 分割数
constexpr std::int16_t PADDLE_DIV_HOR = 6;
constexpr std::int16_t PADDLE_DIV_VER = 1;
// 分割位置算出の為の幅と高さ
constexpr std::int16_t PADDLE_DIV_WIDTH = ((Paddle::WIDTH + Ball::RADIUS * 2) / 2) / PADDLE_DIV_HOR;
constexpr std::int16_t PADDLE_DIV_HEIGHT = ((Paddle::HEIGHT + Ball::RADIUS * 2) / 2) / PADDLE_DIV_VER;
// 角度テーブル (X/Y正方向) [0]:真ん中より ... [n]:端より
constexpr float refTable[PADDLE_DIV_HOR * PADDLE_DIV_VER] =
{
    goblib::math::deg2rad(11.25f * 7),
    goblib::math::deg2rad(11.25f * 6),
    goblib::math::deg2rad(11.25f * 5),
    goblib::math::deg2rad(11.25f * 4),
    goblib::math::deg2rad(11.25f * 3),
    goblib::math::deg2rad(11.25f * 2),
};
void Ball::_update(Vec2& ov, Vec2& nv, Paddle& paddle, Bricks& bricks)
{
    auto pr = paddle.hitRect(); // 当たり矩形取得
    if(contains(pr, nv))
    {
        auto xd = nv.x() - pr.center().x();
        auto yd = nv.y() - pr.center().y();
        int xi = std::abs(xd) / PADDLE_HIT_WIDTH;
        int yi = std::abs(yd) / PADDLE_HIT_HEIGHT;

        float radian = refPaddleTable[ yi * PADDLE_HIT_HOR + xi];
        if(xd < 0) { radian = goblib::math::deg2rad(180.0f) - radian; } // 水平方向象限反転
        if(yd < 0) { radian = goblib::math::deg2rad(360.0f) - radian; } // 垂直方向象限反転
        radian = goblib::math::wrapRad(radian);

        _v.move(std::cos(radian), std::sin(radian)); // 移動方向更新
    }
    .
    .

ボールとブロックの反射

ブロックとの反射は静止矩形との計算となります。
方向ベクトルの変化は以下の通りとします。

上下辺との衝突	左右辺との衝突	角との衝突
垂直移動方向を逆へ水平方向は維持	垂直方向は維持水平移動方向を逆へ	垂直水平方向はブロック中心から遠ざかる方向へ

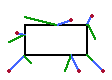
図F : ブロックとの反射

バドルとの衝突反射で使用した分割判定を流用します。粒度をそれなりにして、角の判定が大きくなりすぎないようにすると良いでしょう。
ブロックの大きさが 16 x 8 なら、当たり矩形は 20 x 12 となるので、これを 10 x 12 マスに分割していきます。
パドルと同様に絶対値を用いて 5 x 6 マス分のテーブルで賄います。
パドルと違い決まった角度を値としては利用できません。そこで処理の為のマジックナンバーをテーブルの値として設定し、分岐に利用します。

二進数 2 bit を用います。

00	01	10	11
ブロック中心から遠ざかる方向	X反転	Y反転	XY反転

複数同時衝突

ブロックの構成、ボールの移動によって複数のブロックと同時に衝突する場合があります。最大で 3 個同時まで考えられます。

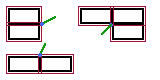
図G : 複数のブロックとの衝突赤は当たり矩形

同時衝突を無視して最初に衝突判定されたブロックのみで判定してもよいのですが、ここはブロックの当たり矩形を合成して対処してみます。

衝突検出されたブロックの当たり矩形を合成すると以下の図のようになります。

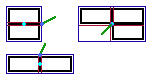
図H : 当たり矩形の合成(青) とその中心(水色)

合成矩形の中心を分割位置算出の基準点として使用します。また 3 個同時の場合に対応するために、中心での接触の場合は移動方向を反転します。

// 分割数
constexpr std::int16_t BRICK_HIT_HOR = 5;
constexpr std::int16_t BRICK_HIT_VER = 6;
// 分割位置算出の為の幅と高さ
constexpr std::int16_t BRICK_HIT_WIDTH = ((Bricks::Brick::WIDTH + Ball::RADIUS * 2) / 2) / BRICK_HIT_HOR;
constexpr std::int16_t BRICK_HIT_HEIGHT = ((Bricks::Brick::HEIGHT + Ball::RADIUS * 2) / 2) / BRICK_HIT_VER;
// 処理の為のマジックナンバーテーブル [0]:中心より
constexpr std::uint8_t refBrickTable[BRICK_HIT_HOR * BRICK_HIT_VER] =
{
    0x03, 0x01, 0x01, 0x01, 0x01,
    0x02, 0x00, 0x01, 0x01, 0x01,
    0x02, 0x02, 0x00, 0x01, 0x01,
    0x02, 0x02, 0x02, 0x01, 0x01,
    0x02, 0x02, 0x02, 0x02, 0x00,
    0x02, 0x02, 0x02, 0x02, 0x00,
};
void Ball::_update(Vec2& ov, Vec2& nv, Paddle& paddle, Bricks& bricks)
{
    // 生存しているブロックのバウンディング内か? (処理の刈り込み)
    if(contains(bricks.bounding(), nv))
    {
        std::vector<Bricks::Brick*> hit;
        // 衝突するブロックの収集
        for(auto& e : bricks.vector()) 
        {
            if(!e.alive()) { continue; } // 消されているブロックは除外
            if(contains(e.hitRect(), nv)) { hit.push_back(&e); }
        }
        if(!hit.empty())
        {
            Rect2 br;
            // ブロックの当たり矩形を合成
            for(auto& e : hit)
            {
                br |= e->hitRect();
                e->hit(); // ブロックのライフを減らす等
            }
            auto xd = nv.x() - br.center().x();
            auto yd = nv.y() - br.center().y();
            int xi = std::abs(xd) / BRICK_HIT_WIDTH;
            int yi = std::abs(yd) / BRICK_HIT_HEIGHT;
            auto behavior = refBrickTable[ yi * BRICK_HIT_HOR + xi ];
            // 値に応じて処理
            if(behavior == 0)   { _v.move(goblib::math::sign(xd) * std::abs(_v.x()), goblib::math::sign(yd) * std::abs(_v.y()) ); }
            if(behavior & 0x01) { _v.move(-_v.x(), _v.y()); }
            if(behavior & 0x02) { _v.move(_v.x(), -_v.y()); }
        }
    }
    // 略

処理順番

フィールド、パドル、ブロックの処理順番を考えます。
最終的にフィールドから出て明後日の方向に行かないようにする為、フィールドとの判定は最後にするのがよいでしょう(移動反転ではない処理にした事でこの順番が生きてきます)。
パドルとブロックに関しては、ブロックの矩形がパドルの矩形が重ならない事を前提とし、パドル => ブロックの順に処理する事にします。

千日手

さて、残念な事にいわゆる千日手となる場合があります。

図I : 反射の繰り返しによる千日手

摩擦やボールの回転角等が考慮されていない以上、このように同じ動きを繰り返してゲームとして手詰まりな状況に陥っててしまうのです。

ちなみにかの大山のぶ代さんが愛したゲームにおいては、この状況の解決をゲームデザインと合わせて実にスマートな手法にて行っています^[3]
画面上部のハッチからいわゆるお邪魔キャラクターが定期的に登場するのです。これらのキャラクターはフィールドを這い回り、ボールと接触するとボールの移動方向が変動します。これによって千日手が解消されます。
この手法はゲームにゆらぎを与え、千日手を防ぎ、スコアアタックの一要素とするという、とても素晴らしい解決法だと思います。

今回は一定期間ボールがパドルに接触しなかった場合、次にボールがブロックに当たって反射した移動方向を変動させる事で解決します(突然脈絡もなく動きが変わるので美しくない手法ですが、お邪魔キャラの実装を避けたので)。なおパドルを介した千日手はプレイヤーがパドルを移動させる事で解消されるので対処しません。

// 略
if(_framesNotHittingPaddle >= NUMBER_OF_FRAMES_TO_FORCEANGLE_CHANGE)
{
    _framesNotHittingPaddle = 0;
    auto radian = std::atan2(std::abs(_v.y()), std::abs(_v.x()));
    if(radian > goblib::math::deg2rad(45.0f)) { radian -= goblib::math::deg2rad(11.25f); }
    else { radian += goblib::math::deg2rad(11.25f); }
    if(std::isless(_v.x(), 0.0f)) { radian = goblib::math::deg2rad(180.0f) - radian; }
    if(std::isless(_v.y(), 0.0f)) { radian = goblib::math::deg2rad(360.0f) - radian; }
    radian = goblib::math::wrapRad(radian);
    _v.move(std::cos(radian), std::sin(radian));
}
// 略

ソース

以上を踏まえたてまとめたものがこちらになります。
残機、スコアを追加してゲームてしての体裁を最低限整えました。

あとがき

ブロック崩しの実装手法には他にも様々ものがありますし、今回の手法も改善、改良の余地があります。また今の所単純な図形描画しか用いていない上に効果音等もなく貧相です。
次回以降今回のブロック崩しをベースに、画像と音のリソースを加えてゴージャスにしていければと思います。

脚注

日本ではブロックと呼ばれる事が多いですが、Breakout では伝統的に Brick(レンガ) と呼ばれる事が多いようです。 ↩︎
下方向に補正しても脱せますが、プレイヤーにとっては不利な方向への修正となるのでここでは採用しません。 ↩︎
当該ゲームにおいて千日手がある、と仮定した上での考察です。 ↩︎

Discussion

GOB

う、画像が一部でてないので修正します(´･ω･`)

GOB

修正版あげました

GOB

goblib は version 0.1.1 以降を使用してください。