Goals Tech BlogPublicationへの投稿
😊

回帰モデルの評価指標について考えてみる

Kei TAKAHATA
に公開
機械学習
評価指標
回帰分析
tech

はじめに

時系列予測モデルの精度改善に勤しんでいるAIエンジニアです。

モデルの良し悪しを判断するための評価指標選びって大事ですよね。

代表的な指標もありますが、

使ってみると直感と合わない結果になっていたり、

かといって複数の指標を使うと

Aという指標では改善したけどBという指標では悪化してしまった、、、

となったりして、

で、どっちが良いの？

となります。

アプリやビジネスによっても重視すべき項目が変わるので最終的には要件ごとに選ばなければならないのですが、今回は回帰モデルの代表的な評価指標に対して主観を交えつつ書き連ねていこうと思います。

評価指標と主観コメント

RMSE: Root Mean Squared Error（二乗平均平方根誤差）

数式

\mathrm{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}

解釈

誤差（y_i - \hat{y}_i）の二乗の平均を計算し、スケールを合わせるために平方根を取る。

コメント

回帰モデルの評価指標の王道の印象。

個人的に指標の改善・悪化が直感とも一致する。
誤差の二乗にペナルティが発生するため、大きな外れを重視できる。
（逆に言うと小さな外れに注目したい場合は使わない方が良い。）

RMSEの大きさがデータセットのスケールに依存するので、複数のデータセットを横断した比較がしにくい。
大きな外れを重視する分、誤差の外れ値の影響も受ける。

コード

RMSEの計算
def calculate_rmse(df: pd.DataFrame, actual_column: str, predicted_column: str) -> float:
    """
    RMSE（Root Mean Square Error）を計算する関数
    RMSE = sqrt(1/n * sum((y - y_hat)^2))

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名

    Returns
    -------
    float
        RMSEの値
    """
    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]

    # 差の二乗を計算
    squared_error = error ** 2

    # 平均を計算
    mean_squared_error = squared_error.mean()

    # 平方根を計算
    rmse = np.sqrt(mean_squared_error)

    return rmse

RMSPE: Root Mean Squared Percentage Error（平均二乗パーセント誤差の平方根）

数式

\mathrm{RMSPE} = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} \left( \frac{y_i - \hat{y}_i}{y_i} \right)^2 }

解釈

誤差（y_i - \hat{y}_i）の割合の二乗の平均を計算し、スケールを合わせるために平方根を取る。

コメント

誤差をパーセントで評価できるので、スケールの異なるデータセット間でも比較しやすい。

小さい値の誤差に敏感すぎる。
0に近い値があると指標が極端に大きくなる。（そもそも0の場合は無限大になる。）

コード

RMSPEの計算
def calculate_rmspe(df: pd.DataFrame, actual_column: str, predicted_column: str) -> float:
    """
    RMSPE（Root Mean Square Percentage Error）を計算する関数
    実績値が0の場合は計算できないため、0の行を削除して計算
    RMSPE = sqrt(1/n * sum((y - y_hat) / y)^2)

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名

    Returns
    -------
    float
        RMSPEの値
    """
    # 実績値が0の場合は計算できないため、0の行を削除
    df = df[df[actual_column] != 0].copy()

    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]
    error_rate = error / df[actual_column]
    squared_error_rate = error_rate ** 2

    # 平均を計算
    mean_squared_error_rate = squared_error_rate.mean()

    # 平方根を計算
    rmspe = np.sqrt(mean_squared_error_rate)

    return rmspe

NRMSE: Normalized RMSE（正規化RMSE）

RMSE正規化時の分母は様々な複数ありますが、ここでは実績値の平均で正規化する方法を記載しておきます。

数式（平均で割る場合）

\begin{aligned} \mathrm{NRMSE} &= \frac{1}{\bar{y}} \cdot \mathrm{RMSE} \\\\ &= \frac{1}{\bar{y}} \cdot \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 } \\\\ \end{aligned}

解釈

RMSEを実績値の平均（\bar{y}）で割ることで、誤差を平均値に対する割合とする。

コメント

誤差の割合のため、複数データセットで比較できる。
実績値が0を含んでいても計算可能で、RMSPEやMAPEよりも実務で使いやすい。
誤差が平均値の何倍かを直感的に把握できる。

平均値が極端に小さい場合は値が大きくなりやすい。

コード

NRMSEの計算
def calculate_nrmse(
    df: pd.DataFrame,
    actual_column: str,
    predicted_column: str,
    denominator: str = "mean"
) -> float:
    """
    NRMSE（Normalized Root Mean Square Error）を計算する関数
    デフォルトでは平均値を分母に使用
    平均使用時の数式: NRMSE = (1 / mean(y)) * sqrt(1/n * sum((y - y_hat)^2))
    最大値最小値使用時の数式: NRMSE = (1 / (max(y) - min(y))) * sqrt(1/n * sum((y - y_hat)^2))
    標準偏差使用時の数式: NRMSE = (1 / std(y)) * sqrt(1/n * sum((y - y_hat)^2))
    IQR使用時の数式: NRMSE = (1 / IQR(y)) * sqrt(1/n * sum((y - y_hat)^2))

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名
    denominator : str, optional
        正規化に使う分母の種類（"mean", "min_max", "std"）

    Returns
    -------
    float
        NRMSEの値
    """
    y = df[actual_column]
    if denominator == "mean":
    # 実測値の平均を計算
        denominator_value = y.mean()
    elif denominator == "min_max":
        denominator_value = y.max() - y.min()
    elif denominator == "std":
        denominator_value = y.std()
    elif denominator == "iqr":
        denominator_value = y.quantile(0.75) - y.quantile(0.25)
    else:
        raise ValueError("denominator must be 'mean', 'min_max', 'std', or 'iqr'")

    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]

    # 差の二乗を計算
    squared_error = error ** 2

    # 差の二乗の平均を計算
    mean_squared_error = squared_error.mean()

    # 平方根を計算
    rmse = np.sqrt(mean_squared_error)

    # NRMSEを計算
    nrmse = rmse / denominator_value

    return nrmse

MAE: Mean Absolute Error（平均絶対誤差）

数式

\mathrm{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|

解釈

誤差（y_i - \hat{y}_i）の絶対値の平均。

コメント

誤差の絶対値で評価するため、誤差二乗にペナルティを付与する指標よりも誤差の外れ値に強い。
MAEの大きさがデータセットに依存するので、複数のデータセットがある場合は比較できない。

時系列予測などで曜日ごとにスケールがわかる場合（例えば、平日よりも土日の売上の方がスケールが大きい）、土日の追従ができなくても高評価になりがち。
直感と合わない結果になる。

コード

MAEの計算
def calculate_mae(df: pd.DataFrame, actual_column: str, predicted_column: str) -> float:
    """
    MAE（Mean Absolute Error）を計算する関数
    MAE = 1/n * sum(|y - y_hat|)

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名

    Returns
    -------
    float
        MAEの値
    """
    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]

    # 差の絶対値を計算
    absolute_error = np.abs(error)

    # 平均を計算
    mean_absolute_error = absolute_error.mean()

    return mean_absolute_error

MAPE: Mean Absolute Percentage Error（平均絶対パーセント誤差）

数式

\mathrm{MAPE} = \frac{100}{n} \sum_{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right|

解釈

誤差（y_i - \hat{y}_i）の割合の平均を計算し、%で表すために100を掛ける。

コメント

MAEと同じで誤差の絶対値で評価するため、誤差二乗にペナルティを付与する指標よりも誤差の外れ値に強い。
指標が割合のため、複数データセットで比較できる。
割合でズレの大きさがわかるためビジネスサイドにも説明しやすい。

0に近い値があると指標が極端に大きくなる。（そもそも0の場合は無限大になる。）
MAEと同じで時系列予測などで曜日ごとにスケールがわかる場合、土日の追従ができなくても高評価になりがち。
直感と合わない結果になる。

コード

MAPEの計算
def calculate_mape(df: pd.DataFrame, actual_column: str, predicted_column: str) -> float:
    """
    MAPE（Mean Absolute Percentage Error）を計算する関数
    MAPE = 100 * 1/n * sum(| (y - y_hat) / y |)

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名

    Returns
    -------
    float
        MAPEの値
    """
    # 実測値が0の場合は0除算になるので、0の行を削除
    df = df[df[actual_column] != 0].copy()

    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]
    error_rate = error / df[actual_column]

    # 絶対値の比率を計算
    absolute_error_rate = np.abs(error_rate)

    # 平均を計算
    mean_absolute_error_rate = absolute_error_rate.mean()

    # 100を掛けてパーセントに変換
    mape = 100 * mean_absolute_error_rate

    return mape

SMAPE: Symmetric Mean Absolute Percentage Error（対称平均絶対パーセント誤差）

数式

\mathrm{SMAPE} = \frac{100}{n} \sum_{i=1}^{n} \frac{2 \cdot |y_i - \hat{y}_i|}{|y_i| + |\hat{y}_i|}

解釈

誤差（y_i - \hat{y}_i）の割合を予測結果（\hat{y}_i）も使用して計算する。その平均を計算し、%で表すために100を掛ける。

コメント

MAPEの弱点（0付近で暴れる）を補うために考案された指標。
基本的にMAPEと同じ印象。

値が0に近い場合でも安定しやすいが、分母が小さいと（実績も予測結果も0に近い場合）やはり不安定になる。

コード

SMAPEの計算
def calculate_smape(df: pd.DataFrame, actual_column: str, predicted_column: str) -> float:
    """
    SMAPE（Symmetric Mean Absolute Percentage Error）を計算する関数
    SMAPE = 100 * 1/n * sum(| (y - y_hat) / ( |y| + |y_hat| ) / 2 |)

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名

    Returns
    -------
    float
        SMAPEの値
    """

    # 実測値と予測値の絶対値を計算
    absolute_actual = np.abs(df[actual_column])
    absolute_predicted = np.abs(df[predicted_column])

    # 実測値と予測値の絶対値の合計が0の場合は0除算になるので、0の行を削除
    df = df[absolute_actual + absolute_predicted != 0].copy()

    # 0の行を削除した後の実測値と予測値の絶対値を再計算
    absolute_actual = np.abs(df[actual_column])
    absolute_predicted = np.abs(df[predicted_column])

    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]

    # 絶対値の比率を計算
    absolute_error_rate = 2 * np.abs(error) / (absolute_actual + absolute_predicted)

    # 平均を計算
    mean_absolute_error_rate = absolute_error_rate.mean()

    # 100を掛けてパーセントに変換
    smape = 100 * mean_absolute_error_rate

    return smape

MASE: Mean Absolute Scaled Error（平均絶対スケールド誤差）

数式

\mathrm{MASE} = \frac{\frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|}{\frac{1}{n-1} \sum_{i=2}^{n} |y_i - y_{i-1}|}

解釈

常に1時点前の値（y_{i-1}）を予測値をする別のモデル（ナイーブ予測）があることを仮定し、誤差（y_i - \hat{y}_i）の絶対値の平均が相対的に改善したか？を見る。
（1より大きい場合、1時点前の結果を予測結果とする方が良いことになる。）

コメント

時系列予測でよく使われる。
スケールに依存しないので、複数のデータセットで比較できる。

1時点前の予測をするモデルとの相対評価になってしまうので、値を見ても解釈が難しい。

コード

MASEの計算
def calculate_mase(df: pd.DataFrame, actual_column: str, predicted_column: str, m: int = 1) -> float:
    """
    MASE（Mean Absolute Scaled Error）を計算する関数
    MASE = (1/n) * sum(|y - y_hat| / ( (1 / (n-1)) * sum(|y - y_i-1|)))

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名
    m : int, default 1
        季節性周期（非季節系列の場合は1）

    Returns
    -------
    float
        MASEの値
    """
    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]

    # 実測値と予測値の差の絶対値を計算
    absolute_error = np.abs(error)

    # 実測値と予測値の差の絶対値の平均を計算
    mean_absolute_error = absolute_error.mean()

    # naive法のMAE（ラグm差分の平均絶対値）
    if len(df[actual_column]) <= m:
        raise ValueError("データ数が季節性周期m以下のため、MASEを計算できません。")
    mae_naive = np.mean(np.abs(df[actual_column].values[m:] - df[actual_column].values[:-m]))

    # MASEを計算
    mase = mean_absolute_error / mae_naive

    return mase

R²: Coefficient of Determination（決定係数）

数式

R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}

解釈

常に平均値（\bar{y}）で予測するモデルがあると仮定し、誤差（y_i - \hat{y}_i）の二乗の合計が相対的に改善したか？を見る。
一般的には（常に平均値を予測結果とするモデルよりも）誤差が小さくなるはずなので、\frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}は小さいほど良いという結果となる。
1から引くことで大きいほど良いという指標にしている。
誤差が0の場合は最大値の1となる。
（マイナスになってしまう場合、平均で予測した方が誤差が小さくなるということになる。）

コメント

今まで挙げた誤差を表現する指標と異なり、値が大きいほど良いと判断する指標。

スケールに依存しないので、複数のデータセットで比較できる。

良し悪しはわかるが値を見てもどの程度ズレるのか？の説明がしにくく、ビジネスサイドへの説明もしづらい。

コード

R^2の計算
def calculate_r2(df: pd.DataFrame, actual_column: str, predicted_column: str) -> float:
    """
    R^2（決定係数）を計算する関数
    R^2 = 1 - (sum((y - y_hat)^2) / sum((y - y_mean)^2))

    Parameters
    ----------
    df : pd.DataFrame
        データフレーム
    actual_column : str
        実測値の列名
    predicted_column : str
        予測値の列名

    Returns
    -------
    float
        R^2の値
    """

    # 実測値の平均を計算
    y_mean = df[actual_column].mean()

    # 実測値と平均の差の二乗の合計（全変動）を計算
    diff_mean_squared = (df[actual_column] - y_mean) ** 2
    total_sum_of_squares = diff_mean_squared.sum()

    # 実測値と予測値の差を計算
    error = df[actual_column] - df[predicted_column]

    # 実測値と予測値の差の二乗を計算
    squared_error = error ** 2

    # 実測値と予測値の差の二乗の合計（残渣平方和）を計算
    sum_of_squared_errors = squared_error.sum()

    # R^2を計算
    r2 = 1 - (sum_of_squared_errors / total_sum_of_squares)

    return r2

データでの比較

簡単なテストデータを使用してそれぞれの指標の結果を確認してみます。
テストデータとして以下のデータを用意します。

2025-06-02の月曜日から1週間分のデータを用意しています。
月曜日から木曜日よりも金曜日、金曜日よりも土日が伸びるようにしています。

date y predicted_1 predicted_2
2025-06-02 10 10 7
2025-06-03 12 13 15
2025-06-04 0 1 2
2025-06-05 13 12 10
2025-06-06 20 18 23
2025-06-07 60 55 65
2025-06-08 50 40 55

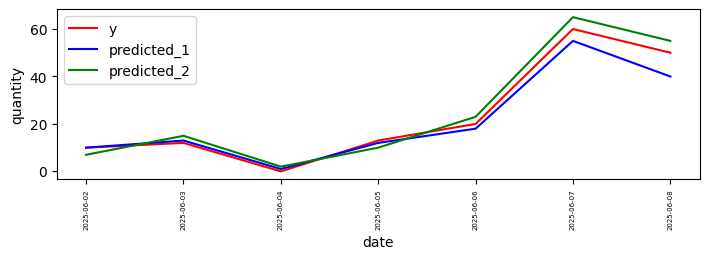
グラフにすると以下のようになります。

赤: 正解
青: predicted_1
緑: predicted_2

それぞれの指標の結果は

指標 predicted_1 predicted_2 良いモデル
RMSE 4.34 3.59 predicted_2
RMSPE 0.11 0.20 predicted_1
NRMSE_mean 0.18 0.15 predicted_2
MAE 2.86 3.43 predicted_1
MAPE 9.06 18.57 predicted_1
SMAPE 36.78 45.01 predicted_1
MASE 0.20 0.24 predicted_1
R^2 0.96 0.97 predicted_2

※ RMSPE、MAPEはy=0のデータが含まれる場合に0除算となるため、除外して計算しています。

土日に伸びるモデルを選びたい場合は、RMSEのベースの誤差の二乗にペナルティが発生する指標の方が良かったりします。
（RMSPEでは実績の小さい値の時の誤差のペナルティが大きくなりすぎるので評価が逆転しています。）

今回使用しているデータは私が作成したデータですが実際のデータでも似たようなことが起こります。

さいごに

回帰モデルの代表的な評価指標についてまとめてみました。
データの特徴、予測する目的、わかりやすさなどを踏まえて良い指標を選ぶことができると良いと思います。

複数指標見て判断すると良いという結論は多いですが、認知負荷も増えるので個人的には1つに絞った方が良いと考えています。

どうしても良い指標がない場合は自分で作るのもおすすめです。

この記事が、みなさんの指標選びのヒントになれば幸いです。

参考

・回帰モデルの評価指標
https://qiita.com/DS27/items/2204b10888a19869e083

https://arxiv.org/pdf/1809.03006

・決定係数
https://bellcurve.jp/statistics/course/9706.html

Goals Tech Blog
Goals Tech BlogPublication

飲食業界向けSaas 「HANZO」シリーズを展開している株式会社Goalsのテックブログです。

Discussion