偏自己相関で周期をみつけよう

突然ですが、自分の興味のあるデータがどんな周期で変動しているか気になったことはありませんか？
私はあります(強気)。

この記事を読んでいる皆様方も、等しくこんな気持ちをお持ちなのを前提で、実データを例に時系列データの中に存在する周期を発見する手法を試そうと思います。

自己相関係数

時系列データに特有な統計量として、自分自身との相関を示す、自己相関係数と偏自己相関係数というものが存在します。まずは自己相関係数をみてみましょう。

自己相関係数（Autocorrelation Coefficient）

ここで$k$次の自己相関係数とは以下の様なものを指します。

$$\rho_{k} = Corr[y_t,y_{t-k}] = \frac{Cov[y_t,y_{t-k}]}{\sqrt{Var[y_t] \times Var[y_{t-k}]}}$$

• $Cov[y_t,y_{t-k}]$ : $t$と$t-k$時点間での共分散、k次の自己共分散
• $Var[y_t]$ : 時系列データの$t$時点での標準偏差
• $Var[y_{t-k}]$ : 時系列データの$t-k$時点での標準偏差

自己相関係数の意味

自己相関は同じデータ系列の中で時点$t$と過去の時点$t-k (k \geq 0)$との相関度合いを表す指標です。$\rho_{k}$が正の場合、時点$t$での変化は、$t-k$時点での変化と同じ方向を辿る可能性が高いと言えます。もちろん逆も然りです。

自己相関係数の可視化

自己相関係数には問題点があるのですが、それをみる前に、グラフにしてみましょう。
自己相関係数を次数順に並べたものを自己相関関数(コレログラム)といいます。これを可視化してみます。

このデータは東京電力さんのHPから取得させていただきました。

まずは簡単な下準備として、使用するライブラリのインポートと、時間単位データであったものを月次に集計し直しました。

import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# 数年分のデータを結合したものをjuyo_all.csvとして保存してあります
df = pd.read_csv('./juyo_all.csv')

# DATE列のキャストとMONTHカラムの追加
df['DATE'] = pd.to_datetime(df['DATE'])
df['MONTH'] = df['DATE'].dt.to_period('M')

# 月毎に集計
monthly_sum_kW = df.groupby('MONTH')['kW'].sum()

MONTH	kW
2016-04	2083676
2016-05	2111913
2016-06	2175670
2016-07	2465977
2016-08	2600249
...	...
2022-08	2674658
2022-09	2316185
2022-10	2104690
2022-11	2089663
2022-12	2538581

今回使うデータを一部プロットしたのが以下です。

自己相関関数のプロットはstatsmodelを使用して簡単に書けます。今回は次数30までを表示させてみました。acfはAutocorrelation Coefficient Functionの略です。

fig, ax = plt.subplots(figsize=(15, 6))  
sm.graphics.tsa.plot_acf(monthly_sum_kW,lags=30,ax=ax)
plt.show()

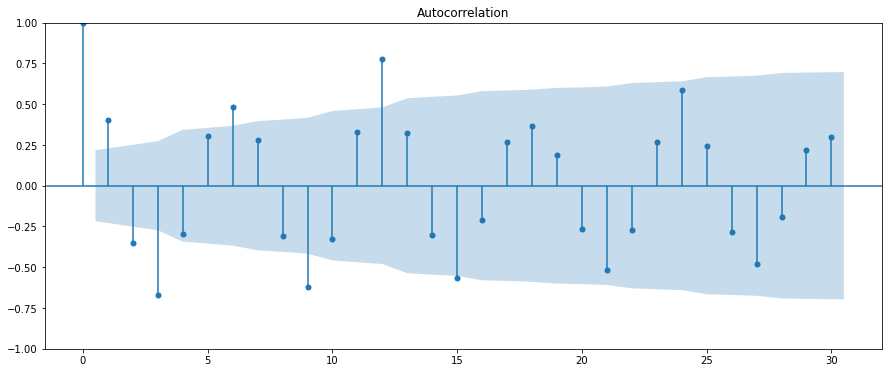
ここで青い領域は相関を持たない95%の信頼区間を示しています。
また、グラフをグッと睨むと以下が見えます

1. 次数0の場合が1
   次数0は同じ時点との相関なので1になります。
2. 1次以降は減衰振動している
   時点間の間隔が大きくなれば相関が弱くなっていることから、次数が大きくなれば減衰していきます。
3. いくつか信頼区間を外れて特に高い相関をもっていると示している次数がある
   次数が3の倍数である時に相関が大きくなっています。元のデータをみてみると、電力消費量は夏冬に高くなり、春秋に低くなることが見てとれます。よって相関が3ヶ月毎に高低を繰り返すのはその表れであると考えられます。

自己相関関数の問題点

自己相関関数を可視化しましたが、自己相関関数には推移則が存在します。推移則とは簡単にいうと、

$$A \rarr B \rarr C$$

のような関係がある時に、$A$と$C$の間にも

$$A \rarr C$$

のような関係も存在することを言います。
今回のデータの例では、$k \geq 0$に対して、$t-k-1$と$t-k-2$での相関があれば、以降もドミノ倒し的に相関が伝播していきます。これでは、ある異なる時点間の単純な相関関係を評価することは難しくなります。

偏自己相関係数

自己相関係数は、時系列データの過去の値と現在の値の間の相関、例えば時点$t$と時点$t−k$の間の相関を表します。
これには、時点$t$と時点$t-k$の間にある$k-1$個の自己相関係数が推移則によって伝播するため単純な時点間の相関を表していないという問題がありました。

一方、偏自己相関係数は、時点$t$と時点$t-k$の間にある時点の影響を取り除き、直接的な相関を測定します。これにより、前述の推移則の影響をうまく排除して、純粋な二点間の相関を扱うことができます。

偏自己相関係数(Partial Autocorrelation Coefficient)

ここで$k$次の偏自己相関$\phi_{kk}$は、$k$次の自己相関関数$\rho_{k}$を用いて以下の様に行列の形で書けます。

$$\begin{pmatrix} 1 & \rho_1 & \cdots & \rho_{k-1} \\ \rho_1 & 1 & \cdots & \rho_{k-2} \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{k-1} & \rho_{k-2} & \cdots & 1 \\ \end{pmatrix} \begin{pmatrix} \phi_{k1} \\ \phi_{k2} \\ \vdots \\ \phi_{kk} \\ \end{pmatrix} = \begin{pmatrix} \rho_1 \\ \rho_2 \\ \vdots \\ \rho_k \\ \end{pmatrix}$$

偏自己相関係数の可視化

今回も次数30までを表示させてみました。

fig, ax = plt.subplots(figsize=(15, 6))  
sm.graphics.tsa.plot_pacf(monthly_sum_kW,lags=30,ax=ax)
plt.show()

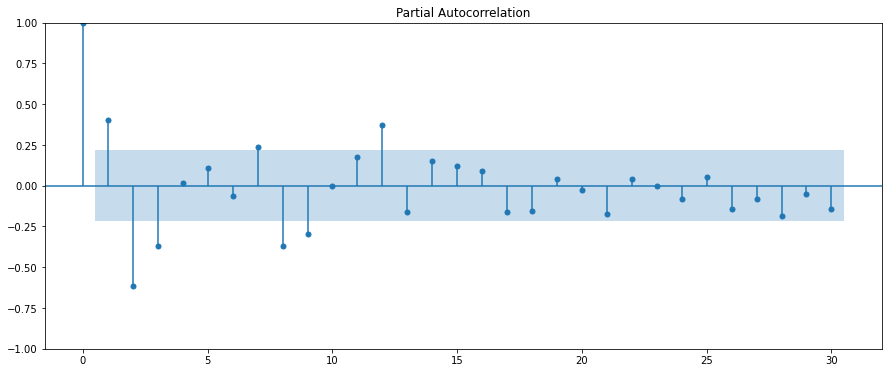
偏自己相関のグラフを睨みます。

自己相関の結果と比べて、広い時間間隔での値の絶対値が小さくなっていることがわかります。減衰振動するパターンもなくなりました。
また、次数2,3,8,9でそこそこな大きさの負の相関を持つことがわかります。これは例えば1月からの電力消費の変化を考えてみると、3,4,9,10月では電力消費が小さくなるため相関が負の方向に大きくなったものと考えられます。
他の値が自己相関関数と比べて小さくなったので、12ヶ月で周期を持ちそうだとわかります(本当に?)。

まとめ

なーんか、実際のデータに適用したら、自己相関関数の方が周期わかりやすくないです？と思ってしまいました...。データの特性にも依ってしまうのでしょうか？

自己相関、偏自己相関は時系列データそのものの周期を見つける他に、予測結果との残差に対して適用すると、回帰が正常におこなわれているかの検証にも使えたりします。これは今後試そうかなと。