季節調整をやってみる

季節調整

季節調整とは、時系列データで時折見られる、データが何かしらの周期をもって変動している場合に、それらをいくつかの要因毎に分けて取り扱う為に使われる手法です。
ここでは特に原系列データを以下の３つの系列

• トレンド成分
• 季節成分
• 残差成分

に分けることを指すことにします。
この記事は、実データに対して季節調整を通して遊んでみようというのが趣旨になります。

...成分？

それぞれの成分について以下で簡単に説明します。

トレンド成分

トレンド成分は、原系列データの長期的な変動や傾向を表します。データ値が上昇傾向であるとか、横ばいであるとか、それとも下降傾向があるのかといった長期的な性質を含みます。

季節成分

季節成分は、原系列が陰として持っている(ない場合はやっても効果は見込めません)周期性を表します。たとえば、今回扱う電力消費量であれば、年単位での周期性、週単位での周期性を表します。

残差成分

残差成分は、原系列から、トレンド成分と季節成分を除いた残りの部分であり、上記２成分で表せなかったものです。ノイズだったり、誤差が含まれることになります。

モチベーション

季節調整をやるモチベーションはいくつかありますが、上記の3成分からいくつかを取り出す(取り除く)だけでもデータ理解に繋がります。
例えば以下になります(ちなみに文字を書くのがめんどくさくなってきたので、以下の4項目はChatGPTに書いてもらいました)。

季節要因の除去

季節調整により、季節的な変動がデータから取り除かれます。これにより、需要パターンの本質的なトレンドや変動がより明確になります。季節的な影響を排除することで、需要予測モデルがより正確な予測を行うことが期待されます。

トレンドの把握

トレンド成分の分析は、将来の需要の長期的な傾向を理解するのに役立ちます。季節調整により、需要の増加や減少の本質的なパターンを把握することができます。これにより、需要の将来的な動向をより正確に予測することが可能になります。

ノイズの低減

季節調整により、ランダムなノイズや外れ値が含まれる可能性が低くなります。これにより、予測モデルがより安定した結果を生成しやすくなります。安定した予測結果は、需要予測において信頼性の高い意思決定を支援します。

予測精度の向上

季節調整により、需要予測モデルの精度が向上します。季節成分やトレンド成分が適切に把握されることで、将来の需要をより正確に予測することが可能になります。これにより、需要予測の誤差が減少し、生産計画や在庫管理などの重要なビジネス上の意思決定に対する信頼性が向上します。

実装例と結果

データは東京電力さんのこちらから取得できるものを使用させていただきました。
このデータは電力消費量が、日付、時間毎に記録されています。今回の記事では2016年から2022年までのデータを使うことにし、全ての年次データを結合したものをjuyo_all.csvとして保存してあります。

年を周期とした季節調整 ver1

電力需要って、比較的過ごしやすい春や秋では小さくなり、夏や秋では高くなるイメージがありますよね。ちなみに本当に周期的であるかは別途検証が必要ですが、ここでは目を瞑ることにします。
以下は必要なライブラリとデータの準備です。

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

df = pd.read_csv('juyo_all.csv')

	DATE	TIME	kW
0	2016/4/1	0:00	2555
1	2016/4/1	1:00	2433
2	2016/4/1	2:00	2393
3	2016/4/1	3:00	2375
4	2016/4/1	4:00	2390
...	...	...	...
59179	2022/12/31	19:00	3354
59180	2022/12/31	20:00	3293
59181	2022/12/31	21:00	3206
59182	2022/12/31	22:00	3092
59183	2022/12/31	23:00	3052

まずは、１年毎に365日×24時間のデータがあるので、ノイズなんて気にせず、潤沢にデータを使ってみましょう。周期を24×365=8760としてみます。

# 季節調整の実行
result = seasonal_decompose(df['kW'], model='additive', period=8760)

季節調整自体はとても簡単ですね。statsmodels便利！
ちなみに今回実施する可視化も簡単です。

# グラフのプロット
plt.figure(figsize=(22, 6))
plt.subplot(411)
plt.plot(df['DATE'], df['kW'], label='Original')
plt.legend(loc='upper left')
plt.subplot(412)
plt.plot(df['DATE'], result.trend, label='Trend')
plt.legend(loc='upper left')
plt.subplot(413)
plt.plot(df['DATE'], result.seasonal, label='Seasonal')
plt.legend(loc='upper left')
plt.subplot(414)
plt.plot(df['DATE'], result.resid, label='Residuals')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

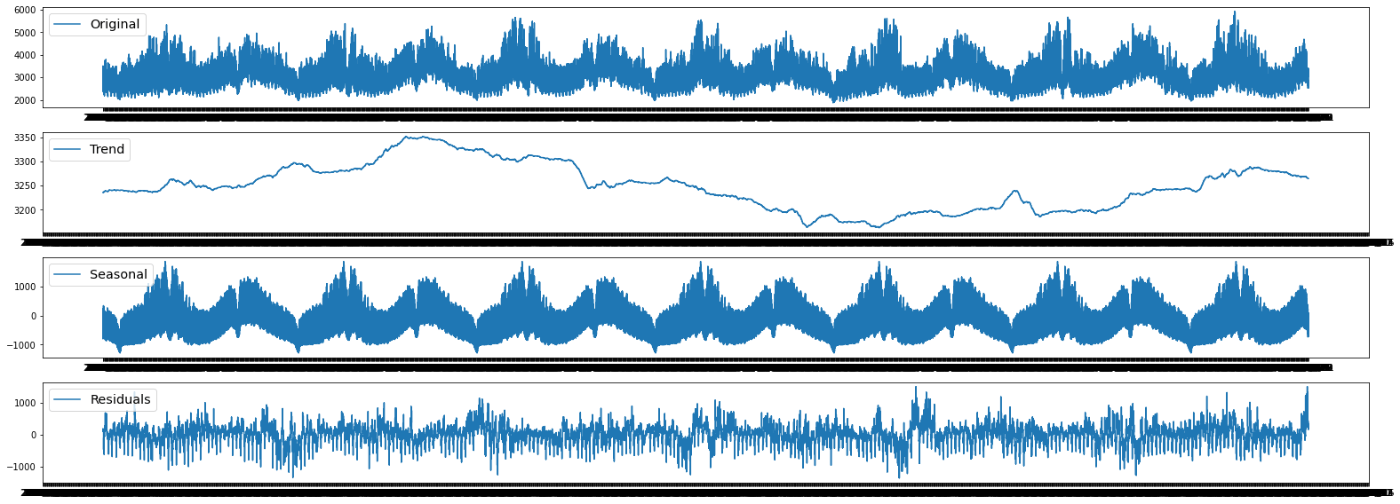
24時間×365日=8760を周期として季節調整を行いましたが、残差が原系列に対していささか割合として大きい様に思います。これは、データが細かすぎると、乗っているノイズも含めて最適化をおこなうために、トレンド成分と季節成分で表すことができない値が大きくなってしまうためだと思われます。

年を周期とした季節調整 ver2

では、次はノイズを低減し、適切な成分分解をおこなうために、月毎の平均をとり、さらに、周期を12ヶ月としてみます。

# データを読み込む
df = pd.read_csv('juyo_all.csv')

# 'DATE'列を日付型に変換して、月ごとの平均を計算する
df['DATE'] = pd.to_datetime(df['DATE'])
df_monthly_avg = df.resample('M', on='DATE').mean()

# 季節調整の実行
result = seasonal_decompose(df_monthly_avg['kW'], model='additive', period=12)

結果は以下です。

Trendの推移成分から、2018年の冬であたりで大きく、2020年の夏前で一度小さくなり、2022年の年末にかけて再度大きくなるトレンドがあったことがわかります。
また、Seasonalに目をやると、春秋で値が小さく、夏冬で値が大きくなる傾向があることがわかります。これは期待されたとおり、過ごしやすい季節ではエアコンなどの消費電力が比較的少なくなるからだと思われます。

週を周期とした季節調整

次は、年毎ではなく、週を周期として季節調整をおこなってみます。見立てでは曜日毎の消費電力のパターンを見つけられるのではないかと期待しています。

# データを読み込む
df = pd.read_csv('juyo_all.csv')

# 'DATE'列を日付型に変換して、日付ごとの平均を計算する
df['DATE'] = pd.to_datetime(df['DATE'])
df_daily_avg = df.resample('D', on='DATE').mean()

# 季節調整の実行
result = seasonal_decompose(df_daily_avg['kW'], model='additive', period=7) 

可視化結果は以下です。

Trendには、指定した周期(1週間)よりも大きい周期である、年単位周期での変度と、年を跨いだ増減傾向が含まれており、他方、Seasonalでは、曜日毎の変動パターンが表示されています。

Seasonalが細かすぎてちょっと見にくいので、拡大したものも載せておきます。

2016年4月1日は金曜日だったようです。グラフをみてみると、どうやら土曜日、日曜日での電力消費は、その他に比べて少ない傾向にあるようです。これは活動をおこなう企業や大学の施設等が、平日に割合として多いからではないかと推測しました。

まとめ

今回は電力消費量に対して季節調整を実行してみました。
自身で家の電気料金を払っている感覚では、平日より休日の方が在宅時間が長く、電気消費量も大きくなるのかな？と思っていたのですが、そこはむしろ全体からの割合としては小さかったのか、と改めて可視化することの大切さがわかった気がします。
今回実施しなかったのですが、24時間の電力消費パターンなども出すことができるな〜とか、思いました。
また、このトレンド成分、季節成分を元に未来の電力需要予測に繋げるにはどうするか、春夏秋冬などの季節毎に平均をとってはどうか、など、まだまだ手元で遊べそうなので、また今度気が向いたらやってみようと思います。