主成分分析(PCA)の実装_世界の統計
前書き
機械学習に関する仕事をしながら年に複数回旅行ができれば幸せな人生だと考えているAIエンジニアです。今年は初めて行く都市が多くてなかなか良い年です。人生の幕を閉じる前に行きたいところリストを制覇したいものです。仕事と旅行は計画的に!
今までの記事で
・主成分分析の哲学(考え方)と理論
・データの作成
をまとめました。
今回は実装部分をまとめていきたいと思います。
主成分分析の実装
処理の大きな流れ
主成分分析の理論の結果、分散共分散行列の固有ベクトルと固有値を利用して軸を新しく作ることで特徴的な部分を残しながら情報を削減できる事を学びました。
よってやるべき事をまとめると
・元のデータから分散共分散行列の作成
・分散共分散行列の固有ベクトル・固有値の計算
・固有ベクトルと固有値を利用した元データの変換
となります。
大きく分類するとこれだけですが、細かな部分で注意すべき点もあるので都度書いていきます。
主成分分析の考え方と理論はこちらのページにまとめてあります。
使用するデータ
まずは使用するデータについてです。
総務省統計局が提供してくださっている世界の統計のデータを利用しています。
出典:「世界の統計2024」(総務省統計局) (URL) (2024年7月25日に利用)
テーブルデータの作成はこちらの記事にまとめてあります。
よろしければご覧ください。
データの標準化(Z-score normalization)
まず今回"country"のカラムは使用しないので削除します。またfloat型に変換しておきます。
import os
import numpy as np
import pandas as pd
dir_path = "workspace_dir/input_data"
file_name = "20240725_for_pca.csv"
data_path = os.path.join(dir_path, file_name)
using_df = pd.read_csv(data_path, index_col=0)
pca_df = using_df.iloc[:, 1:]
pca_df = pca_df.astype("float64")
pca_df
| land_area | forest_area | forest_rate | artificial_forest_area | forest_area_diff | forest_area_diff_rate | num | estimated_num_2020 | estimated_num_2022 | birth_rate_2015 | birth_rate_2020 | death_rate_2015 | death_rate_2020 | gdp_2015 | gdp_2017 | gdp_2018 | gdp_2019 | gdp_2020 | gdp_2021 | life_expectancy | male_life_expectancy | female_life_expectancy | healthy_life_expectancy | male_healthy_life_expectancy | female_healthy_life_expectancy | population_density | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 364560 | 249350 | 68.4 | 101840 | -3.1 | -0 | 126146 | 1.26146e+08 | 124947 | 8 | 6.6 | 11 | 12.1 | 4.4454e+06 | 4.9313e+06 | 5.0425e+06 | 5.1179e+06 | 5.0483e+06 | 5.0037e+06 | 84 | 81 | 87 | 74 | 73 | 75 | 346.023 |
| 1 | 1.62876e+06 | 107520 | 6.6 | 10010 | 6 | 0.1 | 79926 | 8.729e+07 | 88551 | 19.4 | 14.2 | 4.8 | 5.6 | 417210 | 503710 | 526365 | 519356 | 543654 | 594892 | 77 | 76 | 79 | 66 | 66 | 67 | 53.5929 |
| 2 | 2.97319e+06 | 721600 | 24.3 | 132690 | 266.4 | 0.4 | 1.21086e+06 | 1.39639e+09 | 1.41717e+06 | 18.8 | 16.6 | 6.7 | 7.4 | 2.14676e+06 | 2.62433e+06 | 2.7632e+06 | 2.85073e+06 | 2.6722e+06 | 3.20147e+06 | 71 | 70 | 72 | 60 | 60 | 60 | 469.66 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 31 | 263310 | 98930 | 37.6 | 20840 | 4.4 | 0.1 | 4793 | 5.061e+06 | 5185 | 13.1 | 12.5 | 6.6 | 6.4 | 178064 | 206624 | 211953 | 213435 | 212214 | 250451 | 82 | 80 | 84 | 70 | 70 | 71 | 19.2207 |
当たり前ですが、作成したデータは列毎に様々なデータが入っていて単位もスケール(値の大きさやバラツキの大きさ)もバラバラな状態です。
このような時、それぞれの値を列毎の平均が0, 標準偏差が1になるような値(Z値)に変換することで単位やスケールの違いを気にせずに済むようになります。
※この変換はZ-score normalizationとか標準化(Standardization)とかよばれます。
(広い意味でのデータの正規化です。)
数式で書くと
このような計算をします。
以下のコードでZ値に変換後の行列を作成できます。
def generate_z_score_matrix(matrix):
"""Z値の行列を作成する"""
column_mean = np.mean(matrix, axis=0)
print("mean")
print(column_mean)
column_std = np.std(matrix, axis=0, ddof=1)
print()
print("std")
print(column_std)
z_score_matrix = ( (matrix - column_mean) / column_std)
print()
print("Z_mean")
print(np.mean(Z, axis=0))
print()
print("Z_std")
print(np.std(Z, axis=0, ddof=1))
return z_score_matrix
z_score_matrix = generate_z_score_matrix(pca_df.values)

元の平均と標準偏差はバラバラなのに対し、z値に変換後の平均(Z_mean)と標準偏差(Z_std)は0と1になっていることが確認できます。
(平均(Z_mean)は数値計算の誤差の関係で0ちょうどにはなっていませんが、10のマイナス17乗とかの値になっているのでほとんど0です。ちっちゃいことは気にするな♪)
分散共分散行列の作成
次に分散共分散行列を計算していきます。
列毎の平均(Z値に変換した場合は0)を引いた行列の転置行列と転置前の行列の積を計算しデータ数で割ることで計算できます。
def generate_cov_matrix(matrix):
"""
分散共分散行列を作成する
行列の積ではデータ数(不偏標準偏差を利用した場合はデータ数 - 1)倍された値になるのでそれぞれの要素をデータ数で割る
"""
data_num = matrix.shape[0] - 1
means = np.mean(matrix, axis=0)
diff_mean = matrix - means
cov_sum = (diff_mean.T @ diff_mean)
cov_matrix = cov_sum / data_num
return cov_matrix
cov_matrix = generate_cov_matrix(z_score_matrix)
pd.DataFrame(cov_matrix)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0.932203 | 0.0757723 | 0.569541 | 0.14188 | 0.0911632 | 0.32008 | 0.296979 | 0.293587 | -0.148606 | -0.186378 | 0.147459 | 0.187319 | 0.444149 | 0.449921 | 0.449978 | 0.45003 | 0.44336 | 0.456989 | 0.0284587 | -0.0265941 | 0.0591371 | 0.00362972 | -0.0394569 | 0.0555815 | -0.314272 |
| 1 | 0.932203 | 1 | 0.27893 | 0.404345 | -0.117657 | 0.010283 | 0.165383 | 0.148769 | 0.146134 | -0.145854 | -0.173204 | 0.234691 | 0.289318 | 0.292974 | 0.297275 | 0.292289 | 0.292896 | 0.280096 | 0.286114 | -0.00654636 | -0.0831449 | 0.041622 | -0.0234347 | -0.0788388 | 0.0469483 | -0.277443 |
| 2 | 0.0757723 | 0.27893 | 1 | 0.058358 | -0.32963 | 0.0445849 | -0.13779 | -0.144617 | -0.14722 | -0.359105 | -0.335283 | 0.199773 | 0.270019 | 0.0461734 | 0.0476542 | 0.0404982 | 0.038841 | 0.0304043 | 0.0156736 | 0.346861 | 0.288351 | 0.386606 | 0.389166 | 0.340133 | 0.421597 | -0.093562 |
| 3 | 0.569541 | 0.404345 | 0.058358 | 1 | 0.644057 | 0.386283 | 0.762824 | 0.717163 | 0.711146 | -0.252727 | -0.288894 | 0.0272426 | 0.0510501 | 0.680075 | 0.69382 | 0.715067 | 0.712884 | 0.724514 | 0.75398 | 0.128878 | 0.121591 | 0.139978 | 0.167382 | 0.139716 | 0.166551 | -0.0955482 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| 25 | -0.314272 | -0.277443 | -0.093562 | -0.0955482 | 0.110673 | 0.135335 | 0.175742 | 0.179497 | 0.181717 | -0.00831322 | 0.00106182 | -0.162259 | -0.216104 | -0.0791432 | -0.0737726 | -0.0705042 | -0.0695425 | -0.0648732 | -0.0681703 | -0.0735503 | -0.0411716 | -0.0885003 | -0.0588345 | -0.0366955 | -0.0907202 | 1 |
実対象行列(要素が全て実数で転置しても元の行列と一致する行列)になっていることを確認できます。
ちなみにZ値に変換したデータの分散共分散行列は相関係数行列と一致します。
(相関係数は共分散をそれぞれの項目の標準偏差で割って正規化したものですが、Z値に変換すると標準偏差が1になり分母が1になるためです。)
参考までにnpの関数との差です。
diff_frobenius_norm_np_cov = ((cov_matrix - np.cov(z_score_matrix, y=None, rowvar=False)) ** 2).sum()
print("npの分散共分散行列との差: ", diff_frobenius_norm_np_cov)
# npの分散共分散行列との差: 8.640941423459553e-31
diff_frobenius_norm_np_corrcoef = ((cov_matrix - np.corrcoef(z_score_matrix, y=None, rowvar=False)) ** 2).sum()
print("npの相関係数行列との差: ", diff_frobenius_norm_np_corrcoef)
# npの相関係数行列との差: 5.1418643223629736e-30
↑差がほとんど0になっていることが確認できます。
固有ベクトル・固有値の計算
次に固有ベクトル・固有値を計算していきます。
npのlinalg.eigを使うことで計算できます。
e_values, e_vector_matrix = np.linalg.eig(cov_matrix)
print("固有値")
print(e_values.shape)
# (26,)
print("固有ベクトル")
print(e_vector_matrix.shape)
# (26, 26)
結果の確認
固有値と寄与率の結果
具体的に中身を見ていきます。
先に固有値を見ていきます。
分散共分散行列の固有値は分散を意味します。
全部の分散のうち合成後のそれぞれの軸が占めている分散の割合(寄与率)とその累積値(累積寄与率)を計算してまとめてみます。
def generate_evalue_info_df(e_values):
""""固有値, 寄与率, 累積寄与率をまとめたdfを作成"""
e_value_sum = e_values.sum()
# 寄与率の計算
contribution_ratio = e_values / e_value_sum
# 累積寄与率の計算
cumulative_contribution_ratio = np.cumsum(contribution_ratio)
# 固有値、寄与率、累積寄与率をまとめる
e_value_info = np.concatenate([[e_values], [contribution_ratio], [cumulative_contribution_ratio]], 0)
index = ["固有値", "寄与率", "累積寄与率"]
columns = ["p" + str(index+1) for index in range(len(e_values))]
e_value_info_df = pd.DataFrame(e_value_info, index=index, columns=columns)
return e_value_info_df
e_value_info_df = generate_evalue_info_df(e_values)
e_value_info_df
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | p11 | p12 | p13 | p14 | p15 | p16 | p17 | p18 | p19 | p20 | p21 | p22 | p23 | p24 | p25 | p26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 固有値 | 9.85899 | 6.96661 | 2.98104 | 1.73924 | 1.42611 | 1.01462 | 0.736971 | 0.4863 | 0.370923 | 0.22565 | 0.0904013 | 0.0439865 | 0.0279827 | 0.013453 | 0.00783747 | 0.00434769 | 0.00225093 | 0.00155896 | 0.000803999 | 0.000641084 | 0.000158056 | 6.85892e-05 | 4.01978e-05 | 1.12018e-05 | 1.0105e-06 | 5.46367e-06 |
| 寄与率 | 0.379192 | 0.267947 | 0.114655 | 0.0668937 | 0.0548506 | 0.0390238 | 0.028345 | 0.0187039 | 0.0142663 | 0.00867883 | 0.00347697 | 0.00169179 | 0.00107626 | 0.000517423 | 0.000301441 | 0.000167219 | 8.65741e-05 | 5.99601e-05 | 3.0923e-05 | 2.46571e-05 | 6.07908e-06 | 2.63804e-06 | 1.54607e-06 | 4.30838e-07 | 3.88656e-08 | 2.10141e-07 |
| 累積寄与率 | 0.379192 | 0.647138 | 0.761794 | 0.828687 | 0.883538 | 0.922562 | 0.950907 | 0.969611 | 0.983877 | 0.992556 | 0.996033 | 0.997725 | 0.998801 | 0.999318 | 0.99962 | 0.999787 | 0.999874 | 0.999933 | 0.999964 | 0.999989 | 0.999995 | 0.999998 | 0.999999 | 1 | 1 | 1 |
↑累積寄与率の結果から第一主成分(p1)だけで全体の分散の約38%, 第一主成分(p1)と第二主成分(p2)の2軸で約65%、同様に第三主成分(p3)までの3軸で約76%を表現できることが分かります。
また寄与率の結果から第四主成分(p4)以降は全体の分散の約10%以下であることがわかります。
累積寄与率の結果を折れ線グラフで見てみます。
e_value_info_df.T.plot.line(y=["累積寄与率"], ylim=(0, 1), marker="o")

↑グラフからも第一主成分(p1)で40%弱、第一主成分(p1)と第二主成分(p2)の2軸で60%強の分散を表現できていることがわかります。また、第十一主成分(p11)以降の軸はほとんど影響しないことも分かります。
次元を削減する時の基準は様々ありますが、今回は全体の70%以上を表現できているという基準で次元を3つに削減することにします。
固有ベクトルの結果と軸の解釈
次に固有ベクトルの結果を見ていきます。
累積寄与率の結果から次元を3つに絞ることにしたので、第三主成分(p3)までの結果を確認します。
def generate_e_vector_df(e_vector_matrix, pca_df_columns, num_of_dimension=None):
"""固有ベクトルをまとめたdfを作成する"""
columns = ["p" + str(index+1) for index in range(e_vector_matrix.shape[0])]
if num_of_dimension:
columns = columns[:num_of_dimension]
e_vector_matrix = e_vector_matrix[:, :num_of_dimension]
e_vector_df = pd.DataFrame(e_vector_matrix, index=pca_df_columns, columns=columns)
return e_vector_df
e_vector_df = generate_e_vector_df(e_vector_matrix, pca_df.columns, num_of_dimension=3)
e_vector_df
| p1 | p2 | p3 | |
|---|---|---|---|
| land_area | 0.133638 | 0.13902 | -0.253528 |
| forest_area | 0.0894894 | 0.0948706 | -0.335279 |
| forest_rate | 0.0724927 | -0.128071 | -0.238961 |
| artificial_forest_area | 0.2281 | 0.18997 | 0.0363571 |
| forest_area_diff | 0.186578 | 0.0717666 | 0.271166 |
| forest_area_diff_rate | 0.191038 | -0.06318 | 0.219826 |
| num | 0.147522 | 0.249341 | 0.23795 |
| estimated_num_2020 | 0.130906 | 0.255045 | 0.237969 |
| estimated_num_2022 | 0.128582 | 0.256051 | 0.238496 |
| birth_rate_2015 | -0.236983 | 0.210662 | -0.0105548 |
| birth_rate_2020 | -0.242097 | 0.199203 | -0.0225353 |
| death_rate_2015 | -0.00961641 | 0.0398703 | -0.400759 |
| death_rate_2020 | 0.0387575 | 0.000478852 | -0.415786 |
| gdp_2015 | 0.252479 | 0.177535 | -0.107411 |
| gdp_2017 | 0.254531 | 0.179619 | -0.100807 |
| gdp_2018 | 0.256215 | 0.1829 | -0.0911535 |
| gdp_2019 | 0.254451 | 0.185363 | -0.0914418 |
| gdp_2020 | 0.255112 | 0.186521 | -0.0822235 |
| gdp_2021 | 0.256547 | 0.192383 | -0.0688899 |
| life_expectancy | 0.222152 | -0.264555 | 0.0186876 |
| male_life_expectancy | 0.214872 | -0.258519 | 0.0601743 |
| female_life_expectancy | 0.221881 | -0.268635 | -0.00482029 |
| healthy_life_expectancy | 0.218476 | -0.269892 | 0.027524 |
| male_healthy_life_expectancy | 0.211332 | -0.268387 | 0.0488378 |
| female_healthy_life_expectancy | 0.215371 | -0.272372 | -0.00439609 |
| population_density | -0.0197248 | 0.0129451 | 0.285948 |
固有ベクトルは元の軸の重みを意味します。
具体的に、第一主成分(p1)では、陸地の面積(land_area)を約0.13倍, 森林の面積(forest_area)を約0.09倍, ..., 人口密度(population_density)を約-0.02倍していることになります。
しかし、軸(主成分)の説明をする時に"この軸は陸地の面積(land_area)を約0.13倍, 森林の面積(forest_area)を約0.09倍, ..., 人口密度(population_density)を約-0.02倍した軸"ですと言われてもどんな軸なのか理解しにくいと思います。
それぞれの軸(主成分)が"何を意味しているのか"は分析者が考える必要があります。
重みの関係を見ながら軸の意味を考えていきます。
元の軸の絶対値が大きな要素ほどその主成分に大きな影響を与えていることになるのですが、数値だけだと少し分かりにくいと思います。
一度ヒートマップで可視化した結果も見ながらそれぞれの主成分の意味を考えていきます。
import seaborn as sns
import matplotlib.pyplot as plt
def print_heat_map(df, vmax=1, vmin=0, center=0.5, cmap='Blues'):
"""
ヒートマップを作成する
デフォルトで最大1, 最小0, 中心0.5で作成
(デフォルトでは確率の結果を表示することを想定)
"""
vertical = len(df) / 4
fig = plt.figure(figsize=(7, vertical))
ax = sns.heatmap(df, xticklabels=1, yticklabels=1, vmax=vmax, vmin=vmin, center=center, linewidths=0.5, linecolor="Black", cmap=cmap)
ax.tick_params(labelsize=9)
plt.show()
plt.close()
return
def print_e_vector_heat_map(e_vector_df):
"""
固有ベクトルごとにヒートマップを作成する
中心を0にして絶対値の最大値で色のスケールを調整
プラスは赤、マイナスが青となる表示とする
"""
for column in e_vector_df:
print(column)
v_max = e_vector_df[column].abs().max()
v_min = (-1) * v_max
print_heat_map(pd.DataFrame(e_vector_df[column]), vmax=v_max, vmin=v_min, center=0, cmap="bwr")
return
print_e_vector_heat_map(e_vector_df)
まず、p1(第一主成分)の結果の結果を見てみます。
p1

このヒートマップはプラスに大きいほど赤色が濃く、マイナスに大きいほど青色が濃くなるように作成しています。
赤や青の色が濃い要素ほど、p1(第一主成分)の結果にも大きな影響を及ぼしています。
具体的に見ていくと、gdp, 平均寿命(life_expectancy), 健康寿命(healthy_life_expectancy)は赤色が濃く、これらの値が大きいほどp1(第一主成分)の値も大きくなることを表します。
逆に出生率(birth_rate)は青色が濃くなっているので、出生率の値が小さいほどp1(第一主成分)の値が大きくなることを表します。
まとめるとp1(第一主成分)の値が大きいということは、gdpが大きく寿命も長いが、出生率が小さくなっていることを意味します。
直感的に、経済が発展しきった先進国を彷彿させる軸となっています。
ここでは"現状の経済力の高さ"と解釈することにします。
同様にp2(第二主成分)の結果を見てみます。
p2
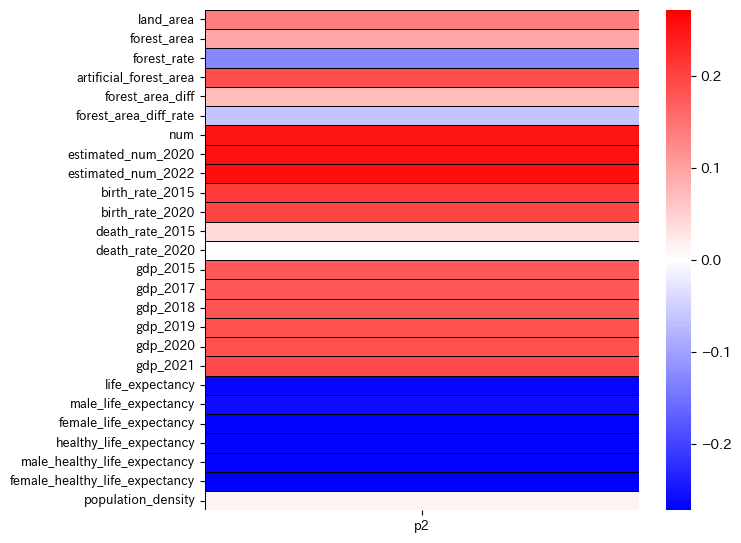
この図から
p2(第二主成分)が大きいということは、人口(num)が多く出生率も高いが、寿命が短いことを意味します。
人口増加中の途上国を彷彿させる軸となっています。
ここでは"今後の経済発展力の高さ"と解釈することにします。
p3
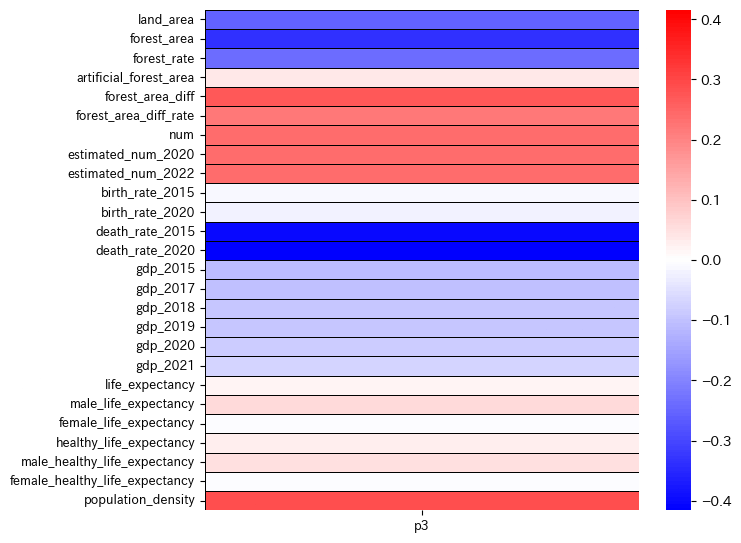
p3(第三主成分)が大きくなるほど、死亡率(death_rate)が低く, 森の面積(forest_area)も狭くて人口密度(population_density)が高いということが読み取れます。
解釈が難しいですが、領土に対して人の数が多く死亡率も低いという理由でここでは"人口増加のしやすさ"と解釈することにします。
固有ベクトルと固有値を利用した元データの変換
固有ベクトルと固有値が求まっているので元データを変換します。
変換後のデータを主成分得点(Principal component score)と呼びます。
def compute_principal_component_score_matrix(data, e_values, e_vector_matrix, num_of_dimension=None):
"""主成分得点を計算する"""
new_e_values = np.zeros_like(e_values)
new_e_values[:num_of_dimension] = e_values[:num_of_dimension]
ramda_matrix = np.diag(new_e_values)
principal_component_score_matrix = data @ e_vector_matrix @ ramda_matrix
return principal_component_score_matrix
principal_component_score_matrix = compute_principal_component_score_matrix(z_score_matrix, e_values, e_vector_matrix, num_of_dimension=3)
print(principal_component_score_matrix.shape) # (32, 26)
散布図の確認
主成分得点の結果を散布図で確認して見ます。まず散布図を作成するために便利なライブラリを使える状態にします。
# matplotlib日本語表示のインストール
!pip install japanize-matplotlib
# 散布図でテキストが重ならないようにするライブラリのインストール
!pip install adjustText
from adjustText import adjust_text
import japanize_matplotlib
japanize_matplotlib.japanize()
エラーが出なければOKです。
これでグラフ上に日本語が表示できるようになり、散布図上でテキストが被らないようにできます。
それでは実際に散布図を作成していきます。
絞った主成分のそれぞれの組み合わせで散布図を作成する仕様にしています。
import itertools
def print_sccater_plot_from_np_array(data, x_index, y_index, labels=None, data_names=None):
"""散布図を描画"""
x = data[:, x_index]
y = data[:, y_index]
fig = plt.figure(figsize=(7, 5)) # Figureオブジェクトを作成
ax = fig.add_subplot(1,1,1)
ax.scatter(x, y)
if labels is not None:
ax.set_xlabel(labels[0])
ax.set_ylabel(labels[1])
if data_names is not None:
texts = []
for i, data_name in enumerate(data_names):
texts.append(ax.text(x[i], y[i], data_name, fontsize=8))
adjust_text(texts)
plt.show()
plt.close()
return
def print_pca_result_sccater_plot(data, data_names, vector_name_dict):
vecror_names = list(vector_name_dict.values())
for labels in itertools.combinations(vecror_names, 2):
print(labels)
x_index = vecror_names.index(labels[0])
y_index = vecror_names.index(labels[1])
print_sccater_plot_from_np_array(data, x_index, y_index, labels=labels, data_names=data_names)
return
vector_name_dict = {
"p1": "p1_現状の経済力の高さ",
"p2": "p2_今後の発展力の高さ",
"p3": "p3_人口増加のしやすさ",
}
data_names = list(using_df.iloc[:, 0])
print_pca_result_sccater_plot(principal_component_score_matrix, data_names, vector_name_dict)
結果を見ていきます。
p1とp2の組み合わせ
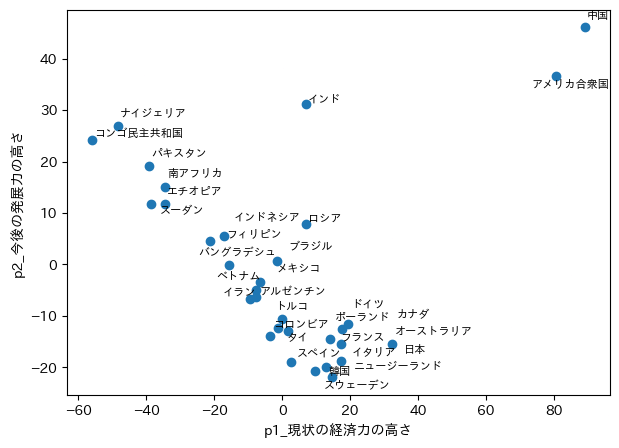
解釈が正しければ右上にいればいるほど、
現状の経済力が高く、今後の発展力も見込めることになります。
アメリカや中国の強さがデータからも見えてくると思います。
日本も現状の経済力は3番目にいることが分かります。
アフリカ諸国が左上に多いことからも、アフリカ諸国の今後の発展が期待できそうです。
p1とp3の組み合わせ
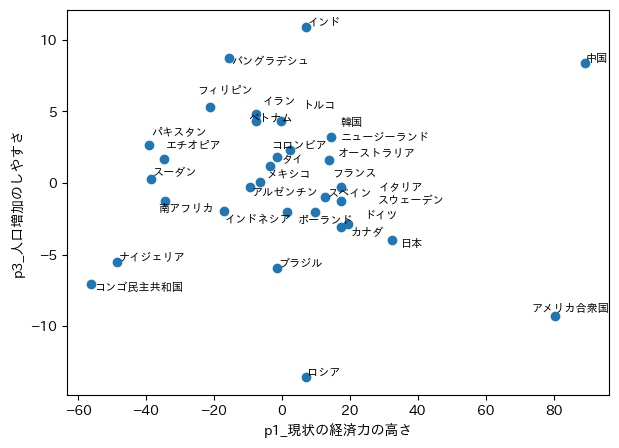
p3ではアジア系の国が上に多く、今後も人口が増加していきそうなことが分かります。
p2とp3の組み合わせ

中国、インドは今後の発展も人口増加も期待できそうです。
最も気になる日本は、、、
不愉快なことを言うな。
と言われそうですが、
現実はもっと不愉快です!!
といった状況です。
挽回していきたいものです。
まとめ
基本的な数学の説明から、主成分分析の理論、データの取得と整形、実装までまとめました。
何かと便利な分析手法でおすすめです。
どなたかの参考になれば幸いです。
感想ですが、生データの分析はどんな結果になるか分からないので面白いです。
参考
正規化と標準化
固有値・固有ベクトルの計算
主成分分析の軸の数の判断
ヒートマップ
matplitlibの日本語表示
散布図で重なる文字の対策
itertools
Discussion