多重共線性、相関から見るか？VIFから見るか？

これはなに？

先日、多重共線性の除去手法についての記事を書きました。因みにこれです。
https://zenn.dev/goals_techblog/articles/3fe8c2f63c23e6
この記事では、多重共線性に対処する方法として、以下を挙げました。

• 相関係数から変数を消去する
• VIFから変数を消去する
• 主成分分析
• Ridge回帰

これを見たときに『変数を消去するって二つあるけど、どっちがいいんですか？』ってなりませんか。書いておいてなんですが、私はなります。
結果としては多変量解析なのであれば、二変数間の関係しかみない相関係数ではなく、VIFを使わないと本当に多重共線性が発生しているかはわからないかもよ。というのが結論になりました。

今回は数式を少なくして、どのような違いがあるのかを簡単な数値実験を通して見てみます。

実験1 - 二変数間の多重共線性

二変数では単に共線性というのですが、以下のように、ある変数が、別の変数と相関が高い場合はどうなるでしょうか。

$$\begin{align} &\begin{split} Y = β_0+β_1X_1+β_2X_2+β_3X_3+\epsilon \end{split}\\ &\begin{split} X_1 = 5 \times N(0,1) \end{split}\\ &\begin{split} X_2 = X_1 + N(0,2) \end{split}\\ &\begin{split} X_3 = 5 \times N(0,1) \end{split} \end{align}$$

まずはライブラリをインポートして、データを作成します。

import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(0)
n = 200

# 変数を作成
X1 = 5 * np.random.normal(0, 1, n)
X2 = X1 + np.random.normal(0, 2, n)
X3 = 5 * np.random.normal(0, 1, n)

df = pd.DataFrame({'X1': X1, 'X2': X2, 'X3': X3})
X = df[['X1', 'X2', 'X3']]

この変数に対して、相関行列とVIFを計算してみます。

# 相関行列をプロット
correlation_matrix = df.corr()
sns.heatmap(correlation_matrix,annot=True)
plt.show()

# VIFを計算
X_with_const = sm.add_constant(X)
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X_with_const.values, i + 1) for i in range(len(X.columns))]

計算された相関行列を可視化したのが以下です。もちろん変数$X_1, X_2$の相関が高くなっているのがみてとれます。

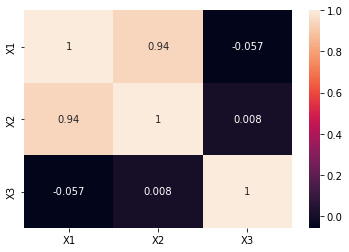
相関行列をプロットした例、$X_1, X_2$の相関係数がとても大きい

また、VIFの計算結果が以下となりました。$X_1, X_2$のVIF値が高くなっており、VIFから見た際にも$X_1,X_2$のどちらかを消す必要がありそうだとわかります。

feature	VIF
X1	9.124697
X2	9.095434
X3	1.038335

実験2 - 三変数間の多重共線性

次に複数の変数に相関をもつ変数が存在しているときどうなるかを試してみます。
以下のような変数を作成しました。この例では、$X_4$は$X_1, X_3$の二つの変数に相関を持っています。

$$\begin{align} &\begin{split} Y = β_0+β_1X_1+β_2X_2+β_3X_3+β_4X_4+\epsilon \end{split}\\ &\begin{split} X_1 = 5 \times N(0,1) \end{split}\\ &\begin{split} X_2 = N(0,2) \end{split}\\ &\begin{split} X_3 = 5 \times N(0,1) \end{split}\\ &\begin{split} X_4 = X_1 + X_3 + N(0,2) \end{split} \end{align}$$

流れとしては先ほどと同じなので、以下のようにまとめて実行しちゃいます。

X1 = 5 * np.random.normal(0, 1, n)
X2 = np.random.normal(0, 2, n)
X3 = 5 * np.random.normal(0, 1, n)
X4 = X1 + X3 + np.random.normal(0, 2, n)  

df = pd.DataFrame({'X1': X1, 'X2': X2, 'X3': X3, 'X4': X4})

X = df[['X1', 'X2', 'X3', 'X4']]

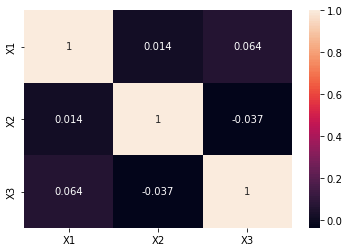
# 相関行列を計算
correlation_matrix = X.corr()
sns.heatmap(correlation_matrix,annot=True)
plt.show()

# VIFを計算
X_with_const = sm.add_constant(X)
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X_with_const.values, i + 1) for i in range(len(X.columns))]

結果はそれぞれ以下のようになりました。

相関係数では$X_4$と$X_1$、$X_4$と$X_3$の相関が高くなっていますが、これは多重共線性が発生しているのでしょうか？また、発生しているのならば、どれを消すことで多重共線性を解消できるのでしょうか。複数の変数との相関を持つ変数がある場合には相関係数のみではこのように判断つかないことが多いです。

$X_4$と$X_1,X_3$の相関が高くなっているが...？

VIFの計算結果は以下のようになりました。VIFは対象の変数に対して、それ以外全ての変数からどれだけ情報を再現できるかを計算するため、$X_1,X_3$から殆どを再現できる$X_4$のVIFの値が特に大きくなっています。

feature	VIF
X1	7.410399
X2	1.012492
X3	7.099382
X4	14.917272

$X_4$のVIFが高いので、消して再度相関係数とVIFを計算します。相関もVIFも小さくなっていて変数の治安が良さそうです。

feature	VIF
X1	1.004385
X2	1.001672
X3	1.005572

まとめ

• 相関係数は、単純に2つの変数間の線形関係を確認するのに便利です。計算も軽量なので、初期の探索段階で試す価値がありますが、多変量解析には不十分。
• VIFは、複数の変数が絡み合う場合に多重共線性をより効果的に評価できる指標です。特に、説明変数が多い回帰モデルでは、VIFを使って全体の変数関係を評価することが推奨されます。

実務では、まず相関係数でざっくりと変数間の関係を見た後、より正確な評価が必要な場合にVIFを使用するのが良いんじゃないかなと思います。