RECRUIT 日本橋ハーフマラソン 2022夏(AtCoder Heuristic Contest 013) 4位の貪欲解法+参加記
はじめに
AtCoderの長期ヒューリスティックコンテストである「RECRUIT 日本橋ハーフマラソン 2022夏(AtCoder Heuristic Contest 013)」に参加し、 システムテスト15,400,296点で4位を取りました。私の中ではかつてないほど良い順位だったので、記念として解法として採用した貪欲法の説明と、参加記を残します。
最終的な解のビジュアライズ結果(seed=2)
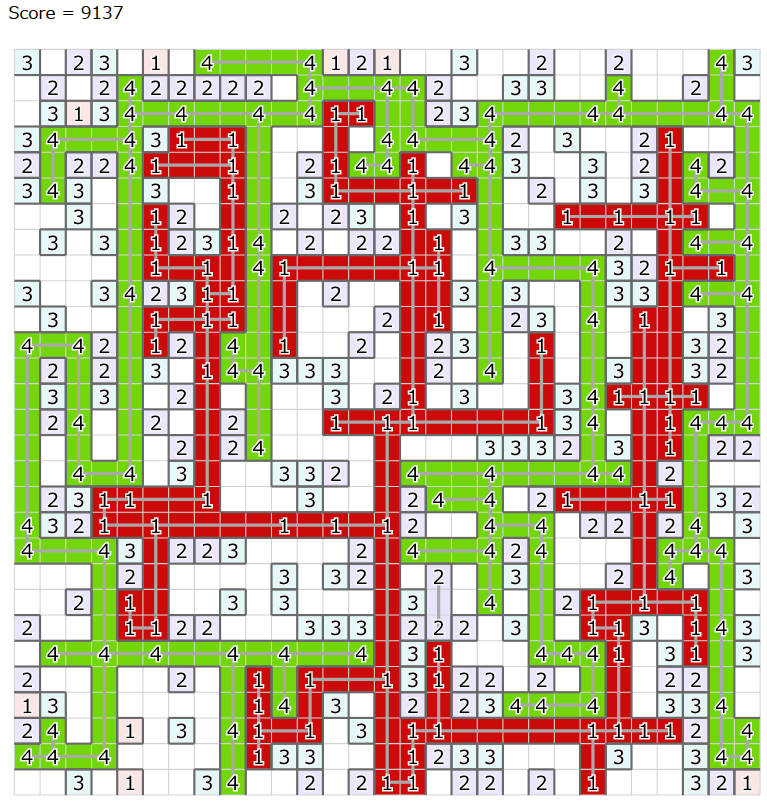
問題概要
AtCoder上の問題ページ参照
なお、この記事ではコンピュータの種類を「色」と呼ぶことにします。
解法
基本方針
異なる色の大きいクラスタを2個作ることを目指す。ただし密な盤面では1つ作ることを目指す場合もある。
クラスタ内には1色のみ含み、異なる色のコンピュータをつなぐことはない。
最初から最後まで行う貪欲を、初期値を乱択しながら時間いっぱい繰り返す。手元の環境では 100~1000回繰り返しできた。
貪欲の概要
貪欲の初期値として、クラスタの初期値を1点または、異なる色の2点を乱択により選ぶ。
毎回、既存のクラスタと同色のコンピュータのうち、クラスタに属していないものを移動させて、クラスタ内コンピュータへ接続する(クラスタへ取り込む)ことで、クラスタを拡張する。
取り込み操作は、多始点ダイクストラ+BFSにより行う。詳細は後述
初期値として2色選んだ場合は、おおよそ交互に取り込み操作を行う。他方の色が拡大しすぎるのを妨害しつつ自分の色を広げる、陣取りゲームのような動きに見える。
1個のコンピュータをクラスタに取り込む操作を、取り込み不可能になるまで繰り返す。取り込み不可能になった場合、次のクラスタ初期値を選んで再度貪欲を行う。
操作回数の上限に達したら終了。
多始点ダイクストラ+BFSによるクラスタへの取り込み
青とオレンジの2種類のコンピュータがあるとする。
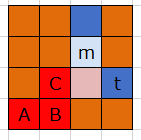
以下の図において、sの書いてある青いコンピュータから、他の青いコンピュータを取り込みたいとする。
まずはコンピュータsから、縦横の直線上に初期コストを割り当てる。空白マスを通るときはコスト追加は0だが、異なる色のコンピュータを通るときは固定のコスト10を追加して累積値を初期コストにする[1] [2]。
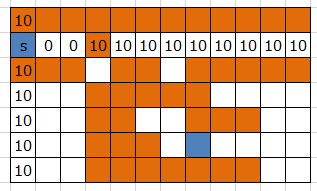
続いて、初期コストが割り当てられた場所を始点とする多始点ダイクストラを行う。
一歩移動するごとにコスト+1, 異なる色のコンピュータを通るときは追加で+10 する[3]。
コスト最小の青いコンピュータ (図中の25)を取り込み対象とする。
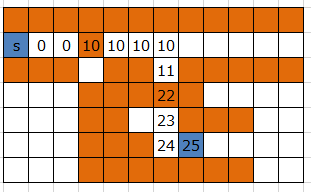
ダイクストラの復元を行って、取り込み対象コンピュータの移動経路(t->m)を求める。さらに、取り込み対象のコンピュータの目的地と、元のクラスタ内コンピュータの間の経路(s<->m)も求める。この2種類の経路上にあるセルを「予約済み」として扱う。 t->mに移動させ、s-mに線を引くことを目指す。
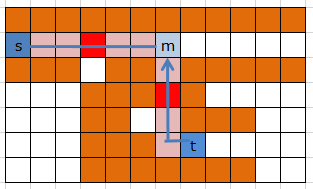
予約済みのセルにあるオレンジのコンピュータを「邪魔なコンピュータ」とみなす。
邪魔なコンピュータを、BFSにより予約済みでない空白マスに退避させる。
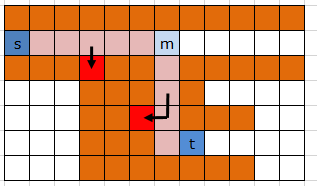
これで t->m に移動させ、 s-mの線を引くことが可能になる。tにあったコンピュータが、sの属するクラスタに取り込まれた形である。
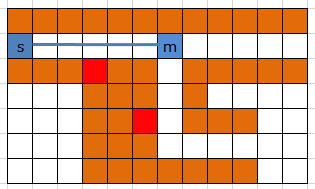
このダイクストラにおいて、他色コンピュータのコストは、邪魔なコンピュータを退避させるときにかかる手数を先取りしたものとして考えている。説明図では「移動コスト:他色コンピュータのコスト」を「1:10」にしていたが、提出コードでは「10:14」にするのが良かった。おそらく、退避に平均1.4手程度かかっていると思われる。
(追記) 取り込み元のクラスタ内に線で結ばれた複数のコンピュータがある場合
初期コストは、取り込み元クラスタの各コンピュータから伸ばすようにする。さらに、コンピュータ同士を結ぶ線上にも初期コスト0を割り当てる。線上のセルが取り込み対象のコンピュータの目的地になった場合、元あった1本の線を2本に分割して、取り込まれたコンピュータを挟むようにする。
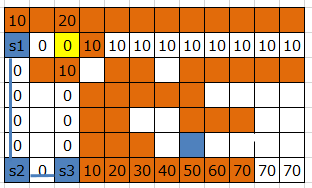
なお、初期コスト割り当ての交点になっている場所(黄色のセル)は初期コストとしてmin(0,10)=0を割り当てている。
邪魔なコンピュータの多段退避
邪魔なコンピュータを退避させるときに、退避先となる空白セルが存在しない場合がある。特に密な盤面において発生しやすい。
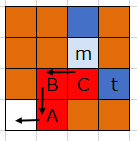
例えば以下の図において、Cを経由して t→m へコンピュータを移動させたいとする。このときCを退避させる必要があるのだが、Cは身動きをとれない状態である。このとき多段退避を行う。
まず、Cに隣接する4点それぞれで、さらにBFSによる退避を試す。仮にBを退避させるとする。
同様にBも身動きがとれないので、Bに隣接した4点それぞれで退避を試す。Aを退避させるとする。
Aの退避には成功するので、その後Bを元々のAの位置に移動、Cを元々のBの位置に移動することで、Cの退避に成功する[4]。
この多段退避の実装は再帰的なものになる。
参加記
後から書いたので考察の順番はかなり前後しています。記憶の改ざんがあるかも。
1日目
問題文を読んで軽くビジュアライザを眺める。難しい!焼きなましもビームサーチもできる気がせず、全然方針が思い浮かばない。
何はなくともビジュアライザを動かさなければならないので、自明解を出力できるように考える。最も単純には移動なしで、接続できるものを貪欲に接続するのが楽だろう。実装して出してみると 18,049 点。
ビジュアライザを見ると、縦にしか接続しないバグがあったので直す。いくらなんでも移動をしないのは自明解としても単純すぎるので、各コンピュータを最大1マス動かす処理を入れて提出。39,601 点。
この時点でのビジュアライザ結果が以下 (パラメータの幅が広い場合、考察用ケースとしては中点値~ちょい難を使うことが多く、K=4,N=33 を生成して使っていた。)

スコアはクラスタのサイズの二乗に比例するので、大きいクラスタを1個だけ作ったほうがいいように思う。この解は744点なのだが、仮に100個全て使うクラスタがあれば4950点を得られる。
試しに手編集で現状の解をいじってクラスタを拡大してみると、下画像のような状態になった[5]。

中点値のケースでは十分に疎であり、無理なくクラスタを拡大して1000点を超えるようなものが作れることが分かった。
手編集で行った操作を再現する方針で考えると、既存の最大のクラスタから線を張れる場所に、同色のコンピュータを持ってくる貪欲になる。それは多始点BFSでできる。
もちろん、同色のコンピュータが他の色のコンピュータに囲まれて動けない場所にある場合、先に邪魔なコンピュータを退避させなければならないんだけど、最初はそこは無視していいでしょう、ということでBFS貪欲解を実装。初期クラスタは、コンピュータを動かさずに作ったクラスタのうち一番大きいものにする(後に、単純に1点を選ぶ方式に変更)。
提出すると 199,460点。めちゃめちゃ上がって暫定1位になった。筋はよさそう。
暫定1位の記念ツイートをした。私は普段スタートダッシュだけ強いので、暫定1位になることはよくある。普段は後半でどんどん順位が下がって2桁後半の順位になるので、今回もそのパターンだろうと思っていた。
2日目
BFS貪欲解を改善するには当然、邪魔なコンピュータをどかす動きを実装するのが最優先である。どうやって実装するか分からないが、とりあえず簡単なケースだけアドホックに対処できるようにして 205k。
他色のコンピュータ上の通過を許可して経路作成→経路上の邪魔なコンピュータを退避させる、という形にするとよさそうだと思いつく。ただし退避が必要な経路はなるべく選びたくない、という気持ちになり、それができるのは他色のコンピュータ上の通過にペナルティを与えるダイクストラである。ということで解法にあるダイクストラを実装。この時点では「移動コスト:他色コンピュータのコスト」を「1:1000」と極端にしていた。さらに貪欲を時間いっぱい回すようにして 257k。
BFS貪欲解の時点で、疎な盤面では1色目をほとんど完全に接続できていた。ということは2色目をどれだけ大きくできるかを競うことになるだろうと想像する。AHC010で「2つの系列を同時に育てる」戦略をとっていた人がいたような覚えがあり、今回はこれが有効そう。初期値を2色選んで交互に拡張させる、陣取りバトルのパターンを追加。ビジュアライザを眺めるとBlokusを2人プレイしているように見える。1色の場合と半々で選ぶようにする。さらにダイクストラのパラメータを調整して 283k。
退避の動きをDFS->BFSに変更したり、初期値が2色の場合2色が同じ大きさのクラスタにしかならないバグの修正などをして 299k。 300k一番乗りになりたいという欲が湧いたのでダイクストラのパラメータを調整して提出すると... 0点。間違ってデバッグモードで出してしまった。30分後無事に302kを出すことができ、記念ツイート。
3日目
1色目を中央付近に配置→2色目を外枠付近に配置できればよさそうだと思って簡単に実験していたが、スコアには寄与しなさそう。そのうち直すかも (結局採用してない)。
とりあえずちょっとしたバグを修正して304k。

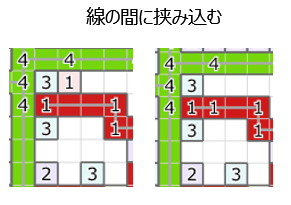
貪欲の途中にこのような盤面が現れることがあるが、右にある2を2-2の線の間に挟みこみたいと、しばらく前から思っていた。ダイクストラを修正してこれに対応し 319k。
4日目
寝て起きるとアイデアが浮かぶ。線を引く予定の場所は利用不可能と思っていたが、実は「まだ線は引かれていない」ので、コンピュータが移動・退避するときに通過点として使うことは可能だった。それに対応して 327k。

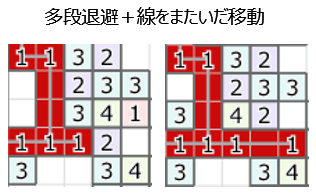
このような盤面から右にある3を下の3と繋ぐには、先に上の1を退避させてから中央の1を退避させる、という多段の退避処理が必要になる。それはずっと前から分かっていたが、どう実装できるのか考えついていなかった。
解法に書いたような再帰で対応できそうなことが分かったので実装。悩んだ割に実装量は数行で済む。この時点では深い多段に対処できるとは思っておらず、先にどかすのは1個までという限定をつけていた。これで347k。
350kを超えたいという欲がまた湧いたので、ダイクストラのパラメータを調整して提出。356k。Twitterがざわついているのを眺めて悦に浸る。
優勝は厳しいだろうけど、ここまでくるとさすがに1桁順位はとれるんじゃないかと思い始める。
ABCに出場。黄パフォで1918に到達。そろそろ黄色が見えてきたかも?
5日目
これまでダイクストラをして取り込み対象のコンピュータ候補を何点か列挙した後に、取り込みを試していた。貪欲前提だとここはダイクストラの内側で取り込みの試行を行い、成功すれば早期breakができるのでやや高速化できる。
この時点でパフォーマンスのボトルネックになっているのがどこかをgprofで見てみる。ダイクストラが重いようなので、少しだけ高速化。
多段の退避を1段より多くしてみて動くか確かめる。なんとそのままで動いてしまった。段数の上限を増やすごとに、密な盤面が目に見えて改善する。たぶんこれはそのままスライドパズルのソルバーみたいになっているんだと思う。最終的に5段を上限にした。
この時点で、密盤面専用のソルバーを作るプランは撤回。
さすがにこれは隠したほうがいいのではないかと思い、少し寝かせて提出し387k。再度Twitterがざわついているのを眺める。
AGCに出場。レートが惜しいのでUnratedで出場し、堂々の0完。危なかった。
6日目
ダイクストラをもう少し高速化した。
ここまで既存のクラスタ内のコンピュータを動かしていなかったのだが、クラスタ内のコンピュータ側を動かしたほうがいい場合もあるだろうとは思っていた。
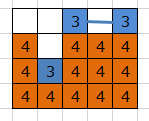
例えばこの盤面では、下の3を上に移動させて右向きに線を引くのは2+1手かかるのだが、上中央の3を左に移動させて下向きに線を引くのは1+1手で手数を節約できる。
これまでのコードの前提がいくつか崩れるので実装イヤイヤ期に陥っていたが、何とか実装。しかしスコアは変わらない~少し悪くなっているように見える。もしかしたら改善しているのかもしれないが、これをやった方がいい場面というのは少ないかもと思い、とりあえず破棄。
久しぶりに1位から落ちる。まあそう簡単にはいかない。他にも超強い人が潜伏しているかもとびくびくする。
7日目
もうとくにやることがないので、適当に高速化。2次元配列を1次元に直していく。
あとはハイパーパラメータの調整をAWS上で実施。どうやら疎盤面では、クラスタの初期値を2点選ぶほうの優先度を高めたほうがいいらしい。
12時に最終提出し、391kで暫定1位。あとは運を天に祈るのみ。
2人に追い越されて暫定3位でフィニッシュ。400kは完全に無理なので、素直に負けです。
システスで1個順位を落として4位。MMガチプレイヤーは強い。
感想
乱択貪欲をぶん回すのが好きな人間としてはとても楽しめました。上位陣は焼いている人が多いようですが、疎な盤面で焼けるとはまるで考えもしませんでした。私の実力で焼いていたらまずこの順位にはなっていないので、解法ガチャで☆5を引いたと思っています。
かつてないほど良い順位が取れました。昨年の日本橋ハーフマラソン増刊号も、これまでのRatedヒューリスティックコンの最高順位だったので、おそらく問題の相性がいいんだと思います。初の赤パフォでレート2354。橙を狙える位置に来ました。
追記
後日、貪欲の操作結果をビジュアライザで1手1手動かすと、実装した挙動がうまく動いているのが見えて楽しかったので、いくつか貼り付けます。


Discussion