トヨタ自動車プログラミングコンテスト2024#6(AtCoder Heuristic Contest 034)解法
問題ページ
解法概要
愚直な貪欲をベースに、なんとか焼けるものを探して焼いた。
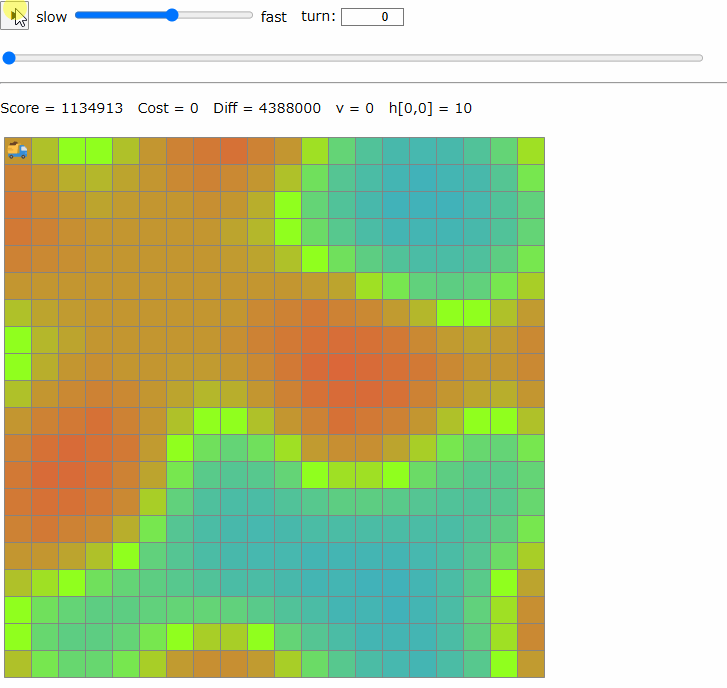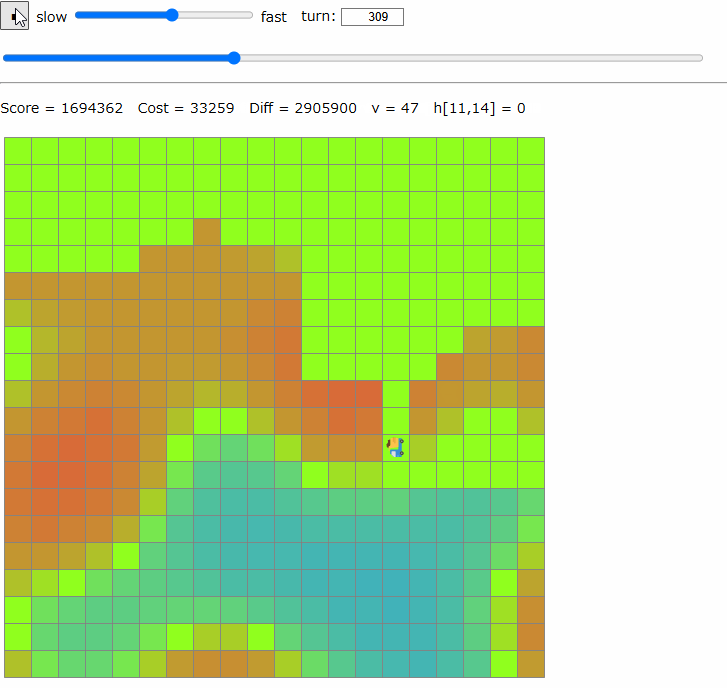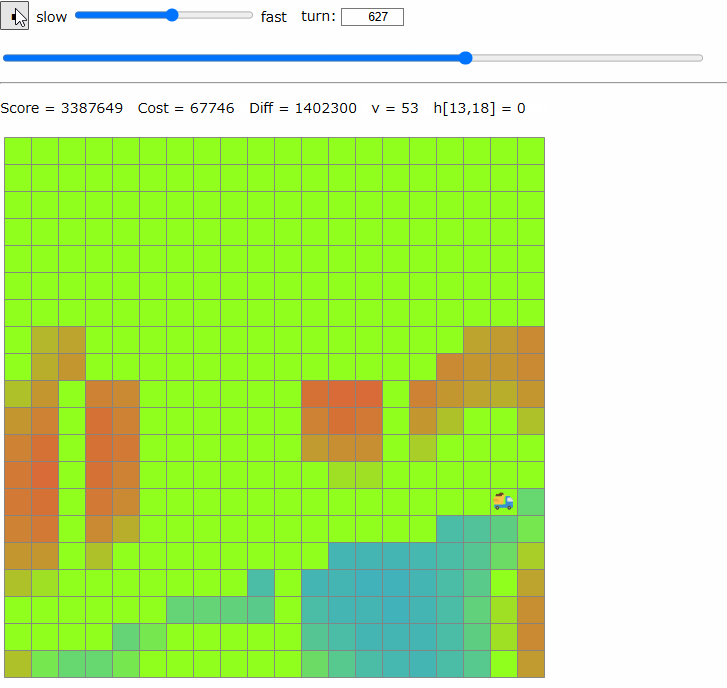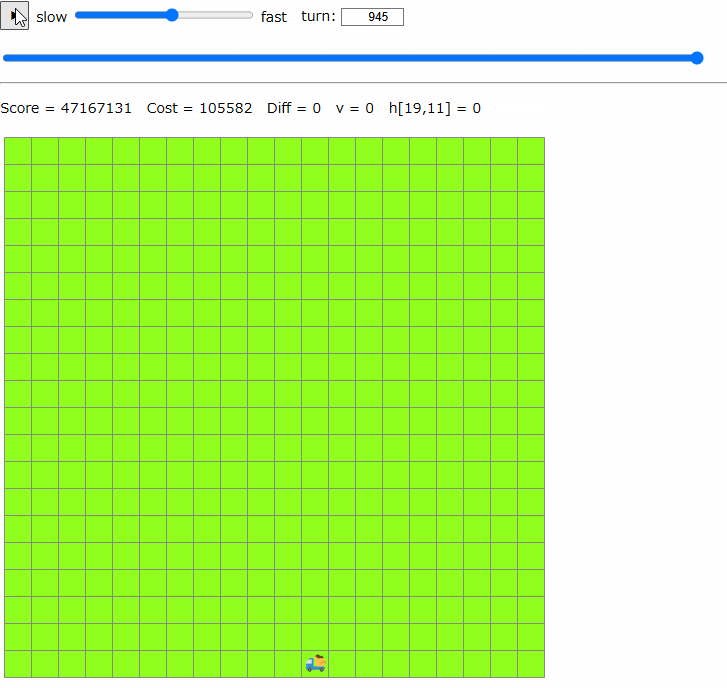
貪欲解法
30分時点で以下のような「積み降ろしにより平らにできる最も近いマスに行く」ことを繰り返す貪欲で暫定1位になり、この貪欲をベースにすることを決めた。自然な発想の解法だと思う。
以降、「山」は初期状態で高さがプラスのマスを、「谷」は初期状態で高さがマイナスのマスを指す。
- 山または谷のマスのうちダンプカーから最も近いマスに移動する
- 山に到達したらそのマスが0になるまで土砂を積む
- 谷に到達したらそのマスが0になるまで土砂を降ろすか、0にできない場合はダンプカーの積載を全て降ろす
- ダンプカーの積載量が200以上のときは山への移動はしない
- ダンプカーの積載量が0のときは谷への移動はしない
積み回数の列の焼きなまし
貪欲を書いた後、まあこれは経路を焼きなます系の問題なんだろうなあと思い焼く方法を考えていた。
ただ、積降ろしを一か所でも変えてしまうとその後に積める場所、降ろせる場所が全く変わり、解が別物になることが推測された。整合性を持ったまま焼くのは自分の実装力では厳しく、できたとしても計算量的にまともに動かない予感がした。
何か焼けるものがないかと思いつつ、貪欲解のビジュアライザを眺めながら改善の方法を考えたところ、下のような動きを改善したい気になった。

これは山を2マス回収したところで積載量上限の200に到達したため、1マスだけ山を残して谷に向かい始めたケースである。明らかに残りの山も回収したうえで谷に向かうほうがよい。
問題は積載量上限を200と固定していることで、今回だけ上限を増やせば山が1マス残ることはないはずである。この件に限らず、積載量上限が固定というのは柔軟性に欠ける気がする。
ここで貪欲の動きを再度考えると、おおよそ 「山の多いエリアに行って積載量200を超えるまで何マス分か積む→谷の多いエリアに行って降ろせるだけ降ろす→山の多いエリアに行って積載量200を超えるまで何マス分か積む→谷の多いエリアに行って降ろせるだけ降ろす→...」という感じの動きになっている。
これを可変になるように一般化すると「山の多いエリアに行って山 X1 マス分だけ積む→谷の多いエリアに行って降ろせるだけ降ろす→山の多いエリアに行って山 X2 マス分だけ積む→谷の多いエリアに行って降ろせるだけ降ろす→...」という動きになる。
積み操作を連続して行う回数の列である (X1, X2, ...) が可変になるが、これくらいなら問題なく焼くことが可能であろうと判断して焼くことに決める。
上記の画像の例だと、最後の方が「山2マス分積む、谷に行って降ろす、山1マス分積む、谷に行って降ろす」という動きだったのが「山3マス分積む、谷に行って降ろす」という動きになることが期待される。
焼きなましの制約としては X1+X2+...+Xm = (山マスの個数) となるような自然数列であればなんでもよい。
遷移としては以下の3種類を用いる。
- 2点選んで +1 と -1 する
- Xi と Xi+1 を合体させる
- Xi を分裂させる
評価関数としては、(X1,X2,...) の数列に沿って実際に貪欲を動かしてコストを求める。
直感的にはちょっと数列を変えたらダンプカーの動きが全く違ったものになると想像されるのだが、意外とまともに動いた。実際ダンプカーの動きがどの程度変わるのかは分かっていない。
小さい区間の微調整
操作系列として (積みまたは降ろし, マス, 土砂の量) の列を考える。移動は自明なので省略できる。
例えば以下のような valid な操作列があるとする。
[(積み, (1,2), 5), (積み, (1,3), 10), (降ろし, (3,3), 7), (降ろし, (4,4), 6), (降ろし, (3,4), 2), (積み, (3,5), 20) ]
このとき、積みが連続している区間か、降ろしが連続している区間は、順番を入れ替えても解として成立する。操作列を積みが連続しているまたは降ろしが連続している小区間に分割して、簡略化のため操作の番号だけ残してみる。
[[1,2], [3,4,5], [6]]
この小区間の内部で操作の順番を入れ替えた [[2,1],[4,5,3],[6]] のようなものは、不正な解にはならない。さらに、小区間に入るときと出るときでダンプカー上・マス上の土砂の量は不変であるため、小区間の外への影響がない。
先述の貪欲焼きなましで作った解に対して、後処理としてこの小区間の順番入れ替えによる微調整を行う。実際には小区間内で2点swapをする焼きなましを行った。
この焼きなましにより、貪欲解で生じた細かい無駄の改善ができる。
個々の小区間の長さが短いなら全探索やbitDPで最適解を求めることも可能だと思われる。
実際に実装を試したところ、コンテスト中の約1時間が虚無に溶けていった。私の実装力で手を出してはいけない方針だった。
貪欲の評価関数について
コンテスト後に気づいたことだが、これは基本的に貪欲解法なので評価関数が重要である(当たり前すぎる)。
上記解法ではダンプカーから最も近いマスに移動するという評価関数を使っており、それはそれでいいのだが、距離が等しい山や谷が複数ある場合にどのマスを優先するかというタイブレークを考えていなかった。

3種類のタイブレークについて、それぞれ貪欲の途中状態を示している。左から
- 距離が等しい山・谷が複数ある場合、ランダムに1マス選ぶ
- 距離が等しい山・谷が複数ある場合、上側にあるマスを優先して選ぶ
- 距離が等しい山・谷が複数ある場合、外周にあるマスを優先して選ぶ
となっている。タイブレークが違うだけなのに全く違う盤面になっていることが分かる。
コンテスト中の提出はタイブレークについて何も考えていないものであり、上側優先に自然となっていた。しかしコンテスト後に実験してみたところ、外周優先の方が明らかに強かった。山や谷のある場所が中央に密集するようになり、平均的な移動距離が減るものと考えられる。
点数
コンテスト中の提出(積み回数の列の焼きなまし + 小区間内の順番の焼きなまし)
8326M点 で17位
コンテスト後の提出(上記+貪欲を外周優先)
8677M点で本番8位相当になってしまった。なんてことだ。
Discussion