【数学】今日の気づき
glassonion1線形代数、サラスの方法
3次正方行列の行列式を求める方法(サラスの方法)。オライリーの「実例で学ぶゲーム3D数学」のこの図が一番わかりやすかった。
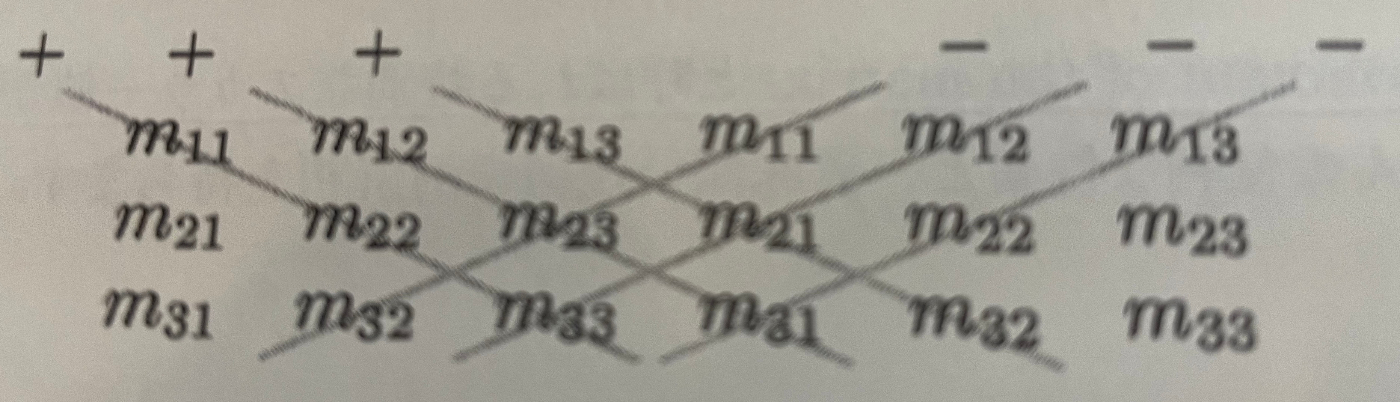
これまでいろんな本の解説や図をみたけど、いまいちわかりづらく覚える気にならなかった。サラスの方法使う場面あるのかって話だけど文字列を含む行列式の場合はわりと使い勝手が良い。
glassonion1統計学、分散と共分散
「入門はじめての多変量解析」P26の分散と共分散の説明。統計学の本でこのようなわかりやすい説明はなかったのでとてもありがたい。
分散は長さの概念であるのに対し、共分散は広がりの概念です。
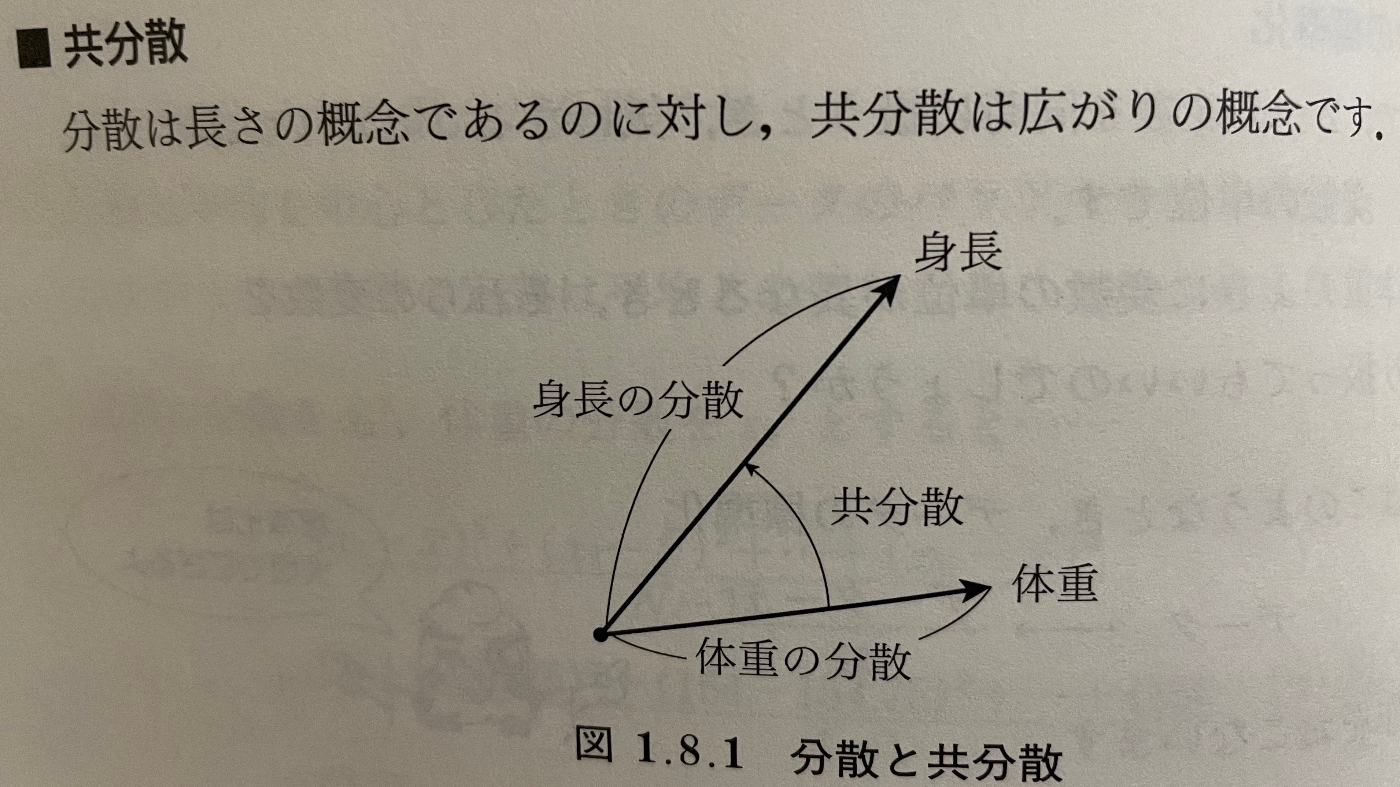
統計学の本、正直なところあまり良い本がないから、多変量解析から入るのがよい気がした。
glassonion1微分、関数の最小値
微分に対する重要な気づき、最小二乗法を勉強していた時に気づいた。2次関数の最小値問題が微分で解けることを知らなかったのでこれは重要な気づき。
glassonion12次関数の最小値問題平方完成よりも微分のほうが簡単だと思っていたけど、河野玄斗さん平方完成の動画観て考えが変わった。この動画のテクニックを使うと秒で平方完成できるので微分よりも早く問題が解ける。
glassonion1行列式の幾何学的意味
2次正方行列の行列式は平行四辺形の面積なのか。ここから三角形の面積も簡単に計算できる。
この解説をはじめて見たのは確かこの本。
もっちょさんのこの記事も必読
glassonion1統計学、標準偏差
分散のルートをとったものがなんで標準偏差とい名前なのか疑問だったけど、データを標準化するときの分母になるからだと気づく。機械学習とか多変量解析の勉強をはじめてからデータの標準化の大切さがわかってきた。統計学の本はもっと標準化についてちゃんと説明しろよと思った。
「入門はじめての多変量解析」P25
glassonion1
決定係数R^2
評価指標入門に書いてあった。モデルが線形か非線形かは常に意識したほうが良さそう。
glassonion1ベクトル空間？空間って何？
3D空間みたいなものを勝手に想像してたけど全然ちがった。「どうして多項式がベクトル空間になるんだよ」って同じことおもった。本を読んでもピンとこなかったがこの動画を観て理解することができた。
あとこのツイートもよかった