E資格対策 16-17章

 16章：深層学習を用いた生成モデル回答した問題
ア:B，イ:A，ウ:D，エ:D　※イ等を復習
ア:，イ:，ウ:D  ※全く分からず
ア:D，イ:C，ウ:D，エ:A，オ:A　※要整理，ほぼ全く分からず
A
ア:D，イ:C，ウ:C，エ:C ※何も分からない
回答した問題②
ア:B，イ:A，ウ:D，エ:D
ア:A，イ:C，ウ:C　※KLダイバージェンスについても添付する
ア:D，イ:B，ウ:B，エ:A，オ:C　※モード崩壊についても纏める，
B
ア:B，イ:A，ウ:C，エ:D
間違った問題

2. イ:C→A　※最適な生成器と識別器の出力について

GIBA

 生成モデルのモデリング（識別モデルとの違いを基に）
識別モデルのモデリング:

確率モデルに基づいてC_{\text{pred}}を得ることが目標である。そのため，入力xが与えられた際の事後確率を最大とする値\underset{C}{\arg\max} \, p(C \mid x)を解くことになる。そのため，モデリング対象はp(C|x)である。

生成モデルのモデリング:

確率モデルに基づいて新しいデータをシミュレートしたり，生成されたデータのクラスラベルC_{\text{pred}}を予測したりすることが目標である。そのため，P(x|C)とP(C)をそれぞれモデリングするか，同時確率P(x,C)をモデリングして，\underset{C}{\arg\max} \, p(x,C)を解く。
ベイズの定理が以下のように表されるため，上述した2つのいずれかを解けばargmax_{C} p(x,C)を解ける。最終的には同時確率p(x,C)をモデリングしたい。

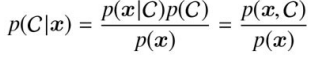
 データの生成確率・クラス予測データ生成確率を計算するためには，同時確率分布p(x,C)を用いる。具体的にはクラスラベルに対して周辺化(積分または和を取る)することによって得られる。

p(x) = \sum_{C} p(x \mid C) p(C)
クラス予測の場合，データが与えられたときそのデータが属するクラスをベイズの定理を使って求める。そして，最も高い条件付き確率を持つクラスを予測結果として選ぶ。

p(C \mid x) = \frac{p(x \mid C) p(C)}{p(x)}

 変分自己符号化器(VAE:Variational AutoEncoder)

https://cvml-expertguide.net/terms/dl/deep-generative-model/vae/

VAEはエンコーダとデコーダがそれぞれ確率分布として表される。エンコーダは入力データxを潜在変数zの分布にマッピングして，デコーダは低次元の潜在変数zにエンコードする際，分布を仮定する。この分布からサンプリングすることで新しいデータを生成することが可能となる。

モデリングの対象はp(z)と確率分布p(x|z)である。
潜在変数の事前分布p(z): 潜在変数zを使って観測データxを生成するため，まず潜在空間の分布をモデル化する必要がある。これにより後段の処理で潜在空間から新しいデータを生成することができる。通常，事前分布p(z)は標準正規分布\mathcal{N}(0, I)として仮定される(つまり固定された分布であり学習されない)。
尤度p(x|z): 潜在変数zが与えられた時にデータxがどのように生成されるかを学習できる。この条件付き分布をデコーダが学習することでVAEが新しいデータを生成することが可能となる。
事後分布p(z|x): データxが与えられたときの潜在変数zの分布は直接モデリングしない。代わりにエンコーダが近似分布としてq(z|x)を学習する。具体的には，エンコーダはガウス分布(正規分布，\mathcal{N}(\mu(x), \sigma^2(x)))を仮定し，観測データxに基づいて潜在変数の平均\mu(x) と分散\sigma^2(x)を出力する。

※事前分布p(z)と近似分布q(z|x)の間に距離(KLダイバージェンス)を測り，これを最小化するようにエンコーダを学習させる。これにより，新しいデータを生成する際に無理のない事前分布(正規分布)に従った潜在変数から合理的なデータを生成できるようになる。

 VAEの目的と定式化
目的: VAEは観測されたデータを元に似たような新しいデータを生成することである。つまり，あるデータxが観測されたとき，そのデータが生成される確率を最大化すること。推論時には，学習済のデコーダ部分を利用して潜在変数zから観測データxを生成する使い方をする(zは正規分布として仮定されているp(z)からサンプリングする)。つまり，何等かの潜在変数zがあり，それがデータxを生成すると考える。

方法: データがうまく生成できる確率(周辺尤度)を最大化する(尤度の最大化=観測されたデータがあるモデルによって生成された確率を最大化すること)。つまり，観測されたデータを再現できるモデルを学習する上で，観測データ(例: 猫の画像)が観測される確率(周辺尤度p(x))を最大化するアプローチが目的を達成する上で必要となる。しかし，この周辺尤度の計算に含まれる積分を解析的に解くことは難しいため，VAEは周辺尤度を直接最大化するのではなく，変分下界(ELBO)という近似的な方法で周辺尤度を最大化するアプローチをとる。
周辺尤度p(x)はデータxがどのように生成されたのかを総合的に評価する確率である。つまり，潜在変数がどんな値であってもデータxが生成される可能性を全体として評価するものである。そのため，潜在変数zの全ての可能性について，それぞれの潜在変数からデータが生成される確率を計算してそれを全て足し合わせていく↓。

p(x) = \int p(x \mid z) p(z) dz

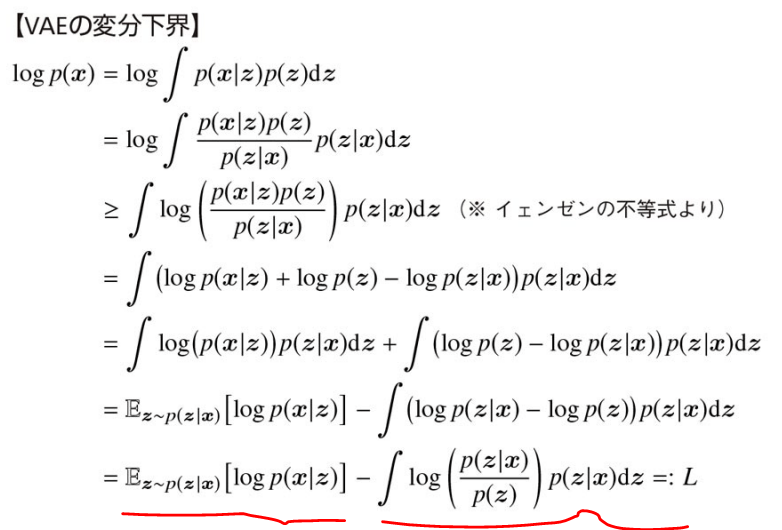
 学習方法上記で少し触れたようにVAEの目的は周辺尤度p(x)を最大化することである。学習時には，対数尤度\text{log}p(x)を最大化することを目的として\text{log}p(x)を以下のように変形する。以下変形により下界L(ある量が持つことができる最も低い値)を得るため，このLを最大化するように学習を行う。

第1項(ELBO項, 再構成誤差): デコーダで再構成された学習データに対する対数尤度の経験期待値として近似できる。本項は，エンコーダとデコーダが協力して入力されたデータxをどれだけ正確に復元できたかを測定する項。
第2項(KLダイバージェンス): p(z|x)が想定している確率分布p(z)(正規分布)とかけ離れないための正則化として機能する。これは，第1項だけを最小化するように学習すると潜在変数zが事前に過程した標準正規分布から遠く離れたものになってしまう可能性があるためこれを防ぐ。

https://ja.wikipedia.org/wiki/カルバック・ライブラー情報量

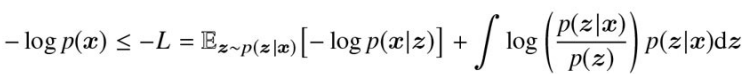
NNのような勾配法に基づくアルゴリズムは最小化問題を解くように実装されることが多いため，学習時には下界Lの符号を反転させることで最小化問題へと変換する。そしてデコーダのパラメータおよびエンコーダの変分パラメータを交互に同時学習していく。

ここで，デコーダの出力が分散一定の正規分布に従っていれば，-text{log}p(x|z)はデコーダの出力x'を使った二乗損失\frac{1}{2} (x - \hat{x})^2に置き換えることができる。

これは，正規分布(ガウス分布)の対数尤度の形が二乗損失と同じ形式であるため置き換えられる。以下ガウス分布の確率密度関数の対数を取った式。

\log p(x \mid z) = -\frac{(x - \hat{x})^2}{2\sigma^2} - \log \sqrt{2\pi \sigma^2}

 再パラメータ化トリック(Reparameterization Trick)

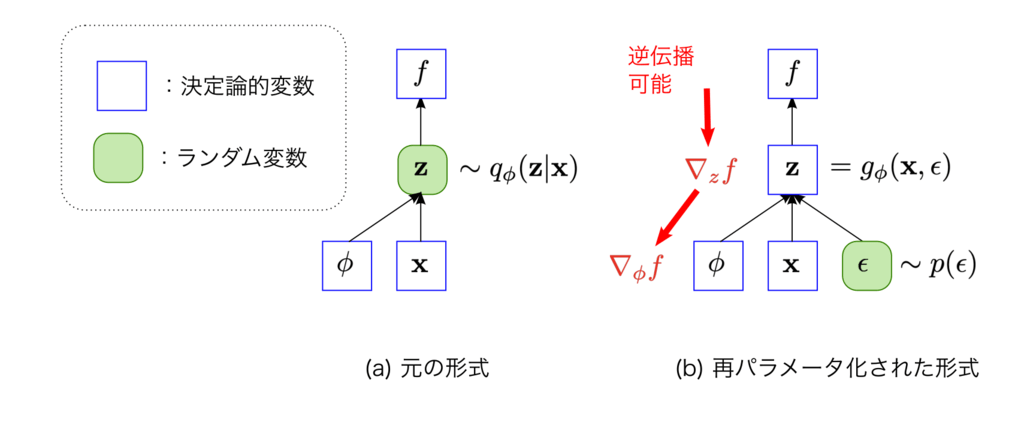
エンコーダの近似事後分布q(z|x)を用いてzの正規分布のパラメータ(平均と分散)を推定した際にそのパラメータからデコーダに渡す潜在変数zをサンプリングする必要がある。しかし，サンプリング処理は微分不可能であるため，VAE全体(エンコーダ部分)に損失をバックプロパゲーションすることができない。これを解決する手段が再パラメータ化トリック(Reparameterization Trick)である。
具体的には，以下でサンプリングされるエンコーダ出力である潜在変数z，つまり平均\mu(x)と分散\sigma^2(x)を

z \sim \mathcal{N}(\mu(x), \sigma^2(x))
これは平均が\mu(x) で分散が\sigma^2(x)のガウス分布から潜在変数zをサンプリングするという意味
外の別の確率変数\epsilon(標準正規分布からの値)に対してエンコーダの出力である平均\mu(x)と分散\sigma^2(x)を使って線形変換する。線形変換で表現されているため微分することが可能となる。(例:潜在変数zに対する平均\mu(x)の微分)

z = \mu(x) + \sigma(x) \cdot \epsilon

 補足: 最適な生成器と識別器が両方得られた場合の識別器出力結論: 0.5

理由:これは，識別器Dが生成されたデータと本物のデータを区別できなくなるためランダムに確率を出力するようになるため。

https://dreamer-uma.com/gan-theory/

 補足: 各種トリック
 対数微分トリック(log derivative trick):掛け算を足し算に変換できるという対数の性質を利用して微分を簡単化する方法。例えば，掛け算を含む複雑な関数を微分するとき，対数を取ることで式が簡単になり，計算がしやすくなる。これは確率分布や期待値を微分するときにも役立つ。以下具体例

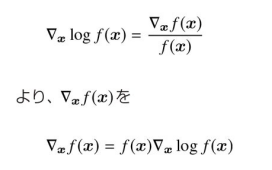
対数を取る:

\log f(x) = a \log x
これを微分する:

\frac{d}{dx} \log f(x) = \frac{a}{x}
対数を戻すと、元の関数の微分が得られる。

 カーネルトリック(kernel trick):SVMを中心に用いられる高次元空間に写像されたデータ同士の内積を高速に得る手法のこと。

 ハッシュトリック(hashing trick):単語などの入力データをハッシュ関数によって変換する手法のこと。

 敵対的生成ネットワーク(GAN:Generative Adversarial Network)https://cvml-expertguide.net/terms/dl/deep-generative-model/gan/
GAN (敵対的生成ネットワーク) とは，敵対的学習(Adversarial Training)を用いて深層生成モデルの学習を行う，生成器Gと識別器Dのネットワークペアである．敵対的学習を行うことにより，「学習データ分布とそっくりな，本物らしいデータ]を生成することができる生成器Gを，データ群のみから教師なし学習できるのが，GANの一番の特徴および利点である．
敵対的学習: 2つのNNジェネレータGとディスクリミネータDのペアをお互いがもう片方の評価をして競い合い交互学習させる仕組みにより，ジェネレータの学習方法。

 学習方法ないし目的関数

敵対的学習は，以下価値関数V(D,G)を目的関数として用いてGとDの交互最適化を行う。十分に学習が進むとナッシュ均衡(分類器が生成した画像に対して全て1を出力する)に達し，これが解になる。

※text{log}D(x)は1を，text{log}D(\hat{x})は0を出力するようにしたい

※text{log}D(\hat{x})が1を出力したい
補足として，GANの最適化問題は，JS-divergenceの最小化問題とみなせる。

 DCGAN(Deep Convolutional GAN)の学習安定化方法GANのCNN化とそれに伴う以下学習安定化方法が以下のように提案されている。
プーリング処理の代わりに、ストライドを2以上に設定した畳み込み層や逆畳み込み層を使用

理由: プーリング層では情報の一部が失われる可能性があるが、ストライドを大きくすることで同様の効果を得つつ、より多くの情報を保持。逆畳み込み層は生成器において解像度を高めるのに有効(以前はアップサンプリングやプーリングの逆操作を適用していた)。
生成器と識別器の両方にバッチ正規化を使用

理由: バッチ正規化によって各層の出力が適切にスケーリングされ、勾配消失や爆発を防止。これにより、学習の安定性が向上し、モデルの収束も促進される。
生成器の活性化関数は、最終層にtanh、それ以外の層にReLU (Nair & Hinton, 2010) を使用

理由: ReLUは勾配消失問題を緩和し、活性化がゼロになる問題が少ないため、深い層での学習に適している。最終層のtanhは、生成画像の出力を[-1, 1]に収めるために使用(以前は最終層にsigmoid等を利用していたため，[0, 1]の範囲でしか表現できなかったため表現力が乏しかった)。
識別器の活性化関数にLeaky ReLU (Maas et al., 2013) を使用

理由: Leaky ReLUは負の値にも小さな勾配を持たせるため、識別器の学習を安定化させ、勾配消失を防ぐ効果がある。
全結合層は使用しない

理由: 全結合層はパラメータが多く、過学習や非効率な学習を引き起こしやすい。畳み込み層を活用することで、より効率的に空間情報を保持しながら学習を行う。

 条件付き敵対的生成ネットワーク(CGAN:Conditional GAN)

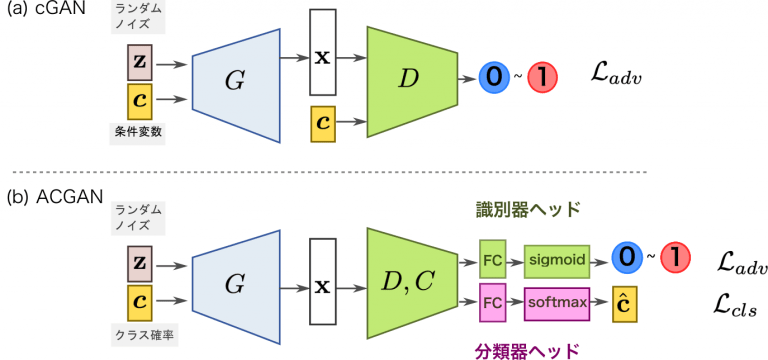
CGANでは条件変数cの値に条件付されて変化するG(z|c)として生成器を学習する仕組みが提案された。cはクラスラベルのスカラー値でもよければテキストや画像データ等の補助クエリベクトルも使用できる。

ACGANは識別器D側がクラス識別も行うマルチタスク学習を行う。

 pix2pix

https://toukei-lab.com/pix2pix

CGANの条件を画像とすることでスタイル変換を行うのがpix2pix。例えば，エッジ(線画のスケッチ)からカラー写真への変換タスクを学習する場合，エッジ画像を条件として生成器，識別器それぞれに与える。
生成器: 乱数zと条件画像からスタイル変換を施した画像を出力。
識別器: 「条件画像と変換された画像」と「条件画像と本物画像」から偽物の組み合わせと本物の組み合わせを判断し，各ペアからそのペアが本物である確率を出力。

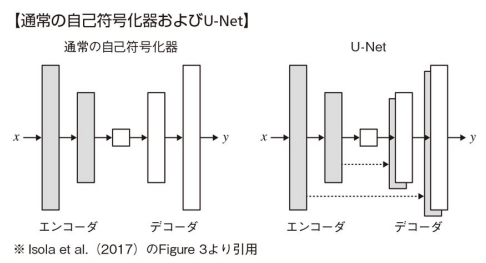
生成器にはU-Netというセマンティックセグメンテーションアーキテクチャが用いられる。特徴は，上図灰色の矢印で示すskip接続し，エンコーダの情報をデコーダに渡して連結する。これで，画像の細かい特徴と抽象的な特徴の両方を捉えることができる。

具体例: 白黒画像からカラー画像に変換するタスクでは，入力画像のエッジ位置の情報をデコーダ側へ接続して共有することができる。

分類器にはPatchGANというというNNアーキテクチャを用いる。これはPatchという名の通り，画像の一部をパッチ単位で取り出してそのパッチ単位で真偽判定するアーキテクチャ。具体的には，パッチ毎に各パッチが本物である確率を出力し，この時パッチ毎の損失が個別に計算され，その平均が全体の損失となる(以下記述のGAN損失の部分)。
学習では，以下目的関数(損失関数)を解くように学習する。

以上損失は2つの項から成る。
GAN損失: 上述した一般的なGANの損失

V(G,D)= \mathbb{E}_{x,y}[\log D(x, y)] + \mathbb{E}_{x,z}[\log (1 - D(x, G(x, z)))]
L1損失: GAN損失のみだとターゲット画像にどれだけ近いかを保証できないためL1損失を追加。この損失は，生成された画像とターゲット画像との画素毎の差の絶対値の平均を計算してこれを最小化する。

これにより画像の大域的な情報を捉えられるようになり，違和感のない画像が生成できる。

L(G)=\mathcal{L}_{L1}(G) = \mathbb{E}_{x, y}[\| y - G(x) \|_1]
pix2pixの各種特徴纏め:
変換前画像(条件画像)と変換後画像のペアを用意する必要がある。
L1損失やL2損失は画像の低周波数構造(実空間における画像の全体的な構造)を良く捉えられるが，画像の高周波数の構造(実空間における細かい構造)を良く捉えられず画像がぼやける欠点がある。pix2pixでは，この欠点を解消するためPatchGANを用いて局所的な画像パッチの構造のみに注目する。パッチ径よりも離れた場所にあるピクセル間は独立であることを仮定し，識別器は画像の中でN×Nのパッチがそれぞれ本物か偽物かを判定する。

※なお，L1損失の方がL2損失より画像をぼかす効果が低い
高解像度画像への変換はしない。あくまでスタイル変換だけ。

GIBA

 第17章：深層学習を用いた強化学習回答した問題
ア:A，イ:D，ウ:B，エ:B
ア:B，イ:D，ウ:D，エ:A，オ:C
ア:C，イ:A，ウ:D
間違った問題
イ:D→B，ウ:B→D
イ:D→A，ウ:D→C
ア:C→D，ウ:D→C

GIBA

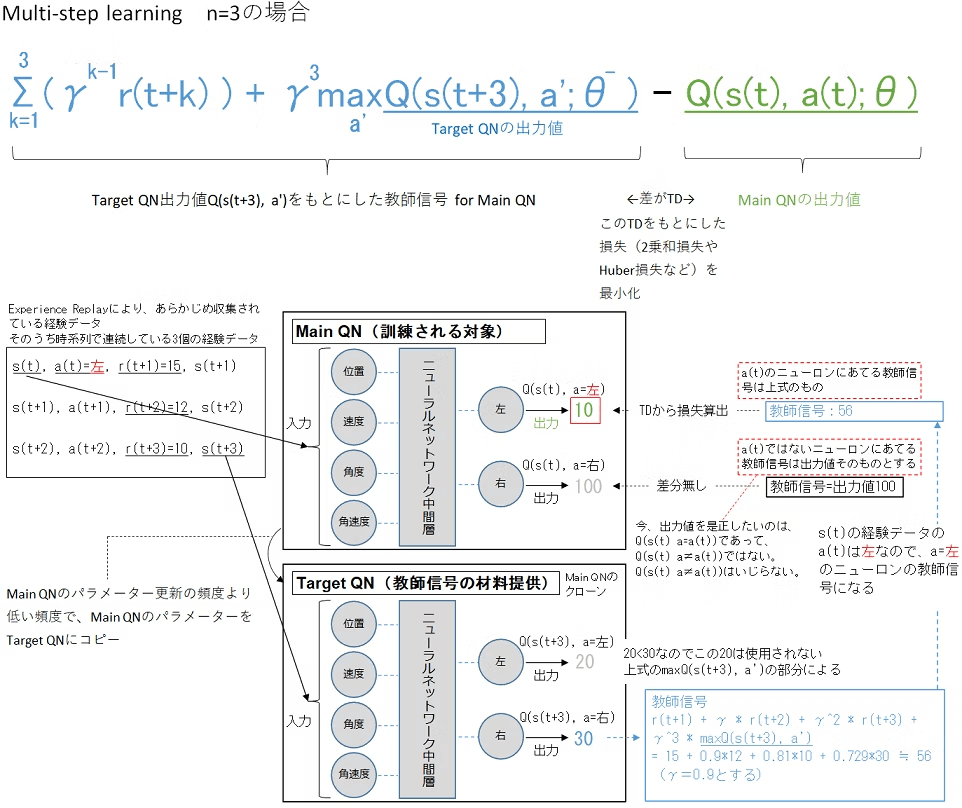
 深層Qネットワーク(DQN:Deep Q-Networks)https://qiita.com/wing_man/items/a9cb43711dbb188f1604

強化学習に深層学習を適用して成功したアルゴリズム。DQNはAtari2600の様々なゲームに対してチューニングをせずに学習しても高い性能を示した。

DQNでは，畳み込みニューラルネットワーク(CNN)によって行動価値関数を推定する。このCNNではある時点におけるゲーム画面のキャプチャ画像を状態として受け取り，その時点である行動をとった場合の推定価値を取り得る行動毎に出力する。

学習はQ学習の考え方に基づき行われる。つまり，CNNから出力される行動価値が目標とする行動価値に近づくように学習していく。

価値関数をDNNにより近似する手法は古くから提案されていたが，学習の安定性に課題があった。DQNでは，この課題を解決するために以下のような工夫が導入された。
経験再生(experience replay)
目標Qネットワークの固定(Fixed Target Q-Network)
報酬のクリッピング(Reward Clipping)

 経験再生(experience replay)通常の強化学習のようにエピソードの全軌跡(一連の状態sと行動a)と即時報酬の履歴を用いてNNを更新すると，訓練が安定しないことが知られている。なぜなら，これら入力データ(一連の状態s)は典型的な示威系列データであり，互いに独立ではないためにその影響を受けるから。

以下は経験再生のメリット。
同じ経験を何度も学習に使えるため，データ効率が良くなる。
ランダムに取り出された経験を用いて損失を計算するため，入力系列の相関を断ち切ることができ，更新の分散を軽減できる。
過去の様々な状態において，行動分布が平均化されるため，直前に取得したデータが次の行動の決定に及ぼす影響を軽減できる。

 目標Qネットワークの固定(Fixed Target Q-Network)目標Qネットワーク(Target Q-Network)とは学習対象となるメインQネットワークとは別に教師信号の元となるQ値(次の状態における最大のQ値と報酬を使って計算される値)を出力するだけが役割のNNを指す。このネットワークは学習の安定性を保つために使われる。
教師信号の元となるQ値: y = r + \gamma \max_{a'} Q_{\text{target}}(s', a')
メインネットワークとターゲットネットワークの違い:

項目
メインネットワーク (Online Network)
ターゲットネットワーク (Target Network)

役割
各状態に対するQ値を計算し、行動を決定する
ターゲットQ値を計算し、Q学習の更新式で利用する

更新頻度
毎ステップで更新される
数千ステップor1エピソードごとにメインネットワークの重みをコピーして更新

目的
エージェントの行動選択やQ値予測
Q値のターゲット値を計算し、学習の安定性を保つ

重みの更新方法
勾配降下法で損失関数を最小化する
定期的にメインネットワークの重みをコピーして更新

Fixedは，パラメータがメインネットワークよりも低い頻度である事を指している。Fixedなパラメータ(ターゲットネットワークのパラメータ)を\theta^{-}とした場合の損失関数は以下となる。

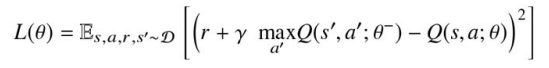
 報酬のクリッピング(Reward Clipping)エージェントが受け取る報酬の範囲を制限する手法。

 報酬クリッピングの方法報酬クリッピングでは、報酬を特定の範囲に収めるために、次のような方法が使われます：
定数クリッピング:
例えば、報酬を ([-1, 1]) の範囲内にクリップします。正の報酬はすべて (1) に、負の報酬はすべて (-1) に変換します。ゼロの報酬はそのまま (0) として扱います。
r_{\text{clipped}} = \text{clip}(r, -1, 1)ここで、( r ) は元の報酬、( r_{\text{clipped}} ) はクリッピングされた報酬です。
非対称クリッピング:
報酬の上限だけをクリップする、または下限だけをクリップする方法もあります。例えば、報酬が非常に高い場合にのみ上限を設けてクリップし、逆に非常に低い場合に下限を設ける場合です。

 報酬クリッピングの利点学習の安定性:
報酬の範囲を狭くすることで、Q値や価値関数の更新が一定の範囲に収まり、過剰に大きな更新が行われなくなります。これにより、学習が安定します。
学習速度の向上:
極端な報酬の影響を減らすことで、エージェントは報酬のスケールに関係なく学習を進めることができ、より一貫した学習を行うことができます。
一般化の促進:
クリッピングにより、報酬が単純化されるため、エージェントはより一般的な方策（ポリシー）を学習しやすくなることがあります。

 AlphaGohttps://qiita.com/RyuKahou/items/1812102ed05b2fdf7ffc

https://qiita.com/gifucom17/items/3096ac60522f8b815a32

 アルゴリズム構成SL(教師あり学習)方策ネットワーク
RL(強化学習)方策ネットワーク
価値ネットワーク
モンテカルロ木探索(MCTS: Monte Carlo Tree Search)
※ネットワークはCNNであり，碁石の画素として入力を受け取る

 学習過程以下3つのステージ構成で学習が進む。

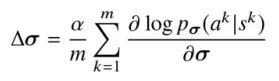
 「第1ステージ: 教師あり学習によって囲碁の熟練者の手をニューラルネットワーク(SL方策ネットワーク)に学習」盤面sのもとで人が選んだ手aに関する対数尤度の最大化を行うことでSL方策ネットワークを学習させる。学習時のパラメータ更新は，

を現在のパラメータに加えることによって行う。(

以上数式は，以下プロセスを示す。
各状態 s^k において、方策ネットワークが行動 a^k を取る確率 p_{\sigma}(a^k | s^k) を計算し、その対数を取る。
その対数確率を最大化する方向にパラメータ \sigma を更新する。これにより、ネットワークが次に状態 s^k に直面したときに、行動 a^k を選ぶ可能性が高まる。
これをバッチ内のすべての状態-行動ペアに対して平均を取り、最終的な更新量 \Delta \sigmaを得る。

ここでは，対数尤度を最大化するため勾配上昇法となることに注意。

 「第2ステージ: 第1ステージで最適化されたパラメータを初期値にして新たなニューラルネットワーク(RL方策ネットワーク)を学習する」学習されたSL方策ネットワークのパラメータを初期値としてRL方策ネットワークを学習する(そのため，構造は同一)。

RL方策ネットワークの学習は，現在の方策とこれまでの方策からランダムに選択された方策同士を戦わせる。ランダムに選択する理由は，現在の方策に対して過剰適合しないようにするため。

強化学習手法として，方策勾配法:RINFORCEアルゴリズム(直接方策を学習する)を用いる。学習時のパラメータ更新は，

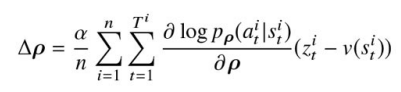
をパラメータに加えることによって行う。

本式はREINFORCEアルゴリズムに基づいて導かれており，各項の意味は以下。

\frac{1}{n} \sum_{i=1}^{n} \sum_{t=1}^{T^i}:
複数のエピソード n に対して，各エピソード内の全てのタイムステップ T^i についての平均を取っている。エピソードは個々の試行を表し，各エピソード内で時刻 t に対する行動の更新を行う。

\frac{\partial \log \rho(a_t^i | s_t^i)}{\partial \rho}:
方策 \rho(a_t^i | s_t^i) の対数確率の勾配です。これは、状態 s_t^i において行動 a_t^i を取る確率に対するパラメータ \rho の勾配を計算しています。

(z_t^i - v(s_t^i)):
優位度（Advantage）を表している。これは、状態 s_t^i における行動 a_t^i が、期待される報酬 v(s_t^i) と比較してどれだけ有利であったかを示します。

z_t^i は、ある種の累積報酬（例えば、割引報酬）を表しており、具体的にはその行動によって得られた報酬の合計値を示しています。

v(s_t^i) は、状態 s_t^i における価値（Value）を表しており、これはクリティック（Critic）ネットワークによって推定されます。
優先度が正であれば，その行動は期待される価値(前エピソードの学習により得られた状態の価値)よりも良かったことを意味し，方策はその行動を強化するように更新される。

 「第3ステージ: 価値ネットワークを学習させる 」※RL方策ネットワーク(Actor)に直接フィードバックを与えるものではない盤面sに関する価値関数を評価する。出力は-1から1の間の実数であり，(出力＋1)/2とすると，その値はそのゲームに勝つ確率と解釈できる。
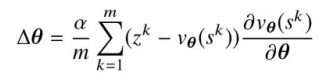
価値ネットワークの学習は，盤面sと正解ラベルを回帰させる。そのため，損失関数には二乗誤差を用いる。つまり，価値ネットワークが予測した価値と正解ラベル(上記更新式で示したエージェントが得た累積報酬)に基づいて誤差を計算する。学習時のパラメータ更新は，

を現在のパラメータに加えることによって行う。。本式の各項の意味は以下。

\frac{1}{m} \sum_{k=1}^{m}:
バッチサイズ m に対して各サンプル k について平均を取る操作を示しています。複数のサンプルに基づいてパラメータを更新するため、学習が安定しやすくなります。

(z^k - v_{\theta}(s^k)):
これは**TD誤差（Temporal Difference Error）**を表しています。具体的には、予測された価値 v_{\theta}(s^k) と、実際に観測されたリターン z^k との差を表します。この差が大きいほど、予測が不正確であることを示し、その誤差を最小化するようにパラメータを更新します。

\frac{\partial v_{\theta}(s^k)}{\partial \theta}:
価値関数 v_{\theta}(s^k) のパラメータ \theta に対する勾配です。これは、パラメータをどの方向にどれだけ修正すべきかを示します。

ここでは勾配上昇法ではなく，勾配降下法によって更新している。

また，価値ネットワークの学習は教師あり学習で行うため，事前にデータ集合を用意する必要がある。データ集合を作るための対戦では以下のような手順を踏む。

t=1,...,U-1の時間ステップにおいてSL方策ネットワークを用いて指し手を決定

t=Uの時間ステップにおいてはあらゆる手からランダムに(合法手になるまでのサンプリング)指し手を選ぶ。

t=U+1,...,Tの時間ステップにおいてはRL方策ネットワークを用いて指し手を選ぶ。

 推論(実践)過程学習した後，推論(実践)を行い囲碁をプレイする。実践では，相手の手を読む必要が生じる。

相手の手を読む行為はモンテカルロ木探索という方法を用いて行う(AlphaGoで用いられるモンテカルロ木探索のアルゴリズムはAPV-MCTSと呼ばれる)。

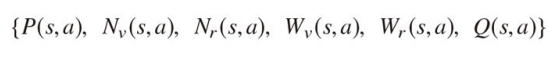
探索器の各々のノードsにはすべての合法手a(盤面のルール上許される全ての可能な手)に対するエッジ(s,a)がある。各々のエッジは以下統計量を保持する。

P(s,a): SL方策ネットワークによって算出される事前確率

Q(s.a): 行動価値

N_v(s,a): 木の末端で価値ネットワークを用いて評価を行った回数

W_v(s,a): N_v(s,a)回の評価に対する行動価値の総和。つまり，実際のシミュレーションをせずにネットワークが予測した結果(各状態s,行動aにおける価値)を全て合計する。

N_r(s,a): ロールアウトの訪問回数(同じ状態において同じ行動を行った回数がs,a毎に保存されている) ※ロールアウト: 囲碁の対戦simulationをして，ゲームを最後まで進めること。

W_r(s,a): N_r(s,a)回の訪問に対する行動価値の総和。つまり，実際にシミュレーションを行って，その結果どれだけ良い価値が得られたかの総和を表す。

APV-MCTSの概略は以下(以上図を参照)
選択(selection):

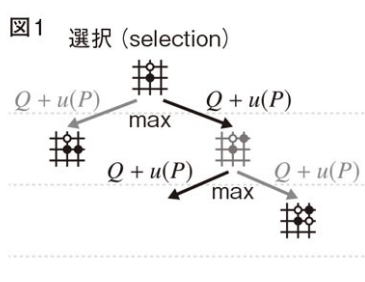
探索木のルート(現在のゲームの状況，つまり囲碁の現在の盤面)からシミュレーションを始め，葉(木の末端)に到達した時点で終える。つまり，自分がこの手を打ったら相手はどこに打つかということを木構造の中で次の手をシミュレーションして，選択できる手がなくなったら(相手がこの手を打ったら次の手がどうなるか分からないという状態に到達したら)それが葉(木の末端)となる。

終了時点のタイムステップをLとすると，各時間ステップt<Lで行動を以下式により選ぶ。

a_t = \text{argmax}_a \left( Q(s_t, a) + u(s_t, a) \right)

ここで，式中のu(s_t,a)は以下である。

u(s_t, a) = C_{\text{PUCT}} P(s, a) \frac{\sqrt{\sum_b N_r(s, b)}}{1 + N_r(s, a)}
分母がある状態におけるある行動をとった階数，分子がある状態においてとった行動回数の総和となるため，訪問回数の多い行動のu(s_t,a)は小さくなる。また，行動aの事前確率が大きい場合はその行動をとる確率が大きくなる(比例する)。
この項は，PUCTアルゴリズムに基づくボーナス項であり，多く訪問した手については採用確率を低くし，広い探索を促進する役割がある。
展開(expansion):

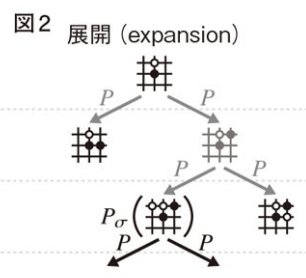
訪問回数が閾値を超えたら，sから行動選択した結果の状態s'を探索木に追加する。
評価(evaluation):

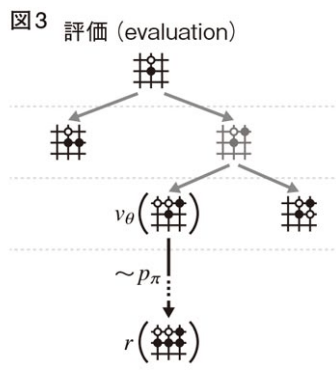
葉を2つの方法で評価する。1つ目は価値ネットワークによる評価，2つ目はロールアウトによる評価である。ロールアウトの時間ステップt≧Lでは双方のプレイヤーの行動はロールアウト方策p_{\pi}(a|s)(MCTSで使われる特定の戦略を指す)を使って選択する。

ゲームが終わったら報酬z_t=r(s_T)を計算する。r(s_T)は最終タイムステップTにおける報酬であり，勝ったら1，負けたら-1である。
記録(backup):

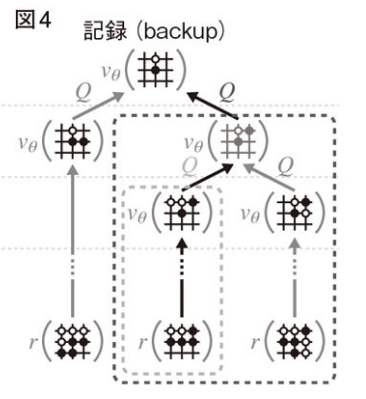
時間ステップt≦Lではロールアウトの統計をあたかもn_{rl}回負けたかのように更新しておく。

報酬が-1なため，W_r(s,a)が訪問回数分マイナスされている。
これにより，並列で走っている計算が同じノードをシミュレートする可能性を下げることができる。なぜなら低評価のノードはあまり良くない選択肢として扱われるため，並列に動いている他のプロセスもそのノードを選ぶ確率が低くなりそのノードをシミュレーションする可能性が下がるため。

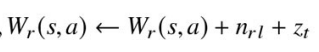
次に，末端の葉に到達して1回のシミュレーションが終了した時点で各時間ステップt≦Lの統計量に対してn_{rl}回の負けを元に戻し，ロールアウトの統計量を以下の通り更新する。

次に価値ネットワークの出力を使って，各時間ステップt≦Lの価値関数の統計量を以下の通り更新する。

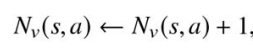
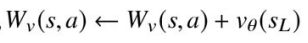
現在の状態sで行動aが選ばれているため＋1している。累積報酬に対して，価値ネットワークの出力v_{θ}(s_L)を追加している。これは葉ノードで価値ネットワークが予測した価値を累積報酬に反映させることを意味している。
各状態・各行動の評価値Q(s,a)はモンテカルロ平均とし，以下で計算される。

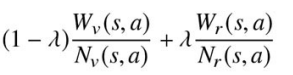
以上の1-4の操作が終われば再びルートからシミュレーションを繰り返す。AlphaGoは与えられた時間内でシミュレーションを繰り返し，探索が終了したら，ルートノードから最も訪問回数の多い行動を次の指し手として採用する(理由:その行動が他の行動に比べて多くシミュレーションされ，より信頼できると判断されるから)。

項目	メインネットワーク (Online Network)	ターゲットネットワーク (Target Network)
役割	各状態に対するQ値を計算し、行動を決定する	ターゲットQ値を計算し、Q学習の更新式で利用する
更新頻度	毎ステップで更新される	数千ステップor1エピソードごとにメインネットワークの重みをコピーして更新
目的	エージェントの行動選択やQ値予測	Q値のターゲット値を計算し、学習の安定性を保つ
重みの更新方法	勾配降下法で損失関数を最小化する	定期的にメインネットワークの重みをコピーして更新