Object Detection Learning Record
Link: https://www.sciencedirect.com/science/article/abs/pii/S0925231224008737



2017年-2020年:
- 2017年にマルチスケールのコンテキスト情報を得るための特徴ピラミッド構造(FPN)が提案され,ネットワークのbackboneに導入したRetinaNetは小物体の検出精度が効果的に向上する。
中でもResNet-101-FPNをbackboneに用いたネットワークのAP_s - YOLOv3だと全般的にRetinaNetに精度で勝つことができていない。
- CornerNetとCenterNetので使用されているbackboneはHourglassである(これは人間のポーズ推定タスクに使用されていたもの)。
- これは,各種類の砂時計ブロックを複数積み重ねて構成されている。各ブロックにはアップサンプリングとダウンサンプリング操作があり,異なるレベルの特徴マップ情報を取り込み,入力サイズにマッチしたヒートマップを出力することができる。
- Hourglassは異なるサイズの画像に柔軟に対応できるようになるが計算量も大きくなり,モデルの推論速度に影響し,必要なリソースも多くなる。
- 学習データ量が不足していたり,データの分布が一様でない場合にはオーバーフィット現象が起こりやすい。
- FCOSは4つの異なるbackboneネットワークを使用している(それが上の図の結果)。異なるbacknoneがネットワークモデルの検出精度に異なる結果をもたらす。
- BackboneによってCenterNetに勝ってたり勝ってなかったりする。
- アンカーボックスベースの手法はfeature map上の各点にn個のサンプルを計算するが,FCOSは1個のサンプルとして計算するため,サンプル数を劇的に少なくすることにより学習速度の向上も望める。
- HRNetは異なる解像度の特徴マップを計算でき,高解像度画像の特徴情報を保持することで詳細情報をよりよくとらえることができる。しかし,複数の解像度の画像を処理する必要があるため計算量が比較的多くなる。
- FPSはアンカーベースに勝っていないかも?(論文に表記がない)
- YOLOv4はクロスステージパーシャル(CSP)構造を含むようにbackboneネットワークを更新した。CSP接続により異なるレイヤーの特徴マップが相互に作用し,ネットワークが改善されより詳細な特徴情報を捉えることができるようになった。精度は向上したが計算量は大きくなり,推論速度に影響が出る。ちなみにアンカーベースの手法。
- CSPNetはDenseNetの改良版。安価なGPUで高速に動作することを念頭に改良したもの。計算量を10~20%削減し,精度を向上させることができた。シンプルに入力の特徴マップをチャンネル方向2つに分割して,片方だけDenseblockと同様に変換してもう片方はそのまま保持することで計算を減らしている。Resnetにも適用可能。※以下の(a)はDenseNetと同様

- PANを採用(FPNの改良版)

- CIoU lossを利用している。
- Bag of specials: 推論コストを少しだけ挙げて物体検知精度を大幅に上げる手法
- CSPNetはDenseNetの改良版。安価なGPUで高速に動作することを念頭に改良したもの。計算量を10~20%削減し,精度を向上させることができた。シンプルに入力の特徴マップをチャンネル方向2つに分割して,片方だけDenseblockと同様に変換してもう片方はそのまま保持することで計算を減らしている。Resnetにも適用可能。※以下の(a)はDenseNetと同様
各論での調査内容
アンカーボックスベースの物体検出の課題
- 事前設定するハイパーパラメータ数: フィーチャーマップ毎にアンカーボックスのハイパラ(アスペクト比など)を調整する必要があり,これが検出精度に影響を与えがち。
- ポジティブサンプル数とネガティブサンプル数の不均衡: アンカーボックスを使った手法だと,例えば画像中に約9000個程度のアンカーボックスがある場合にその中にポジティブサンプル(物体)は少ししかなく,大半がネガティブサンプル(背景)になる。FocalLossなどの対策はあるが,Lossを使用した微修正のため,不均衡問題を抜本的に解決しているわけではない。

FCOSとCenterNetの違い
FCOS(Fully Convolutional One-Stage Object Detection)とCenterNet(Objects as Points)は、どちらもアンカーボックスを使用しない物体検出モデルですが、設計思想や予測の方法が異なります。それぞれの特徴と違いを詳しく説明します。
1. FCOS(Fully Convolutional One-Stage Object Detection)
特徴
-
アンカーボックスを使用しない
- 物体検出において、従来のFaster R-CNNやRetinaNetのようなアンカーベースの手法とは異なり、FCOSは各ピクセル位置で直接バウンディングボックスを回帰する。
-
FPN(Feature Pyramid Network)を利用
- 画像の異なるスケールで予測を行うため、FPNを用いて多段階の特徴マップから物体を検出。
-
センターポイントを中心としたバウンディングボックス回帰
- 画像の各ピクセルを物体の候補点(センターポイント)とみなし、そのピクセルから左右上下の距離(距離エンコーディング)を学習しバウンディングボックスを構築。
-
分類・位置回帰・センターネスの3つのヘッド
- FCOSの出力は3つのブランチで構成される:
- クラス分類ヘッド:物体のクラスを予測
- 距離回帰ヘッド:各ピクセルからバウンディングボックスの4方向の距離(左・右・上・下)を回帰
- センターネスヘッド(Center-ness Score):物体の中心に近いほどスコアを高くすることで、検出精度を向上させる
- FCOSの出力は3つのブランチで構成される:
2. CenterNet(Objects as Points)
特徴
-
物体の中心点を直接予測
- FCOSが各ピクセルを基準に物体のバウンディングボックスを回帰するのに対し、CenterNetは物体の中心点を検出し、その点からバウンディングボックスのサイズを予測。
-
ヒートマップベースのアプローチ
- 物体の中心点をガウスヒートマップとしてエンコードし、ピーク(最も強い反応のある点)を中心としてバウンディングボックスを生成。
-
3つの出力
- ヒートマップ:物体の中心点の確率を表す
- オフセット:中心点が量子化(整数化)された誤差を補正
- サイズ回帰:物体の高さと幅を直接回帰
-
リアルタイム動作に向いた設計
- ヒートマップベースのシンプルな構造により、高速な推論が可能であり、リアルタイムアプリケーションに適している。
3. FCOSとCenterNetの主な違い
| 特徴 | FCOS | CenterNet |
|---|---|---|
| バウンディングボックスの生成方法 | ピクセルごとに左右上下の距離を回帰 | 物体の中心を検出し、そこからバウンディングボックスのサイズを回帰 |
| 中心点の扱い | Center-nessスコアで中心点を強調 | ヒートマップで物体の中心点を明示的に学習 |
| 出力 | クラス分類 + 距離回帰 + センターネス | ヒートマップ + オフセット + サイズ回帰 |
| FPNの利用 | あり(異なるスケールの特徴を利用) | なし(単一の特徴マップで予測) |
| 適用用途 | 高精度な物体検出 | 高速でリアルタイムな物体検出 |
| リアルタイム性 | 比較的高速だがCenterNetより遅い | より高速で軽量 |
| 学習の安定性 | 回帰が多いため学習が難しい | ヒートマップにより学習が安定しやすい |
4. どちらを選ぶべきか?
-
高精度な検出が求められる場合:
- FCOSの方が細かい物体の検出精度が高くなる傾向があるため、精度を優先するタスクには向いている。
-
リアルタイム処理が必要な場合:
- CenterNetの方が計算コストが低く、軽量なモデルで推論速度が速いため、リアルタイム処理が求められるアプリケーション(自動運転、監視カメラなど)に向いている。
-
小さい物体を検出したい場合:
- FPNを用いるFCOSは小さな物体の検出能力が高い。一方、CenterNetはヒートマップに依存するため、小さな物体の中心がぼやけてしまい、検出しにくくなる。
5. まとめ
| 項目 | FCOS | CenterNet |
|---|---|---|
| アンカーボックス | 不要 | 不要 |
| 特徴マップの活用 | FPNを使用 | シングルスケール |
| バウンディングボックスの生成方法 | 左右上下の距離回帰 | 物体の中心点を予測し、そこからサイズを推定 |
| 学習の安定性 | 回帰タスクが多いため難しい | ヒートマップで学習が安定しやすい |
| 推論速度 | 高速だがCenterNetより遅い | 非常に高速(リアルタイム向け) |
| 小さい物体の検出 | 得意(FPNによる高解像度特徴) | 苦手(ヒートマップがぼやけやすい) |
どちらのモデルもアンカーフリーでありながら、高速かつ高精度な物体検出を可能にしています。用途に応じて適切なモデルを選択してください。
参考サイト
- Hourglassの詳細:
- ConerNetの記事:
- CenterNet記事:
- FCOSの記事:
- YOLOv4の記事:


2021年-2024年:
- YOLOX(2021年): coupled detection headが物体の検出精度を損なう可能性があるとしてアンカーフリーのアプローチを導入。既存のcoupled detection headを切り離し,2つのブランチを用いて分類と回帰タスクを行う
- YOLOv5と比べてパラメータの増加を最小限に抑えながらモデルの検出能力を高めている。
- YOLOXのモデルアーキテクチャはかなり単純明快。そのため理解と実装を容易にする。
参考文献
Link: https://ieeexplore.ieee.org/abstract/document/10103630
Intro
- Few-shot object detection: FSODはターゲットドメインにおける新しいカテゴリの少数の物体インスタンスから学習することを目的としている。
- FSODは以下図に示すように第一段階で豊富な公開データに対して事前学習を行った後,わずかな注釈付きインスタンスで新規の物体を検出することを目的としている。

-
Problem Definition:
- K-shotの物体検出タスクは
C_novel - N-Way Object DetectionはN個の新規カテゴリの物体を検出するモデル。Nは
C_{novel} -
D_{novel} - 一般的なアプローチとしては以下である。
- 分類データで事前訓練されたBackboneを備えた最初の検出器モデル
M_{init} -
M_{init} D_{base} - 新規カテゴリ
C_{novel} D_{finetune} M_{base} M_{final}


- 分類データで事前訓練されたBackboneを備えた最初の検出器モデル
- K-shotの物体検出タスクは
Related Work
Relation Networks for Object Detection
Object Relation Module
Link: https://arxiv.org/abs/1711.11575

- Relation Moduleが挟まっている(点線部分)。これが新規開発のモジュール
- このモジュールは可変長の入力をとり,並列に実行可能かつ完全に微分可能(並列に実行可能なのはattentionと同様)。また入力と出力の間で次元が変化しないため,どのようなアーキテクチャでも柔軟に使用できる基本的な構成要素として機能する。
- 以上Figに示すように「インスタンス認識」「重複除去」のステップの学習に適用される。
- 一組の物体は個々に認識されるのではなく,同時に処理され,推論され,互いに影響しあう。

- このモジュールは,広い意味で(1)式に示すベーシックなattention moduleに類似しているが,物体検出に有効な形に変換している。以下詳しい説明。

- オブジェクトの関係性を表す特徴量
f_{R}(n) f_{A} f_{G} - 他のオブジェクトmの外観特徴
f^{m}_{A} W_v V \omega^{mn}

- 先の(2)式の影響度の重み
\omega^{mn} exp(\omega^{A}_{mn}) -
\omega^{A}_{mn} \omega^{G}_{mn}

- 先の(3)式にあった外観特徴重み
\omega^{A}_{mn} - ここにある
dot - この論文中でオリジナルの特徴量
f^{m}_{A} f^{n}_{A} d_{k}
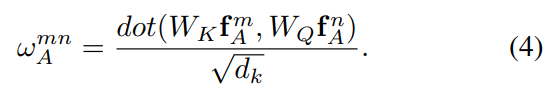
- 先の(3)式にあった幾何学的重みは(5)式で表される。これによりオブジェクト間の位置関係を考慮した関係重みが求まる。
-
\epsilon_{G}(f^{m}_{G},f^{n}_{G}) W_G - maxはReLU。

- 幾何学的特徴
f_{G} - さらにこの4次元ベクトルはFourier-based positional encodingにより異なる波長のsin/cos関数にエンコードする。これにより幾何学的特徴がよりリッチになる。


- 先の(3)式にあった外観特徴重み
- 最後に各オブジェクトnに対して,オブジェクトの関係性を表す特徴量
f_{R}(n) N_r -
f_{R}(n) f^{m}_{A} \frac{1}{N_r}

Relation for Duplicate Removal

- NMSを使ったヒューリスティックな方法はスコアの高いオブジェクトの近くにあるスコアの低い物体を消去する枠組みであるが,greedy approachと手動選択したパラメータにより明らかに最適な結果ではない。
- NMSの代わりに学習可能なRelation Moduleを用いた重複削除手法を提案。この手法は重複削除を「2クラス分類問題」として定式化する(ネットワーク処理の概要は上図)。
- 入力は検出されたオブジェクトのセット(以下に示す出力,つまりproposalされたインスタンスをRoIプーリングしたもの)。各オブジェクトには最終的な1024次元の特徴,分類スコア
s_0 s_1 s_{0}×s_{1}


- ネットワークは3つのステップをとる。
- 1024次元の特徴と分類スコアが融合されて外観特徴が生成。(多分図の
f^n - Relation Moduleが全ての外観特徴を変換する。
- 各オブジェクトの変換された特徴が線形分類器(上図(b)の
W_s s_1
- 1024次元の特徴と分類スコアが融合されて外観特徴が生成。(多分図の
- Rank feature(上図のrank embed箇所)について:
- スコアをランクに変換することが最も効果的なため,入力されたN個のオブジェクトがスコアの降順にソートされ,書くオブジェクトは対応するランク(
\in[1,N] - rank featureと元の1024次元の外観特徴の両方はそれぞれ図(b)の
W_{fR} W_{f}
- スコアをランクに変換することが最も効果的なため,入力されたN個のオブジェクトがスコアの降順にソートされ,書くオブジェクトは対応するランク(
【実装】Relation Network for Object Detection
以下のコードは、MXNet のシンボリック API で実装された multi‐head attention モジュール(およびその NMS 用バージョン)の処理内容を、TensorFlow(tf.keras を用いた実装例)で再現したものです。
以下では、各処理の意図と変換内容について解説しながら、サンプルコードを示します。
【処理内容の解説】
1. 基本の考え方
-
入力特徴量 (roi_feat) の変換
各 RoI(Region of Interest)の特徴量に対して、まず線形変換(Dense 層)を行い「query(Q)」や「key(K)」を得ます。
また、同じ特徴量(もしくはその一部)を「value(V)」として用います。 -
位置情報の活用
対となる RoI 同士の相対的な位置情報(position_embedding や position_mat)に対して 1×1 畳み込み(もしくは Dense 層)や活性化(ReLU)を適用し、位置に基づく重み(aff_weight)を算出します。
この重みは、後に注意スコア(affinity)の対数項として加えられ、幾何学的な近さなどを反映します。 -
Multi-head の処理
全体の次元(dim)を複数の head(group 個)に分割して計算します。
それぞれの head ごとに Q と K の内積を計算し、スケーリング後に位置情報から得た対数項を加算、Softmax を適用して正規化します。 -
出力の生成
正規化した注意重みと Value を掛け合わせ(行列積)、その後グループごとの 1×1 畳み込み(グループ畳み込み)で出力次元を調整します。
2. 「attention_module_multi_head」関数
この関数は、以下の処理を行います。
-
入力選択
-
roi_feat: shape [num_rois, feat_dim] -
position_embedding: shape [1, emb_dim, num_rois, nongt_dim](※MXNet は NCHW 形式) - もし
non_gt_indexが指定されていれば,tf.gather で対象行のみ抽出します。
-
-
位置特徴の変換
- 1×1 畳み込み層(Conv2D, data_format="channels_first")で位置埋め込みを fc_dim チャネルに変換し,ReLU を適用。
- 転置・reshape により、最終的に形状 [num_rois, fc_dim, nongt_dim] の位置重みを得る。
-
Query・Key の生成&分割
- roi_feat から Dense 層で query を生成し,group 個に分割(reshape + transpose)して形状 [group, num_rois, dim_group[0]] に。
- 同様に,non-gt 対象の roi_feat から key を生成し,形状 [group, nongt_num, dim_group[1]] に変換します。
-
Attention スコアの計算
- 各 head ごとに batch_dot(tf.matmul)で内積を取り,スケール(1/sqrt(dim_group))して,先の位置重みの対数項と足し合わせます。
- 転置・reshape を行い,softmax を適用して正規化。
-
Value と重みの積・出力層
- 得られた注意重みと Value(non-gt roi_feat)との行列積を取り,reshape 後にグループ付き 1×1 畳み込みを適用して最終出力を生成します。
3. 「attention_module_nms_multi_head」関数
こちらは、NMS(Non-Maximum Suppression)の代替として重複削除に利用する attention モジュールです。
主な違いは以下です。
-
roi_feat の shape が [num_rois, num_fg_classes, feat_dim] となっており,まずクラス軸と RoI 軸を入れ替え、平坦化します。
-
位置行列 (position_mat) からペアごとの位置埋め込みを抽出します。
(ここでは補助関数extract_pairwise_multi_position_embeddingを用いていますが,実際は論文中の手法に沿ったエンコーディングを実装してください) -
クエリ・キーの計算、multi-head 分割,attention の計算は上記とほぼ同様です。
ただし,各クラスごとに注意重みを計算し,最終的に出力形状を [num_rois, num_fg_classes, dim[2]] としています。
【TensorFlow での実装例】
以下に、上記の処理を再現したサンプルコードを示します。
※ なお,TensorFlow のバージョン 2.x(tf.keras.layers.Conv2D の groups 引数利用)を前提としています。
また,extract_pairwise_multi_position_embedding は簡易なスタブ関数として実装しています。
import tensorflow as tf
import math
# ===== 補助関数 =====
def extract_pairwise_multi_position_embedding(position_mat, emb_dim):
"""
【スタブ】ペアごとの位置埋め込みを抽出する関数。
position_mat: [num_fg_classes, num_rois, num_rois, 4]
emb_dim: 出力チャネル数(ここでは fc_dim[0] と同じ)
※実際の実装では論文の記述に従った埋め込み処理を行う
"""
# 例として、各位置情報 (4次元) に対して Dense 層で emb_dim 次元に変換する
dense_layer = tf.keras.layers.Dense(units=emb_dim, name='pairwise_pos_embedding')
# 入力をフラット化して処理後、元の形状に戻す
shape = tf.shape(position_mat)
num_fg = shape[0]
num_rois = shape[1]
pos_reshaped = tf.reshape(position_mat, [-1, 4])
embedded = dense_layer(pos_reshaped)
embedded = tf.reshape(embedded, [num_fg, num_rois, num_rois, emb_dim])
return embedded
# ===== attention_module_multi_head =====
def attention_module_multi_head(roi_feat, position_embedding, non_gt_index,
fc_dim, feat_dim,
dim=(1024, 1024, 1024), group=16, index=1):
"""
Multi-head attention モジュール(通常版)
Args:
roi_feat: Tensor of shape [num_rois, feat_dim]
position_embedding: Tensor of shape [1, emb_dim, num_rois, nongt_dim] (NCHW形式)
non_gt_index: インデックス(None の場合は全 RoI を使用)
fc_dim: 整数(通常 group と同じ値)
feat_dim: roi_feat の次元(dim[2] と同じである必要がある)
dim: (query_dim, key_dim, output_dim) のタプル
group: head の数
index: 識別用の番号(ネットワーク内での命名用)
Returns:
output: Tensor of shape [num_rois, dim[2]]
"""
# 各 head ごとの次元
dim_group = (dim[0] // group, dim[1] // group, dim[2] // group)
# non_gt_index が指定されていれば対象 RoI を抽出
if non_gt_index is None:
nongt_roi_feat = roi_feat
else:
nongt_roi_feat = tf.gather(roi_feat, non_gt_index, axis=0)
# ----- 位置特徴の変換 -----
# position_embedding: [1, emb_dim, num_rois, nongt_dim](NCHW)
conv_layer = tf.keras.layers.Conv2D(filters=fc_dim, kernel_size=(1,1), strides=(1,1),
padding='valid', data_format="channels_first",
name='pair_pos_fc1_' + str(index))
position_feat_1 = conv_layer(position_embedding) # → [1, fc_dim, num_rois, nongt_dim]
position_feat_1_relu = tf.nn.relu(position_feat_1)
# 転置して [num_rois, fc_dim, nongt_dim, 1] にし、最後の次元を squeeze
aff_weight = tf.transpose(position_feat_1_relu, perm=[2, 1, 3, 0])
aff_weight = tf.squeeze(aff_weight, axis=-1) # → [num_rois, fc_dim, nongt_dim]
# ----- Multi-head のための Query, Key の生成 -----
# Query: roi_feat から Dense 層で変換 → [num_rois, dim[0]]
query_dense = tf.keras.layers.Dense(units=dim[0], name='query_' + str(index))
q_data = query_dense(roi_feat)
# reshape: [num_rois, group, dim_group[0]] → 転置して [group, num_rois, dim_group[0]]
q_data_batch = tf.reshape(q_data, [-1, group, dim_group[0]])
q_data_batch = tf.transpose(q_data_batch, perm=[1, 0, 2])
# Key: nongt_roi_feat から Dense 層で変換 → [num_nongt, dim[1]]
key_dense = tf.keras.layers.Dense(units=dim[1], name='key_' + str(index))
k_data = key_dense(nongt_roi_feat)
k_data_batch = tf.reshape(k_data, [-1, group, dim_group[1]])
k_data_batch = tf.transpose(k_data_batch, perm=[1, 0, 2])
# Value: nongt_roi_feat(変換なし)
v_data = nongt_roi_feat # shape: [num_nongt, feat_dim]
# ----- Attention 計算 -----
# 各 head ごとに Q と K の内積(batch_dot)を計算
aff = tf.matmul(q_data_batch, k_data_batch, transpose_b=True) # → [group, num_rois, nongt_dim]
aff_scale = aff / math.sqrt(dim_group[1])
# 転置して [num_rois, group, nongt_dim]
aff_scale = tf.transpose(aff_scale, perm=[1, 0, 2])
# fc_dim と group は同じ値である前提
weighted_aff = tf.math.log(tf.maximum(aff_weight, 1e-6)) + aff_scale # [num_rois, fc_dim, nongt_dim]
aff_softmax = tf.nn.softmax(weighted_aff, axis=2)
# reshape: [num_rois * fc_dim, nongt_dim]
num_rois = tf.shape(roi_feat)[0]
aff_softmax_reshape = tf.reshape(aff_softmax, [num_rois * fc_dim, -1])
# Value と掛け合わせる: → [num_rois * fc_dim, feat_dim]
output_t = tf.matmul(aff_softmax_reshape, v_data)
# reshape → [num_rois, fc_dim * feat_dim, 1, 1]
output_t = tf.reshape(output_t, [num_rois, fc_dim * feat_dim, 1, 1])
# ----- 出力層:グループ付き 1x1 畳み込み -----
conv_linear = tf.keras.layers.Conv2D(filters=dim[2], kernel_size=(1,1),
groups=fc_dim, data_format="channels_first",
name='linear_out_' + str(index))
linear_out = conv_linear(output_t)
output = tf.reshape(linear_out, [num_rois, dim[2]])
return output
# ===== attention_module_nms_multi_head =====
def attention_module_nms_multi_head(roi_feat, position_mat, num_rois,
dim=(1024, 1024, 1024), fc_dim=(64, 16),
feat_dim=1024, group=16, index=1):
"""
NMS 用 Multi-head attention モジュール
Args:
roi_feat: Tensor of shape [num_rois, num_fg_classes, feat_dim]
position_mat: Tensor of shape [num_fg_classes, num_rois, num_rois, 4]
num_rois: RoI 数
dim: (query_dim, key_dim, output_dim)
fc_dim: タプル(例: (64, 16)); fc_dim[1] は group と一致すべき
feat_dim: roi_feat の次元
group: head の数
index: ネットワーク内での識別番号
Returns:
output: Tensor of shape [num_rois, num_fg_classes, dim[2]]
aff_softmax: 計算された attention 重み(後で解析等に利用可能)
"""
# 各 head ごとの次元
dim_group = (dim[0] // group, dim[1] // group, dim[2] // group)
# roi_feat: [num_rois, num_fg_classes, feat_dim] → 転置して [num_fg_classes, num_rois, feat_dim]
roi_feat = tf.transpose(roi_feat, perm=[1, 0, 2])
# 平坦化: [num_fg_classes * num_rois, feat_dim]
roi_feat_reshape = tf.reshape(roi_feat, [-1, feat_dim])
# ----- 位置埋め込み -----
# 補助関数を用いて,position_mat から [num_fg_classes, num_rois, num_rois, fc_dim[0]] の埋め込みを得る
position_embedding = extract_pairwise_multi_position_embedding(position_mat, fc_dim[0])
# 平坦化: [num_fg_classes * num_rois * num_rois, fc_dim[0]]
position_embedding_reshape = tf.reshape(position_embedding, [-1, fc_dim[0]])
# FullyConnected 層で変換 → [num_fg_classes * num_rois * num_rois, fc_dim[1]]
fc_layer = tf.keras.layers.Dense(units=fc_dim[1], name='nms_pair_pos_fc1_' + str(index))
position_feat_1 = fc_layer(position_embedding_reshape)
# reshape → [num_fg_classes, num_rois, num_rois, fc_dim[1]]
position_feat_1 = tf.reshape(position_feat_1, [-1, num_rois, num_rois, fc_dim[1]])
aff_weight = tf.nn.relu(position_feat_1)
# 転置して → [num_fg_classes, fc_dim[1], num_rois, num_rois]
aff_weight = tf.transpose(aff_weight, perm=[0, 3, 1, 2])
# ----- Multi-head attention の計算(クエリ・キー) -----
# Query: roi_feat_reshape から Dense 層で → [num_fg_classes*num_rois, dim[0]]
q_dense = tf.keras.layers.Dense(units=dim[0], name='nms_query_' + str(index))
q_data = q_dense(roi_feat_reshape)
# reshape → [num_fg_classes, num_rois, group, dim_group[0]] → 転置して [num_fg_classes, group, num_rois, dim_group[0]]
q_data_batch = tf.reshape(q_data, [-1, num_rois, group, dim_group[0]])
q_data_batch = tf.transpose(q_data_batch, perm=[0, 2, 1, 3])
# 平坦化: [num_fg_classes * group, num_rois, dim_group[0]]
q_data_batch = tf.reshape(q_data_batch, [-1, num_rois, dim_group[0]])
# Key: 同様に
k_dense = tf.keras.layers.Dense(units=dim[1], name='nms_key_' + str(index))
k_data = k_dense(roi_feat_reshape)
k_data_batch = tf.reshape(k_data, [-1, num_rois, group, dim_group[1]])
k_data_batch = tf.transpose(k_data_batch, perm=[0, 2, 1, 3])
k_data_batch = tf.reshape(k_data_batch, [-1, num_rois, dim_group[1]])
# Value: roi_feat([num_fg_classes, num_rois, feat_dim])
v_data = roi_feat
# ----- Attention スコア計算 -----
aff = tf.matmul(q_data_batch, k_data_batch, transpose_b=True) # → [num_fg_classes * group, num_rois, num_rois]
aff_scale = aff / math.sqrt(dim_group[1])
# aff_weight の形状は [num_fg_classes, fc_dim[1], num_rois, num_rois] で,
# 平坦化して [num_fg_classes * fc_dim[1], num_rois, num_rois]
aff_weight_reshape = tf.reshape(aff_weight, [-1, num_rois, num_rois])
weighted_aff = tf.math.log(tf.maximum(aff_weight_reshape, 1e-6)) + aff_scale
aff_softmax = tf.nn.softmax(weighted_aff, axis=2)
# reshape: [num_fg_classes, fc_dim[1] * num_rois, num_rois]
# ※ fc_dim[1] == group と仮定
num_fg = tf.shape(aff_weight)[0]
aff_softmax_reshape = tf.reshape(aff_softmax, [num_fg, fc_dim[1] * num_rois, num_rois])
# ----- 出力生成 -----
# batch_dot: [num_fg_classes, fc_dim[1]*num_rois, feat_dim]
output_t = tf.matmul(aff_softmax_reshape, v_data)
# reshape → [num_fg_classes, fc_dim[1], num_rois, feat_dim]
output_t_reshape = tf.reshape(output_t, [-1, fc_dim[1], num_rois, feat_dim])
# 転置して → [fc_dim[1], feat_dim, num_rois, num_fg_classes]
output_t_reshape = tf.transpose(output_t_reshape, perm=[1, 3, 2, 0])
# reshape → [1, fc_dim[1]*feat_dim, num_rois, num_fg_classes]
output_t_reshape = tf.reshape(output_t_reshape, [1, fc_dim[1] * feat_dim, num_rois, -1])
# グループ付き 1×1 畳み込み(groups=fc_dim[1])
conv_linear = tf.keras.layers.Conv2D(filters=dim[2], kernel_size=(1,1),
groups=fc_dim[1], data_format="channels_first",
name='nms_linear_out_' + str(index))
linear_out = conv_linear(output_t_reshape)
# reshape: [dim[2], num_rois, num_fg_classes] → 転置して [num_rois, num_fg_classes, dim[2]]
linear_out_reshape = tf.reshape(linear_out, [dim[2], num_rois, -1])
output = tf.transpose(linear_out_reshape, perm=[1, 2, 0])
return output, aff_softmax
【まとめ】
- 上記のコードは、MXNet の各シンボリック演算(Convolution, FullyConnected, batch_dot, Reshape, Transpose, Softmax など)を TensorFlow の tf.keras.layers や tf.reshape / tf.transpose / tf.matmul で再現しています。
- 入力データの形状(特に NCHW 形式の場合)に注意しながら,data_format="channels_first" を指定してグループ畳み込みなども実装しています。
- また,attention_module_nms_multi_head では,ペアごとの位置埋め込みを抽出する処理を補助関数として用意しており,実際の論文の実装に合わせる場合はこの部分の詳細実装が必要です。
このように、各工程を理解した上で TensorFlow 版に書き換えることで、MXNet で実装された手法と同等の動作を実現できます。