Open10
[読書メモ]関数型プログラミングの基礎(ISBN: 978-4-86594-059-6)
ピン留めされたアイテム
本を読むモチベーション
- 関数型プログラミングを前から習得したいと思っていた
- 関数型プログラミングを習得するメリットが短く言語化されていて勉強するモチベーションが上がった
- JavaScriptで関数型プログラミングの基礎を解説している本があってちょうどよかった
- 慣れていない言語で入門すると、文法などに気を取られて本来勉強したいことへの関心が薄れてしまうため
2章 なぜ関数型プログラミングが重要か?
関数型プログラミングの特徴
- 関数を言語の最も基本的な要素として扱う(ファーストクラスオブジェクトとしての関数)
- 参照透過性を確保できること
ファーストクラスオブジェクトとしての関数
- ファーストクラスオブジェクト: 計算の対象となる「値」を意味する
- 数値や文字列は代表的なファーストクラスオブジェクト
- 関数がファーストクラスであるとは、次の性質をもつ
- 関数を変数にバインドする
- 関数をデータ構造に埋め込む
- 関数適用の際に関数を引数として渡す
- 関数から関数を返す
// 1. 関数を変数にバインドできる const succ = (n: number): number => { return n +1; }; // 2.関数をデータ構造に埋め込む const hoge = { add: (n: number, m: number): number => { return n + m; } }; // 関数がファーストクラスオブジェクトであることの利点は高階関数が利用できること // 高階関数とは、関数を引数で受け取ったり、関数を返すことができる関数を意味する const sum = (array: number[]): number => { let result = 0; // 3. 関数適用の際に関数を引数として渡す // (item) => {...}は関数 array.forEach((item: number): void => { result += result + item; }); return result; } // 4. 関数から関数を返す const adder = (n: number) => { return (m: number): number => { return n + m; } }
参照透過性
- (簡単に言うと)プログラムの構成要素が同じもの同士は等しい
- 値の参照透過性
- 変数の参照透過性
- 関数の参照透過性
- 同じ引数で何度実行されても同じ値を返すこと
- TypeScriptの配列は可変なデータ構造の1つ
// 可変なデータが参照透過性を破壊する例 const array: number[] = [1]; console.log(`${array}`); array.push(2); console.log(`${array}`); // 変数名は同じであるが、中身が変更されている - 代入は参照透過性を破壊する
// 代入によってコンテキストが変化し、参照透過性を破壊する let x = 1; succ(x); // この時点では2が返される x = 2; succ(x); // この時点では3が返される - 入出力を伴う関数には参照透過性がない。入出力が処理系にとって隠れたコンテキストとして振る舞うから。
参照透過性を保証する
-
値の参照透過性を保証する(可変なデータの排除)
// 関数を用いてオブジェクト型のようなデータ構造を不変なデータとして実装した例 // 関数は一度作成されれば、その内部は変更できない不変なデータとみなせる。 // Obj 型を定義して、オブジェクト型のようなデータ構造を不変なデータとして扱う。 type Obj = (key: string) => any; const empty: Obj = (_) => { return null; }; const get = (key: string, obj: Obj) => { return obj(key); }; const set = (key: string, value: any, obj: Obj): Obj => { return (key2: string) => { if (key === key2) { return value; } else { return get(key2, obj); } }; }; const obj1 = set("name", "Alice", empty); const obj2 = set("age", 30, obj1); const obj3 = set("email", "alice@example.com", obj2); console.log(get("name", obj3)); // "Alice" console.log(get("age", obj3)); // 30 console.log(get("email", obj3)); // "alice@example.com" console.log(get("hobby", obj3)); // undefined -
変数の参照透過性を保証する(代入の排除)
// 代入を排除した足し算 const add = (x: number, y: number): number => { if (y == 0) { return x; } else { return add(x + 1, y - 1); } }; -
関数の参照透過性を保証する(副作用の分離)
// 副作用が分離できていないコード // 副作用を分離するためには現在の時刻というテキストを関数の外に出す必要がある const age = (birthYear: number): number => { const currentYear: number = new Date().getFullYear(); const age: number = currentYear - birthYear; return age; };- 副作用を分離するためのより柔軟な手法はモナドです。モナドは高階関数を使ってコンテキストをカプセル化する。特に、副作用の根源である入力値をIOもなどでカプセル化すると、副作用を持つ関数を組み合わせてより複雑な入出力を作り上げることが可能になる。
関数型プログラミングの利点
-
コードのモジュール性が高まる
- 後で書く
- 関数適用
- 関数合成
- 関数による遅延評価
- コードの一部の計算が後回しにされる評価の方法
-
コードのテストを容易にする
- 副作用のある部分と純粋な関数を分離することで、純粋な関数についてはユニットテストなどで挙動を確認することができる。
-
コードの正しさを証明できる
-
succ(0) + succ(x)とsucc(succ(x))が等しいことを推論(この文脈では等式変換)で数学的に証明できる。 - 証明するものが複雑な場合やルールが多いときは、人間の直感が必要になる。単体テストを書くのは容易だが、挙動を確認できるのは組み合わせの一部だけである。
- 推論による数学的な証明にも、ユニットテストにも長所と短所がある。両者のバランスを取る方法として、プロパティテストがある。これは大量のテストケースを自動生成し、コードが一定の性質(= 仕様)を保っているかどうかを確認する。さまざまなプログラミング言語でプロパティテストのライブラリが実装されている。
-
3章 心の準備
DRY原則
- 見た目が簡潔になる
- 汎用的なコードになる
- メンテナンスを容易にする
- 開発時間を短縮する
// countの回数分、funを適用する関数
const times = (count: number, arg: number, memo: number, fun: (n: number, m: number) => number): number => {
if (count > 1) {
return times(count - 1, arg, fun(arg, memo), fun);
} else {
return fun(arg, memo);
}
};
const add = (n: number, m: number): number => {
return n + m;
};
// nとmは自然数とする
// 掛け算はn * m = n + n + ... + n (m回続く)
const multiply = (n: number, m: number): number => {
return times(m, n, 0, add);
};
// nとmは自然数とする
// 冪乗はn^m = n * n * ... * n (m回続く)
const exponential = (n: number, m: number): number => {
return times(m, n, 1, multiply);
};
// multiply(10, 2) => times(2, 10, 0, add) => times(1, 10, add(10, 0), add)
// => times(1, 10, 10, add) => times(0, 10, add(10, 10), add)
// => add(10 ,10)
console.log(multiply(10, 2));
// exponential(10, 2) => times(2, 10, 1, exponential) => times(1, 10, multiply(10, 1), multiply)
// => times(1, 10, 10, multiply) => => times(0, 10, multiply(10, 10), multiply) => multiply(10, 10)
console.log(exponential(10, 2));
抽象化への指向
- 抽象化によって、人間の認知負荷を避ける
-
arrayのreduce関数は関数を渡すだけで処理を簡潔に記述できる
// 挙動を確認するためにいろいろ出力している
const sum = (array: number[]): number => {
return array.reduce((previousValue: number, currentValue: number, currentIndex: number, array: number[]) => {
console.log(`currentIndex: ${currentIndex}, previousValue: ${previousValue}, currentValue: ${currentValue}`);
return previousValue * currentValue;
});
}
console.log(sum([1, 2, 3]));
セマンティクスを意識する
- プログラムという目に見えるコードが実行されている背後に、セマンティクスをいう見えない領域が隠されている。
5章 プログラムをコントロールする仕組み (1/2)
TypeScriptのif文
- TSのif文はファーストクラスオブジェクトとしての関数ではない。つまり、
const hoge = if(...)のような書き方ができない。if文のように評価されても値を返すことのないものを、**文(statement)**と呼ぶ。一方で、評価されると値を返すものは、**式(expression)**と呼ぶ。HaskellやScalaなどの関数型言語ではif分は式として定義されている。
代数的データ構造とパターンマッチ
- リストは
empty()で表現される空のリストかcons(value, kist)で表現される空でないリストで表現できるので、代数的データ構造となっている。 - サンプルコードのメモ
-
empty()やcons(value, list)は無名関数を返す。 -
match(data, pattern)のdataは((pattern: Pattern) => any)の無名関数となっている。つまり、dataは関数で、引数にpatternを渡せる。data(pattern)はempty()やcons(value, list)でそれぞれ実装されている。empty()ではPatternクラスのempty()メソッドを実行し、cons(value, list)ではPatternクラスのcons()メソッドを実行するように実装されている。 - リストは
empty()やcons(3, cons(2, cons(1, empty())))(空のリストに数値を追加していくようなイメージ)のようにして実現できる。
-
// リストを代数的データ構造として実装する ※便宜上、数値型の型のリストとする
// リストはempty()で表現される空のリスト or cons(value, list)で表現される空でないリストのいずれになる
type Empty = () => ((pattern: Pattern) => any); // NOTE: Pattern型のempty()メソッドの返り値の型に依存する
type Cons = (value: number, list: (pattern: Pattern) => any) => ((pattern: Pattern) => any);
type List = ReturnType<Empty> | ReturnType<Cons>;
type Pattern = {
empty: () => any, // NOTE: 実装メソッドによって返り値の方が異なる
cons: (head: number, tail: List) => any // NOTE: 実装メソッドによって返り値の方が異なる
};
// 空のリスト (pattern)を引数とした関数を返す
const empty: Empty = () => {
// キーが各データ構造の名前、値がそのデータ構造に対応した処理であるオブジェクト型のインスタンスが渡される
return (pattern: Pattern) => {
// Pattern型のクラスはemptyとconsメソッドを持つので、empty()メソッドを呼び出す。
return pattern.empty();
};
};
// 空でないリスト (pattern)を引数とした関数を返す
const cons: Cons = (value: number, list: List) => {
return (pattern: Pattern) => {
// Pattern型のクラスはemptyとconsメソッドを持つので、cons()メソッドを呼び出す。
return pattern.cons(value, list);
};
};
// 代数的データ型に対してパターンマッチを実現する関数
// dataには代数的データ(Pattern型の引数を受け付ける関数の型を指定する)、patternにはオブジェクト型のインスタンスが入る
const match = (data: ReturnType<Empty> | ReturnType<Cons>, pattern: Pattern) => {
return data(pattern);
};
// 引数alistに渡されたリストが空のリストかどうか判定する
const isEmpty = (alist: List): boolean => {
return match(alist, {
empty: () => {
return true;
},
cons: (head, tail) => {
return false;
}
});
};
// 引数alistに渡されたリストの先頭の要素を返す
const head = (alist: List): number | null => {
return match(alist, {
empty: () => {
return null;
},
cons: (head, tail) => {
return head;
}
});
};
// 引数alistに渡されたリストの末尾の要素(=先頭を取り除いた要素)を返す
const tail = (alist: List): List => {
return match(alist, {
empty: () => {
return empty();
},
cons: (head, tail) => {
return tail;
}
});
};
// こんな使い方をする
const emptyList = empty();
// [1]というリストを作りたい時
const list1 = cons(1, empty())
// [1, 2]というリストを作りたい時
const list2 = cons(2, list1)
// リストが空かどうか確かめる
console.log(`expected: true, result: ${isEmpty(empty())}`);
console.log(`expected: false, ${isEmpty(list2)}`);
console.log(`expected: null, ${head(empty())}`);
console.log(`expected: 2, ${head(list2)}`);
console.log(`expected: 1, ${head(tail(list2))}`);
再帰による反復処理
- 関数が自身を呼び出すことで、反復処理を実現できる。
- ただし、終了条件と終了条件に近づくように、再帰呼び出しの引数を設計する必要がある。
- 上のリストの例では、リストの後には必ずリストが入り、末尾には
empty()が入るようになっており、再帰的なデータ構造となっている。再帰的な構造になっている場合は、数学的帰納法で数学的にプログラムの動きを保証することができる。
// NOTE: 上の続き
const len = (alist: List): number => {
return match(alist, {
empty: () => {
return 0;
},
cons: (head, tail) => {
return 1 + len(tail);
}
})
};
console.log(`expected: 0, ${len(emptyList)}`);
console.log(`expected: 2, ${len(list2)}`);
# 5章 プログラムをコントロールする仕組み (2/2)
- 数式も再起的なデータ構造なので書いてみる
// 自然数の足し算と掛け算を代数的データ構造で実現する
type Pattern = {
num: (n: number) => number
add: (exp1: Exp, exp2: Exp) => number,
mul: (exp1: Exp, exp2: Exp) => number,
};
type Exp = ((pattern: Pattern) => any);
type Num = (n: number) => Exp;
type Add = (exp1: Exp, exp2: Exp) => Exp;
type Mul = (exp1: Exp, exp2: Exp) => Exp;
const num: Num = (n: number) => {
return (pattern: Pattern) => {
return pattern.num(n);
};
};
const add: Add = (exp1: Exp, exp2: Exp) => {
return (pattern: Pattern) => {
return pattern.add(exp1, exp2);
};
};
const mul: Mul = (exp1: Exp, exp2: Exp) => {
return (pattern: Pattern) => {
return pattern.mul(exp1, exp2);
};
};
const match = (data: Exp, pattern: Pattern) => {
return data(pattern);
};
const calc = (exp: Exp): number => {
return match(exp, {
num: (n) => {
return n;
},
add: (expL, expR) => {
return calc(expL) + calc(expR); // 再帰的に処理をする
},
mul: (expL, expR) => {
return calc(expL) * calc(expR); // 再帰的に処理をする
}
});
}
console.log(`excepted:2 , result: ${calc(num(2))}`);
console.log(`excepted:3 , result: ${calc(add(num(1), num(2)))}`);
console.log(`excepted:6 , result: ${calc(mul(num(2), num(3)))}`);
console.log(`excepted:21 , result: ${calc(mul(add(num(1), num(2)), add(num(3), num(4))))}`);
6章 関数を利用する
関数の評価戦略
- 関数の適用の際に引数を直ちに評価する方法を正格評価という。一方、引数の評価が後回しにされる方法を遅延評価という。JavaScriptは正格評価なので、以下のコードは無限ループして1を返さない。Haskellなどの遅延評価を採用している言語は無限ループせず、1を返す。
const left(x, y) => {
return x;
}
const infiniteLoop = ( ) => {
return infiniteLoop();
}
left(1, infiniteLoop())
- JavaScriptでも関数を使い実行のタイミングを制御することで遅延評価をすることができる。
- 掛け算では0 * n = 0となるので、第一引数が0の時は、第二引数を評価する必要がない。
// 掛け算の遅延評価
const lazyMultiply = (funX: (...args: any[]) => number, funY: (...args: any[]) => number) => {
const x = funX();
if (x === 0) {
return 0;
} else {
return x * funY();
}
}
const infiniteLoop = (): number => {
return infiniteLoop();
};
console.log(lazyMultiply(
() => {return 0},
infiniteLoop,
));
- 引数のない関数で値がラッピングされた構造を、サンク(thunk)と呼ぶ。
- サンクを使うことで遅延評価が実現できる。
サンクで無限を表現する
- 数学以外でも「いつ終了するか現時点ではわからない」といった性質のデータはたくさんある
- ユーザの入力やネットワークの応答など
-
ストリームと呼ばれるデータ型
- リスト型をサンクを使って拡張したもの
- ストリーム型のデータ構造:
STREAM[T] = empty() | cons(T, FUN[_ => STREAM[T]]) - リスト型のデータ構造:
STREAM[T] = empty() | cons(T, LIST[T]])
// サンクによるストリーム型の定義
type Stream = (pattern: Pattern) => any;
type TailThunk = () => Stream;
type Pattern = {
empty: () => null,
cons: (head: number, tailThunk: TailThunk ) => number | number[] | Stream;
};
const stream = {
empty: () => {
return (pattern: Pattern) => {
return pattern.empty();
}
},
cons: (head: number, tailThunk: any) => {
return (pattern: Pattern) => {
return pattern.cons(head, tailThunk);
}
},
match: (data: Stream, pattern: Pattern) => {
return data(pattern);
},
// 先頭の要素を取得する
head: (aStream: Stream): null | number => {
return stream.match(aStream, {
empty: () => { return null; },
cons: (value, tailThunk) => {
return value;
}
})
},
// 先頭を除いた要素を取得する
tail: (aStream: Stream) => {
return stream.match(aStream, {
empty: () => { return null; },
cons: (value, tailThunk) => {
return tailThunk(); // ここで初めてサンクを評価する
}
})
},
// streamからn個取得してリストで返す
take: (aStream: Stream, n: number): number[] => {
return stream.match(aStream, {
empty: () => { return null; },
cons: (value, tailThunk) => {
if (n === 0) {
return [];
} else {
return [value].concat(stream.take(tailThunk(), n-1));
}
}
});
}
};
const sample = stream.cons(1, () => { return stream.cons(2, () => { return stream.empty() })});
console.log(`expected: 1, result: ${stream.head(sample)}`);
console.log(`expected: null, result: ${stream.head(stream.empty())}`);
// 無限に1が続く数列
const ones = stream.cons(1, () => {
return ones;
});
// 無限に連続する整数列を生成する
const enumFrom = (n: number) => {
return stream.cons(n, () => {
return enumFrom(n + 1);
});
};
console.log(`expected: null, result: ${stream.take(stream.empty(), 10)}`);
console.log(`expected: 10, result: ${stream.take(ones, 10).length}`);
console.log(`expected: 10, result: ${stream.take(enumFrom(1), 10).length}`);
関数と参照透過性
- 関数における参照透過性とは、「ある関数が同じ引数で呼び出されていれば、必ず同じ値を返す」こと。
- つまり、「関数呼び出しの結果は、その関数の引数のみに依存する」
- 副作用を伴わずに参照透過性を持つ関数のことを、純粋な関数と呼ぶ。
- 副作用は関数から参照透過性を奪うものであるが、コンピュータプログラムにとって必要な要素である。
- 「状態」とは「時間の経過とともに変化する量」である。その状態を管理するためには、時間の経過を管理の対象に含めなければならない。関数型プログラミングでは、関数によって管理できる(モナドのこと => 7章で解説する)。
7章 高階関数を活用する
カリー化で関数を返す
- カリー化* => 複数の引数を持つ関数(多項関数)を一つだけの引数を持つ関数(一項関数)に変換すること。
// カリー化された関数
const multipleOf = (n: number) => {
return (m: number) => {
if (m % n === 0) {
return true;
} else {
return false;
}
}
};
console.log(`expected: true , result: ${multipleOf(2)(4)}`);
console.log(`expected: false, result: ${multipleOf(3)(4)}`);
multipleOf関数の簡約
multipleOf(2)(4)
=> {
return (m: number) => {
if (m % 2 === 0) {
return true;
} else {
return false;
}
}
}(4)
=> if (4 % 2 === 0) {
return true;
} else {
return false;
}
=> true
- **カリー化関数の最大の特徴は、引数を一部分だけの引数だけに適用できること。**カリー化関数を一部分に適用することを、部分適用という。
- 関数をパイプラインに見立てると、カリー化関数はパイプラインにパイプラインが入ったようなもの
- multipleOf(2)のように一部を適用した場合は、内部のパイプラインが押し出されるようなイメージで、適用されなかった内部の関数が返ってくる。
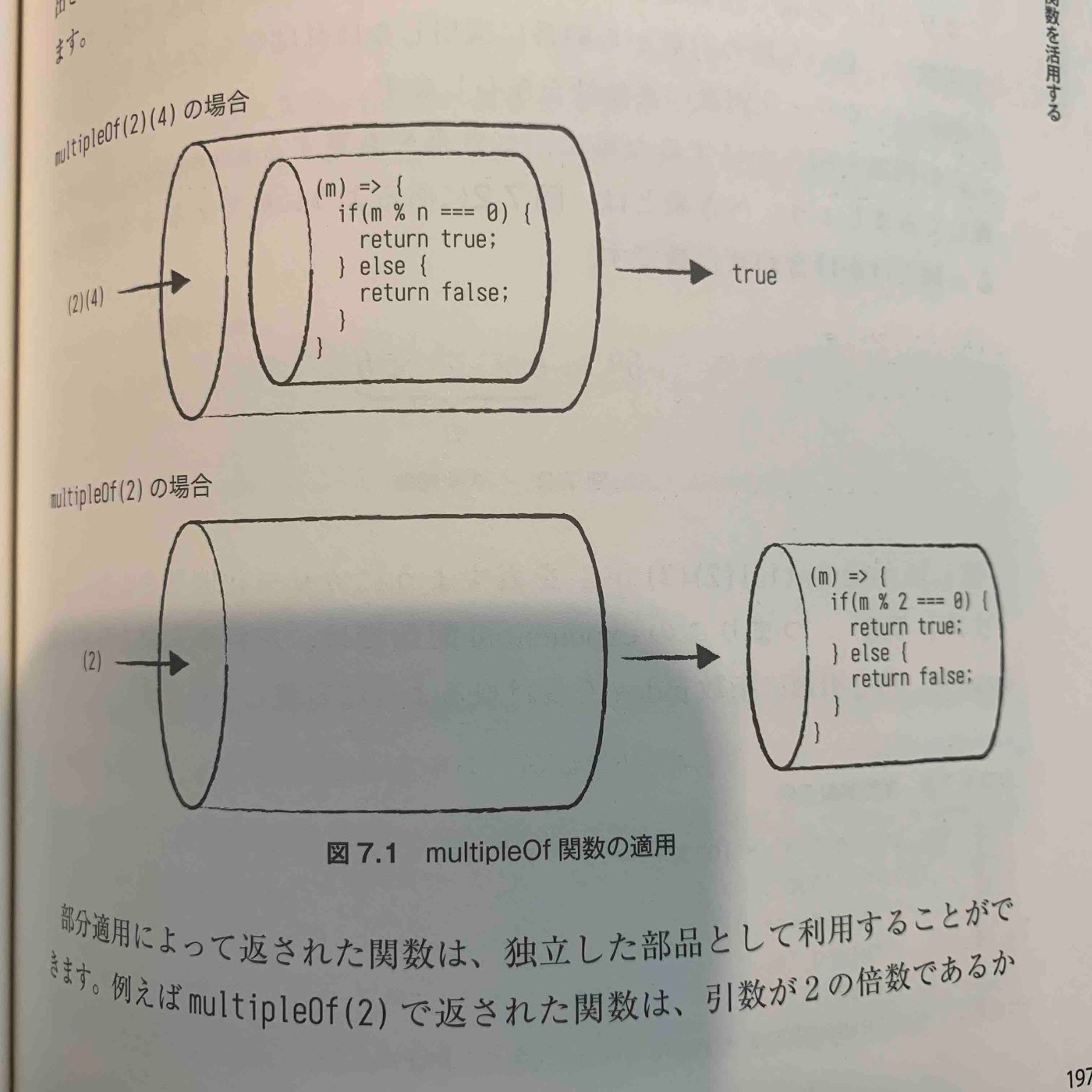
- カリー化の定義で注意すべき点は、**引数の順番である。カリー化関数は、必ず左側の引数から順番に適用しなければならない。**この制約はカリー化関数の柔軟性を左右する。
// baseのindex乗を計算するカリー化関数
const exponential = (base: number) => {
return (index: number): number => {
if (index === 0) {
return 1;
} else {
return base * exponential(base)(index - 1);
}
}
};
console.log(`expexted: 8, result: ${exponential(2)(3)}`);
// カリー化の引数を反転させる高階関数
const flip = <T1, T2> (fun: (x: T1) => ((y: T1) => T2)) => {
return (x: T1) => {
return (y: T1) => {
return fun(y)(x); // 部分適用する順番を逆転させる
}
}
};
const square = flip(exponential)(2);
const cube = flip(exponential)(3);
console.log(`expexted: 16, result: ${square(4)}`);
console.log(`expexted: 64, result: ${cube(4)}`);
チャーチ数
- ラムダ計算を発明したアロンゾ・チャーチはカリー化を多用することで、自然数を定義できることを示した。これをチャーチ数という。チャーチ数のアイデアは関数適用の回数によって数値を表現するもの。
succ(0); // 1を表現
succ(succ(succ(0))); // 3を表現
7章 高階関数を活用する
コンビネータで関数を組み合わせる
- flip関数はカリー化関数の引数を逆転させ、その部分適用によって新たな関数を生み出した。flip関数をのように関数を組み合わせるための高階関数を、(狭義の)コンビネータと呼ぶ。
// nが約数かどうか判定する関数
const multipleOf = (n: number) => {
return (m: number) => {
if (m % n === 0) {
return true;
} else {
return false;
}
}
};
const even = multipleOf(2);
// notコンビネータを作る
// const odd = not(even)のように使いたい
// evenは (m :number) => boolean という型になっている
const not = <T,> (fun: (x: T) => boolean ) => {
return (x: T) => {
return !fun(x);
}
};
const odd = not(even);
console.log(`expected: true , result: ${odd(3)}`);
console.log(`expected: false, result: ${odd(2)}`);
関数を合成する
// fとgを合成する関数 f(g(x))のようなイメージ
// fとgを合成するには、引数の数と型が一致している必要がある。また、g(x)の返り値の型はfの引数を一致している必要がある。
const compose = <T,>(f: (x: T) => T, g: (x: T) => T) => {
return (arg: T) => {
return f(g(arg));
}
};
const f = (x: number) => {
return x * x + 1;
};
const g = (x: number) => {
return x - 2;
};
console.log(`compose(f, g)(2): ${compose(f, g)(2)}, f(g(2)): ${f(g(2))}`);
関数合成による抽象化
- TODO: last関数(リストの末尾を取得する関数)がhead関数とreverse関数の関数合成で実現できるコードを書く。
// ast関数(リストの末尾を取得する関数)がhead関数とreverse関数の関数合成で実現できるコードを書く。
- 関数合成によってさまざまな関数を簡潔に定義できる
-
length(list)=>(sum•map(alwaysOne))(list)- 各要素を1にして、合計する
-
last(list)=>(head•reverse)(list)- リストを反転させて、先頭を取得する
-
7章 高階関数を活用する
クロージャーを使う
// 環境における変数のバインディング
const foo = 1; // 変数fooに数値1をバインドする
const bar = "string"; // 変数barに"string"をバインドする
- 環境の情報を
<foo |-> 1, bar |-> "string">のように表記する。このような環境のとき、変数fooを参照すると、fooに対応する値が取り出され、1という値に置換される。 - 関数適用と「環境」の関係は? => 関数が適用されると、仮引数と実引数の対応が新たな環境に追加される。例えば、
identity(1)を実行した場合は<any |-> 1>という内容の環境が作られる。 -
const twoFold = multipleOf(2);としたとき、部分適用によって<n |-> 2>という環境が作られる。ともに内側で定義された無名関数がtwoFoldにバインドされる。twoFoldについて無名関数の立場から見ると、借り引数のnは自由変数であるが、外側にある変数nを参照することができる。 - 定義された時点での環境を包み込んだ関数をクロージャーと呼ぶ*
クロージャーで状態をカプセル化する
- 下記の関数は内部にcountingNumberを持つ。外部から
countingNumberにアクセスする手段を持たない。しかし、関数が呼び出されるたびにcountingNumberが増えていく。=> このクロージャーは変化する状態を内部にカプセル化している。
const counter = (init: number) => {
let countingNumber = init;
return () => {
countingNumber = countingNumber + 1;
return countingNumber;
};
};
const counterFromZero = counter(0);
console.log(counterFromZero()); // 1が出力される
クロージャーで不変なデータ構造を作る
- クロージャーが状態をカプセル化する機能を利用して、不変なデータ構造を作ることができる。
// クロージャーを使って不変なデータ構造を作る
type Obj = (key: string) => any;
const object = {
empty: () => {
return null;
},
set: (key: string, value: any) => {
return (obj: Obj | null) => {
return (queryKey: string) => {
if (key === queryKey) {
return value;
} else {
return object.get(queryKey)(obj);
}
}
};
},
get: (key: string) => {
return (obj: Obj | null) => {
if (obj !== null) {
return obj(key);
} else {
return null;
}
};
}
};
const hoge = object.set("key", "value")(object.empty());
console.log(object.get("key")(hoge));
const robots = object.set("HAL9000", "2001: a space odessay")(object.set("C3PO", "Star Wars")(object.empty()));
console.log(object.get("HAL9000")(robots));
クロージャーでジェネレータを作る
TODO: 素数ジェネレータを作ることができる
クロージャーの純粋性
- クロージャーの内部の状態が不変か可変かどうかで純粋性(= 参照透過性)は異なる。
-
multipleOf()関数は内部の状態が不変なので純粋、一方counter()関数は内部の状態が呼び出すごとに変化するので純粋ではない。
-