JijModelingでフロー捕捉型配置問題を実装してみた

この記事はGENDA Advent Calendar 2025#3 および 数理最適化 Advent Calendar 2025の12日目の記事です。

はじめに

こんにちは、データサイエンティストのoddgaiです。私事ながら本日12/12は誕生日です。妻から欲しいものを聞かれたのですが何も思い浮かばず悲しくなりました。願うことはもはや家族の健康しかありません・・・

さて、施設配置問題は空間内において施設の望ましい配置場所を見つける問題で、最適化手法の適用対象の1つです。施設配置問題といえばp-メディアン問題やp-センター問題などが有名で、少し調べれば日本語の解説記事や実装例もいくつかヒットします。一方で、フロー捕捉型配置問題（Flow Capturing Location Problem: FCLP）^[1]は実務でも応用できそうなおもしろい問題なのですが、日本語の情報が論文くらいしか見当たりませんでした。

そこでこの記事では、FCLPの概要と定式化、そしてJijModelingによる実装例を紹介します。施設配置問題に興味がある方や、人流データを活用した出店戦略に関心がある方の参考になれば幸いです。

なお、FCLPの他にもFIP（Flow Interception Problem）やFILM（Flow Interception Location Model）など複数の呼び方がありますが、今回はFCLP（Flow Capturing Location Problem）で統一します。どなたか違いを教えてください！

問題設定

フロー捕捉型配置問題とは

フロー捕捉型配置問題（FCLP）は、ネットワーク上を移動する人々の流れ（フロー）に対して、なるべく多くのフローを捕捉できるように施設を配置する問題です。ここでいう「捕捉」とは、フローの経路上に何かしらの施設を配置することを表します。

以下の図で説明します。図のような街にコンビニを1店舗だけ出店させたいとします。矢印のように人が移動しているとき、どこに出店すればより多くの人に（寄り道なしで）利用してもらえるか？このような問題がFCLPです。この図くらいの規模であれば人間でも解けますが、もっと街が大きくなったり、人が増えたり、出店数が増えると人間では手が出せなくなりそうですね。

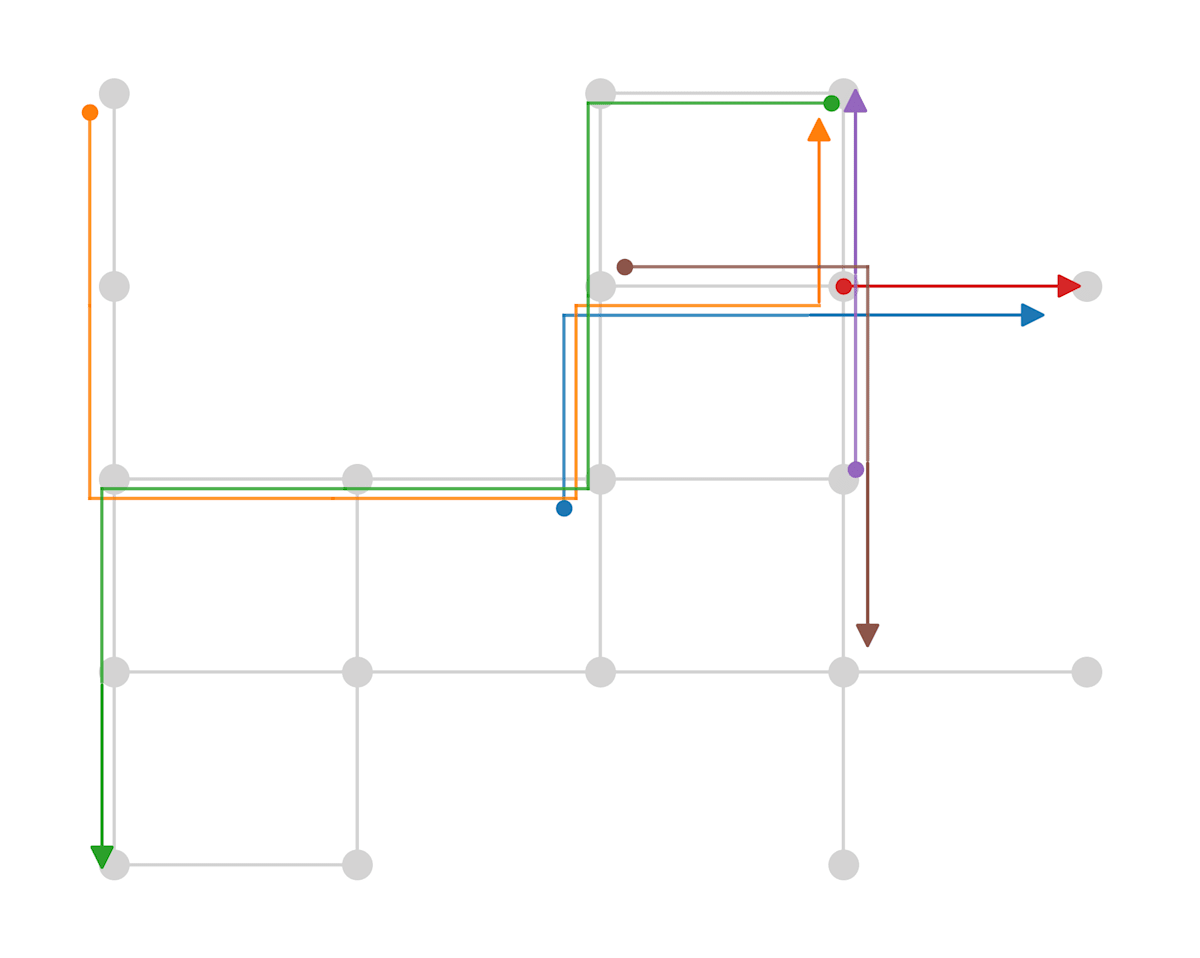
道路ネットワークとその上を移動するフロー

応用例

FCLPは以下のように様々な場面での活用が考えられます。イメージしやすいのはコンビニなどのふらっと立ち寄る系の施設ですが、検問所や防犯カメラなど何かを検知したい場面でも使えそうです。また物理的な対象だけではなく、テレビCMの放送スケジュールといった応用例も考えられています。

• コンビニ
• 宅配ロッカー
• ガソリンスタンド^[2]、充電ステーション
• 観光案内所
• 看板広告^[3]
• 検問所^[4]
• 防犯カメラ
• テレビCM^[5]

拡張モデル

今回紹介する基本モデルに加えて、以下のようにさまざまな拡張が研究されています。

• 広告などを想定し、捕捉回数が多いほど効果が高いと考えるモデル^[6]
• 施設を見逃すケースを考慮し、確率的に捕捉されると仮定したモデル^[7]
• 迂回して施設を利用することを許容するモデル^[8]

定式化

以下の定数を導入します。

• $Q: フローの集合$
• $K: 配置候補地点の集合$
• $p: 配置施設数$
• $f_q: フローq \in Q の流量$
• $a_{qk}: 地点k \in Kがフローqの経路上にあるとき1、そうでないとき0$

以下の0-1変数を導入します。

$$x_k = \begin{cases} 1 & 地点kに施設を配置する, \\ 0 & \text{otherwise,} \end{cases}$$

$$y_q = \begin{cases} 1 & フローqが捕捉される, \\ 0 & \text{otherwise.} \end{cases}$$

以上を用いると、FCLPは以下のような0-1整数計画問題として定式化できます。

$$\begin{align} \text{maximize} \quad & \sum_{q \in Q} f_q y_q \\ \text{subject to} \quad & \sum_{k \in K} x_k = p \\ & y_q \le \sum_{k \in K} a_{qk} x_k \qquad && \forall q \in Q \\ & x_k \in \{0,1\} \qquad && \forall k \in K \\ & y_q \in \{0,1\} \qquad && \forall q \in Q \end{align}$$

目的関数(1)は捕捉フロー量の総和を表し、これを最大化します。式(2)は$p$個の施設を配置することを表します。式(3)は、フロー$q$を捕捉するためにはフロー$q$の経路上に少なくとも1つは施設を配置する必要があることを意味します。式(4)と式(5)は変数$x_k$と$y_q$の0-1制約です。最適解では、多くのフローを重複なく効率的に捕捉するような施設配置が得られます。

数値実験

先ほどの図の規模であれば人間でも目星をつけられますが、ネットワークが大きくなったり、フロー数が増えたり、施設配置数が増えると手に負えなくなります。そこで数理最適化の出番です。

サンプルデータ

先ほどの図のネットワークを使います。これは格子状ネットワークからランダムにノード（頂点）を削除して作りました。

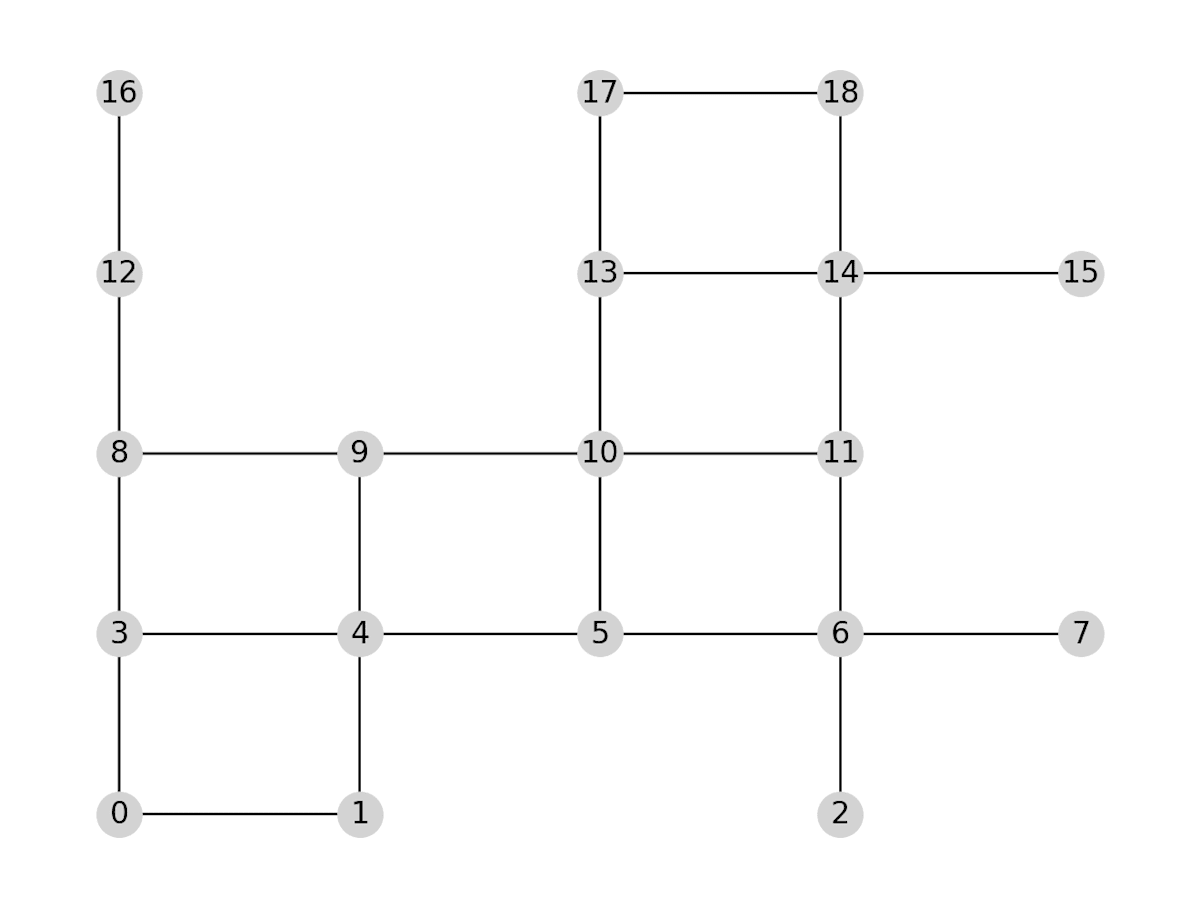
今回使う道路ネットワーク

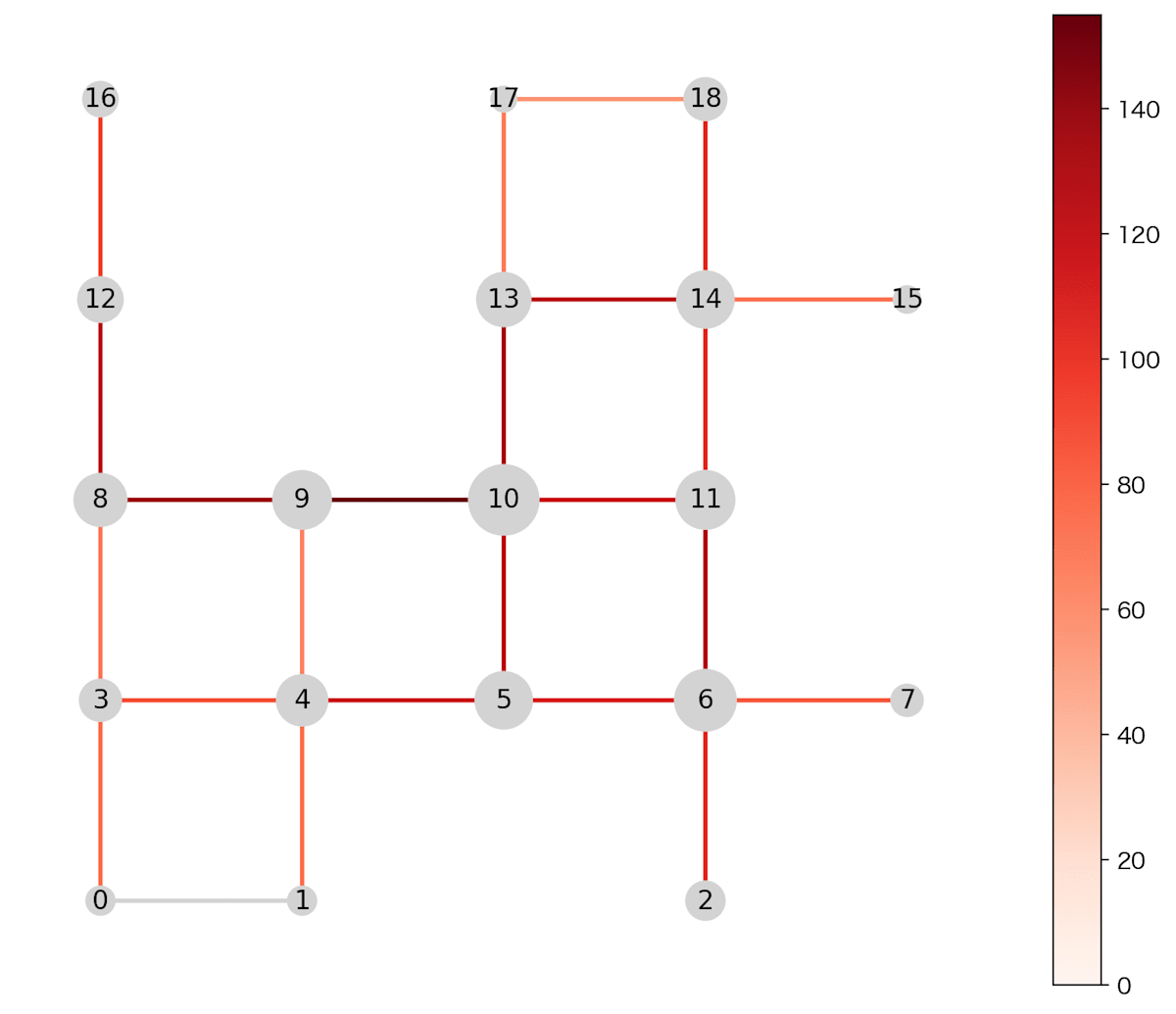
このネットワーク上にランダムなフローを流します。始点と終点をランダムに決めて、そこへランダムな流量を与えます。試しにランダムに100フロー（各フローの流量は1〜10）を流して可視化すると以下のようになりました。通過する流量に応じてノードの大きさとエッジの色を変えています。

この状況でどこに施設を配置するのがいいのか決めます。

ネットワーク生成コード

import random
import rustworkx as rx
from rustworkx.visualization import mpl_draw

def generate_road_like_network(
    rows: int,
    cols: int,
    p_remove_node: float,
    seed: int
):
    """
    rows x cols の格子状ネットワークを作り、そこからランダムにノードを削除する

    return:
        g: rx.PyGraph
        positions: dict[node_index] = (x, y)
    """
    random.seed(seed)

    # 削除しないノードを決定し、連番のインデックスを割り当てる
    grid_to_node = {}  # (r, c) -> node_index
    positions = {}
    node_idx = 0
    for r in range(rows):
        for c in range(cols):
            if random.random() >= p_remove_node:
                grid_to_node[(r, c)] = node_idx
                positions[node_idx] = (c, r)
                node_idx += 1

    # グラフを作成
    g = rx.PyGraph()
    g.add_nodes_from([None] * len(grid_to_node))

    # エッジを追加（両端が存在するもののみ）
    for (r, c), u in grid_to_node.items():
        if (r, c + 1) in grid_to_node:
            g.add_edge(u, grid_to_node[(r, c + 1)], {"length": 1})
        if (r + 1, c) in grid_to_node:
            g.add_edge(u, grid_to_node[(r + 1, c)], {"length": 1})

    return g, positions

g, positions = generate_road_like_network(rows=5, cols=5, p_remove_node=0.15, seed=8)
mpl_draw(g, positions, with_labels=True, node_color="lightgray")

フロー作成コード

ランダムなフロー作成

def generate_random_flows(
    g: rx.PyGraph,
    num_flows: int,
    min_amount: int = 1,
    max_amount: int = 10,
):
    """
    グラフ g 上でランダムな OD フローを num_flows 個つくる

    return:
      flows: list[dict]
    """
    flows = []
    nodes = list(g.node_indices())
    all_shortest_paths = rx.graph_all_pairs_dijkstra_shortest_paths(g, lambda e: e["length"])

    for _ in range(num_flows):
        s, t = random.sample(nodes, 2)
        amount = random.randint(min_amount, max_amount)
        flows.append({"source": s, "target": t, "path": all_shortest_paths[s][t], "amount": amount})

    return flows

flows = generate_random_flows(g, num_flows=100)

# a_example[q][k]: 頂点kがflows[q]のpath上に含まれるとき1、そうでないとき0をとる
a_example = []
for q, flow in enumerate(flows):
    a_example.append([])
    for k in g.node_indices():
        if k in flow["path"]:
            a_example[q].append(1)
        else:
            a_example[q].append(0)

フロー可視化コード

import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
from collections import defaultdict

def draw_flow_heatmap(graph, pos, flow_list):
    # 各ノードの通過フロー数をカウント
    node_counts = defaultdict(int)
    for fl in flow_list:
        for node in fl["path"]:
            node_counts[node] += fl["amount"]

    # 各エッジの通過フロー数をカウント
    edge_counts = defaultdict(int)
    for fl in flow_list:
        path = fl["path"]
        for i in range(len(path) - 1):
            u, v = path[i], path[i + 1]
            edge_key = (min(u, v), max(u, v))
            edge_counts[edge_key] += fl["amount"]

    max_node_count = max(node_counts.values()) if node_counts else 1
    max_edge_count = max(edge_counts.values()) if edge_counts else 1
    cmap = plt.cm.Reds

    # ノードの色とサイズをリストで作成
    node_colors = []
    node_sizes = []
    for node in graph.node_indices():
        count = node_counts.get(node, 0)
        intensity = count / max_node_count if count > 0 else 0
        node_colors.append("lightgray")
        node_sizes.append(10 + 1000 * intensity)

    # エッジの色をリストで作成
    edge_colors = []
    for u, v in graph.edge_list():
        edge_key = (min(u, v), max(u, v))
        count = edge_counts.get(edge_key, 0)
        intensity = count / max_edge_count if count > 0 else 0
        edge_colors.append(cmap(0.3 + 0.7 * intensity) if count > 0 else "lightgray")

    fig, ax = plt.subplots(figsize=(10, 8))
    mpl_draw(
        graph, pos,
        ax=ax,
        with_labels=True,
        node_color=node_colors,
        node_size=node_sizes,
        edge_color=edge_colors,
        width=2,
        font_color="black",
    )

    # カラーバーを追加
    norm = mcolors.Normalize(vmin=0, vmax=max_edge_count)
    sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
    sm.set_array([])
    cbar = fig.colorbar(sm, ax=ax)
    cbar.ax.yaxis.set_tick_params(color="black")
    cbar.ax.tick_params(labelcolor="black")

    return fig

draw_flow_heatmap(g, positions, flows)

モデル実装

先ほど定式化したものを実装します。モデラーはPuLPやPython-MIPなどいくつかありますが、今回はOptimization Night #11で紹介されていたJijModelingを使ってみます。

詳細な説明は公式のチュートリアルに譲りますが、JijModelingでは以下の手順で最適化問題を解きます。

• 最適化モデル実装
• モデルにデータを入力してインスタンスに変換
• インスタンスをソルバーで解く

まずは最適化モデルを実装していきます。

FCLPのモデル実装

import jijmodeling as jm

# パラメータ
p = jm.Placeholder("p", dtype=jm.DataType.INTEGER, description="配置施設数")
K = jm.Placeholder("K", dtype=jm.DataType.INTEGER, description="頂点数")
Q = jm.Placeholder("Q", dtype=jm.DataType.INTEGER, description="フロー数")

f = jm.Placeholder("f", dtype=jm.DataType.INTEGER, shape=(Q,), description="フローqの流量")
a = jm.Placeholder("a", dtype=jm.DataType.INTEGER, shape=(Q, K), description="頂点kがフローqの経路上に含まれるとき1、そうでないとき0")

# 決定変数
x = jm.BinaryVar("x", shape=(K,), description="頂点kに施設を配置するとき1、そうでないとき0")
y = jm.BinaryVar("y", shape=(Q, ), description="フローqが捕捉されるとき1、そうでないとき0")

# 添字
k = jm.Element("k", belong_to=(0, K))
q = jm.Element("q", belong_to=(0, Q))

# 定式化
problem = jm.Problem("FCLP", sense=jm.ProblemSense.MAXIMIZE)

## 目的関数: 捕捉流量を最大化
problem += jm.sum(q, f[q] * y[q])

## 制約式
problem += jm.Constraint("施設配置数", jm.sum(k, x[k]) == p)
problem += jm.Constraint("フロー捕捉", y[q] <= jm.sum(k, a[q, k] * x[k]), forall=q)

## ノートブックで実行すると数式表現が出せる
problem

JijModelingの機能で地味に便利だなと思ったのが、実装したモデルを以下のように数式として出力できることです。デバッグ時に役に立つのはもちろん、社内でのちょっとした共有にも使えそうです。最近では簡単なモデル実装をClaudeなどのAIにやってもらうケースもあると思いますが、その際のチェックにも重宝しそうです。またmarimoではこれを右クリックすればLatex記法がコピーできて、"理解ってるな"と思いました。

Jupyterやmarimoなどのノートブックだと数式表現を出せて便利！なんと右クリックでLatex記法がコピーできる

ちなみに、JijModelingは近日大幅なアップデートも予定されているようです。期待。

https://zenn.dev/jij_inc/articles/2025-12-09-jijmodeling2-a-new-code

データを入力してインスタンスに変換

次に、以下のようにモデルにデータを入力します。なおJijModelingにはランダムなデータを生成する機能もありましたが、今回は使いませんでした。

# サンプルデータセット
example_dataset = {
    "p": 2,
    "K": len(g.nodes()),
    "Q": len(flows),
    "f": [f["amount"] for f in flows],
    "a": a_example
}

# ランダムなデータを生成することもできる
# random_dataset = problem.generate_random_dataset(
#     options={
          # "p": 2,
          # "K": 10,
          # "Q": 10,
          # "f": range(1, 10),  # 1 ~ 9
          # "a": range(0, 2)  # 0 or 1
#     },
#     seed=123
# )

# モデルにデータを投入
example_instance = jm.Interpreter(example_dataset).eval_problem(problem)

ソルバー実行

最後にソルバーを実行します。JijModelingではOMMX Adapterというツールを介すことによって、インスタンスをさまざまなソルバーで解くことができます。Adapterの一覧はこちらにあり、SCIP / HiGHS / Gurobiといったメジャーなソルバーにも対応していそうです。今回はSCIPで解くのでOMMXPySCIPOptAdapterを使います。

ちなみに、今回くらいの規模（ノード数19, フロー数100, 配置施設数2〜7）であれば1インスタンスあたり4msくらいで解けました。

from ommx_pyscipopt_adapter import OMMXPySCIPOptAdapter

solution = OMMXPySCIPOptAdapter.solve(example_instance)

結果

まず、施設を1つ配置する場合は以下のような配置が最適解になりました。中心部にあって流量が多い9, 10あたりが選ばれそうだなと思ってましたが予想通りです。

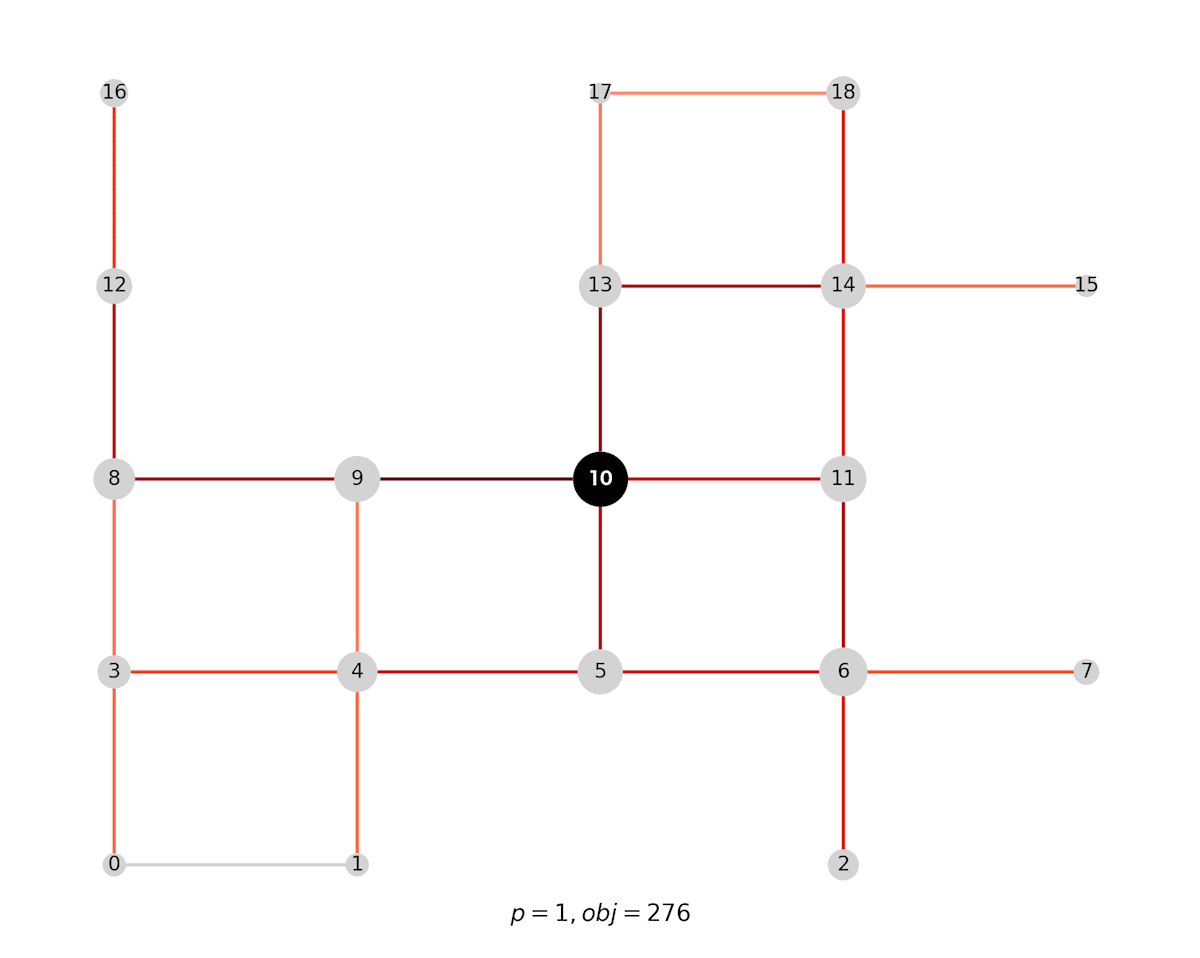
施設を1つ配置した場合の最適解。黒いノードが配置場所

次に、施設を2つ配置する場合は以下のような配置になりました。10の次に選ばれるのが6なのは少し意外に思えます。FCLPの基本モデルでは、1つのフローを1回捕捉しても複数回捕捉しても目的関数は変わらないため、なるべく多くのフローを重複なくカバーするような施設配置になります。

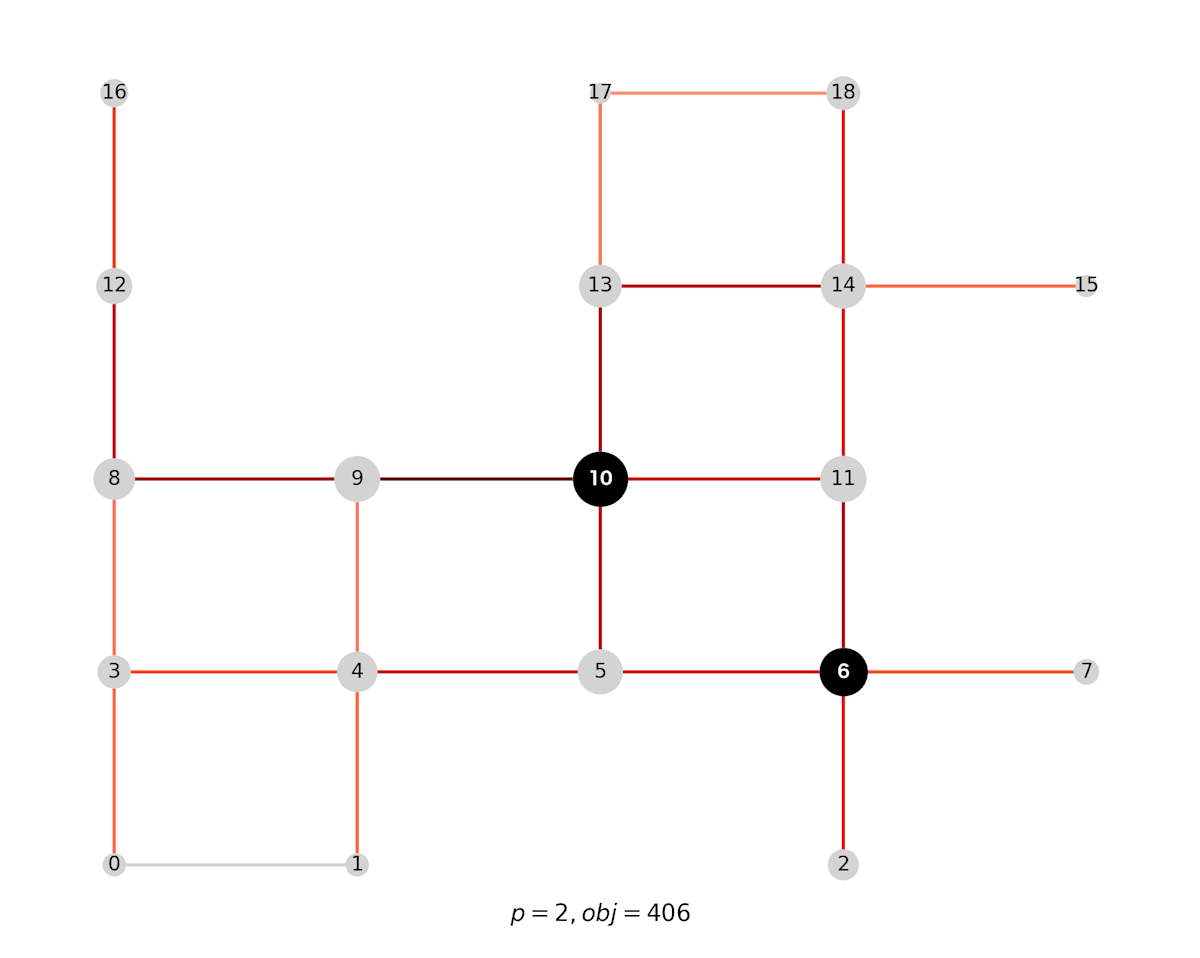
施設を2つ配置した場合の最適解

なお、このとき捕捉できた流量は406です。全フロー流量の合計は533なので、たった2つの施設で全体の約76%のフローをカバーできたことになります。

次に、配置施設数を変えたときにどれくらいフローを捕捉できるか見てみます。施設数を1から6まで変化させて最適化を実行し、捕捉流量をグラフにすると以下のようになります。

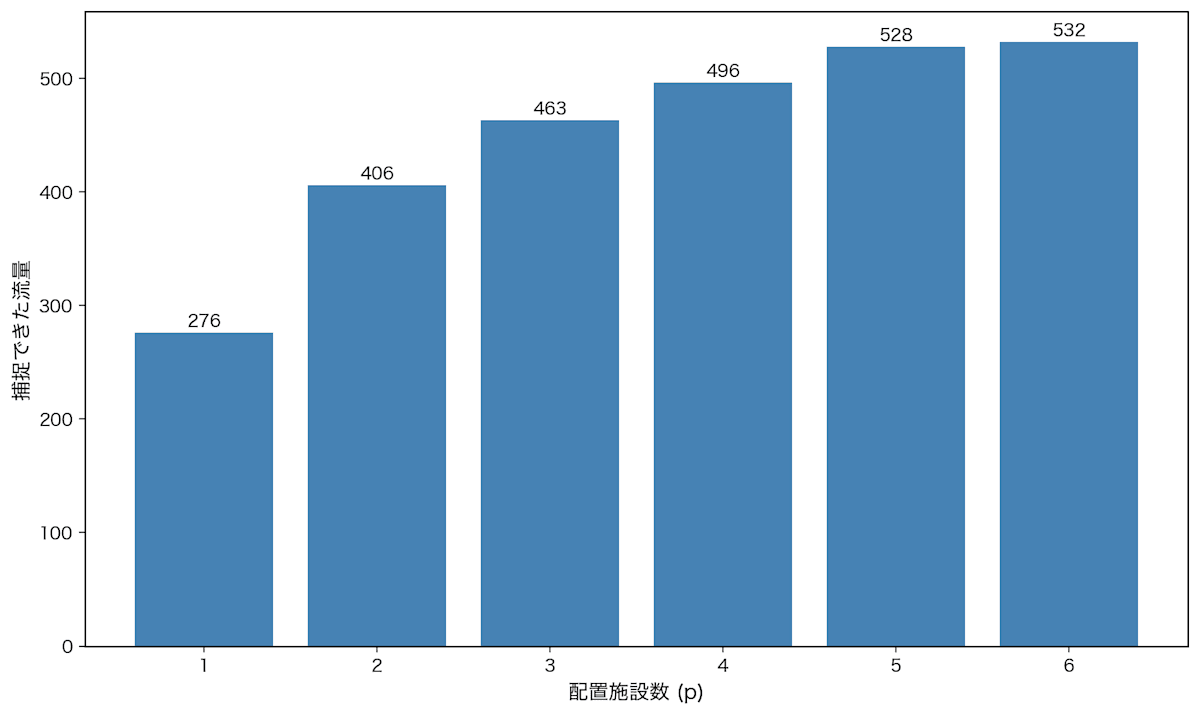
配置施設数と捕捉流量の関係

施設数が増えるほど捕捉流量も増えていますが、その増加率は徐々に小さくなっています。これは、最初の数個の施設で主要なフローを捕捉した後、追加の施設では残りの小さなフローしか捕捉できないためです。このグラフをみると$p=3, 4, 5$くらいがコスパの良い施設数な気がしますね。

最後に、施設数1から6までの配置結果を並べて可視化してみます。10 → 6 → 8 → 3 → ... のような順番で選ばれていくのはやはり直感に反しますが、これもフロー全体を効率的に捕捉しようとしている結果です。

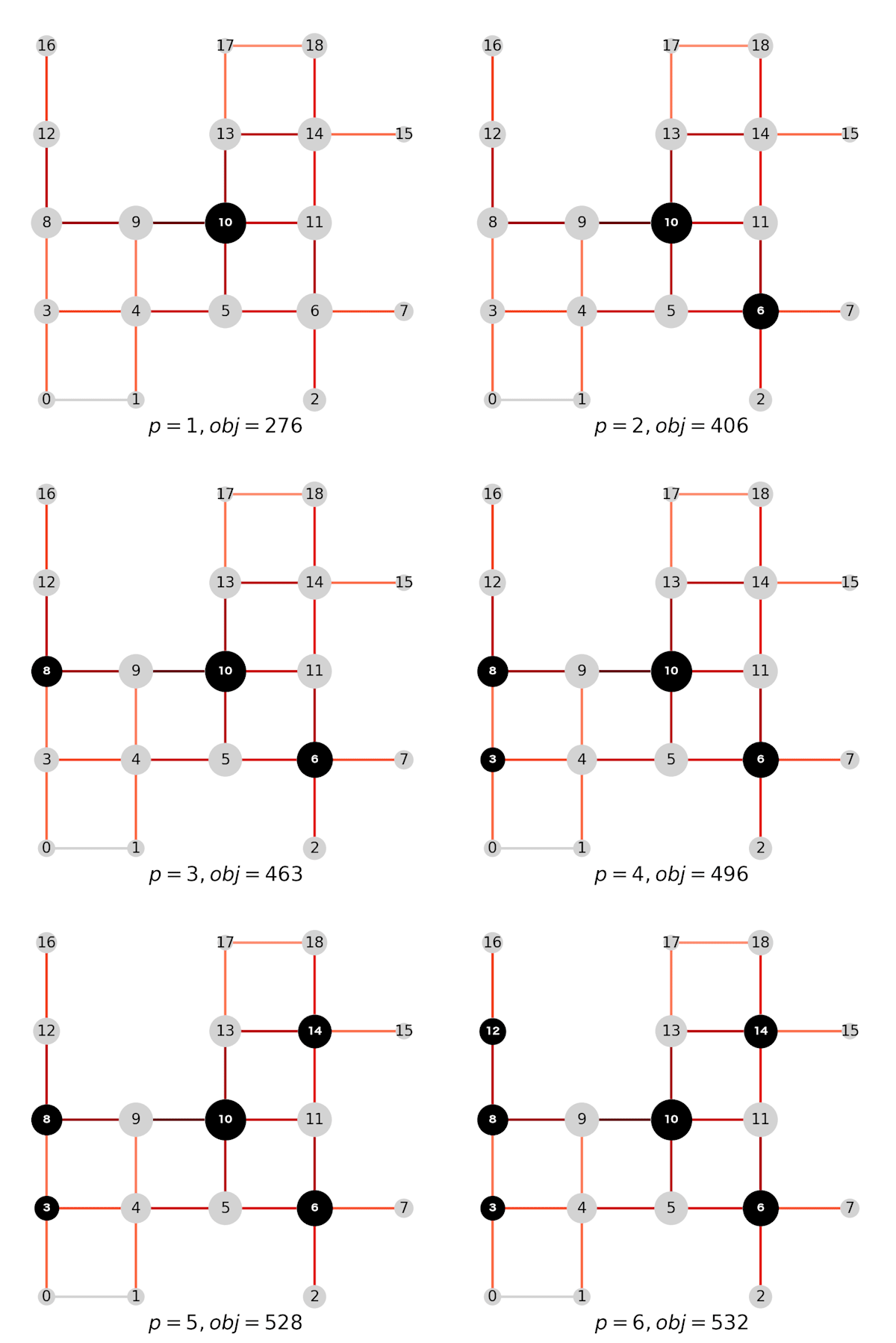
施設数を変えたときの最適配置

おわりに

この記事ではフロー捕捉型配置問題（FCLP）の概要、定式化、そしてJijModelingによる実装例を紹介しました。

近年はGPSなどから詳細な人流データが取得できるようになっているため、FCLPのような最適化モデルの実用性も高まっているのではないかと思っています。

今回は基本モデルを扱いましたが、実務では複数回捕捉や捕捉確率などの拡張を考慮することで、より現実的な問題に対応できるでしょう。興味を持った方はぜひ試してみてください！

脚注

1. Hodgson, M.J., A flow-capturing location-allocation model, Geographical Analysis, 22, pp.270-279, 1990.

2. M. Kuby and S. Lim, The flow-refueling location problem for alternative-fuel vehicles, Socio-Economic Planning Sciences, 39, pp.125–145, 2005.

3. M. J. Hodgson and O. Berman, A billboard location model, Geographical and Environment Modeling, 1, pp.25–45, 1997.

4. M. J. Hodgson, K. E. Rosing, and J. Zhang, Locating vehicle inspection stations to protect a transportation network, Geographical Analysis, 28, pp.299–314, 1996.

5. 小貝洸希，八尾優作，丹野一輝，濱田賢吾，田中健一， 栗田治 (2020): 複数回の広告接触を考慮した CMスケジューリング問題: 視聴パターンに着目したフロー捕捉型配置モデル，オペレーションズ・リサーチ, Vol. 65, pp.93–103, 2020.

6. M. J. Hodgson and O. Berman, A billboard location model, Geographical and Environment Modeling, 1, pp.25–45, 1997

7. 松尾太一朗，田中健一，栗田治，介在機会モデルを導入したフロー捕捉型配置問題，都市計画論文集，50, pp.622–627, 2015.

8. Berman, O., Bertsimas, D. and Larson, R.C. (1995): Locating discretionary service facilities, II: Maximizing market size, minimizing inconvenience, Transportation Science, Vol. 43, pp.623–632.