Zenn
🎮

円形の扇アニメーションをつくりたい

2024/01/17に公開
#
hlsl
#
spriteshader
#
三角比
#
高校生歓迎
tech

初めに.今から記事を見てくださる人へ

私自身、ゲーム系の専門学校現役生です。
周りや後輩と自分自身を比べたとき、
これはわかっておいてほしい！！！ っていうのがありましたし、
逆に 私はこれが苦手だな と思う部分があり必死に勉強してきました。

今回は後輩君が 円形の体力ゲージが作りたい と
Xでポストしていたのをきっかけに書いてみました。
内容自体は 高校生でもわかります。
数学がこんな風に使われるのか！を知って、勉強のモチベーションにつながってくれたらいいなと思っています。

完成形

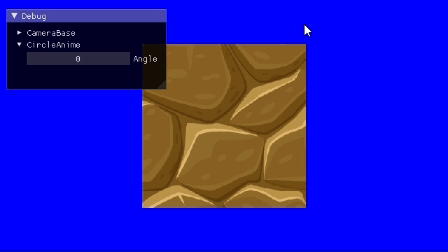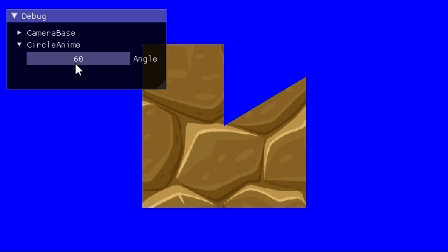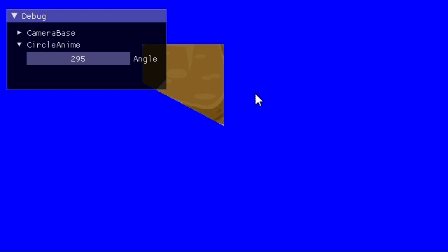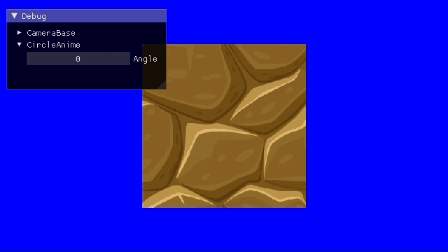
完成形.gif
スライダー（imgui）部分は作らないです。フリー素材拝借[1]

1.CPUから描画まで流れの確認

※2Dの画像描画が実装されている前提で話を進めます。

ex)敵のHPゲージとして実装
敵のHPがどれくらい減っているかを計算（角度換算）する
↓
CPU側の定数バッファ（角度情報）を設定
↓
CPUからGPUに定数バッファ（角度情報）を転送
↓
ピクセルシェーダで描画するorしないを決める

今回の記事では
ピクセルシェーダで描画するorしないを決める
の部分だけやります。

2.計算の考え方

完成形を想像してみる
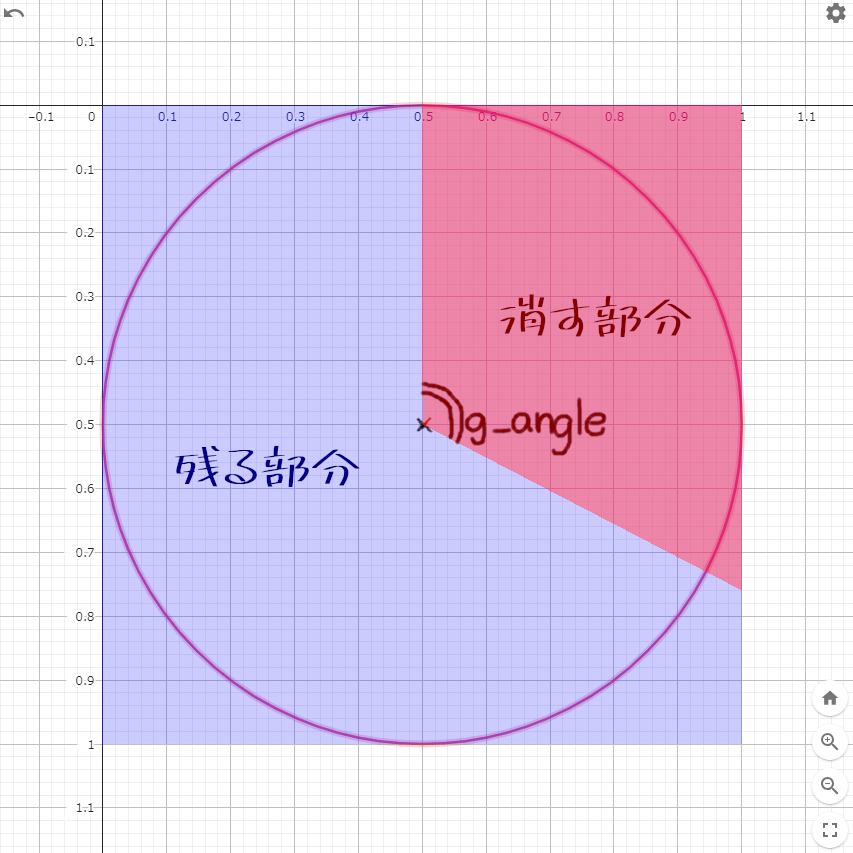
完成形.png
グラフのメモリはUV値を示す　g_angle...定数バッファ内の角度情報
赤色...描画しない　青色...描画する

赤色と青色の 条件部分 を解説していきます。

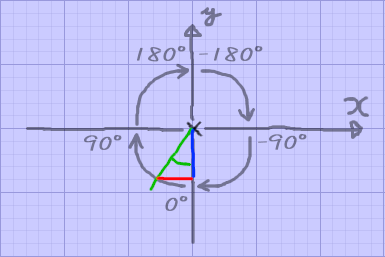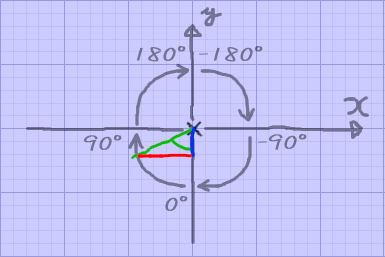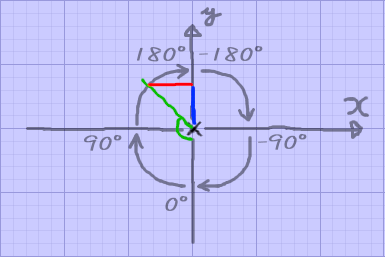
定義確認

atan2を使った場合の角度の数え方
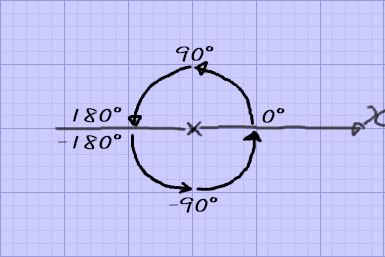
atan2の角度.png
atan2の戻り値はラジアン値であり、-3.14～3.14の範囲で返ってくる

またここではスタートとゴールの地点を基準軸と言うことにする
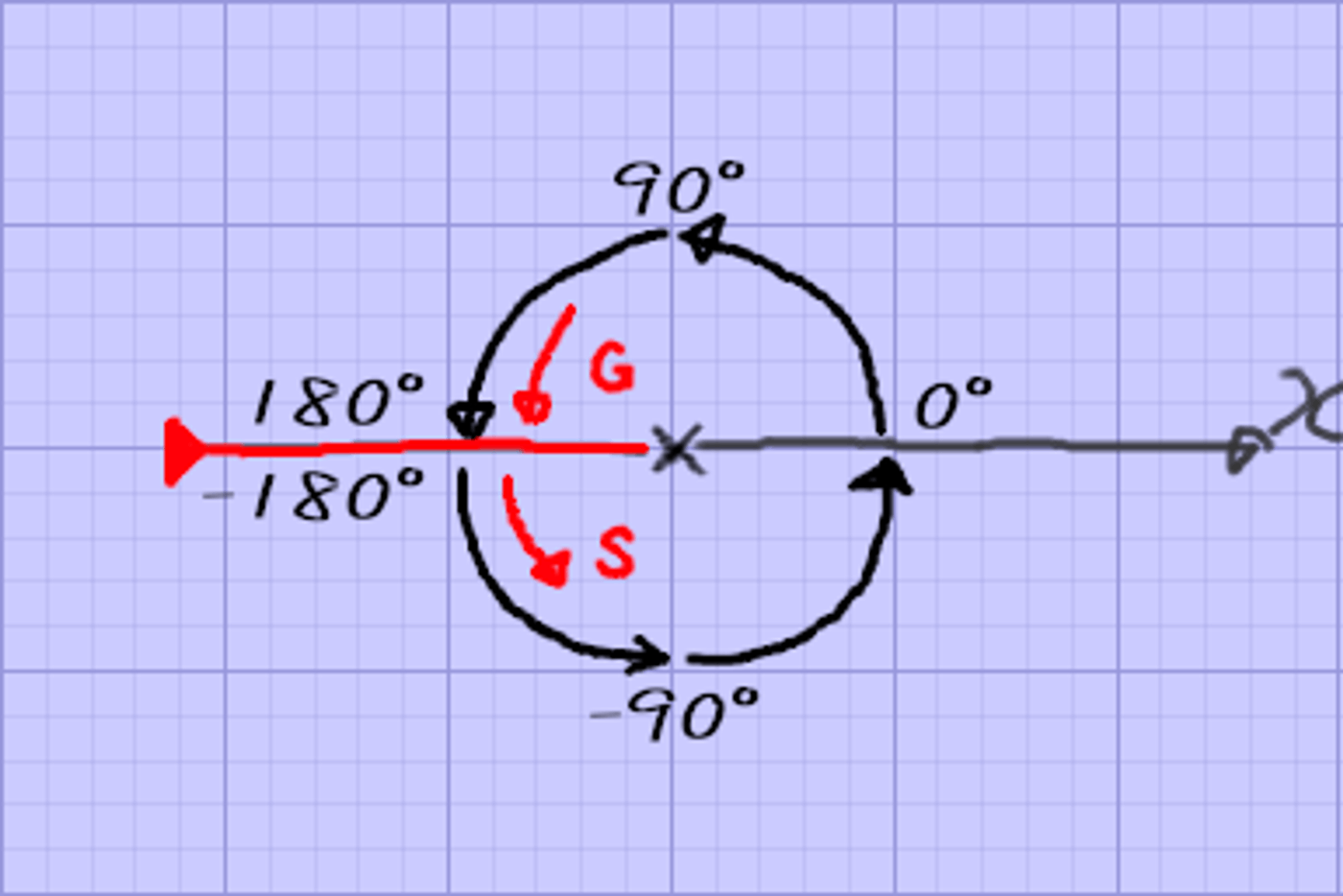
基準軸.png
X軸上の赤色の部分が基準軸
"基準軸"という言い方はこの記事内のみ
0°のところが基準と思いがちだが、一番小さい値と一番大きな値のところが基準軸となる。

基準軸を変えるには？回転方向を変えるには？
→ atan2で扱う部分を変える

プログラムで使うatan2は
三角比を利用して角度がわかる
というもの。

ただ数学が苦手な子ほど
xとyの距離で角度が出るもの　としか認識していない子が多い
今回の記事はそれで充分です。

三角関数、sincostan、がわからない人は
記事を見た後で他者様の解説記事[2]や動画[3]を見てください。

通常のtan
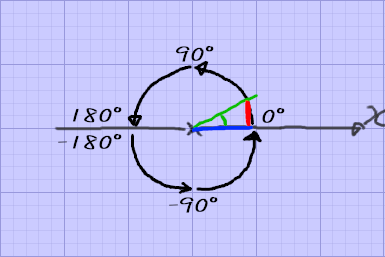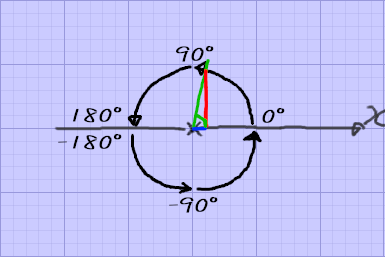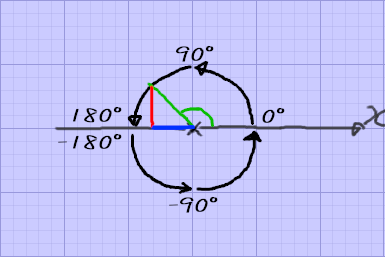
通常tan.gif
tan（角度）= 赤色(y値) / 青色(x値)

理想の基準軸と回転方向へ

理想の基準軸と回転方向を考えてみる
理想基準軸と回転方向.png

先ほど同様に角度がどう変化していくのか分かりやすくするため、
緑、赤、青の線を引いてみる
理想のtan.gif
理想のatan（角度）= 赤色(-x) / 青色(-y)

この考え方が理解できれば、基準軸や回転方向を自分好みにできますね。

最後に、
atan2の戻り値は-3.14～3.14の範囲で返ってくる。
正の値に統一しておくことで条件分岐がしやすい。
→ 最小値が0になるよう全体に数字を加える

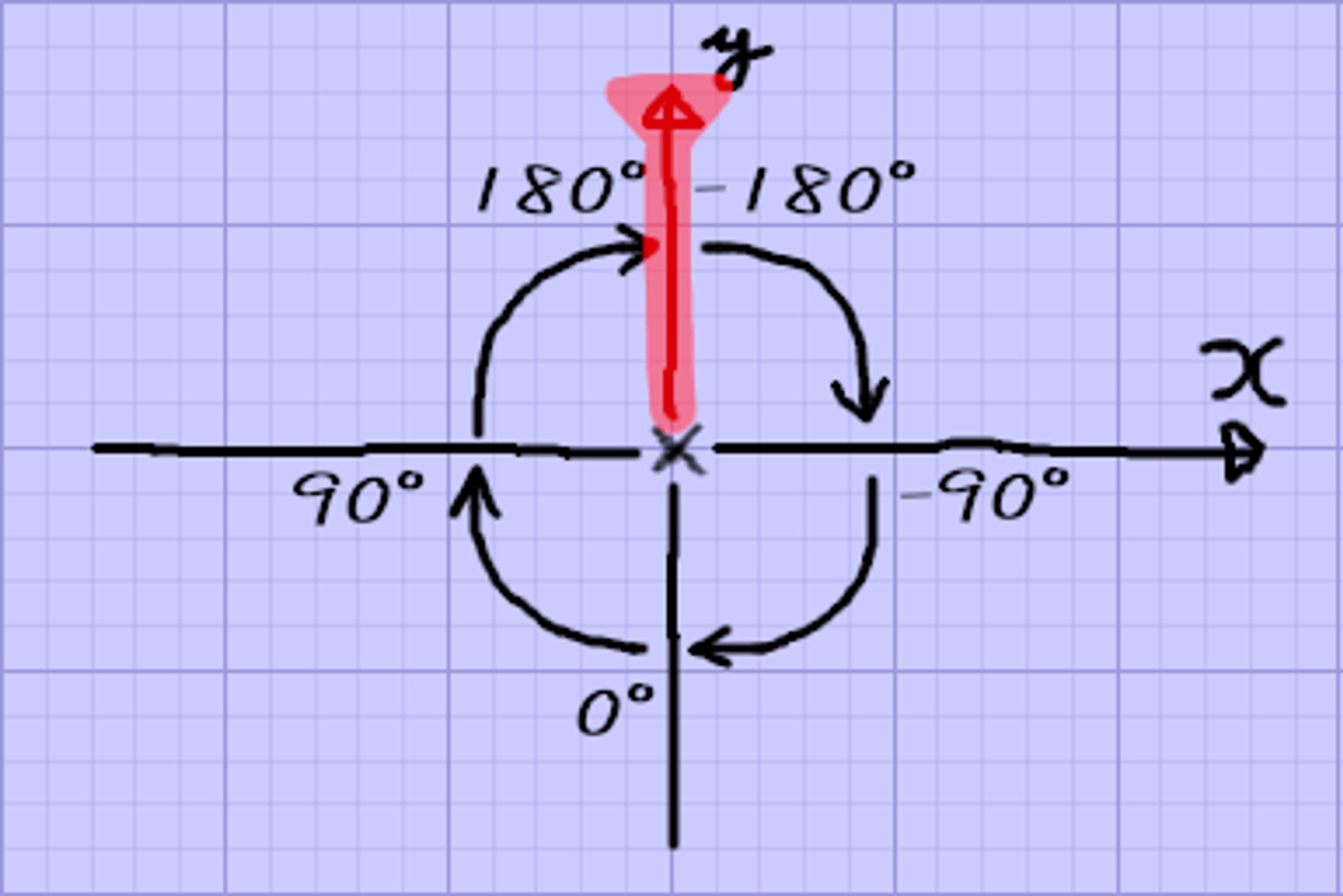
UVの値を調整する

数学では真ん中が(0,0)で考える。
UV座標は真ん中が(0.5,0.5)である
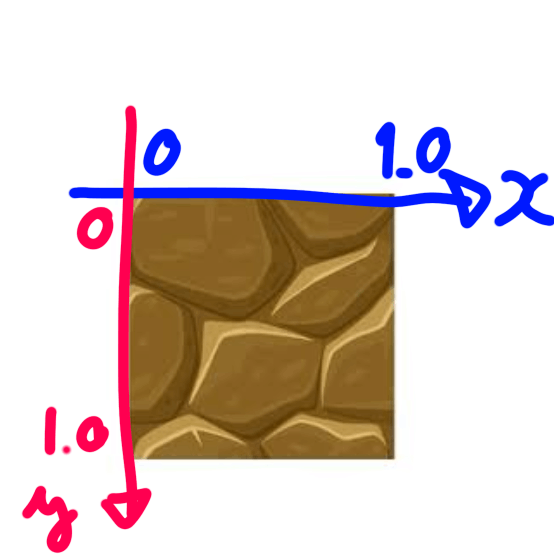
UV座標.png
図でみるUV座標　左上が(0,0) 右下が(1,1)

三角関数を使うとき中心が(0,0)であるので、
真ん中が(0,0)になるようにUVの値を変更する

先に理想を想像しておく

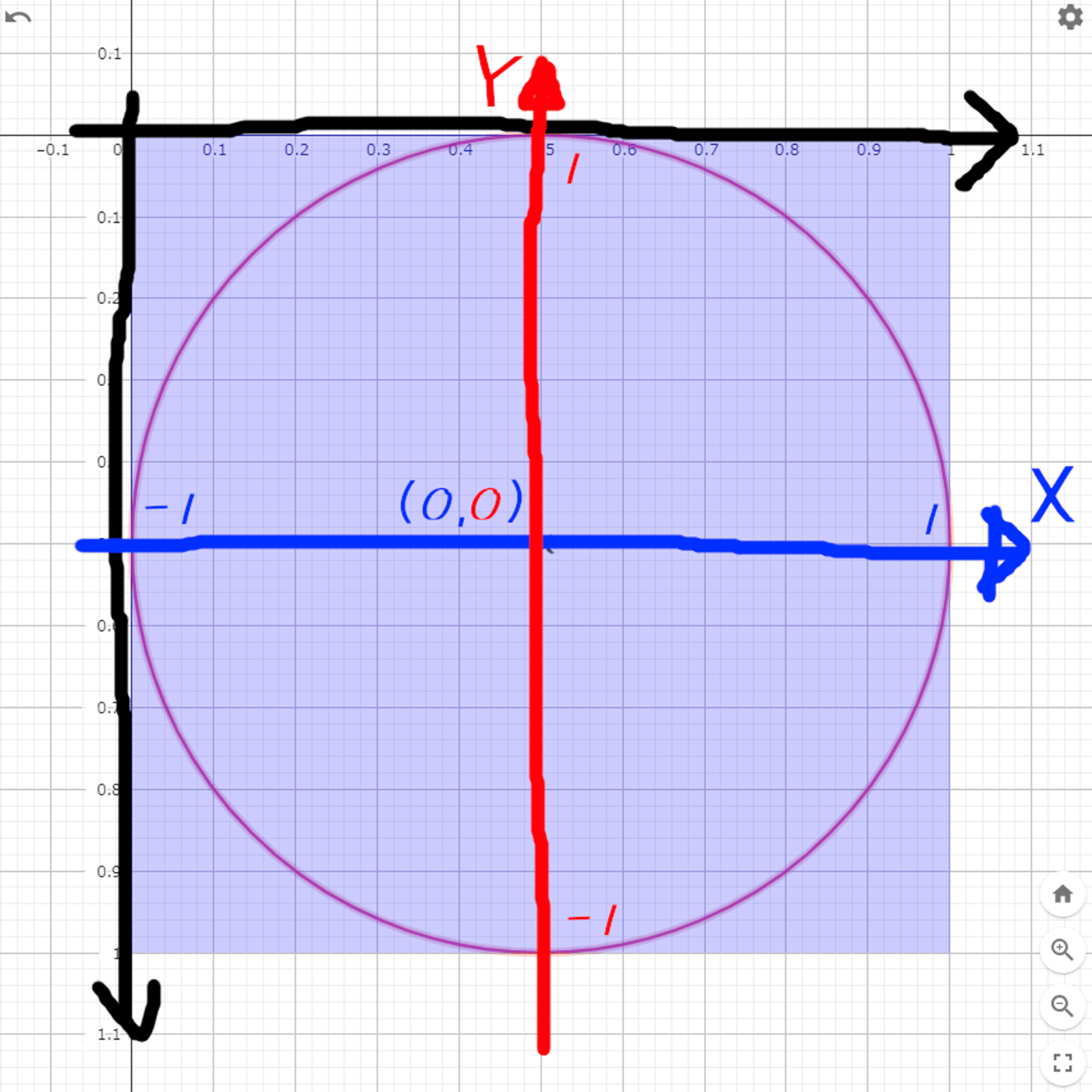
どう動かせば理想の軸になるのか

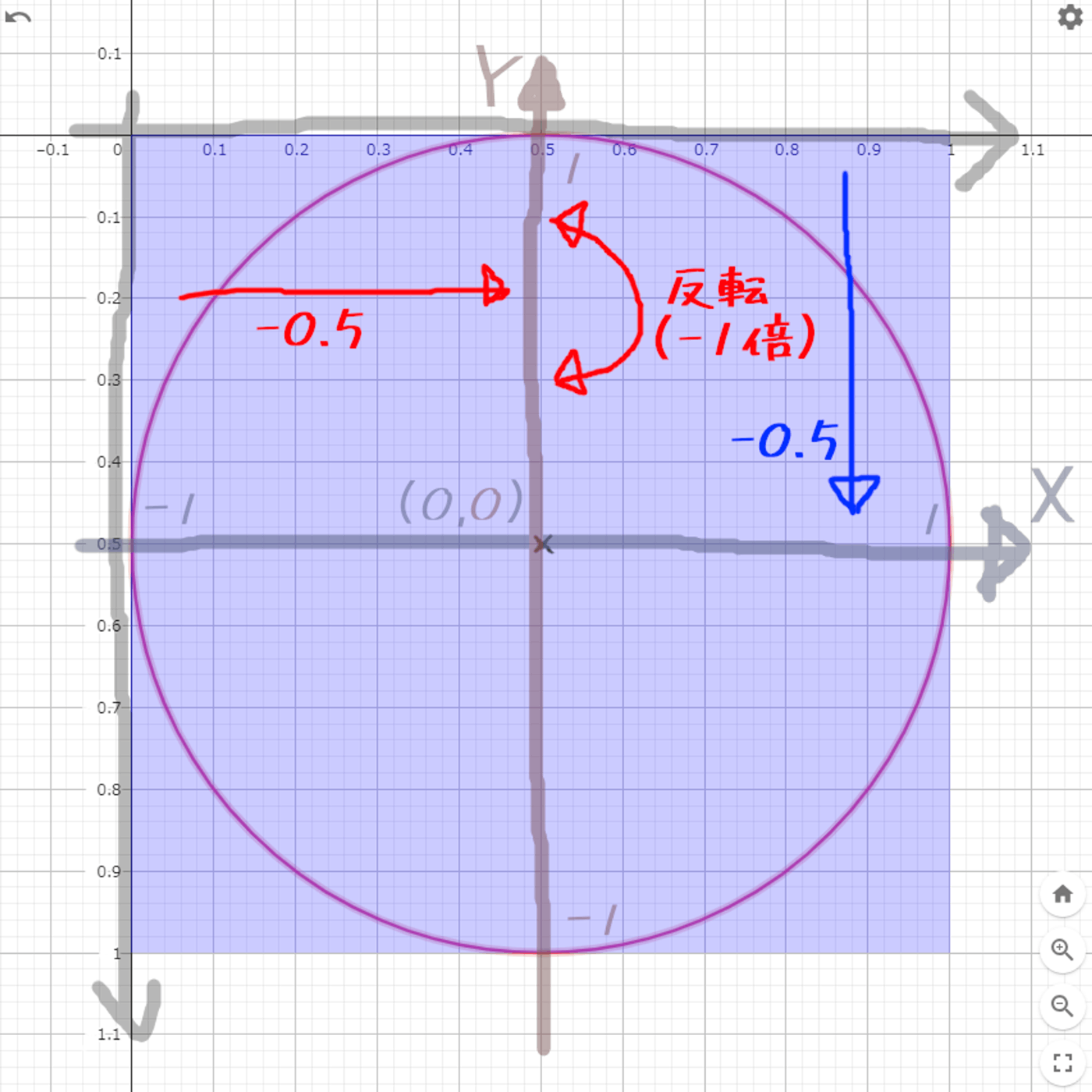
新しいUV.x = UV.x - 0.5
新しいUV.y = (UV.y - 0.5) * -1

3.変数などの定義確認

In … 頂点シェーダーからピクセルシェーダに送られてくる構造体変数
In.UV … テクスチャのどの位置のピクセルを示しているか。float型2つを持っていて、範囲はそれぞれ0～1.0　UV座標とは
g_○○ … 定数バッファの変数
g_angle … 角度情報(ラジアン)。ex)HPが減っている割合を角度換算する

角度換算方法

やり方：減っている部分の割合を求めて、角度換算する！！

減っている部分の割合とは…？
HPバーで考えるとわかりやすい。
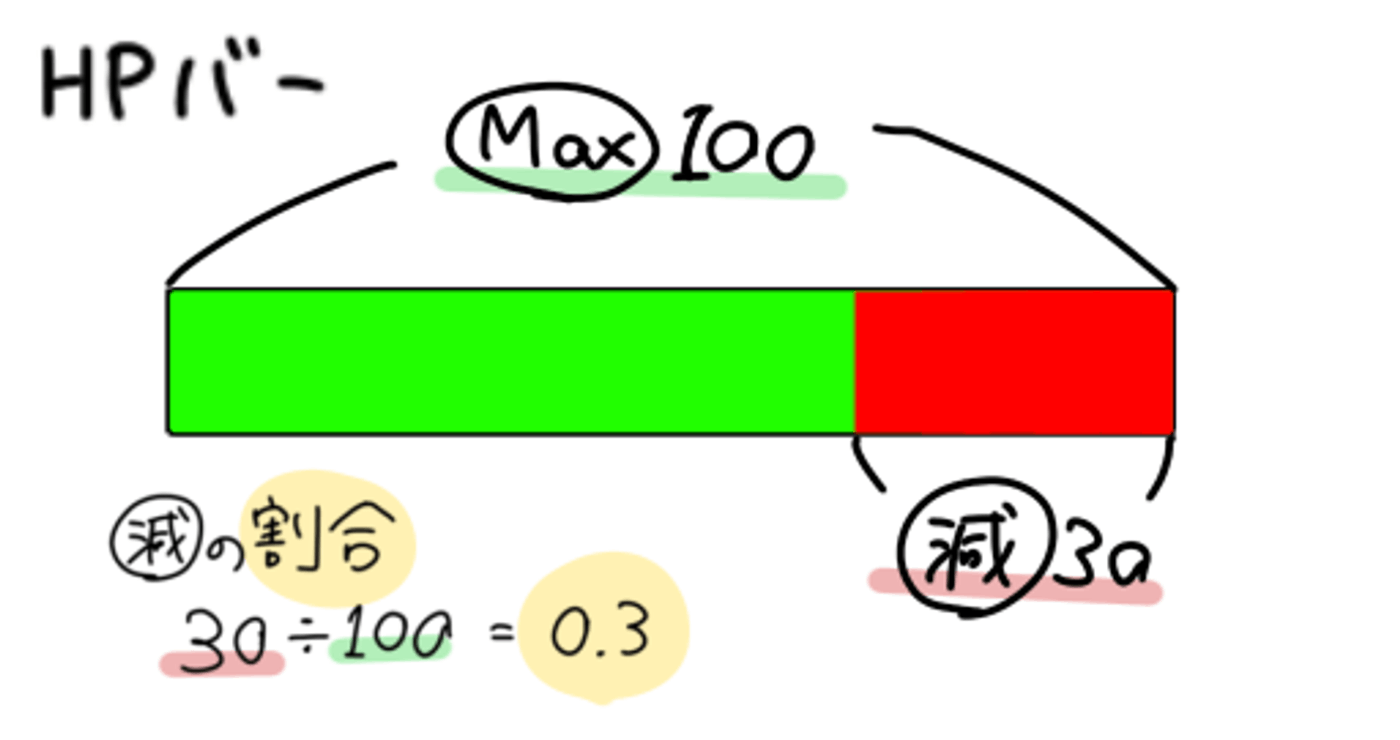
HPバーでの割合換算.png
求めたい部分 / 最大値 = 求めたい部分の割合

削られた部分を円形で考えてみる
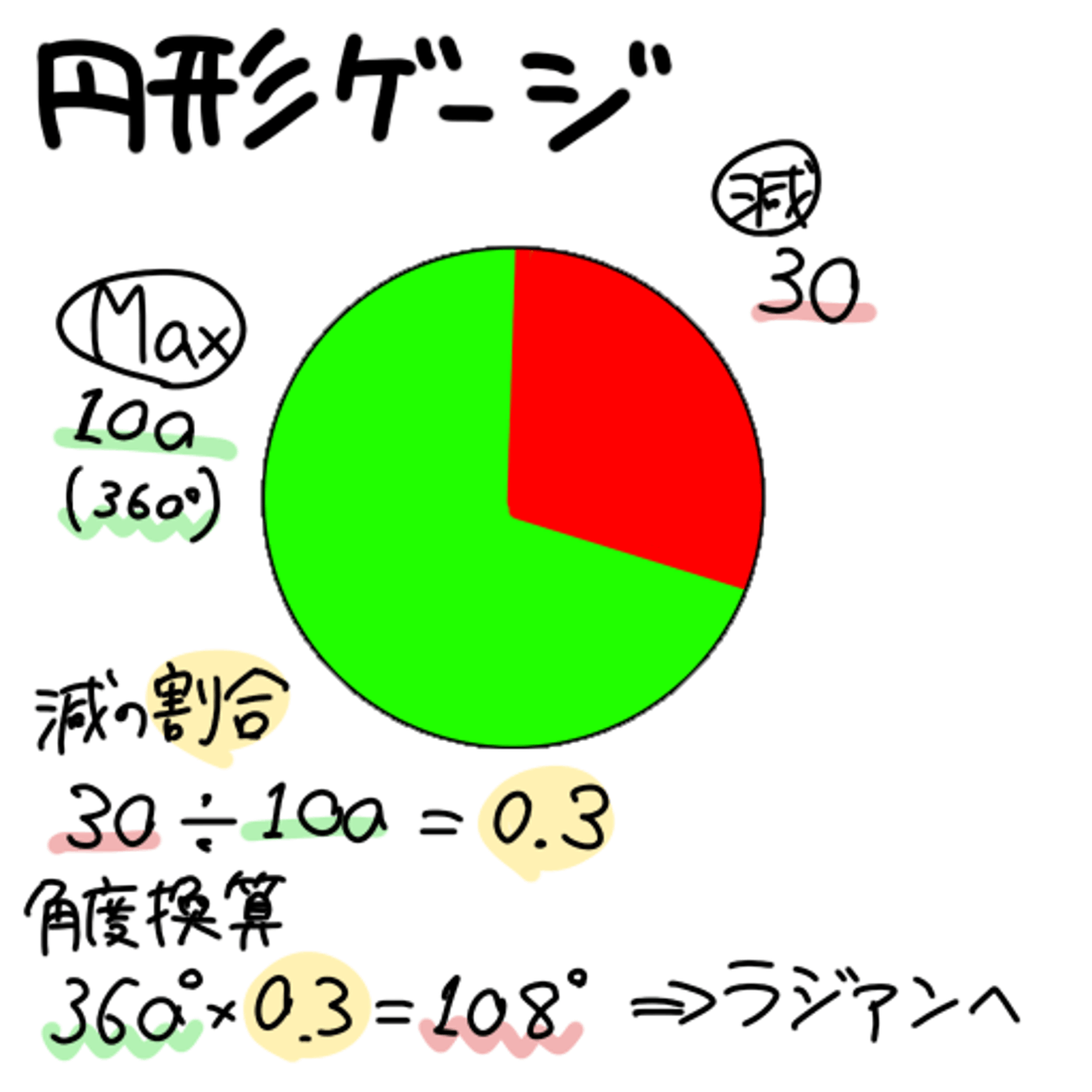
円形HPでの割合計算.png
割合が1.0の時（HPがすべて削られたとき）360度になる
逆に割合が0の時（HPが削られていないとき）0度

最大の角度 × 減った割合 = 減った部分の角度

4.シェーダープログラムで書く

ピクセルシェーダで描画するorしないを決めていくよ
HLSLで書いています。

SpriteShader_PS.hlsl
//============================================
// 2D描画 ピクセルシェーダ
//============================================
float4 main(VSOutput In) : SV_Target0
{    
    if (g_angle > 0.f)//値が入っている場合のみ処理する
    {
	//--------------------------------------------
	//描画しない条件に当てはまるか
	//--------------------------------------------
	
	//1.UVの値を考えやすくする
	//画像の中心が(0.5,0.5)だと難しいので
	//中心(0,0)にするために0.5を引く
        float uvX = (In.UV.x - 0.5f);
        float uvY = (In.UV.y - 0.5f) * -1.f; //上に行くほど数字が大きくなるようにするために-1をかける
 
        //2.距離からこのピクセルの角度をだす
        //基準となる軸からの距離を求める → atan2で角度を求める
        //-180になる位置が基準になる
        float blue = -1 * uvY;
        float red = -1 * uvX;
        float thisAngle = atan2(red, blue);
        	
        //3.値を修正
        //すべて正になるように180°加える
        thisAngle += 3.141592f;
        
        //4.定数バッファの角度と比較
        //定数バッファより小さかったら描画しない
        if (thisAngle < g_angle)
        {
            discard;//ここで終了　以下は読まれない
        }
    }
    
    /*アルファテストやテクスチャの色から値を返すetc..
	    割愛
    */
}

最後に.今後について

初めて記事書きました。
読んでいただいてありがとうございます。
図や記法に戸惑いつつ、見る人に伝わりやすい記事を目指しました。

改善点、疑問点ありましたらご連絡いただけると幸いです。
ご連絡はメッセージフォームかX（旧Twitter）のDMでよろしくお願いいたします。

またね！！

脚注

  1. 著作者：macrovector／出典：Freepik ↩︎

  2. https://www.optics-words.com/math/tri/trigonometric_ratio_3.html ↩︎

  3. ヨビノリ先生の授業大好きなのでぜひ https://youtu.be/OLqgs4fJl7Y?si=SB4onGNai-0Qk_a0 ↩︎

Discussion