📐

数式もコピペして使いたい〜Zennで使えるKaTeX版

2024/08/11に公開

 ♳ はじめに
 📋 数式ソースコードはコピペできるから良いぞっ卒論を書いたのが、もう10年以上も前ですが、またこうしてLaTeXで数式を書くことになるとは思わなんだ。
ZennではKaTexがサポートされているので[1]、いきって綺麗な数式を書くことが可能です。
そして、それがコピペで使い回せるのがとても素敵で、作業効率化できます。最の高。

 😭 ネットで見つけた数式が全部使えるわけではないネットで探してみるとそれっぽい数式コードが見つかりますが、それをZenn記事にコピペしても表示されない場合があります。
実は数式の書き方に微妙に違いがあったりなかったりして、KaTeXでサポートされている形式でしか表示されません。
多くの場合、パッケージ[2]や独自のマクロ定義[3]が使われていると思われます。知らんけど。

その場合は、頑張って修正するか、諦めるかしてください。

 ♴ 数式メモ
 🔔 事前分布に正規分布を過程するときに使う数式前書いたやつ。合ってるかは知らん。

 \pm \infinらへんだと0になる\lim_{x \to \pm \infin} {p(x)}	\simeq 0$$\lim_{x \to \pm \infin} {p(x)}	\simeq 0$$

 \pm 2\sigmaの間になる確率は大体95%\int^{2\sigma}_{-2\sigma} p(x) dx \simeq 0.95$$\int^{2\sigma}_{-2\sigma} p(x) dx \simeq 0.95$$

 全ての定義域で正の値 (インライン表記)p(x) > 0　(-\infty<x<\infty)
$p(x) > 0$　$(-\infty<x<\infty)$

 👀 "Attention is all you need."で出てくる数式みんな大好きTransformerの原論文[4]で出てくる数式も、texファイルをダウンロードして、数式をコピペできます。

画像にしてXにポストして存分にイキり散らかしてください。

 Attention機構\mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V$$\mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V$$
画像はこちら👇
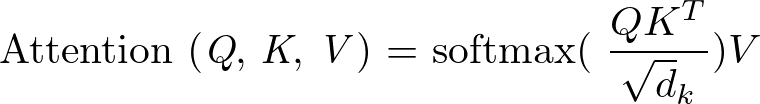
※（参考）イキった使い方
LINEで友達に画像を送信
「これ何か分かる？」
返信を待つ
「TransformerのAttention機構。原論文の"Attention is all you need."ってタイトルもいいけど、この数式も素敵だよね。」
ミュートされる。

 Justfication of the Scaling Factor in Dot-product Attentionデータをダウンロードして、texファイルを漁っていたら、「sqrt_d_trick.tex」ってファイルを発見しました。

発表論文には記載のないセクションで、冗長になるから削除したのかなぁと思われます。

詳細は、Scaled Dot-Product Attention[5]で調べると良いかもです。
詳細は省きますが、\sqrt{d_k}で割ってる理由について説明しているセクションです。
・・・

\begin{align*}
    E[<\vec{u},\vec{v}>] & =  \sum_k E[u_i v_i]\\
    & =\sum_k E[u_i]E[v_i]\\
    & = 0
\end{align*}
$$
\begin{align*}
    E[<\vec{u},\vec{v}>] & =  \sum_k E[u_i v_i]\\
    & =\sum_k E[u_i]E[v_i]\\
    & = 0
\end{align*}
$$

\begin{align*}
    E[(<\vec{u},\vec{v}>-E[<\vec{u},\vec{v}>])^2]  & = E[(<\vec{u},\vec{v}>)^2] - E[<\vec{u},\vec{v}>]^2 \\
    & = E[(<\vec{u},\vec{v}>)^2] \\
    & =  \sum_k E[{u_i}^2] E[{v_i}^2]\\
    & = d_k
\end{align*}
$$
\begin{align*}
    E[(<\vec{u},\vec{v}>-E[<\vec{u},\vec{v}>])^2]  & = E[(<\vec{u},\vec{v}>)^2] - E[<\vec{u},\vec{v}>]^2 \\
    & = E[(<\vec{u},\vec{v}>)^2] \\
    & =  \sum_k E[{u_i}^2] E[{v_i}^2]\\
    & = d_k
\end{align*}
$$

 ストロガッツ本に出てくる数式
 ローレンツ方程式
\begin{align*}
  \dot{x} &= \sigma (y-x) \\
  \dot{y} &= rx - y -xz \\
  \dot{z} &= xy -bz \\
\end{align*}
$$
\begin{align*}
  \dot{x} &= \sigma (y-x) \\
  \dot{y} &= rx - y -xz \\
  \dot{z} &= xy -bz \\
\end{align*}
$$

 Kuramoto model\dot{\varphi_s} = \omega_s + \dfrac{K}{N} \sum_r \sin{(\varphi_r - \varphi_s)} $$
\dot{\varphi_s} = \omega_s + \dfrac{K}{N} \sum_r \sin{(\varphi_r - \varphi_s)}
$$

 ♵ さいごに自分の数式ソースコード管理用に書いてみたので、また気が向いたら更新します。
実はわたしは、学術参考書や論文で数式がたくさん出てくるとあわあわなっちゃって読み飛ばしたくなる勢なのですが...
そんなだめなクセを治すために、手書きしたり、ソースコードに写経したりするみたいなことをしていました。
たくさん触れ合っていると、愛着が持てて、勉学が捗ると思うので、 まずはコピペから! 一歩踏み出してみてください♪

 ≡ 追記:勉強や研究をするのに、論文や学術参考書をまるっと読むのはなかなか大変で骨が折れますが、数式だけ見る のだと、まだ耐えられそう...でしょうか？
勉強の足がかりにも有名な数式（いっぱいあるなぁ...）[6]を写経して、簡単な紹介付きで記事にしていこうかなぁと思う今日この頃でした。

 ♶ 参考リンク
 🏠 KaTeX本家\KaTeX
[$\KaTeX$](https://katex.org/)
https://katex.org/docs/supported
大体ここで検索できます。
https://katex.org/#demo
オンライン上で試し打ちできます。

 🙏 数式を拝借できるサイトhttps://mathlandscape.com/category/latex/
分野ごとに記事にまとまっているので、探しやすく、周辺情報も学べて、とても勉強になります！
https://gitmind.com/faq/formula-list.html
英語だけど、みんな読めるよねっ!!

 🛐 数式の画像を出力できるサイトhttps://texclip.marutank.net/
数式コードを画像変換できるオンラインツール。

出力形式が、PNG、EPS、SVGなのが神。

脚注
ZennのMarkdown記法一覧 https://zenn.dev/zenn/articles/markdown-guide#数式 ↩︎
physics2 – Macros for typesetting maths faster and more simply | CTAN

Comprehensive TeX Archive Network https://www.ctan.org/pkg/physics2 ↩︎
Defining TeX macros | MathJax https://docs.mathjax.org/en/latest/input/tex/macros.html ↩︎
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30. https://arxiv.org/abs/1706.03762 ↩︎
Scaled Dot-Product Attention Explained | Papers With Code https://paperswithcode.com/method/scaled ↩︎
List of equations | Wikipedia https://en.wikipedia.org/wiki/List_of_equations ↩︎

数式もコピペして使いたい〜Zennで使えるKaTeX版

♳ はじめに

📋 数式ソースコードはコピペできるから良いぞっ

😭 ネットで見つけた数式が全部使えるわけではない

♴ 数式メモ

🔔 事前分布に正規分布を過程するときに使う数式

$\pm \infin$ らへんだと0になる

$\pm 2\sigma$ の間になる確率は大体95%

全ての定義域で正の値 (インライン表記)

👀 "Attention is all you need."で出てくる数式

Attention機構

Justfication of the Scaling Factor in Dot-product Attention

ストロガッツ本に出てくる数式

ローレンツ方程式

Kuramoto model

♵ さいごに

≡ 追記:

♶ 参考リンク

🏠 KaTeX本家

🙏 数式を拝借できるサイト

🛐 数式の画像を出力できるサイト

Discussion