入門: Long Short-Term Memory(LSTM)ネットワーク
こんにちは、AI実践喫茶店です。
今回は、Pytorchで簡単なLSTMモデルを作って、そのモデルを利用出来るようになりましょう。
今回作成したモデルはこちら(Github)で配布しています。
ぜひ自分の調整をしてください。
はじめに
時系列データのモデリングや予測において、リカレントニューラルネットワーク(RNN)は有力なツールとなっています。その中でも、LSTM(Long Short-Term Memory)は短期的および長期的な依存関係を学習する能力に優れ、広く使用されています。この記事では、LSTMの基本原理、PyTorchを用いた実装手順、そして実際のデータにLSTMを適用する方法に焦点を当てます。
LSTMの基本原理
LSTMは、通常のRNNが直面する勾配消失問題を解決するために開発されました。このネットワークは、ゲート(input gate、forget gate、output gate)を導入することで、長期的な記憶の保持と選択的な情報の取捨選択を可能にします。これにより、LSTMは長期的な依存関係を学習しやすくなります。
PyTorchでのLSTMの実装
PyTorchを使用したLSTMの実装は直感的であり、以下は基本的な手順です。
class LSTMPredictor(nn.Module):
def __init__(self, input_size=1, hidden_size=8, num_layers=2, output_size=1, dropout_prob=0.2):
super(LSTMPredictor, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.dropout = nn.Dropout(dropout_prob)
# create lstm cells list
self.lstm_cells = nn.ModuleList([nn.LSTMCell(input_size, self.hidden_size)])
# add the lstm cells
for _ in range(num_layers - 1):
self.lstm_cells.append(nn.LSTMCell(hidden_size, hidden_size))
# linear layer for output
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x, future=0):
h_t = [torch.zeros(x.size(1), self.hidden_size, dtype=x.dtype, device=x.device)]
c_t = [torch.zeros(x.size(1), self.hidden_size, dtype=x.dtype, device=x.device)]
outputs = []
# loop through the LSTM cells
for i in range(self.num_layers-1):
h_t.append(torch.zeros(x.size(1), self.hidden_size, dtype=x.dtype, device=x.device))
c_t.append(torch.zeros(x.size(1), self.hidden_size, dtype=x.dtype, device=x.device))
for time_step in range(x.size(0)):
h_t[0], c_t[0] = self.lstm_cells[0](x[time_step], (h_t[0], c_t[0]))
for i in range(self.num_layers-1):
h_t[i+1], c_t[i+1] = self.lstm_cells[i+1](h_t[i], (h_t[i+1], c_t[i+1]))
output = self.dropout(h_t[-1])
output = self.linear(output)
outputs += [output]
for i in range(future):
h_t[0], c_t[0] = self.lstm_cells[0](output, (h_t[0], c_t[0]))
for i in range(self.num_layers-1):
h_t[i+1], c_t[i+1] = self.lstm_cells[i+1](h_t[i], (h_t[i+1], c_t[i+1]))
output = self.dropout(h_t[-1])
output = self.linear(output)
outputs += [output]
outputs = torch.cat(outputs, dim=1)
return outputs
最初はLSTMPredictorのクラスの初期化です。次のようなパラメータがあります。
- input_size: 入力データの特徴量の数(デフォルトは1)。
- hidden_size: LSTMセルの隠れ層の次元数。
- num_layers: LSTMセルの層数。
- output_size: モデルの出力の次元数。
- dropout_prob: ドロップアウトの確率。
その後、LSTMセルの構築を行います、nn.LSTMCell を使用してLSTMセルを構築し、それを複数の層分リストに格納します。隠れ状態 h_t とセル状態 c_t も構築されてます、LSTMセルと同じように。
最後に、順伝播関数 (forward メソッド)の出番です。
入力データ x が各LSTMセルを通過し、隠れ状態 h_t とセル状態 c_t が更新されます。
ドロップアウトが適用され、線形層で出力が生成されます。未来の予測も同様に行われ、出力が蓄積されます。
このLSTMモデルは、株価の時系列データを学習し、未来の予測を生成するのに利用されるものです。 input_size が1であるため、単変量時系列データ(たとえば日次の株価)に適しています。
時系列データの予測におけるLSTMの活用
LSTMは時系列データの予測に非常に有効です。例えば、株価の予測や天候の変動の予測など、さまざまな応用が考えられます。データをネットワークに供給し、訓練することで、LSTMは系列データのパターンを学習し、未来の値を予測することができます。
Dataset
このクラスは3つのメソッドがあります、一個づつ理解しましょう。
def preprocess(self, data):
data['Date'] = pd.to_datetime(data['Date'])
# order the values, even if they are already
data = data.sort_values(by='Date', ascending=True)
time_series = data['Close'].values
return time_series
def normalize(self, data):
min_value = data.min()
max_value = data.max()
normalized_array = 2 * (data - min_value) / (max_value - min_value) - 1
return normalized_array
この2つのメソッドは事前処理です。最初のメソッドは日付を日付の形に変える、もしstrフォーマットでいれば、変える必要がある。
2つ目は正規化する、この部分は時系列データを作ったあとで実行する。
そのあとは実際の時系列データを作ります。
def init_dataset(self, includeInput):
time_series = self.preprocess(self.df)
x = []
y = []
for i in range(len(time_series) - self.sequence_length - self.future_time_steps + 1):
# Input data (past values)
x.append(time_series[i : i + self.sequence_length])
# Target data (future values)
if includeInput == True:
y.append(time_series[i : i + self.sequence_length + self.future_time_steps])
else:
y.append(time_series[i + self.sequence_length : i + self.sequence_length + self.future_time_steps])
x = np.stack(x)
y = np.stack(y)
# Convert input and target data to PyTorch tensors
x = torch.from_numpy(x)
y = torch.from_numpy(y)
x = x.view(len(x), 1, -1) # Shape: (batch_size, input_size, sequence_length)
if includeInput == True:
# Shape: (batch_size, self.sequence_length + future_time_steps)
y = y.view(len(y), self.sequence_length + self.future_time_steps)
else:
# Shape: (batch_size, future_time_steps)
y = y.view(len(y), self.future_time_steps)
このメソッドは、株式市場の時系列データをPyTorchのフォーマットに変換し、モデルの学習に使用できるようにすることを目的としています。
入力データ(過去の値)とターゲットデータ(将来の値)を含む、適切なサイズのウィンドウが生成されます。self.sequence_lengthは、モデルが考慮する過去のデータの数を指定します。
self.future_time_stepsは、モデルが予測する未来のデータの数を指定します。
xは形状を (batch_size, input_size, sequence_length) に変更されます。yは、includeInputがTrueの場合は (batch_size, self.sequence_length + future_time_steps)、そうでない場合は (batch_size, future_time_steps) に変更されます。
LSTMの損失関数とトレーニング
LSTMモデルを訓練するためには、損失関数と最適化手法の選択が重要です。一般的な回帰タスクでは、平均二乗誤差(MSE)が使用されます。トレーニング中には、バックプロパゲーションと勾配降下法を使用してモデルを最適化します。
学習
学習は三つの関数が必要、一番重大はcomputeBatchLossだから最初はその関数を見ましょう。
def computeBatchLoss(self, batch_idx, batch_tuple, batch_size, batch_metrics):
x_batch, y_batch = batch_tuple
x_batch = x_batch.permute(2, 0, 1)
x_batch_gpu = x_batch.to(self.device)
y_batch_gpu = y_batch.to(self.device)
outputs = self.model(x_batch_gpu, self.args.future_time_steps)
loss_func = nn.MSELoss(reduction='none')
loss_gpu = loss_func(
outputs,
y_batch_gpu,
)
start_idx = batch_idx * batch_size
end_idx = start_idx + y_batch.size(0)
batch_metrics[METRICS_VALUE_NDX, start_idx:end_idx, :] = y_batch_gpu
if self.includeInput:
batch_metrics[METRICS_PRED_NDX, start_idx:end_idx, :] = outputs[:,:y_batch.shape[1]]
else:
batch_metrics[METRICS_PRED_NDX, start_idx:end_idx, :] = outputs
batch_metrics[METRICS_LOSS_NDX, start_idx:end_idx, :] = loss_gpu
return loss_gpu.mean()
引数について、batch_tupleは入力データとターゲットデータを含むバッチのタプル、batch_metricsは メトリクスの値を格納するテンソル。このメトリクスは学習関数で作られる、そこで価値と予測と損失が保存されてる。この場合はMSEを使います。
def TrainingEpoch(self, epoch, train_loader):
if self.includeInput == True:
batch_metrics_train = torch.zeros(METRICS_SIZE, len(train_loader.dataset), self.args.future_time_steps + self.args.sequence_length, device=self.device)
else:
batch_metrics_train = torch.zeros(METRICS_SIZE, len(train_loader.dataset), self.args.future_time_steps, device=self.device)
self.model.train()
for batch_idx, batch_tuple in enumerate(train_loader):
self.optimizer.zero_grad()
loss_var = self.computeBatchLoss(
batch_idx,
batch_tuple,
train_loader.batch_size,
batch_metrics_train,
)
loss_var.backward()
self.optimizer.step()
self.totalTrainingSamples_count += len(train_loader.dataset)
return batch_metrics_train.to('cpu')
最初は前紹介したメトリクスのテンソルを実装して、モデルを学習モードを設定して、DataLoaderからバッチを取得する。各バッチに対して以下の処理が行われます、勾配をゼロに設定し self.optimizer.zero_grad()。
computeBatchLossメソッドによってバッチの損失が計算され。その後、バックワード勾配伝播と最適化が行われます。最後にトレーニング中に計算されたバッチのメトリクスが返されます。
LSTMモデルの評価とメトリクス
訓練が終了したら、モデルの評価が行われます。予測と実際の値の比較には、RMSE(Root Mean Squared Error)、MAE(Mean Absolute Error)、R²(Coefficient of Determination)などのメトリクスが利用されます。そのメトリクスはこの関数によってもっと深い分析ができます。
def logMetrics(
self,
epoch,
phase,
metrics,
):
"""
Root Mean Squared Error (RMSE):
rmse = torch.sqrt(loss)
Mean Absolute Error (MAE):
mae = torch.mean(torch.abs(predictions - targets))
Percentage Explained
variance_targets = torch.var(targets)
percentage_explained = 1 - loss / variance_targets
Prediction Direction Accuracy (PDA):
correct_direction = ((predictions[1:] - predictions[:-1]) * (targets[1:] - targets[:-1])) > 0
pda = torch.mean(correct_direction.float())
Coefficient of Determination (R²)
variance_targets = torch.var(targets)
r_squared = 1 - (loss / variance_targets)
Explained Variance Score
explained_variance = 1 - (loss / variance_targets)
Normalized RMSE (NRMSE):
range_targets = torch.max(targets) - torch.min(targets)
nrmse = rmse / range_targets
"""
loss = metrics[METRICS_LOSS_NDX].mean()
rmse = torch.sqrt(loss)
mae = torch.mean(torch.abs(metrics[METRICS_PRED_NDX] - metrics[METRICS_VALUE_NDX]))
variance_targets = torch.var(metrics[METRICS_VALUE_NDX])
correct_direction = ((metrics[METRICS_PRED_NDX, 1:] - metrics[METRICS_PRED_NDX, :-1]) * (metrics[METRICS_VALUE_NDX, 1:] - metrics[METRICS_VALUE_NDX, :-1])) > 0
pda = torch.mean(correct_direction.float())
r_squared = 1 - (loss / variance_targets)
range_targets = torch.max(metrics[METRICS_VALUE_NDX]) - torch.min(metrics[METRICS_VALUE_NDX])
nrmse = rmse / range_targets
metrics_dict = {}
metrics_dict['loss'] = metrics[METRICS_LOSS_NDX].mean()
metrics_dict['RMSE'] = rmse
metrics_dict['MAE'] = mae
metrics_dict['PDA'] = pda
metrics_dict['r_squared'] = r_squared
metrics_dict['NRMSE'] = nrmse
time = datetime.datetime.now()
log.info(
("Time {} | Epoch {} | Phase {} | Loss: {:.4f} | RMSE: {:.4f} | MAE: {:.4f} |"
+ " PDA: {:.4f} | r_squared: {:.4f} |"
+ " NRMSE: {:.4f}").format(
time, epoch, phase,
metrics_dict['loss'].item(), metrics_dict['RMSE'].item(),
metrics_dict['MAE'].item(),
metrics_dict['PDA'].item(), metrics_dict['r_squared'].item(),
metrics_dict['NRMSE'].item()
)
)
writer = getattr(self, 'writer_' + phase)
for key, value in metrics_dict.items():
writer.add_scalar(key, value, self.totalTrainingSamples_count)
このメソッドは、トレーニングまたは検証の各エポック後にログにメトリクスを記録するためのものです。以下は、このメソッドの主な機能と手順の概要です。コードでメトリクスの名前や計算方法が指摘されてる。
その後各メトリクスの平均値が取得され、ログメッセージが構築されます、ターミナルで読めるから学習してる時にとても便利だと思います。最後にTensorBoardにメトリクスの値が書き込まれます。各メトリクス(loss、RMSE、MAEなど)に対して、エポックごとに値が書き込まれます。
推論の実行
トレーニングされたモデルを使用して、未来の株価動向を予測しました。予測の精度は、テストデータを使用して評価されました。我々はモデルの性能を評価するために、異なる評価指標を使用しました。
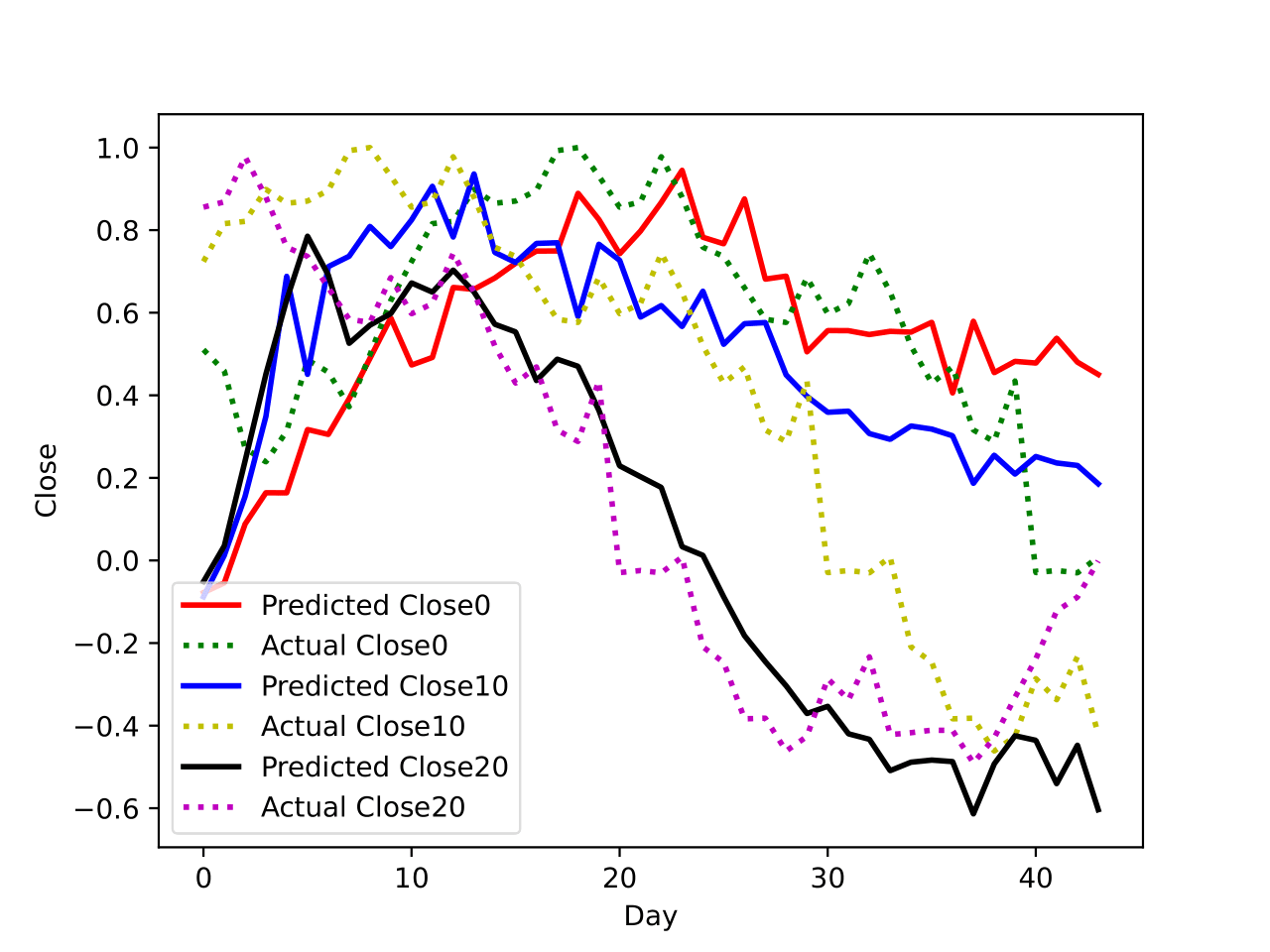
生憎、モデルは株式市場の価格予測が正確に出来ない、でもLSTMの仕組みや強さが分かるようになりました。他のモデルや特徴量エンジニアリングを行うなら、きっと精度を上がることが出来ます。
おわりに
このPyTorchを使用したLSTMモデルは、株価の予測に活用されるもので、単変量時系列データに対応しています。異なるデータや予測の要件に調整可能なパラメータを備え、効率的な学習と予測が可能です。提供されたコードは、LSTMモデルの基本的な理解と活用を支援します。これは時系列データの予測への一歩であり、興味深いプロジェクトや研究に活かせるでしょう。ぜひ手を動かしてみてください。お疲れさまでした。
コード
コードは全部GitHubに登録された。
Discussion