LoRA: Low-Rank Adaptaion of Large Language Models の解説

こんにちは、初めましての方は初めまして。株式会社 Fusic の瓦です。夏用と冬用の服しか持っていない自分にとって、暖かいのか寒いのか分からないこの季節は過ごし方が分からなくなりがちです。

この記事では LoRA: Low-Rank Adaptaion of Large Language Models (以降 LoRA として参照) の解説をします。学習済みモデルや実装は Github のページ に載っています。

概要

一言で言えば、LoRA は効率的な追加学習手法の一つです。単純なファインチューニングでは、訓練時にモデルのパラメータを全て保持しつつパラメータの更新を行わなければならないため、ベースにするモデルによっては莫大なメモリが必要となります。また、追加で学習させたいタスクそれぞれに対してモデルが必要となります。大きなモデルを使用するとモデル一つに対してサーバが複数必要となることがあり、かつ複数のモデルを用意するとその分必要なサーバーが多くなるため、莫大なコストがかかってしまいます。

Fig.1 より引用

この問題に対して、論文では元のパラメータを更新せずに、差分を計算するモデルを学習するアプローチを提案しています。上図のように、元のパラメータに対して、行列分解するモデルを学習させています。この手法によって、GPT-3 を単純に追加学習する場合と比較して学習に必要なパラメータ数は 1/10000 になり、使用する GPU のメモリは 1/3 になったとのことです。また、他の先行研究と比較して学習に必要なパラメータが少ないにもかかわらず、多くのタスクにおいて同等の結果、またはより良い結果を出しています。

提案手法

ファインチューニングは、元のパラメータを $W$ とするとファインチューニング後のパラメータ $W'$ を

$$W' = W + \Delta W$$

となるように学習しているとみなすことが出来ます。ここで $\Delta W$ は元のパラメータとファインチューニング後のパラメータの差分を表します。

提案手法ではこの差分を効率的に学習する方法を提案しています。元のパラメータが $W \in \mathrm{R}^{d×k}$ であるとすると、$B\in \mathrm{R}^{d×r}$ と $A\in \mathrm{R}^{r×k}$ を使用して $\Delta W = BA$ となるように $B$ と $A$ の学習を行います。

ここでパラメータ数の違いに注目してみましょう。簡単に $W \in \mathrm{R}^{d×d}$ とします。単純なファインチューニングでは $\Delta W$ を学習するので、学習するパラメータ数は $d^2$ です。一方で提案手法では $A$, $B$ をそれぞれ学習するので、学習するパラメータ数は $2dr$ となります。$r \ll d$ の場合、提案手法によって学習するパラメータ数は元のパラメータ数より少なくなります。

ここで一つ疑問になることがあります。入力を $x$ としたとき、ファインチューニングのモデルの出力 $h$ は

$$h = W'x = (W + \Delta W)x = (W + BA)x$$

と表されます。$BA$ の部分では、概要で引用した図のようにいったん低次元のベクトルに落とした後に復元する、という動作をしています。元々巨大なパラメータで学習したものを低次元に落としてもうまくいくのでしょうか、うまくいくならそれは何故なのでしょうか？

このことについては論文内で Aghajanyan et al., 2020 を参考にしたと書いてあります。詳細が気になる方は元の論文を読んでほしいのですが、簡単に言うと、ファインチューニングで必要となるベクトルの次元は元のモデルの次元と比較して少なく済むという主張の論文です（僕の解釈が間違っていたらすみません）これに着想を得たのが提案手法となります。

先行研究との比較

追加のデータで効率的に学習を行う先行研究として、

1. 追加のモデルを計算途中に直列で挿し込む方法
2. プロンプトを工夫する方法
   の 2 つが挙げられています。

追加のモデルを直列で挿し込む方法では、元のモデルと比べて入力から出力までにかかる時間が増えてしまうことが問題として挙げられています。また、プロンプトを工夫する方法では、プロンプトをどのように最適化すべきかが難しいという点が問題としてあります。また、入力の一部を使用するために自由に入力できるテキストの長さが短くなってしまうということも問題として挙げられています。これらに対して、提案手法では入力から出力までにかかる時間は変わらず、また入力の一部を使用しないので入力できるテキストの長さは変わらないというメリットがあります。

実験結果

ファインチューニングの対象にするパラメータとして、Transformer のパラメータである $W_q, W_k, W_v, W_o$ を対象としています。実験で使用したモデルは RoBERTa, DeBERTa, GPT-2, GPT-3 です。ここでは、RoBERTa, DeBERTa の結果について見てみます。

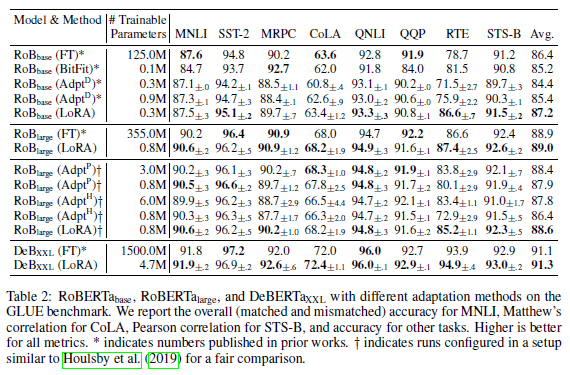
RoBERTa と DeBERTa による各タスクでの実験 (Tab. 2 より引用)

RoBERTa や DeBERTa での実験では、多くのタスクにおいて提案手法である LoRA が既存手法やファインチューニング (図内で FT の行) の同等のスコア、または最高のスコアを達成しています。特に訓練するパラメータを見てみると、ファインチューニングのパラメータ数と比較して圧倒的に少ないパラメータで済んでいることがわかります。

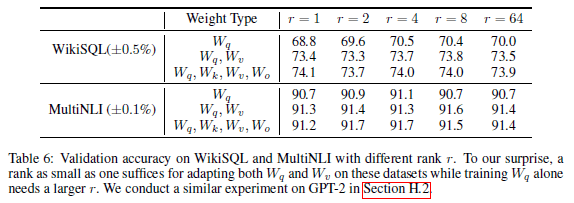
次に、適用するパラメータと $r$ の変化によってどのように結果が変わるかを見てみます。

$r$ と学習するパラメータによるスコアの変化 (Tab. 6 より引用)

$r$ をかなり小さくしてもいいスコアを達成できていることが分かります。特に、$r=1$ でもほとんどスコアが落ちていないことには驚嘆します。また、$r$ を大きくすれば大きくするほど良くなる訳ではないという部分も面白い結果だと思います。タスクによって最適な $r$ があるのかなどは気になる点です。

まとめ

この論文では LoRA について解説しました。入力と元のモデルの出力があれば、それをもとにしてとても軽いモデルで学習が行えるので、自分が用意したデータでパパっとファインチューニングなんかも簡単に出来そうです。今回は言語モデルに対してのアプローチでしたが、この次元を落として必要なパラメータ数を少なくする方法はかなり汎用的に使えるんじゃないかと思っています。余裕があれば、実装を動かして挙動を確認してみようと思います。

最後に宣伝になりますが、機械学習でビジネスの成長を加速するために、Fusicの機械学習チームがお手伝いたします。機械学習のPoCから運用まで、すべての場面でサポートした実績があります。もし、困っている方がいましたら、ぜひFusicにご相談ください。お問い合わせからでも気軽にご連絡いただけます。またTwitterのDMからでも大歓迎です！