0から作るLLMーLlama

本記事の対象読者：

• LLM（大規模言語モデル）の複雑な構造や階層を理解しているが、それをどのように組み合わせるかが分からない人
• LlaMaモデルに関するすべてのオペレータとアーキテクチャ（RMSNorm、ROPE、SwiGLUの実装を含む）を一行ずつ分解します。
• 本記事ではhuggingfaceのライブラリを使用しておらず、すべてpytorchで実装しています。また、事前学習済みモデルも使用していません。
• スタート地点は『源氏物語』の原文であり、ゴール地点はあなた自身がトレーニングした大規模モデルです。
• pytorchを準備してください。GPUがなくても大丈夫です。重要なのはLLMの原理を学ぶことであり、この文章を読んだだけで新しい大規模モデルのアーキテクチャを作れるわけではありません。
• 本記事では、できる限り平易な言葉を使って原理を解説していきます。

序文

本記事のすべてのコードはGoogle Colabに共有されています。コードには一行ずつコメントが付いていますので、記事を読むのが面倒な方は、直接Colab上で実行してみてください。GPUリソースは必要なく、最小構成のCPUで実行できます。

https://colab.research.google.com/drive/1OWuSYxcMtkMwc5JygEFz5FRR_VpM_EAw?usp=sharing

シンプルなテキスト生成モデルを構築する

LlaMaを構築する前に、まずはシンプルなSeq2seqモデルを作成し、その後、この基本的なSeq2seqモデルにLlaMaのオペレータであるRMS、Rope、SwiGLUを順次追加していきます。最終的に完全なLlaMaモデルを構築します。

まずは、いくつかのユーティリティ関数を実装します。特に難しくはありませんが、一通り確認することをお勧めします。データの形状を頭の中でイメージしながら進めると、モデル構築の際に、どのような入力が処理されているのかを理解しやすくなり、ディープニューラルネットワークの理解に大いに役立ちます。

import

import torch
from torch import nn
from torch.nn import functional as F
import numpy as np
from matplotlib import pyplot as plt
import time
import pandas as pd
import urllib.request

上記は、使用する必要があるすべてのライブラリです。

次に、設定（config）を保存するための辞書を作成します。

  # config を格納する辞書を作成します。
MASTER_CONFIG = {
    # パラメータをここに配置
}

源氏物語のデータセットをダウンロード

# 源氏物語データセットをダウンロードする
url = "https://raw.githubusercontent.com/wooheum-xin/llama_form_zero_jp/main/02hahakigi.txt"
file_name = "The_Tale_of_Genji.txt"
urllib.request.urlretrieve(url, file_name)

データの読み込み

# データを読み出す
with open("The_Tale_of_Genji.txt", 'r', encoding='shift_jis', errors='replace') as f:
    lines = f.read()

# 簡易辞書の作成（文字レベル）
vocab = sorted(list(set(lines)))

# 最初のn文字を表示
head_num=50
print('最初の{}文字:'.format(head_num), vocab[:head_num])

print('サイズ:', len(vocab))

語彙を整数にエンコードする
通常の整数にエンコードします。例えば、"1":"あ"、"2":"い"、"3":"う"のように、次にキーと値を反転させたものも用意します。

# 辞書を数字、普通の整数にエンコードする
itos = {i: ch for i, ch in enumerate(vocab)}

# 双方向マッピング
stoi = {ch: i for i, ch in enumerate(vocab)}

次に、簡易なエンコーダとデコーダを作成します。これを使用して、モデルに入力する前にテキストを数値に変換し、出力する前に数値をテキストに変換します。

# エンコーダ
def encode(s):
    return [stoi[ch] for ch in s]

# デコーダ
def decode(l):
    return ''.join([itos[i] for i in l])

decode(encode("源氏"))
encode("源氏")
# [681, 645]

出力される2つの数字は、「源」字と「氏」字を表しており、これらはvocab語彙表の中でエンコードされています。これはエンコードマッピング表の原理です。

今回使用しているのは文字単位のエンコードであり、BPEや他の形式の語彙表構築ではありません。この部分は、tiktokenや他のマッピング手法に置き換えることもできますが、本記事では原理を理解することが主な目的なので、できるだけシンプルな方法を使用しています。そのほうが理解しやすいです。

# 全文を符号化し，tensorにマッピング
dataset = torch.tensor(encode(lines), dtype=torch.int16)

# 2.9万文字です
print(dataset.shape)
print(dataset)

上記のコードブロックでは、『源氏物語』全体をエンコードして、テンソルに変換しました。本記事では、2.9万文字以上を一つの1次元テンソルに変換しました。

次にバッチを構築します。

# batch の構築
def get_batches(data, split, batch_size, context_window, config=MASTER_CONFIG):
    # 分割訓練セット，検証セット，テストセット，比率は，訓練80%，検証10%，テスト10%である
    train = data[:int(0.8 * len(data))]
    val = data[int(0.8 * len(data)): int(0.9 * len(data))]
    test = data[int(0.9 * len(data)):]

    # すべての訓練データをbatch，検証セット，テストセットとしても変数ごとに格納する（単純に見るため）
    batch_data = train
    if split == 'val':
        batch_data = val
    if split == 'test':
        batch_data = test

    # ここでtorch.randintを学ぶ必要がある，サイズがbatch_sizeで内部値が乱数の整数であるtensorを生成する.乱数を生成する数値フィールドは、[0, トレーニングセット文字数 - スライドウィンドウサイズ- 1] の整数です。
    # 詳細は、公式文書を参照することができる
    ix = torch.randint(0, batch_data.size(0) - context_window - 1, (batch_size,))
    # print('ix:')
    # print(ix)


    # ここでtorch.stackを学ぶ必要がある, 実行操作はpythonのzipキーワードに似ているが，操作対象がtensorテンソルであるだけで，任意の次元のテンソルを指定して組み合わせる.
    # 詳細は、公式文書を参照することができる

    # ここで，xを素性，yを予測値とすると，文書生成タスクは上位n文字から下位1文字を推論するため，yの構造はウィンドウを元のサイズのまま1桁後ろに移動させる.
    # ウィンドウをスライドさせることにより，batch_data中の訓練データをランダムにサンプリングし，訓練データをランダムに選択することに相当する.
    # 元の約2.9万文字のうち，ランダムに1文字を開始点とし，その開始点から後方にスライドウィンドウの個数分の文字を選択し，訓練データとして後方に1桁移動させることが目標値である. したがってixの構造はindexを超えてはならない.
    x = torch.stack([batch_data[i:i+context_window] for i in ix]).long()
    y = torch.stack([batch_data[i+1:i+context_window+1] for i in ix]).long()

    # 固有値、目標値を戻します。
    return x, y

torch.randintやtorch.stackについては、一度学んでおくと良いです。このような記事はたくさんあります。

注目すべきは、以下の2行のコードです：

x = torch.stack([batch_data[i:i+context_window] for i in ix]).long()

y = torch.stack([batch_data[i+1:i+context_window+1] for i in ix]).long()

このコードでは、スライディングウィンドウの形式でデータの特徴値とターゲット値を取得しています。トレーニング時には、前のN文字を基に次の1文字を予測するため、ターゲット値yのスライディングウィンドウは、元のサイズ（長さ）を保持したまま右に1つシフトします。

# 上記で構築したget_batchs()関数に従って、パラメータ辞書を更新します。
MASTER_CONFIG.update({
    'batch_size': 8,
    'context_window': 8,
    'vocab_size':1087  # 源氏物語辞書のサイズ
})

辞書を作成して、configパラメータを保存します。例えば、スライディングウィンドウの値を16と設定すると、テキストをサンプリングする際に、各テキストを長さ16のデータに分割することを意味します。vocab_sizeは先ほどの説明にある通り、『源氏物語』のすべての文字を重複なしで集計した文字数、つまり語彙表のサイズを表します。

理解を深めるために、関数やクラスを構築するたびに、その都度実行して結果を確認しましょう。多くのコードを一度にまとめて実行すると、最終結果を見ても混乱する可能性があります。

したがって、先ほどのget_batches関数を実行して結果を確認します。観察を容易にするため、デコーダを使用して結果をデコードしてみます。

# トレーニングデータの取得
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])

# ランダムに生成されたサンプリングであるため、我々はデータを見ることができ、その中の各サンプリングデータは、原文のランダムな開始点から来て、各タプルは一つの（x、y）であり、各xとyの先頭を観察して、ウィンドウをスライドして実行する操作を直観的に感じることができる。
decoded_samples = [(decode(xs[i].tolist()), decode(ys[i].tolist())) for i in range(len(xs))]

print(decoded_samples)
# [('やみ》なことを言', 'み》なことを言う'), ('する人の直覚であ', 'る人の直覚であな'), ('ることができるは', 'ことができるはず'), ('置かれる程度のも', 'かれる程度のもの'), ('で置かず、気のき', '置かず、気のきい'), ('《じょうず》にこ', 'じょうず》にこし'), ('来客にも近づきま', '客にも近づきませ'), ('っていて、源氏が', 'ていて、源氏が行')]

出力結果はリストで、そのリストの要素は複数のタプルです。各タプルは特徴データとターゲット値を含んでいます。各タプルのデータの開始と終了を観察することで、スライディングウィンドウの効果を確認できます。

次に、評価関数を構築します。

# 評価関数の作成
@torch.no_grad()
def evaluate_loss(model, config=MASTER_CONFIG):
    # 評価結果ストレージ変数
    out = {}

    # モデルを評価モードに設定する
    model.eval()

    # 評価データはそれぞれ訓練セットと検証セットでget_batchs()関数で取得される
    for split in ["train", "val"]:

        losses = []

        # 10個のbatchを評価
        for _ in range(10):
            # 固有値（入力データ），および目標値（出力データ）を取得する.
            xb, yb = get_batches(dataset, split, config['batch_size'], config['context_window'])

            # 得られたデータをモデルに投げ込みloss値を得る.
            _, loss = model(xb, yb)

            # lossストレージの更新
            losses.append(loss.item())

        # これがコンソールでよく見られる「train_loss」「valid_loss」の由来です
        out[split] = np.mean(losses)

    # 評価が終わったので、模型を再び訓練状態に戻すことを忘れないで、次のepochは訓練を継続しなければならない。
    model.train()

    return out

ここまでの操作では、特に「目の前が真っ暗になる」ような難しい部分はなかったはずです。

ここで1つ区切りとして、特に大きな意味はありませんが、もし上記の内容を一通り確認し、jupyterやcolabで実行して問題がなければ、次に進んでください。

少し余談ですが、もし「このコードをすぐに使いたい」と考えているなら、この記事はそこまで万能ではないかもしれません（結局、『源氏物語』の原文2.9万字を使って、事前学習モデルなしで驚異的な大規模モデルが作れるわけではありません）。LLMを学びたいというのであれば、もう一度強調しますが、コードを一行ずつしっかり読んでください。そうしないと混乱して、余計に頭が痛くなるかもしれません。

---

LlaMaアーキテクチャの分析に入る前に、まず最もシンプルなテキスト生成モデルを作成し、その上にLlaMaのRSMやRopeなどを少しずつ追加していきます。これを実現するために、まず以下を行います：

1. 問題のある（不完全な）モデルアーキテクチャを作成

class StupidModel(nn.Module):
    def __init__(self, config=MASTER_CONFIG):
        super().__init__()
        self.config = config

        # エンベデッド·レイヤー、入力: 辞書サイズ、出力: 次元サイズ
        self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])

        # フィーチャーのリレーションにスナップする直線レイヤーを作成
        # LlaMaが使用している活性化関数はSwiGLUですが、現在この愚かなモデルアーキテクチャではまずReluを使用しています。

        self.linear = nn.Sequential(
            nn.Linear(config['d_model'], config['d_model']),
            nn.ReLU(),
            nn.Linear(config['d_model'], config['vocab_size']),
        )

        # このコマンドはモデルのパラメータ数を直接確認するのに役立ちます。
        # さもなければ自分で手計算するか、誰かが話す『7B』『20B』『108B』のようなモデルを聞くしかありませんが、このコマンドがあれば、あなたが作成したモデルのパラメータ数を直接確認できます。
        print("パラメータ数：", sum([m.numel() for m in self.parameters()]))

おそらく、コメントを見れば十分だと思います。まずは、少し"stupid"なモデルを作成しました。このモデルの構造は非常にシンプルで、埋め込み層、線形変換、活性化関数のみで構成されています。唯一面白い部分は、以下のコマンドです。これを覚えておけば、今後モデルのパラメータ数を調べるのに役立ちます。

print("パラメータ数:", sum([m.numel() for m in self.parameters()]))

次に、上記の"stupid"なモデルに前向き伝播（forward）関数を追加します。名前を変えて、「簡単な破損モデル」とでもしましょう。実際には"broken"が「問題がある」という意味ですが、その問題についてはすぐに説明します。

# 我々が作成した小さなモデルに前向き伝播を追加
class SimpleBrokenModel(nn.Module):
    # initの内容は上と同じで、変更なし
    def __init__(self, config=MASTER_CONFIG):
      super().__init__()
      self.config = config
      self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])
      self.linear = nn.Sequential(
          nn.Linear(config['d_model'], config['d_model']),
          nn.ReLU(),
          nn.Linear(config['d_model'], config['vocab_size']),
      )

      # 前向き伝播関数を追加
    def forward(self, idx, targets=None):
        # embedding層をインスタンス化し、IDにマッピングされたデータを入力して、埋め込み後のデータを出力
        x = self.embedding(idx)

        # embedding層の出力データを線形層に渡す
        a = self.linear(x)

        # 線形層の出力データに対して、最後の次元でsoftmaxを行い、確率分布を得る
        logits = F.softmax(a, dim=-1)

        # もしターゲット値（前述のy）がある場合は、クロスエントロピー損失を用いて損失を計算する。出力の確率マトリックスの形状を変え、ターゲット値の形状も変える。入力と出力を統一してから損失を計算する。最後の次元は1つのデータを表している。
        # ここで、tensor.view()関数を理解し、幾何学的な空間想像力でマトリックスの形状をイメージする必要がある。
        if targets is not None:

            loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
            return logits, loss

        # ターゲット値がない場合、確率分布の結果のみを返す
        else:
            return logits

        # パラメータ数を確認
        print("モデルのパラメータ数：", sum([m.numel() for m in self.parameters()]))

トレーニング段階だけでなく、推論（評価）段階についても記載されています。条件分岐でターゲット値が存在するかどうかを確認し、存在しない場合はモデルの出力結果のみを返します。ターゲット値が存在する場合は、出力結果に加えて損失（loss）値も返します。

# ここでは、このモデルのembeddingを128次元に設定
MASTER_CONFIG.update({
    'd_model': 128,
})

# モデルをインスタンス化し、引数を渡す
model = SimpleBrokenModel(MASTER_CONFIG)

# 再度パラメータ数を確認
print("パラメータ数:", sum([m.numel() for m in model.parameters()]))

埋め込み次元を128に設定します。LlaMaの埋め込み次元は4096ですが、今回はCPU上でトレーニングするため、小さめに設定します。この設定で、29万パラメータを持つモデルが得られます。

次に、トレーニング前のモデルの出力結果とlossを確認します。モデルの出力結果は数値ですが、lossを見るほうが分かりやすいでしょう。

# 訓練用の特徴データとターゲットデータを取得
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])

# モデルに投入して、確率分布マトリックスと損失を取得
logits, loss = model(xs, ys)
loss
# tensor(6.9912, grad_fn=<NllLossBackward0>)

次に、configのハイパーパラメータを更新し、モデルをインスタンス化してオプティマイザを設定します：

# パラメータを更新、訓練エポック数、バッチサイズ、ログ出力間隔を設定
MASTER_CONFIG.update({
    'epochs': 1000,
    'log_interval': 10,      # 10バッチごとにログを出力
    'batch_size': 32,
})

# モデルをインスタンス化
model = SimpleBrokenModel(MASTER_CONFIG)

# Adamオプティマイザを作成（基礎知識）
optimizer = torch.optim.Adam(
    model.parameters(),      # オプティマイザはモデルの全パラメータを最適化する
)

次に、トレーニング関数を構築してトレーニングを開始します：

# トレーニング関数を構築
def train(model, optimizer, scheduler=None, config=MASTER_CONFIG, print_logs=False):
    # 損失を保存
    losses = []

    # 訓練開始時間を記録
    start_time = time.time()

    # 指定されたエポック数分トレーニングを繰り返す
    for epoch in range(config['epochs']):
        # オプティマイザを初期化しないと、毎回の訓練が前回の結果を基に最適化され、効果がほとんどありません
        optimizer.zero_grad()

        # 訓練データを取得
        xs, ys = get_batches(dataset, 'train', config['batch_size'], config['context_window'])

        # 前向き伝播で確率マトリックスと損失を計算
        logits, loss = model(xs, targets=ys)

        # 逆伝播で重みパラメータを更新し、学習率の最適化器を更新
        loss.backward()
        optimizer.step()

        # もし学習率スケジューラが提供されていれば、スケジューラを使って学習率が変更されます。例えば、学習率が周期的に変化したり、勾配が減少・増加したりします。具体的な戦略は慎重に設定する必要があります。詳しくは「lr_scheduler」で検索してください。
        if scheduler:
            scheduler.step()

        # ログを出力
        if epoch % config['log_interval'] == 0:
            # 訓練時間を計算
            batch_time = time.time() - start_time

            # 評価関数を実行し、訓練セットと検証セットで損失を計算
            x = evaluate_loss(model)

            # 検証損失を保存
            losses += [x]

            # 進捗ログを出力
            if print_logs:
                print(f"Epoch {epoch} | val loss {x['val']:.3f} | Time {batch_time:.3f} | ETA in seconds {batch_time * (config['epochs'] - epoch)/config['log_interval'] :.3f}")

            # 次のエポックの訓練時間を計算するため、開始時間をリセット
            start_time = time.time()

            # 学習率スケジューラを使用している場合、次のエポックの学習率を出力
            if scheduler:
                print("lr: ", scheduler.get_lr())

    # 全エポックのトレーニングが終了し、最終結果を出力
    print("Validation loss: ", losses[-1]['val'])

    # 損失値のリストを返す。グラフを描画するため、損失の推移を返します。
    return pd.DataFrame(losses).plot()

# トレーニングを開始
train(model, optimizer)

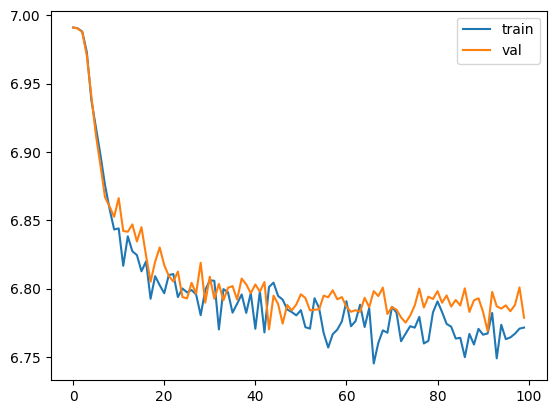
1000エポックのトレーニング後、loss値は元の6.99から6.77まで減少しました！

これで、なぜこのモデルアーキテクチャが「stupid」や「Broken」と呼ばれるのか分かりましたね。

*** でも！！！***

直せる！！

原因を分析しましょう：

上記のトレーニングフレームワークにはいくつか問題があります。前向き伝播（forward）のコードに戻ると、logits = F.softmax(a, dim=-1)で線形層の出力に対して確率分布を計算しています。しかし、lossの計算には交差エントロピー損失（cross entropy）を使用しており、ターゲット値は語彙にマッピングされた整数で、モデルの出力logitsは確率マトリックスです。

この2つを計算することは、国内の街で外国人に「Hey man, what's up?」と言ったら、相手が「日本語できますよ！」（日本語を話せるよ、どうしたの？）と答えるようなものです。理解はできるものの、収束させるのが少し面倒です。

lossの計算をより精密にするために、softmaxを取り除く必要があります。これにより、交差エントロピー損失の計算がより効果的になります。

# softmaxを取り除き、logitsを最後の線形層の出力結果として取得し、確率分布の計算を行わないようにします。
# そのため、このアーキテクチャを「それほど愚かではないモデルアーキテクチャ」と命名します。
class SimpleNotStupidModel(nn.Module):
    def __init__(self, config=MASTER_CONFIG):
      super().__init__()
      self.config = config
      self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])
      self.linear = nn.Sequential(
          nn.Linear(config['d_model'], config['d_model']),
          nn.ReLU(),
          nn.Linear(config['d_model'], config['vocab_size']),
      )
      print("モデルのパラメータ数:", sum([m.numel() for m in self.parameters()]))

    def forward(self, idx, targets=None):
        x = self.embedding(idx)

        # ここを見てください。線形層が直接結果を出力し、確率マトリックスに変換せず、この部分だけを変更します。他はそのままです。
        logits = self.linear(x)
        # print(logits.shape)

        if targets is not None:

            loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
            return logits, loss
        else:
            return logits
        print("モデルのパラメータ数:", sum([m.numel() for m in self.parameters()]))

ReRun!

# 再度、各種機能をインスタンス化し、もう一度トレーニングを開始
model = SimpleNotStupidModel(MASTER_CONFIG)
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
logits, loss = model(xs, ys)
optimizer = torch.optim.Adam(model.parameters())
train(model, optimizer)

# 損失がかなり減少した

次に推論関数を構築します：

データを入力する準備はしていませんので、学習用として、5つの0（語彙表でいうと改行符 '\n'）を使って推論します。改行符を開始点として、そこから20文字を推測するループを行います。

# 推論関数（出力結果の精度については気にしないでください。重みは保存されておらず、モデルの初期化によって生成されたランダムな数値で構成された行列を使って推論しています）
def generate(model, config=MASTER_CONFIG, max_new_tokens=20):
    # ランダムな数値を生成し、入力データとします。5行1列で、5つの文字を入力することを表します。この部分は他のランダムな数値に置き換えてテストすることができます。
    idx = torch.zeros(5, 1).long()
    print(idx[:, -config['context_window']:])
    for _ in range(max_new_tokens):
        # 推論時には、後ろのn個のトークンに依存するため、スライディングウィンドウを後ろから選び、入力データの最後のトークン数個を選択します。つまり、トークン数が超えた場合、入力をカットして最後の数個のトークンのみを選択します：idx[:, -config['context_window']:]
        logits = model(idx[:, -config['context_window']:])
        # print(logits.size())
        # モデル出力の結果をデコードします。ここでのlogits[:, -1, :]はやや抽象的です。実際には、最初の次元は入力の文字数、2番目の次元は時間ステップ、3番目の次元は語彙です。
        # 各ステップのデコード結果に対して、最後の時間ステップのデータを出力として取得します。デコードの過程は、1回目は5つのトークンを入力し、2回目は元の5つのトークンの最後の4つと前回のデコード結果で生成された1つのトークンを使い、再び5つのトークンでデコードします。このようにループしていきます。
        last_time_step_logits = logits[:, -1, :]
        # print('last_time_step_logits')
        # print(last_time_step_logits.shape)
        # 確率分布を計算
        p = F.softmax(last_time_step_logits, dim=-1)
        # print('p_shape')
        # print(p.shape)
        # 確率分布に基づいて次のトークンを計算します。ここでは torch.multinomial を使用してランダムサンプリングを行います。
        idx_next = torch.multinomial(p, num_samples=1)
        # print('idx_next_shape')
        # print(idx_next.shape)
        # 新しいidxをテンソルの結合でデコードシーケンスに追加
        idx = torch.cat([idx, idx_next], dim=-1)
    # 前に定義したデコード関数を使ってIDを文字に変換し、5行21列のデータを取得します。各入力文字から開始し、20個の文字を生成します。入力された5つの数値がすべて0であり、語彙内で0番目に該当するのは'\n'です。
    print(idx.shape)
    return [decode(x) for x in idx.tolist()]

generate(model)

出力結果は、予想通り期待通り、かなり悪い結果でした。

['\n\u3000あなって朝まそんしその夜のでいたから、',
 '\n\u3000も私は指《た。女であ、男の襖子《ちに臨',
 '\n「といてもですかはい縁の大事がお通ない官',
 '\n「父親のこと、自分にな時上手でよないるで',
 '\n\u3000中の姉のよう思うおどはとが物は紀伊守者']

OK、ここまでで簡単なSeq2seqモデルの構築は完了です。上記のコードを一度実行してみて、理解しながら、行ごとに自分で分析してみてください。もし分からない箇所があれば、shapeを出力してデータの形状がどのように変化しているかを確認してください。

ここまでの内容をしっかり理解できたら、次に進みます。本題に入り、上記のシンプルなモデルを基にして、LlaMaのオペレータを一つずつ追加していきます。オペレータを追加するたびに、その効果を確認していきましょう。

---

本篇スタート：

LlaMaのオペレータを先ほどの簡易モデルアーキテクチャに追加します。主に以下を含みます：

• RMS_Norm
• RoPE
• SwiGLU

RMSNormの概要

標準化（norm）とは、トレーニング中にテンソルを標準化する操作で、平均値と分散を計算してサンプルを正規化します。

この計算によって、データを平均が0、分散が1のデータに変換し、データが標準正規分布に従うようにします。

平均と分散を使ってデータの標準偏差を計算すると、データの外れ値を保持しながら異常な構造も維持することで、勾配が安定し、勾配消失や爆発の問題を軽減します。また、異常な構造を維持することで過学習も抑制され、汎化能力が向上します。

RMSNormの登場

RMSNormが登場する前は、バッチごとの標準化を行う「batch normalization」が広く使われていました。これは、バッチ全体をサンプルの集団として、平均と分散を計算します。

その後、各トークンの特徴ベクトルを正規化する「layer normalization」が登場しました（特徴ベクトルについては、以前の記事でRoPEについて説明しています。トークンと特徴ベクトルの関係が理解できるはずです）。layer normalizationでも平均と分散が必要です。

RMSNormとLayerNormの違い

RMSNormとlayer_normの主な違いは、RMSNormでは平均と分散の両方を計算する必要がなく、均方根（RMS）だけを計算すればよい点です。RMSNormは、layer_normとほぼ同じパフォーマンスを維持しながら、7%-64%の計算コストを節約できます。

RMSNormの計算式：

RMSNormの動作原理

1. RMSの計算: 入力された特徴（例えば、ニューロンの出力）に対して、そのRMS（Root Mean Square）値をまず計算します。
2. 正規化: 各特徴の値をそのRMS値で割り、データのスケールを調整して、平均を0、標準偏差を1にします。
3. スケーリングとシフト: 正規化の後、RMSNormでは通常、学習可能なパラメータ（スケール係数とバイアス）が導入されます。これにより、モデルは特定のタスクに適した特徴表現を学習できます。

RMSの基本的な説明はこの辺りで終了です。それでは、RMSNormモジュールの実装に移りましょう：

class RMSNorm(nn.Module):
    def __init__(self, layer_shape, eps=1e-8, bias=False):
        super(RMSNorm, self).__init__()

        # torchのregister_parameter()機能は、私たちが作成したネットワークモジュールにparameterを追加するためのものです。
        # そのため、pytorchの公式に用意されたRMSNorm機能モジュールに、訓練可能なパラメータの層を追加する必要があります。これをscaleと命名し、形状をlayer_shapeに初期化し、すべての値を1に設定したテンソルマトリックスとします。
        self.register_parameter("scale", nn.Parameter(torch.ones(layer_shape)))

    def forward(self, x):
        # Frobeniusノルム（行列のすべての要素の平方和の平方根を求めるノルムで、行列の大きさを測るために使用します。詳細は検索してください）。RMS = 1/sqrt(N) * Frobenius
        # 具体的には、torch.linalg.norm(x, dim=(1, 2))はxの第1および第2次元におけるノルムを計算します。その後、結果にx[0].numel() ** -.5を掛けます。x[0].numel()はxの最初の要素（つまりxの最初の行）の要素数を示し、** -.5は平方根の逆数を表します。
        ff_rms = torch.linalg.norm(x, dim=(1,2)) * x[0].numel() ** -.5
        # print(ff_rms.shape)
        # ff_rms演算子を入力テンソルxに適用し、式に基づいて除算を行います。入力ベクトルxは3次元なので、ff_rmsも2次元に拡張して3次元テンソルにします。これにより要素間の計算が可能になります。
        raw = x / ff_rms.unsqueeze(-1).unsqueeze(-1)
        # print(raw.shape)
        # scaleでスケーリングした正規化されたテンソルを返します。
        # print(self.scale[:x.shape[1], :].unsqueeze(0) * raw)
        return self.scale[:x.shape[1], :].unsqueeze(0) * raw

注意すべき点として、raw = x / ff_rms.unsqueeze(-1).unsqueeze(-1)の計算は、テンソルマトリックスの各要素に対して行われています。ここで計算されるのはノルムであり、これは実際には単なる数値で、マトリックスではありません。元の入力データのテンソルマトリックス内の各要素を、この正規化されたノルムで割っています。RMSNormはpytorchの公式nn.Moduleを継承しているため、少しだけ修正を加えています。

続いて、このRMS_Normオペレータを上記の簡易モデルに追加します。コードには、このオペレータをどのように組み込むかが明確に記載されています：

class SimpleNotStupidModel_RMS(nn.Module):
    def __init__(self, config=MASTER_CONFIG):
      super().__init__()
      self.config = config
      self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])
      # ここでRMS層を追加します
      self.rms = RMSNorm((config['context_window'], config['d_model']))
      self.linear = nn.Sequential(
          nn.Linear(config['d_model'], config['d_model']),
          nn.ReLU(),
          nn.Linear(config['d_model'], config['vocab_size']),
      )
      print("モデルのパラメータ数:", sum([m.numel() for m in self.parameters()]))

    def forward(self, idx, targets=None):
        x = self.embedding(idx)
        # ここで、RMS層のインスタンスを追加し、Embedding層の出力テンソルを受け取ります
        x = self.rms(x)

        logits = self.linear(x)
        # print(logits.shape)

        if targets is not None:

            loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
            return logits, loss
        else:
            return logits
        print("モデルのパラメータ数:", sum([m.numel() for m in self.parameters()]))

# さて、これで元のNotStupidModelにRMSNormを追加しました。さっそく実行してみましょう
model = SimpleNotStupidModel_RMS(MASTER_CONFIG)

xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])

logits, loss = model(xs, ys)

optimizer = torch.optim.Adam(model.parameters())

train(model, optimizer)

# 同じ訓練ハイパーパラメータ設定で、RMSNormを追加すると訓練速度が明らかに速くなりました。

もしコードを実行した場合、計算速度が速くなったことを感じるかもしれません。

ですが、急がないでください。次の2つのオペレータは計算速度をさらに遅くするでしょう(笑)。

回転位置エンコーディング（RoPE）をモデルに追加。

RoPEは、デカルト座標系での計算を極座標空間に移行するという巧妙な方法です。

まず、回転位置エンコーディングを計算するための関数を定義します：

def get_rotary_matrix(context_window, embedding_dim):
    # 形状が（context_window, embedding_dim, embedding_dim）のゼロで埋められたテンソルマトリックスを初期化します。context_windowはトークン数を表し、後ろの2つのembedding_dimは正方行列を構成し、後でattention計算の形式に合わせます。
    R = torch.zeros((context_window, embedding_dim, embedding_dim), requires_grad=False)

    # 各位置のトークンを繰り返し処理します
    for position in range(context_window):
        # 私の前回の記事で述べたように、特徴量は2つずつ組み合わせる必要があるため、ループの回数はembedding_dimを2で割った数になります。
        for i in range(embedding_dim // 2):
            # θ値、サンプリング周波数、または回転周波数や回転角度を設定します。embedding_dimで割ることで勾配問題を防ぎます。
            theta = 10000. ** (-2. * (i - 1) / embedding_dim)
            # オイラーの公式に基づいて回転角度を計算し、それぞれsinとcosを使用して、計算結果を複素数空間に引き込み、回転角度を上記のゼロで埋められたマトリックスに適用します。
            m_theta = position * theta
            R[position, 2 * i, 2 * i] = np.cos(m_theta)
            R[position, 2 * i, 2 * i + 1] = -np.sin(m_theta)
            R[position, 2 * i + 1, 2 * i] = np.sin(m_theta)
            R[position, 2 * i + 1, 2 * i + 1] = np.cos(m_theta)
            # 得られた結果は回転位置エンコーディングマトリックスです。ここではまだattentionには関わっていません。
    return R

回転位置エンコーディング（RoPE）は注意機構のQとKを組み合わせて計算されるため、まず単一のヘッドを持つ注意機構のオペレータを実装します：

# これは単一のヘッドを持つ注意機構です
class RoPEMaskedAttentionHead(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        # Q重み行列を計算
        self.w_q = nn.Linear(config['d_model'], config['d_model'], bias=False)
        # K重み行列を計算
        self.w_k = nn.Linear(config['d_model'], config['d_model'], bias=False)
        # V重み行列を計算
        self.w_v = nn.Linear(config['d_model'], config['d_model'], bias=False)
        # 回転位置エンコーディング行列を取得し、次にQとKの重み行列を上書きします
        self.R = get_rotary_matrix(config['context_window'], config['d_model'])


    # ここで、前のコードブロックで実装された回転位置エンコーディングの作成機能をそのまま使用します
    def get_rotary_matrix(context_window, embedding_dim):
        # 形状が（context_window, embedding_dim, embedding_dim）のゼロで埋められたテンソルマトリックスを初期化します。context_windowはトークン数を表し、後ろの2つのembedding_dimは正方行列を構成し、後でattention計算の形式に合わせます。
        R = torch.zeros((context_window, embedding_dim, embedding_dim), requires_grad=False)

        # 各位置のトークンを繰り返し処理します
        for position in range(context_window):
            # 私の前回の記事で述べたように、特徴量は2つずつ組み合わせる必要があるため、ループの回数はembedding_dimを2で割った数になります。
            for i in range(embedding_dim // 2):
                # θ値、サンプリング周波数、または回転周波数や回転角度を設定します。embedding_dimで割ることで勾配問題を防ぎます。
                theta = 10000. ** (-2. * (i - 1) / embedding_dim)
                # オイラーの公式に基づいて回転角度を計算し、それぞれsinとcosを使用して、計算結果を複素数空間に引き込み、回転角度を上記のゼロで埋められたマトリックスに適用します。
                m_theta = position * theta
                R[position, 2 * i, 2 * i] = np.cos(m_theta)
                R[position, 2 * i, 2 * i + 1] = -np.sin(m_theta)
                R[position, 2 * i + 1, 2 * i] = np.sin(m_theta)
                R[position, 2 * i + 1, 2 * i + 1] = np.cos(m_theta)
                # 得られた結果は回転位置エンコーディングマトリックスです。ここではまだattentionには関わっていません。
        return R

    def forward(self, x, return_attn_weights=False):
        # 前方伝播時、入力マトリックスの形状は(batch, sequence length, dimension)です。

        b, m, d = x.shape  # バッチサイズ、シーケンス長、次元

        # Q, K, Vの線形変換を行います
        q = self.w_q(x)
        k = self.w_k(x)
        v = self.w_v(x)

        # 回転位置エンコーディングをQとKに適用します。ここでtorch.bmmは行列の外積を行い、transposeは転置を行います。Q行列を転置し、回転位置エンコーディングと外積を取り、元に戻します。これにより、Qに回転位置エンコーディングが適用されます。
        # 入力テキストの長さを考慮して、位置エンコーディング行列の第1次元を切り捨てます。長すぎても意味がないため、テキスト長と同じにします。
        q_rotated = (torch.bmm(q.transpose(0, 1), self.R[:m])).transpose(0, 1)
        # 同様にKにも回転位置エンコーディングを適用して上書きします
        k_rotated = (torch.bmm(k.transpose(0, 1), self.R[:m])).transpose(0, 1)

        # 注意機構の内積に対してスケーリングを行い、attentionテンソルが長くなりすぎて勾配爆発が起きるのを防ぎます
        activations = F.scaled_dot_product_attention(
            q_rotated, k_rotated, v, dropout_p=0.1, is_causal=True
        )
        # return_attn_weightsが1に設定されている場合、attentionにマスクを適用します。これは、モデルが前のn個のトークンに基づいて次のトークンを予測するように学習させるためで、カンニングのようなことを避けます。
        if return_attn_weights:
            # 注意マスク行列を作成します。torch.tril関数は、行列に対して左下三角部分を取得し、それ以外の部分を0にします。
            attn_mask = torch.tril(torch.ones((m, m)), diagonal=0)
            # 注意機構の重み行列を計算し、最後の次元に沿って正規化します。（突撃チェック）なぜ最後の次元なのか？それは最後の次元が各トークンの特徴ベクトルを表しているからです！
            attn_weights = torch.bmm(q_rotated, k_rotated.transpose(1, 2)) / np.sqrt(d) + attn_mask
            attn_weights = F.softmax(attn_weights, dim=-1)
            return activations, attn_weights

        return activations

単一の注意機構のヘッドが実装完了したので、次にマルチヘッド注意機構を実装します

# 単一の注意機構のヘッドが実装完了したので、次にマルチヘッド注意機構を実装します
class RoPEMaskedMultiheadAttention(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        # 注意機構のヘッドオブジェクトを1つ作成したので、次にマルチヘッドを実装します。複数の注意機構のヘッドを作成し、リストに入れます。
        self.heads = nn.ModuleList([
            RoPEMaskedAttentionHead(config) for _ in range(config['n_heads'])
        ])
        # モデル構造上、線形層（隠れ層）を作成し、注意機構のヘッドの出力テンソルマトリックスを線形出力します。これは、マルチヘッド間の特徴を探るためですが、主にxがマルチヘッド計算を経て形状が変わるため、テンソルマトリックスを元の形状に戻すために作成されます。
        # 同時に、過学習を防ぐために、ドロップアウト（0.1の割合でランダムにニューロンを無効化）を使用します。
        # 線形層の入力形状は、注意機構のヘッド数にマトリックスの次元数を掛けたもので、私の前回の記事で述べたように、keyマトリックスはマルチヘッド間で重みを共有し、計算量を削減します。出力はモデルの埋め込み次元数になります。
        self.linear = nn.Linear(config['n_heads'] * config['d_model'], config['d_model'])
        self.dropout = nn.Dropout(0.1)

    def forward(self, x):
        # 入力マトリックスの形状x: (batch, sequence length, dimension)

        # 各注意機構のヘッドにxを渡して計算します。（ここを並列実行すると速くなるかもしれませんが、pytorchが自動で並列実行するかは不明です）
        heads = [h(x) for h in self.heads]
        # 入力テンソルxは複数のヘッドでattention計算を行い（同時にattentionにはRoPEが適用されています）、新しいマトリックスとして再度結合し、変数xに戻します。この時点で、マトリックスの形状が変わったことに気づくはずです。
        x = torch.cat(heads, dim=-1)

        # ここで線形層の出番です
        x = self.linear(x)

        # ドロップアウトでランダムにニューロンを無効化し、過学習を防ぎます
        x = self.dropout(x)
        return x

これで上記の機能が実装できましたので、configのハイパーパラメータを更新して注意機構のヘッド数を設定しましょう。LlaMaでは32個の注意機構ヘッドがありますが、今回は8個に設定します：

# Llamaには32個の注意機構ヘッドがありますが、ここでは8個にしてみましょう

MASTER_CONFIG.update({
    'n_heads': 8,
})

次に、以前にRMS_Normを追加したモデルを更新します。今回はそれに加えて、ROPE位置エンコーディングを組み込んだマルチヘッド注意機構も追加します！

# 必要なオペレータをすべて作成しました。積み木は完成しましたので、これらを組み合わせていきましょう！！！
class RopeModel(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config

        # Embedding層
        self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])

        # RMSNorm層
        self.rms = RMSNorm((config['context_window'], config['d_model']))

        # 回転位置エンコーダ + 注意機構
        self.rope_attention = RoPEMaskedMultiheadAttention(config)

        # 線形層 + 活性化関数で非線形出力に変換！
        self.linear = nn.Sequential(
            nn.Linear(config['d_model'], config['d_model']),
            nn.ReLU(),
        )

        # 最終出力。デコードが必要で、出力の次元が語彙サイズと一致する必要があります！！！
        self.last_linear = nn.Linear(config['d_model'], config['vocab_size'])

        print("モデルのパラメータ数:", sum([m.numel() for m in self.parameters()]))

    # 前向き伝播
    def forward(self, idx, targets=None):
        # Embedding
        x = self.embedding(idx)
        # 正規化
        x = self.rms(x)
        # 足し算。attentionは元のマトリックスに適用されるため、形状が同じ2つのマトリックスがあると考えてください。左手に1枚の紙、右手にもう1枚の紙があり、両手を合わせて「パッ！」と重ねます。加算を使うことで、2つのマトリックスの要素が位置ごとに加算され、値が上書きされます！
        x = x + self.rope_attention(x)
        # 再度正規化！
        x = self.rms(x)
        # 直接正規化された値を計算すると勾配問題が発生する可能性があるため、正規化された値を補正係数として再度上書きします！
        x = x + self.linear(x)
        # ここでようやく最終的にvocab数のニューロン出力が得られます！！！！！！
        logits = self.last_linear(x)

        # 訓練段階ではターゲット値がある場合
        if targets is not None:
            loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
            return logits, loss
        # 検証や推論段階では、ターゲット値（y）がないため、結果だけが得られ、lossは計算されません！
        else:
            return logits

# 再度実行してみましょう！
model = RopeModel(MASTER_CONFIG)
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
logits, loss = model(xs, ys)
optimizer = torch.optim.Adam(model.parameters())
train(model, optimizer)

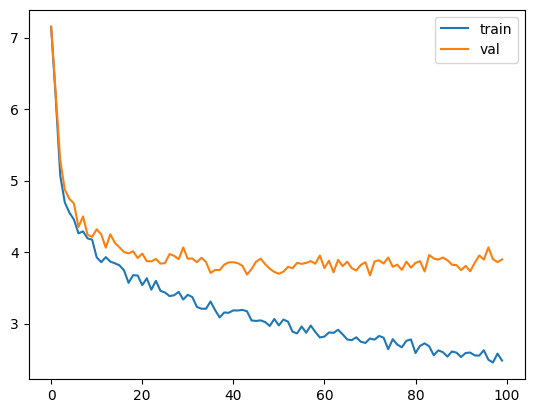
ええと、実際にはattentionのマスクが設定されていない状態です。機能は実装されていますが、呼び出されておらず、ブール値はfalseに設定されています。

SwiGLUの実装

swishとgluを組み合わせます。これらの活性化関数はそれぞれ単独でも非常に強力ですが、組み合わせることでさらに効果が発揮されます。

この組み合わせは少し神秘的なところがあります。良くないと言う人もいますが、確かにSwiGLUはReLUよりも多くの意味的特徴を保持し、ReLUのように突然小さな値になることで重要な特徴が消えてしまうことが少ないです。ただし、計算量がかなり大きいのも事実です。

swishはsigmoidを使い、GLUはゲート構造を使います（ゲート構造のアイデアは、RNN, GRU, LSTMなどを学ぶとよく理解できるでしょう）。

class SwiGLU(nn.Module):

    def __init__(self, size):
        super().__init__()
        # ゲート付き線形層を定義し、入力と出力はどちらもゲート構造のサイズです
        self.linear_gate = nn.Linear(size, size)
        # ゲート構造のメインの線形層
        self.linear = nn.Linear(size, size)
        # ランダムな数値をベータ係数として初期化
        self.beta = torch.randn(1, requires_grad=True)

        # nn.Parameterは、ある層のパラメータを学習可能にするために使用されます。本来は訓練によって変更されないパラメータを、訓練を通じて更新できるようにします。
        self.beta = nn.Parameter(torch.ones(1))
        # ランダムな数値betaを「beta」という名前のニューラルネットワーク層に指定します
        self.register_parameter("beta", self.beta)

    def forward(self, x):
        # Swishゲートの計算：（括弧内から計算を始めます）元の入力データテンソルは線形変換され、ベータ係数が掛けられ、次にsigmoid変換によって0から1の値に変換されます。その後、元のデータがゲート付き線形変換を通り、最終的に両者が掛け合わされます。つまり、線形出力が非線形変換され、その結果が線形変換の出力に適用されます。このプロセスでは、要素ごとに位置を合わせて掛け合わせ、元のデータテンソルを修正するのがゲート構造の役割です。
        swish_gate = self.linear_gate(x) * torch.sigmoid(self.beta * self.linear_gate(x))
        # ゲート構造の出力を線形出力の元データテンソルに再度掛け合わせます
        # なぜこうするのかは分かりませんが、論文の再現コードではこのように実装されています。興味があれば調べてみてください。
        out = swish_gate * self.linear(x)
        return out

先ほど定義したSwiGLUオペレータをモデルに追加します。このモデルには、すでにRMS RopeAttentionを追加しています。

# SwiGLUを上記のモデルに追加します
class RopeModel(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])
        self.rms = RMSNorm((config['context_window'], config['d_model']))
        self.rope_attention = RoPEMaskedMultiheadAttention(config)
        self.linear = nn.Sequential(
            nn.Linear(config['d_model'], config['d_model']),
            # ここで、SwiGLU層を追加しました
            SwiGLU(config['d_model']),
        )
        self.last_linear = nn.Linear(config['d_model'], config['vocab_size'])
        print("モデルのパラメータ数:", sum([m.numel() for m in self.parameters()]))

    def forward(self, idx, targets=None):
        x = self.embedding(idx)
        x = self.rms(x)
        x = x + self.rope_attention(x)
        x = self.rms(x)
        x = x + self.linear(x)
        logits = self.last_linear(x)

        if targets is not None:
            # ターゲットが提供されている場合、クロスエントロピー損失を計算します
            loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
            return logits, loss

        else:
            return logits

model = RopeModel(MASTER_CONFIG)
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
logits, loss = model(xs, ys)
optimizer = torch.optim.Adam(model.parameters())
train(model, optimizer)

ここまでで、追加できるオペレータはすべて追加しました。しかし、これはLlamaの1つの機能ブロックに過ぎません。Llamaは複数の機能ブロックを積み重ねて構成されています。

---

上記でLlaMaに必要なオペレータを実装しましたので、次にそれらを組み合わせてLlaMaの機能ブロックを作成し、その機能ブロックを積み重ねてLlaMaを構築します！

まず、機能ブロックの積み重ねる層数を設定します：

# OK！ では、隠れ層の次元を更新して、何層積み重ねるか決めましょう。まずは4層で試してみます！！
MASTER_CONFIG.update({
    'n_layers': 4,
})

次に、LlaMaの機能ブロックを作成します。実際には、RMS、AttentionRoPE、SwiGLU活性化関数を統合した簡易モデルを使用します：

# これで、すべてのオペレータ（RMS, ROPE, SWIGLU）を揃えましたので、LlaMaを構築します！ まず、LlaMaの基本ブロックを実装し、これを積み重ねます。
# 機能については特に説明することはありません。ここまでしっかり理解できた方なら、以下のコードは難しくないはずです。
class LlamaBlock(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.rms = RMSNorm((config['context_window'], config['d_model']))
        self.attention = RoPEMaskedMultiheadAttention(config)
        self.feedforward = nn.Sequential(
            nn.Linear(config['d_model'], config['d_model']),
            SwiGLU(config['d_model']),
        )

    def forward(self, x):
        x = self.rms(x)
        x = x + self.attention(x)

        x = self.rms(x)
        x = x + self.feedforward(x)
        return x

作成した機能ブロックに問題がないかテストしてみましょう：

# config辞書を使って、Llamaの基本ブロックを作成
block = LlamaBlock(MASTER_CONFIG)

# ランダムなデータを生成し、このLlamaブロックに投入してバグがないか確認
random_input = torch.randn(MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'], MASTER_CONFIG['d_model'])

# 実行して出力を確認
output = block(random_input)
output.shape

組み立て!!

# では、LlaMaを組み立てます
from collections import OrderedDict
class Llama(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        # Embeddingは説明不要
        self.embeddings = nn.Embedding(config['vocab_size'], config['d_model'])
        # 指定された層数に基づいてLlamaのブロックを作成します。OrderedDictは特殊な辞書型で、データの挿入順序が保持されます。先に挿入されたデータが前に、後に挿入されたデータが後になります。
        # ここではLlamaのブロックを4層積み重ねます
        self.llama_blocks = nn.Sequential(
            OrderedDict([(f"llama_{i}", LlamaBlock(config)) for i in range(config['n_layers'])])
        )
        # FFN層には、線形層、活性化関数で非線形変換を行い、再度線形層で最終的なデコード値を出力します。
        self.ffn = nn.Sequential(
            nn.Linear(config['d_model'], config['d_model']),
            SwiGLU(config['d_model']),
            nn.Linear(config['d_model'], config['vocab_size']),
        )

        # 大きなモデルのパラメータ数を確認します！
        print("モデルのパラメータ数:", sum([m.numel() for m in self.parameters()]))

    def forward(self, idx, targets=None):
        # embeddingに変換
        x = self.embeddings(idx)
        # Llamaモデルの計算
        x = self.llama_blocks(x)
        # FFNの計算を行い、logitsを取得
        logits = self.ffn(x)

        # 推論段階ではターゲット値がなく、結果のみを出力
        if targets is None:
            return logits
        # 訓練段階ではターゲット値があり、結果とlossを出力して逆伝播で重みを更新
        else:
            loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
            return logits, loss

# Llamaのトレーニングを開始します
llama = Llama(MASTER_CONFIG)
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
logits, loss = llama(xs, ys)
optimizer = torch.optim.Adam(llama.parameters())
train(llama, optimizer)

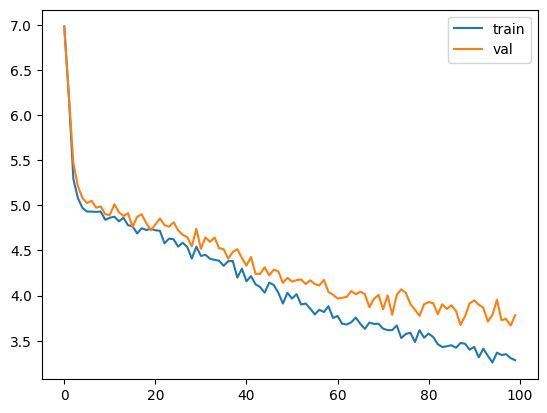
テストセットを実行

# これからテストセットを実行してみましょう
# テストセットの特徴量とターゲット値を取得
xs, ys = get_batches(dataset, 'test', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])

# Llamaに投入して損失を取得
logits, loss = llama(xs, ys)

print(loss)
# 5.0037！

最適化!!

# 最適化するポイントはまだありますよ、optimizerや学習率スケジューラを忘れないで！
# パラメータを調整して再度実行しましょう！

MASTER_CONFIG.update({
    "epochs": 1000
})

# 学習率最適化はコサインアニーリングを選択
llama_with_cosine = Llama(MASTER_CONFIG)

llama_optimizer = torch.optim.Adam(
    llama.parameters(),
    betas=(.9, .95),
    weight_decay=.1,
    eps=1e-9,
    lr=1e-3
)
# コサインアニーリング学習率スケジューラを使い、学習率を徐々に減少させ、最後には最小値に到達します。詳細は検索すればたくさんの記事が見つかります。
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(llama_optimizer, 300, eta_min=1e-5)

# 実行！
train(llama_with_cosine, llama_optimizer, scheduler=scheduler)

---

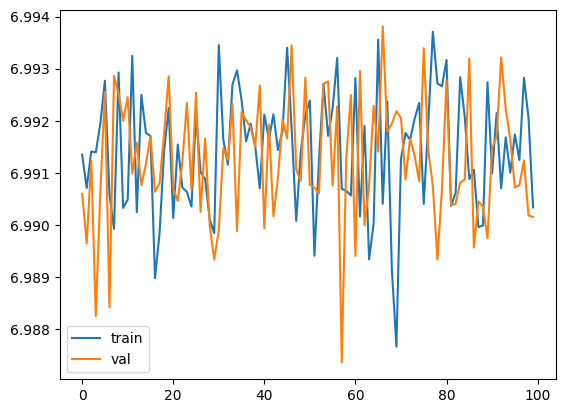
おめでとうございます！ここまで進んだあなたは、ついに自分だけのAIモデル（使えないけど）を作り上げました！

そうですね、基本的にはこれで完成です。主な部分ができれば、あとは戦略部分や他のオペレータを追加するだけで、構造さえ守れば何でも可能です。注目すべきは、入力と出力です。マトリックスの計算には数学の知識が必要で、要素ごとの計算なのか、それともベクトルやマトリックス全体の計算なのかを区別する必要があります。

ここまで読んで、上記の内容をほぼ理解できたのであれば、次に紹介する**llama3の公式モデルコード（model.py）**も容易に把握できると思います。Metaチームのコードは本当に全世界の人が理解できるように作られており、その整然とした構造と強力な説明性には感動します。大規模モデルを学習するのに最適なコードです。