3D Convolution 完全征服: Using PyTorch Conv3D
今日は3D Convolutionについて説明したいと思います。VoxelNet論文のレビューをしていて、3D Convolutionの概念を初めて目にしたのですが、PyTorchで実装されたConv3D関数の使い方を身につけたら、3D Convolution演算が何なのかもうわかりました!
3D Convolutionの基本的なRule
まず、3D Convolutionの基本的なRule4つを勉強します。
Rule Number One
はじめのルールです。 「3次元スケールのカーネルが3次元空間を巡回する」これはどういう意味? 下の図を見てください。
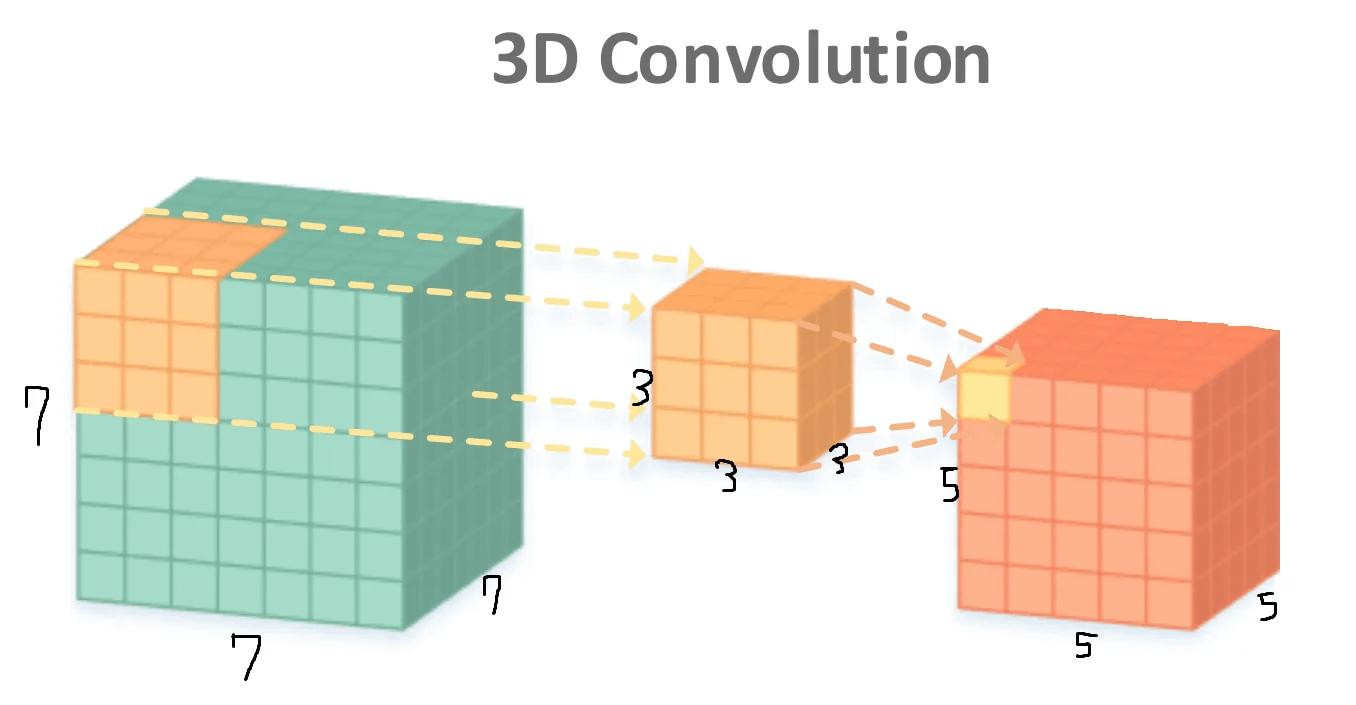
入力テンソルは7 x 7 x 7、カーネルは3 x 3 x 3、出力結果は5 x 5 x 5 サイズのテンソルです。 入力テンソルにカーネルが適用され、Element-wise乗算を経ると、計27個の(3x3x3)元素が生成されます。 これをすべて加えてBiasまで加えた結果が出力テンソルに黄色の部分です。
2D Convolutionと異なり、3D Convolutionではカーネルが(x, y, z)方向に巡回します。 上の図では、5 x 5 x 5 サイズの出力結果は(1, 1, 1)のStrideで、カーネルが入力テンソル空間を1マスずつ動かして生成されたものです。
そして、3D ConvolutionにもPaddingが存在します。 ダウンジャケットも(x、y、z)方向に与えることができます。 上記の例題では、Paddingを(0,0,0)にしたと考えればいいです。
Rule Number Two
2つ目のルールです。 「一つのフィルターはただ一つのBias値だけ持つ。」 上の図では、一つのフィルターが存在します。 あのフィルターには一つのBias値だけが存在するという話です。 もしフィルターが2つなら、2つのBiasが存在しますよね?
Rule Number Three
3つ目のルールです。 「3D Convolutionの出力チャンネルはフィルターの個数と同じです。」 急にチャンネルの話が出てきて戸惑いましたよね? 上図では、入力、出力テンソルのチャネルがすべて 1 の場合です。 しかし、実際に3D Convolution演算を使用すると、チャンネルが1の場合はほとんどありません。
Rule Number Four
最後のルールです。 「3D Convolutionの入力チャンネルはカーネルのチャンネルと同じだ。」 これも一応暗記してください! 以下で詳しくご説明します! (カーネルとは、一つのConvolutional Layerで使用されるフィルターの集合を意味します。 何かよく分からなければ、一応"フィルター=カーネル"と暗記されても構いません。)
PyTorch Conv3Dで3D Convolutionを理解
それでは実習を通じて3D Convolutionを説明します。 4つの例題を見てみましょう。 4つの例題は以下の通りです。

例題1
最初の例は、入力チャネルと出力チャネルが 1 の状況です。 この時、入力テンソルは4 x 4 x 4、そしてフィルターは2 x 2 x 2 サイズに設定します。 これを絵で描くと以下のようになります。
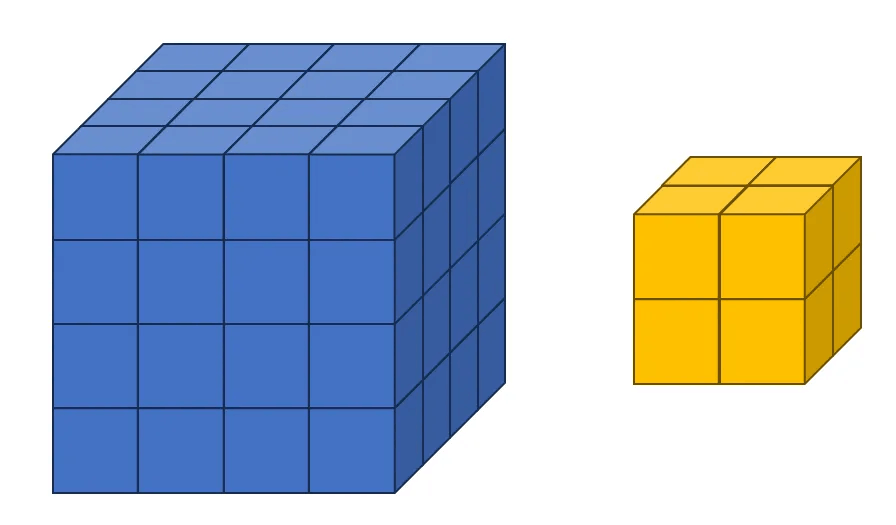
入力テンソルを作成します。 入力テンソルは、チャネルが 1 の 4 x 4 x 4 サイズのテンソルです。 以下のコードを実行してください。
tensor1 = torch.randint(0, 3, (1, 1, 4, 4, 4))
tensor1 = tensor1.float()
print(tensor1.shape)
print(tensor1)
上のコードの最初の行は、0から3未満の任意の数字でテンソルを作るようにという命令です。 そして後ろの(1、1、4、4、4)は順番にBatchの大きさ、チャンネル数、D、H、Wを意味します。 DはDepth、HはHeight、WはWidthです。
そして2列目ではテンソルをfloat型に変換します。 整数型のデータはConv3D関数に使用できないため、float型に型変換を進めたのです。
以下は実行結果です。 これは皆さんの結果と違うでしょう。
torch.Size([1, 1, 4, 4, 4])
tensor([[[[[2., 2., 0., 1.],
[1., 2., 0., 0.],
[1., 2., 0., 0.],
[0., 0., 0., 2.]],
[[0., 1., 1., 1.],
[2., 1., 1., 2.],
[0., 0., 1., 1.],
[0., 1., 0., 1.]],
[[1., 2., 2., 2.],
[2., 0., 2., 2.],
[1., 0., 1., 0.],
[2., 2., 2., 1.]],
[[0., 1., 1., 0.],
[0., 0., 0., 2.],
[0., 1., 2., 2.],
[2., 2., 2., 0.]]]]])
では、3D Convolution Layerを一つ作ってあげましょう。
conv1 = torch.nn.Conv3d(in_channels=1, out_channels=1, kernel_size=2, stride=1, padding=0)
print(conv1.weight)
print(conv1.bias)
入力チャンネルは1、出力チャンネルは1と言いました。 フィルターの大きさを2としましたが、これは(2、2、2)と同じ意味です。 もし、x、y、z軸でフィルターの大きさを異なるように設定したい場合は、(2、2、2)内の数字を変更すればいいです。 そしてStrideは1と言いましたが、これは(1、1、1)を意味します。 パディングは 0 になっていますが、これは (0, 0, 0) と同じです。
以下は出力の結果です。 これも皆さんと違うと思います。
Parameter containing:
tensor([[[[[-0.0627, -0.1470],
[ 0.0166, 0.2616]],
[[ 0.0281, -0.2612],
[-0.1522, 0.2398]]]]], requires_grad=True)
Parameter containing:
tensor([-0.0330], requires_grad=True)
それでは、3D Convolutionを実行してみましょう。
F1 = conv1(tensor1)
print(F1)
出力結果は以下の通りです。
tensor([[[[[ 0.1813, 0.4916, 0.4171],
[ 0.4908, -0.4211, 0.6465],
[-0.1391, 0.4759, 0.6968]],
[[ 0.0085, -0.4518, 0.3557],
[ 0.2341, -0.7259, -0.3750],
[ 0.4927, -0.5555, -0.3557]],
[[-0.3793, 0.9671, 1.1267],
[-0.7086, -0.1928, -0.0111],
[-0.1083, 0.4065, -0.1682]]]]], grad_fn=<ConvolutionBackward0>)
3 x 3 x 3 サイズの結果が出ました。 出力テンソルの一つの元素がどのような過程を経て計算されたのか見てみましょう。 F1[0][0][0][0]=-0.2383がどのように出たのか見てみましょう。

上記の図を拡大してご確認ください。青が入力テンソル、黄色がフィルター、赤が出力結果を表しています。黄色のテンソルの右上にもう1つの値がありますが、これはバイアス(Bias)です。このとき、2 × 2 × 2 のサイズのフィルターが入力テンソルの 2 × 2 × 2 部分に重なり、要素ごとの積(Element-wise product)を行います。実際に要素ごとの積を計算し、バイアスを加えた結果は以下の通りです。Excel で計算しました。
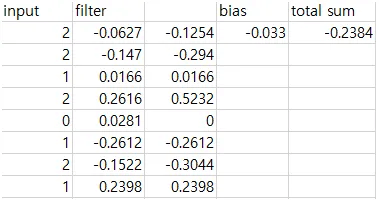
実際の値と 0.0001 の差があります。なぜこうなるのかは分かりません(笑)。いずれにしても、このようにして計算が進むことが分かります。これで理解できましたか?
例題2
2つ目の例では、入力チャネルが1、出力チャネルが2の状況です。入力テンソルは 4 × 4 × 4、フィルターは 2 × 2 × 2 のサイズに設定します。この場合の図は以下の通りです。今回はフィルターが2つあることがわかります。「Rule Three」を覚えていますか?フィルターの数は出力チャネルの数と同じです。したがって、オレンジ色がフィルター1、黄色がフィルター2を示しています。
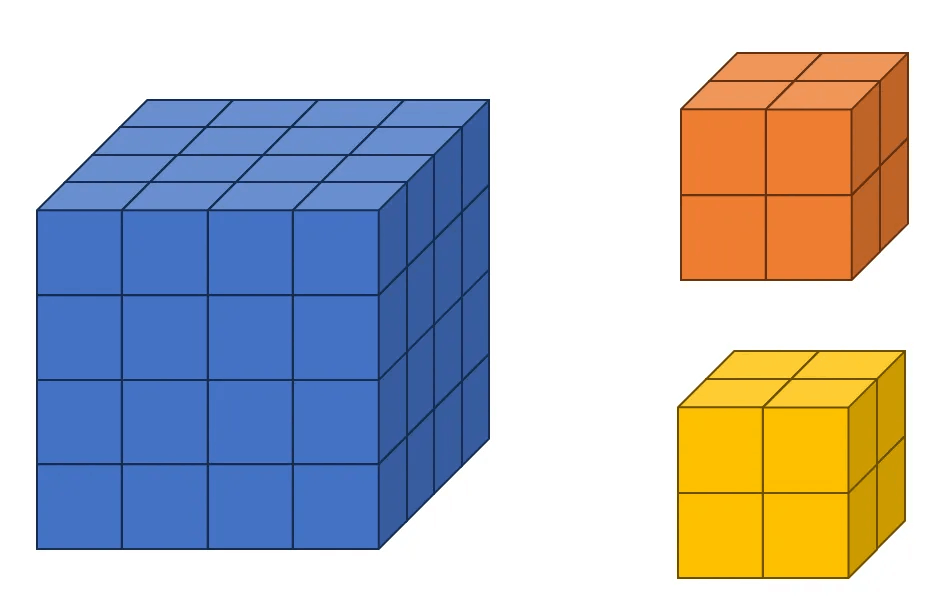
次に、コードの実装を始めます。例1で使用した入力テンソル tensor1 を引き続き使用します。以下のコードを新たに入力してください。
conv2 = torch.nn.Conv3d(in_channels=1, out_channels=2, kernel_size=2, stride=1, padding=0)
print(conv2.weight)
print(conv2.bias)
例1との違いは、出力チャネルのサイズが2に変更された点です。以下は実行結果です。
Parameter containing:
tensor([[[[[-0.1769, 0.0459],
[ 0.1724, -0.1089]],
[[-0.2235, 0.1996],
[ 0.1378, -0.1023]]]],
[[[[ 0.1983, 0.3071],
[ 0.0551, 0.0199]],
[[ 0.0893, -0.1499],
[ 0.1560, -0.0255]]]]], requires_grad=True)
Parameter containing:
tensor([0.0480, 0.1283], requires_grad=True)
フィルターが2つ出力されました。フィルターが2つあれば、当然バイアスも2つ存在します。そのため、それぞれのバイアスは 0.0480 と 0.1283 です。
では、3D畳み込み演算を実行してみましょう。
F2 = conv2(tensor1)
print(F2)
以下は実行結果です。
tensor([[[[[ 0.1136, 0.0508, 0.0032],
[-0.3298, -0.0871, 0.2593],
[-0.1395, 0.0317, -0.2960]],
[[ 0.7813, -0.2718, -0.1051],
[-0.5690, 0.1050, 0.1165],
[-0.2134, 0.5369, -0.2420]],
[[ 0.5073, -0.4556, -0.5151],
[-0.2356, -0.0360, 0.4286],
[ 0.2688, 0.4677, 0.3351]]],
[[[ 1.3708, 0.7052, 0.4799],
[ 1.0644, 0.5491, 0.0484],
[ 0.9153, 0.5311, 0.0820]],
[[ 0.6672, 0.5366, 0.8686],
[ 1.1666, 0.3284, 1.0507],
[ 0.4986, 0.6018, 1.0295]],
[[ 0.9012, 1.1183, 1.3275],
[ 0.5546, 0.8675, 1.1556],
[ 0.5880, 0.6361, 0.6477]]]]], grad_fn=<ConvolutionBackward0>)
結果を見ると、3 × 3 × 3 のサイズの出力が2つ生成されているのがわかります。これは、出力チャネルの数を2に設定したためです。このようにして、3D畳み込みを通じて特徴量(チャネル)を増やすことが可能です。驚きですね!この結果が正しいかどうかは、皆さんが直接確認してください。要素ごとの積とバイアスを加えれば確認できます。
例題3
3つ目の例では、入力チャンネルが2、出力チャンネルが1の状況を考えます。入力テンソルは 4 × 4 × 4、フィルターは 2 × 2 × 2 のサイズに設定します。これを図で表すと以下のようになります。入力チャンネルが2つというのは、4 × 4 × 4 のサイズの入力テンソルが4次元空間にもう1つ追加されている概念です。そのため、以下の図では2つの入力テンソルが表示されています。
ただし、フィルターの数が2つに見えますが、実際にはフィルターは1つです。「フィルターが2つあるように見えるのはなぜか」と疑問に思うかもしれませんが、「Rule Four」によると、カーネルのチャンネル数は入力チャンネル数と同じです。つまり、2 × 2 × 2 のサイズのフィルターが4次元空間で1つ追加されていると考えることができます。
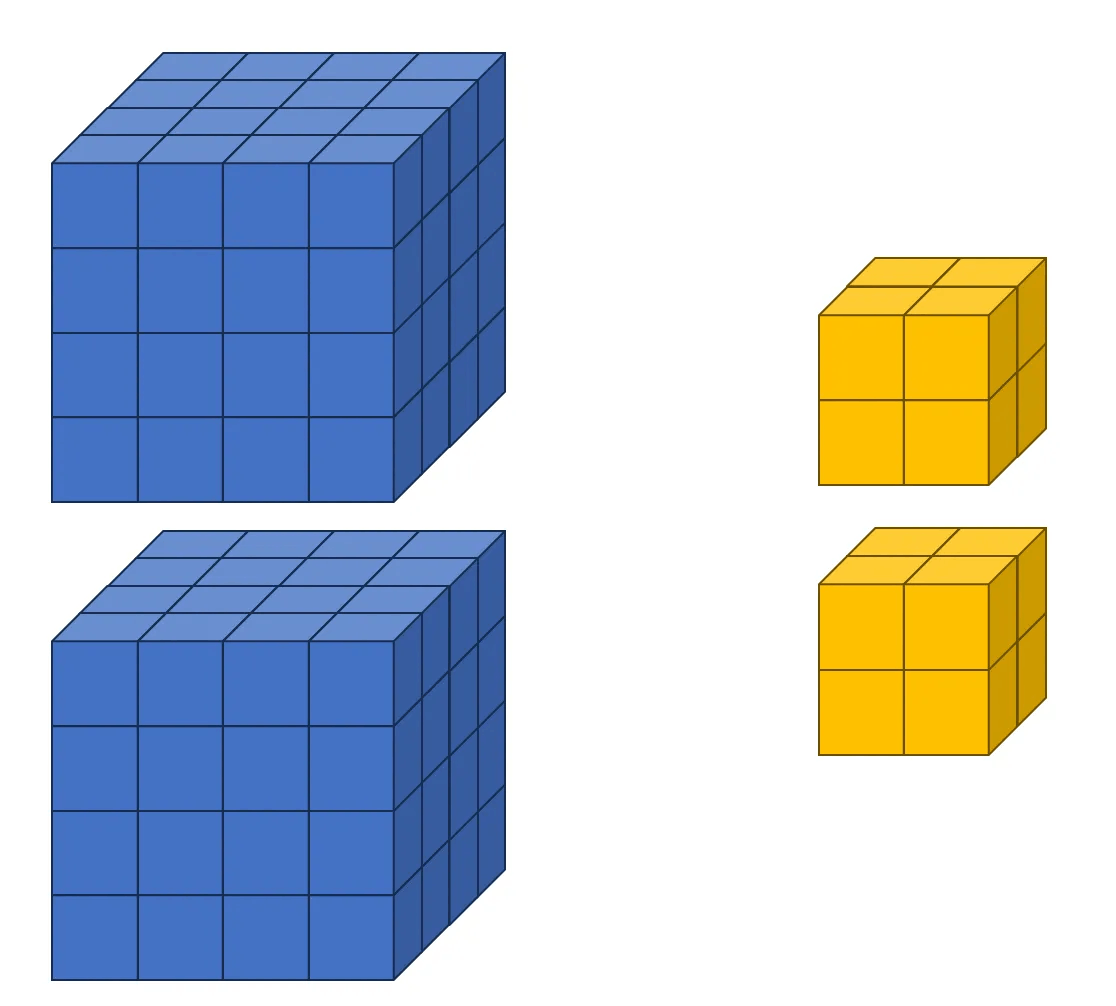
では、コードの実装に入りましょう。チャンネルが2の 4 × 4 × 4 サイズの入力テンソル tensor2 を作成します。
tensor2 = torch.randint(0, 3, (1, 2, 4, 4, 4))
tensor2 = tensor2.float()
print(tensor2.shape)
print(tensor2)
以下は出力結果です。
torch.Size([1, 2, 4, 4, 4])
tensor([[[[[1., 1., 2., 1.],
[1., 0., 0., 0.],
[0., 1., 1., 0.],
[2., 0., 1., 0.]],
[[1., 0., 1., 0.],
[0., 2., 2., 2.],
[0., 0., 1., 0.],
[0., 0., 2., 0.]],
[[0., 1., 1., 0.],
[2., 2., 0., 1.],
[1., 2., 0., 2.],
[2., 1., 0., 2.]],
[[2., 2., 1., 1.],
[1., 1., 2., 0.],
[2., 1., 0., 2.],
[1., 0., 2., 2.]]],
[[[0., 0., 1., 1.],
[1., 2., 0., 2.],
[2., 2., 2., 1.],
[0., 0., 0., 2.]],
[[0., 2., 0., 2.],
[2., 0., 2., 2.],
[2., 1., 1., 0.],
[2., 1., 1., 0.]],
[[1., 2., 0., 1.],
[0., 1., 0., 1.],
[1., 0., 2., 1.],
[0., 2., 1., 0.]],
[[2., 2., 2., 2.],
[2., 1., 0., 1.],
[0., 2., 2., 2.],
[0., 1., 1., 2.]]]]])
では、畳み込み層を定義しましょう。
conv3 = torch.nn.Conv3d(in_channels=2, out_channels=1, kernel_size=2, stride=1, padding=0)
print(conv3.weight)
print(conv3.bias)
以下は出力結果です。
Parameter containing:
tensor([[[[[ 0.0133, 0.2342],
[ 0.1972, 0.2209]],
[[-0.1670, 0.0172],
[ 0.1740, -0.2308]]],
[[[-0.0897, -0.0589],
[-0.0932, -0.1892]],
[[ 0.0225, -0.2232],
[ 0.2248, 0.1964]]]]], requires_grad=True)
Parameter containing:
tensor([-0.1614], requires_grad=True)
畳み込み演算を実行します。
F3 = conv3(tensor2)
print(F3)
以下は実行結果です。
tensor([[[[[-0.8137, 0.4164, -0.3123],
[ 0.0259, -1.0430, -0.7598],
[ 0.6380, -0.2140, -0.1393]],
[[-0.3345, 0.8193, -0.4192],
[-0.8335, 0.5835, 0.1189],
[-0.3753, 0.1232, -0.3170]],
[[ 0.4006, -0.5729, -0.1822],
[ 1.0025, 0.6979, -0.0964],
[ 0.0748, -1.0398, 0.5544]]]]], grad_fn=<ConvolutionBackward0>)
結果を見ると、チャンネルが1で 3 × 3 × 3 のサイズの出力テンソルが生成されていることが分かります。具体的には、F3[0][0][0][0][0] = -0.8137 という値が出力されています。この演算がどのように行われたのか詳しく説明します。

図で示すように、青が入力テンソル、黄色がフィルター、赤が出力結果を表しています。赤い出力結果は以下のように計算されます。
-0.8137 = 茶色領域の結果 + ピンク色領域の結果 + バイアス
Excelで計算した結果を以下に示します。
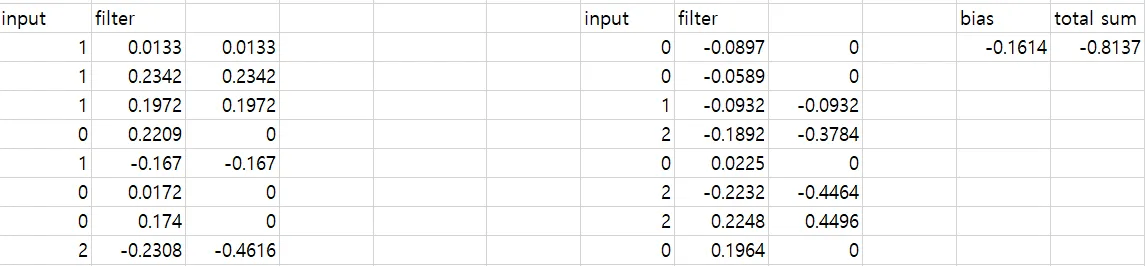
-0.8137 が正しく計算されていることが確認できます。他の領域についても確認してみてください。

エクセルで計算してみました。
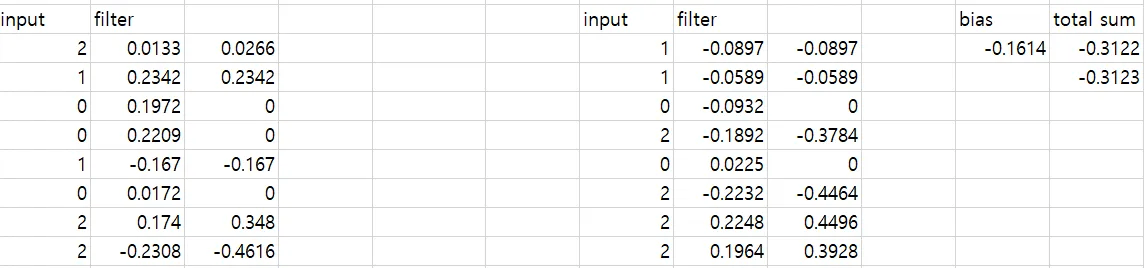
エクセル実行結果、-0.3122 が出ます。 今回も0.0001の差が存在します。 とにかく、正しく写るのが確認できます。
例題4
最後の例は、入力チャンネルが2、出力チャンネルが2の状況です。入力テンソルは 4 × 4 × 4、フィルターは 2 × 2 × 2 のサイズに設定します。これを図で表すと以下のようになります。今回は出力チャンネルが2なので、フィルターが2つ必要です。緑色がフィルター1、黄色がフィルター2を表します。また、入力チャンネルが2であるため、フィルターのチャンネル数も2になります。このため、2つのフィルターが存在し、それぞれのカーネルがチャンネル2を持つ状況です。
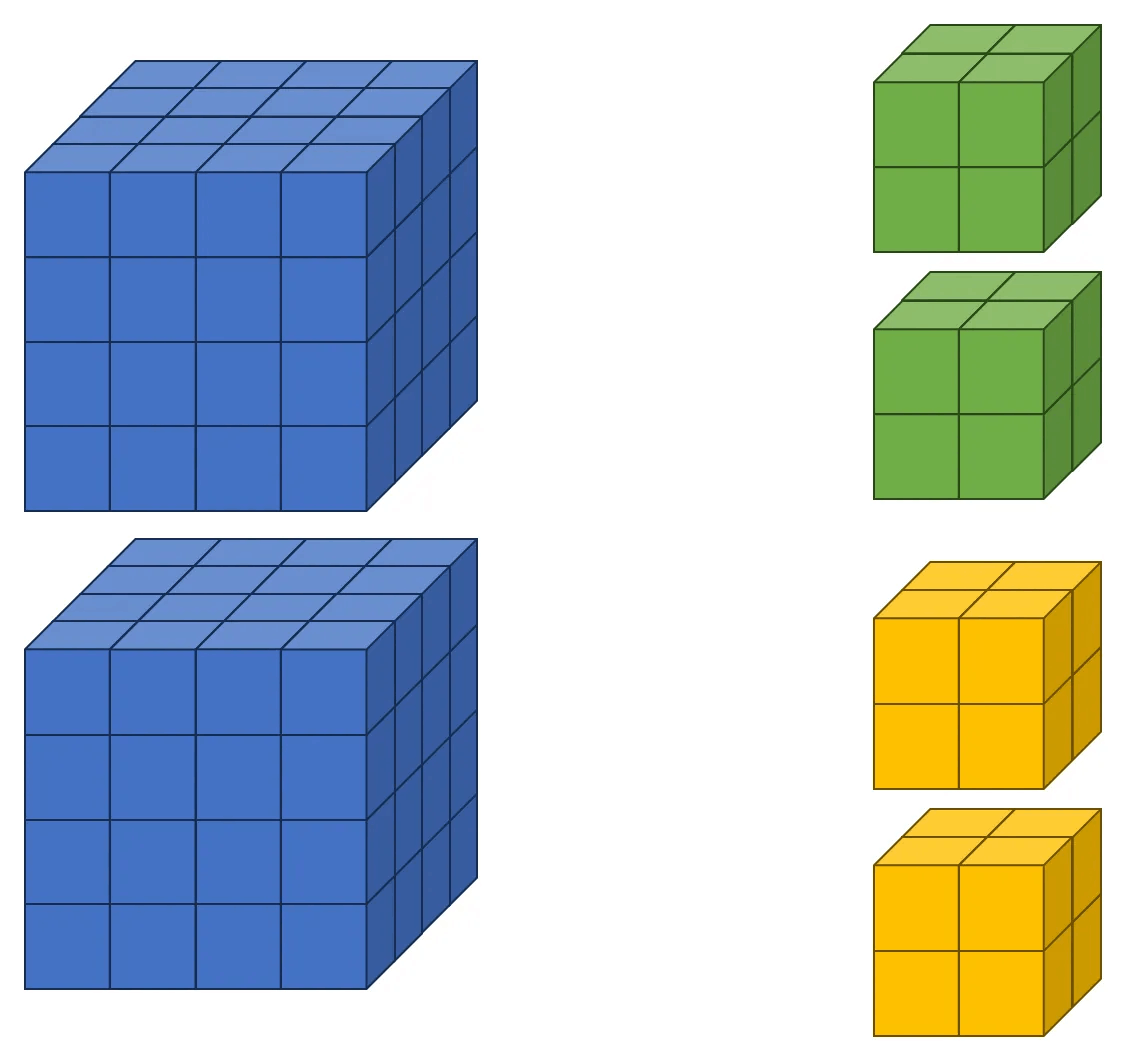
この例では、例3で使用した tensor2 を入力テンソルとして使用します。次に、入力チャンネルと出力チャンネルが両方とも2の3D畳み込み層を定義します。今回はフィルター1とフィルター2を個別に出力してみます。
conv4 = torch.nn.Conv3d(in_channels=2, out_channels=2, kernel_size=2, stride=1, padding=0)
print(conv4.weight[0])
print(conv4.bias[0])
print(conv4.weight[1])
print(conv4.bias[1])
以下は出力結果です。2つのフィルターがあり、それぞれのフィルターが2つのチャンネルで構成されていることが確認できます。
tensor([[[[ 0.1769, 0.1303],
[ 0.1416, 0.1474]],
[[-0.1709, 0.1761],
[ 0.0190, -0.0094]]],
[[[-0.2183, -0.1055],
[-0.1105, 0.1973]],
[[ 0.1401, -0.1617],
[ 0.0251, 0.0699]]]], grad_fn=<SelectBackward0>)
tensor(-0.2334, grad_fn=<SelectBackward0>)
tensor([[[[-0.1787, -0.0015],
[ 0.2239, 0.0319]],
[[-0.1900, -0.1118],
[-0.0906, -0.1865]]],
[[[ 0.1335, 0.2468],
[-0.0078, 0.2383]],
[[ 0.1911, -0.0315],
[ 0.2227, 0.2001]]]], grad_fn=<SelectBackward0>)
tensor(0.2421, grad_fn=<SelectBackward0>)
次に、畳み込み演算を実行します。
F4 = conv4(tensor2)
print(F4)
以下は実行結果です。チャンネルが2で、サイズが 3 × 3 × 3 のテンソルが生成されます。
tensor([[[[[ 0.0366, 0.4928, 0.0365],
[ 0.5875, -0.4348, -0.3152],
[-0.2290, -0.1959, -0.0302]],
[[-0.1118, 0.7814, 0.2120],
[-0.5592, 0.3803, -0.1200],
[-0.3095, -0.5714, 0.3748]],
[[ 0.3398, -0.3738, 0.2527],
[ 0.8935, 1.1104, -0.2699],
[ 0.4110, -0.1107, 0.1625]]],
[[[ 0.5739, 0.4080, 0.7786],
[ 1.9875, 0.7956, 1.0301],
[ 2.4456, 0.9522, 1.3204]],
[[ 0.2676, 1.6179, 1.3218],
[-0.1474, 0.6679, 0.9877],
[ 0.7886, 1.0273, 0.6137]],
[[ 1.7019, 0.3555, 0.6169],
[ 0.4900, 1.4752, 0.8351],
[ 0.7050, 1.0040, 0.9734]]]]], grad_fn=<ConvolutionBackward0>)
ここで、F4[0][0][1][1][1] = 0.3803 がどのようにして計算されるかを詳しく見てみましょう。

出力テンソルのチャンネル1の結果は、入力テンソルとカーネル1との畳み込み演算によって計算されます。したがって、オレンジ色のボックス内のカーネル1だけに注目すればよいです。この値 0.3803 は以下のように計算されます。
0.3803 = 緑の領域の結果 + 茶色の領域の結果 + バイアス
バイアスは -0.2334 です。これをExcelで計算すると以下のようになります。

正しい結果が得られることが確認できました!
出典
PyTorch CONV3D, https://pytorch.org/docs/stable/generated/torch.nn.Conv3d.html
A 3DCNN-LSTM Hybrid Framework for sEMG-Based Noises Recognition in Exercise, Min-Wen Lin et al., September–2020
Discussion