PointNet: 論文レビュー

最近よくnlpに関する文ばか書きましたが、久しぶりにcvに関する文を書いてみます。

Point Net開発の背景及び紹介

• Point Cloudとは、3次元空間に広がっている点の集合を意味します。 一つの点はx、y、zの値で表現できます。
• Point Cloudは不規則な特性を持っています。 不規則な特性とは、点の密集度が均一ではないことを意味します。 下の図の左側はPoint Cloudで表現したウサギ、右側はVoxelで表現したウサギです。 Voxelはマインクラフトに似た概念だと思うとわかりやすいです。
  
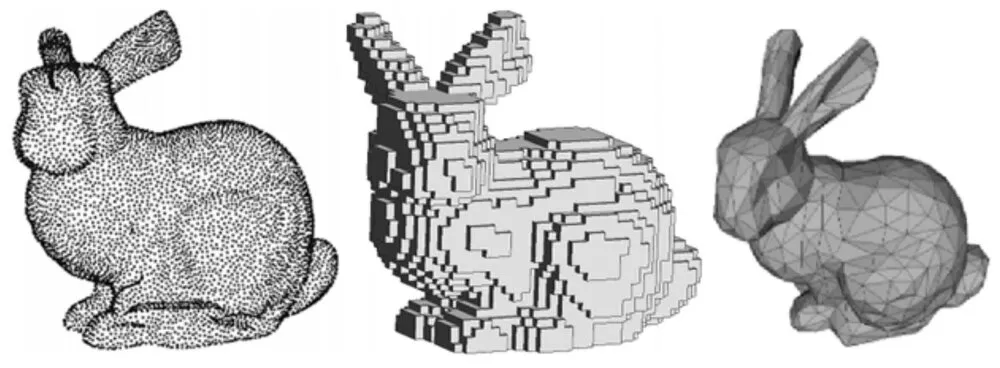
• Point Cloudの不規則な特性のため、ほとんどの研究ではPoint Cloudを3D Voxelまたは2Dイメージに変換して使用します。
• しかし、3D Voxelに変換すると、Voxel Gridの中に空きスペースがたくさんできて非効率です。 下の図を見ると、ウサギ1匹をVoxelで表現するために3次元行列を使用します。 でも、ほとんどのスペースは空いているので、スペースの無駄がひどいという問題があります。
  
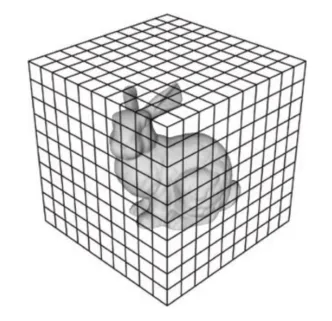
• 変換プロセスには別の問題があります。 Point CloudからVoxelに変化する過程で情報が失われます。 これはPoint CloudがVoxelに比べてウサギの姿をより具体的に表しているからです。 これはまるでアナログ情報がデジタル情報に変換されて生じるデータの消失と似ていると見れば理解しやすいです。
  
• このような問題があるので、論文の著者たちはPointNetを開発することになりました。 PointNetは、Point Cloudをそのまま入力するネットワークです。
• しかし、Point Cloudは3次元座標空間にある点が集合なので、PointNetが解決しなければならない問題があります。
• 最初の問題は、N個の点の入力順序に関係なく、常に同じ結果を出力しなければならないという点です。
• 2 番目の問題は、オブジェクトの位置が変わったり、オブジェクトが回転したりしても同じ結果を出力する必要があることです。 下の図を見れば理解しやすいと思います。 下の図は剛体運動という概念です。 剛体運動とは、並進運動(平行移動)と回転運動だけで発生する変換を意味します。
  
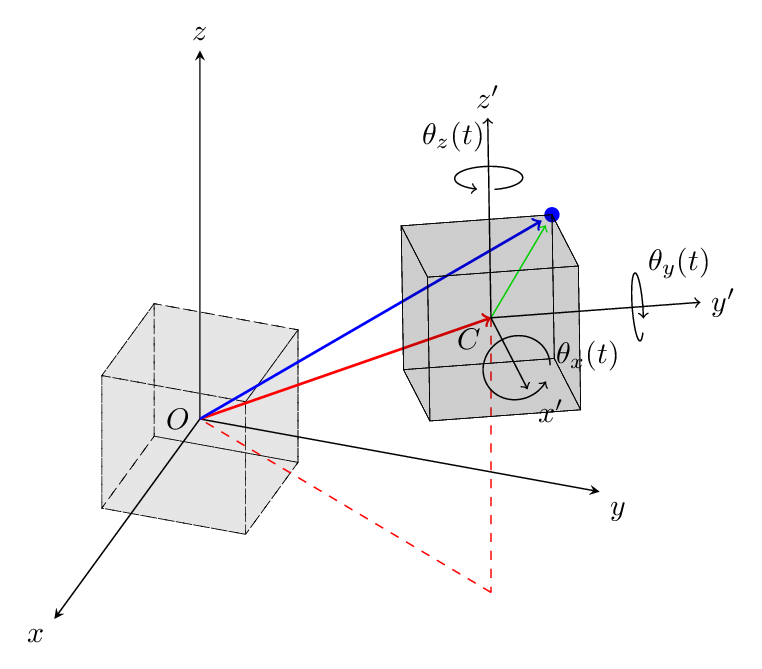
• これまでPointNetが解決しなければならない2つの問題を紹介しましたが、解決する方法は後で紹介されます。
• このような問題をすべて解決したPointNetは、Object Classification、Part Segmentation、そしてSemantic Segmentation作業を遂行できる一つの統合されたネットワーク構造で構成されています。
  

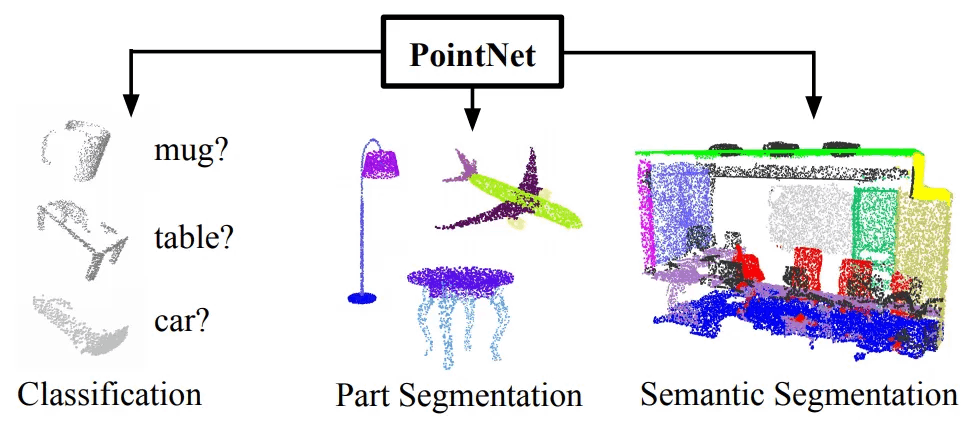
関連研究

Point Cloud Features

• ここで、Point Cloud Featuresとは、Point Cloudから抽出した特徴を意味します。 2D Object ClassificationでイメージからFeature Mapを抽出する概念と似ています。
• Point Featureは、実行しようとする作業によって開発者が望む方法で抽出することができます。 例えば、Point Featureは一点の統計的な特徴を表現することができます。
• ですから、FeatureはIntrinsicまたはExtrinsicに分類でき、時によってはLocalまたはGlobalに分類することができます。 Local Featureは一つのオブジェクトのClassification作業をする時に使用されるなら、Global FeatureはSemantic Segmentationをする時に使用できます。

Deep Learning on 3D Data

• Volumetric CNns: VoxelにCovolutional Neural Networkを適用した方法です。 しかし、Voxel Gridによって解像度に制限があります。 また、コンピュータの計算量が大きすぎるという問題があります。
• Multiview CNNs:3D Point Cloudを2Dイメージにレンダリングし、Convolutional Neural Networkを適用した方法です。 性能の良い方法ですが、3D Semantic Segmentationなどの3D作業ができないという欠点があります。 そしてレンダリング過程でコンピュータ計算量が大きいでしょう。
• Spectral CNNs: MeshにSpectral CNを適用する方法です。 Spectral CNNが何なのかよく分からないので、短所に関する説明は省略します。😅
• Feature-based DNNs:3Dデータから図形Featureを抽出する方式です。 しかし、Featureが弱いという短所があります。

Deep Learning on Unordered Sets

• Point Cloudは順序のないベクトルの集合と言えます。
• NLPはUnordered Setという言語というデータにDeep Learningを適用する分野です。
• しかし、3Dデータのように幾何学的な構造を持つ資料構造にDeep Learningを適用した事例は多くありません。

PointNetが解決しようとする問題

• PointNetは、順序が定義されていないPoint Cloud集合を入力してもらう必要があります。
• Classification作業をするためには、分類しようとするオブジェクトのPoint Cloudだけを入力値として入れる必要があります。 結果としてはk個の点数を出力できなければなりません。 この時、kは予測可能なクラスの数です。
• Part Region Segmentation作業をするためには、オブジェクトのPoint Cloud集合だけが入力値として受け取ります。 そしてnxmの点数を出力します。 この時、nはPointの個数を意味し、mは予測可能なクラスの個数です。
• Object Region Segmentaion作業をするためには、3D Sceneの部分集合を入力値として受け取ります。 そしてPart Region Segmentationと同じようにnxmの点数を出力します。

ディープラーニングを活用した解決策

PointNetが持つべき特性

PointNetに入力されるデータは、ユークリッド空間で表現される点の集合です。 下の図は、ユークリッド空間にある一点を視覚化した内容です。 単純に3D空間だと理解すれば簡単です。

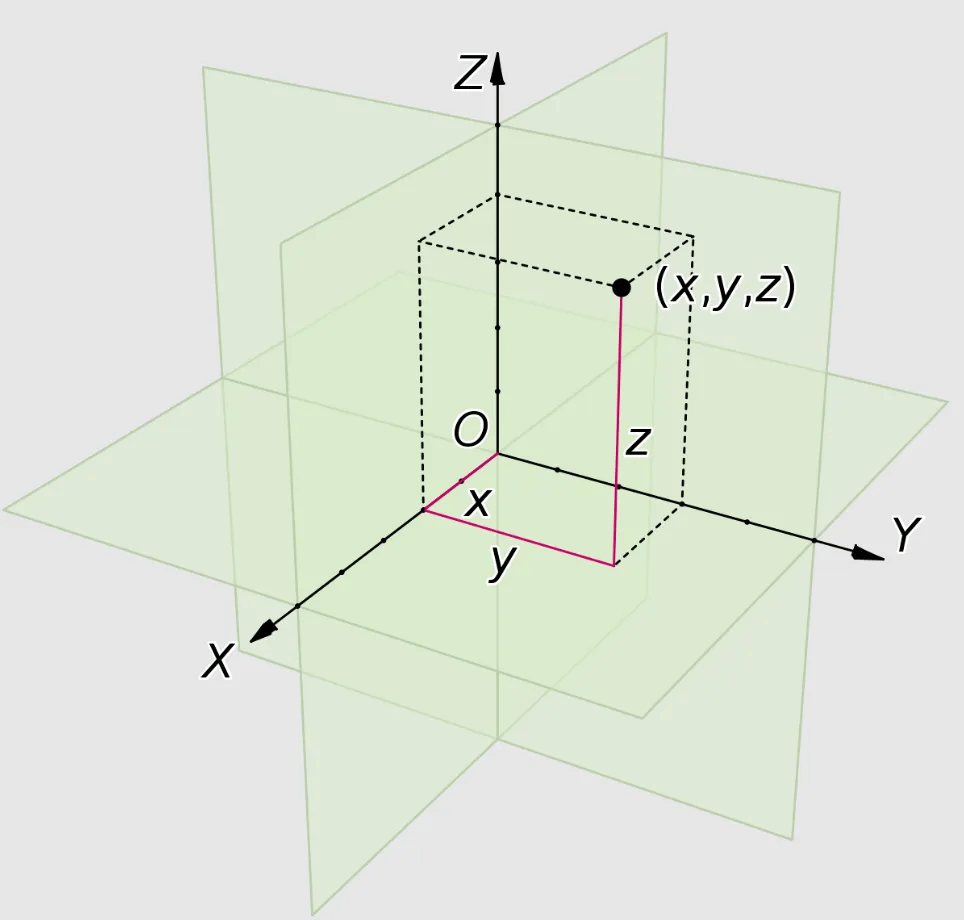
PointNetは全部で3つの特性を持っていなければなりません。 順番にご紹介します。

• Unordered Input Invariance:Point Coloudセットに含まれている点は、順序がありません。 PointNetに入力されるデータがN個なら、ネットワークはデータセットが入る順序であるN!個の順列に対して常に同じ結果を出力しなければなりません。
  
• Interaction Among Points: PointNetは近接した点の間の距離を計算し、Local Structureを理解できなければなりません。 また、Local Structure間の結合も理解できなければなりません。 たとえば、複数の丸を検出したからといって、丸を出力して終わってはいけません。 複数の丸が四角い板の上にあるのを見て、碁盤という結果を出力できなければなりません。
• Invariance Under Transformation:オブジェクトが回転または移動しても、常に同じ結果を出力する必要があります。

PointNetの構造

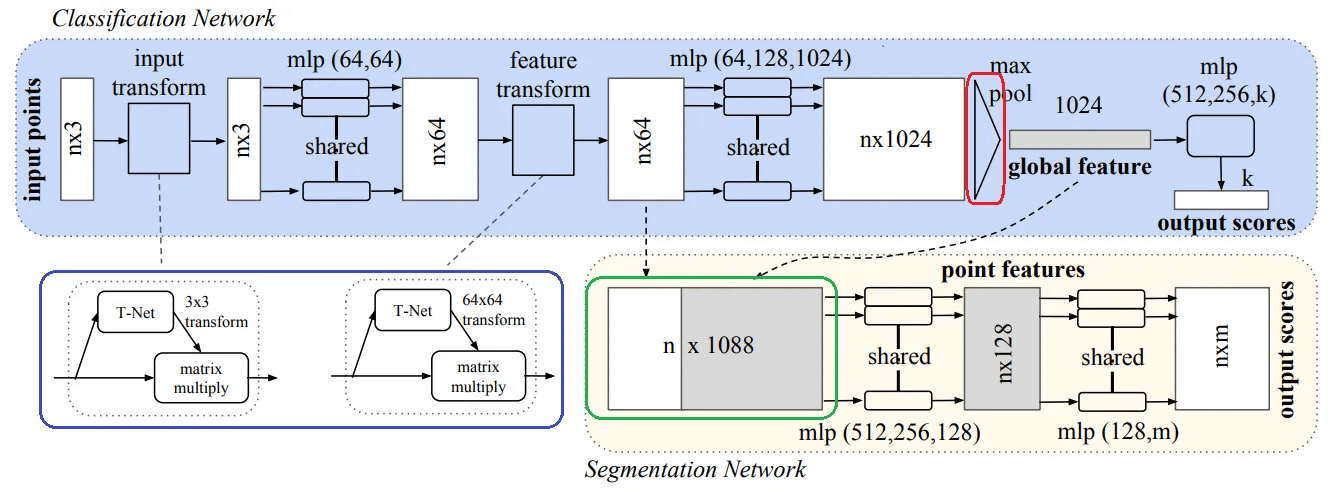
上に見える図はPointNetの構造です。 重要なモジュールは3つあります。

• Max Pooling Layer(赤色):入力されたN個の点から重要な情報を抽出します。
• Local and Global Information Combiner (グリーン):Local FeatureとGlobal Featureを統合します。
• Two Joint Alignment Networks (青):入力されたPoint Cloudと抽出されたFeatureを標準化するモジュールだと考えてください。

各モジュールについて詳しく説明します。

Symmetry Function for Unordered Input

• 上の図で赤色で打った部分です。 入力値の順序に関係のないモデルを作成するには、合計3つの方法があります。
• 最初の方法はN個のデータを整列する方式です。 しかし、N個のデータに順序というものを定義するのは難しいので、不可能に近い方式です。
• 二つ目の方法はRNNを使う方法です。 RNNの場合は、短い入力順序に対しては堅牢であることを示します。 しかし、Point Cloudのような膨大な量のデータについては学習に限界があります。
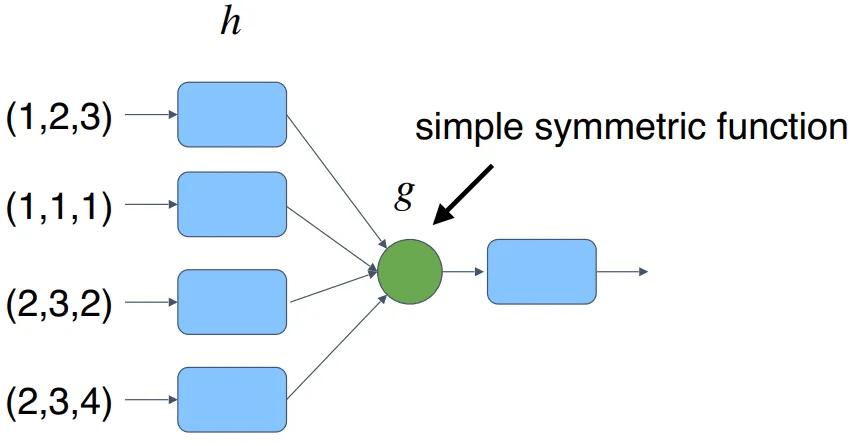
• 3 番目の方法は、簡単な対称関数を使用する方法です。 対称関数は、N個のベクトルを入力されたとき、N個のベクトルの入力順序に関係なく、常に同じ結果を出力します。 このとき対称関数とは、定義域の順序を変えても同じ結果を得る関数を意味します。 以下は対称関数の例です。
  
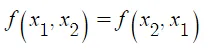
• PointNetの全体ネットワークはN個の点に対して何らかの結果を出力しなければなりません。 例えば、PointNetが行う作業がObject Classificationであれば、一つのクラスを予測する必要があります。 f(x1, x2, ···. , xn)をPointNetが予測する値とします。 この時、f(x1、x2、···. , xn)をFully Connected Layerと(以下FC)Max Poolingだけを使って素敵にするのがSummetry Function for Unordered Inputのアイデアです。 以下の式をご覧ください。
  
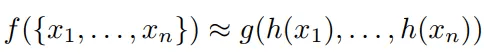
• hをFC、gをMax Poolingとします。 この時、Max Poolingは対称関数になることができます。 1、2、3をどのような順序で入れても、常に3という値が出力されるからです。 簡単に説明すると、N個のデータはFCを経てMax Poolingをするようになり、常に同じ値を持つようになるのです。 下の絵を見れば理解しやすいと思います。
  

Local and Global Information Aggregation

• PointNetがObject Classification作業だけするなら、4.2.1で得たGlobal Featureさえあればいいです。 しかし、Segmentation作業をするためには、Local FeatureとGlobal Featureに関する情報をすべて知っておく必要があります。
  
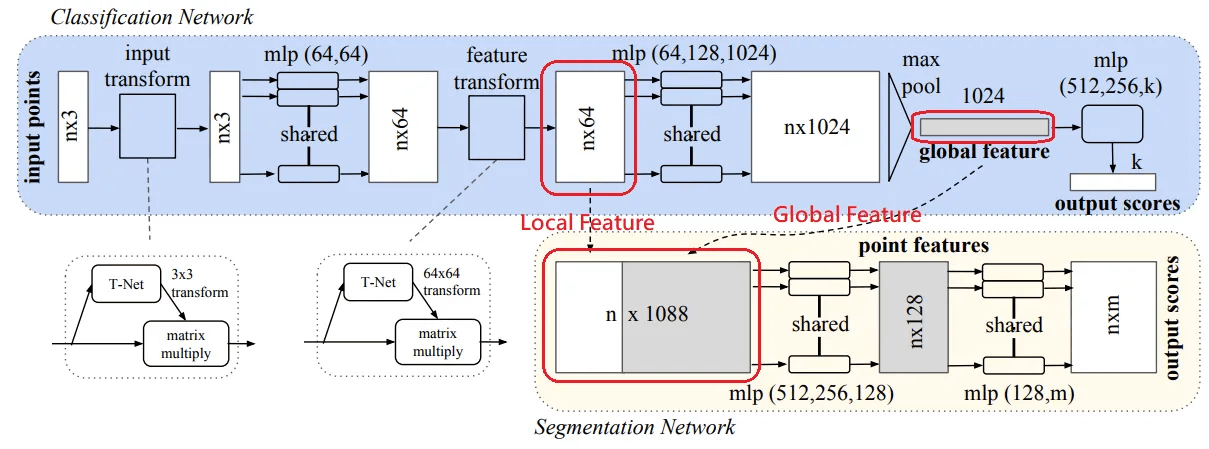
• Global Feature の計算が終わると、Local Feature の後にGlobal Feature ベクトルをつなぐことで、Global とLocal Feature を統合しました。 統合したnx1088サイズの新しいベクトルがFCを経ながら新しいPoint Feautreを持つnx128サイズのベクトルが生成されます。 この時、新しく作られたPoint FeatureはGlobalとLocalの情報を含んでいます。

Joint Alignment Network

• 上の図で赤色で表示した部分に対する説明です。 Point Cloudが剛体運動をして、オリジナルのPoint Cloudと違っても、PointNetは常に同じ結果を出力できる必要があります。 そのために使用された簡単なネットワークがJoint Alignment Networkです。
• まず、赤いボックスの中の左側の絵を見てください。 アイデアは簡単です。 T-Netを経て、すべての点が標準化された空間に置かれるようにすることが目的です。 つまり、T-Netが3x3サイズのアフィン変換行列を(Affine Transformation Matrix)よく予測できるようにすればいいのです。 n x 3 サイズの入力データは、3 x 3 サイズのアフィン変換行列と乗算して標準化されます。
• 赤いボックスの中の右側の絵を見てください。 ここで使用されるT-Netも同様の方法で使用されます。 Input Transformation を経てから出力された nx3 サイズのベクトルは、FC を経てFeature が抽出されます。 この時に出力された結果はnx64サイズですが、Feautre空間に対しても標準化作業を経るために2番目のT-Netが使用されます。 この時、T-NetはFeature変換行列を(Feature Transformation Matrix)予測します。 2 番目のT-Netは、64 x 64 サイズの行列を予測します。 これは、最初のT-Netが予測した3x3よりもはるかに大きいため、学習が困難です。 そこで、PointNetのSoftmax Lossに以下のRegularization項を追加します。
  
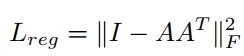
• Aは2番目のT-Netが予測する64x64サイズの行列です。 この時、Aは直交行列になるように制約を受けます。 直交行列は入力時に情報消失がないそうですが、どういうことかよくわかりません。 ご理解いただけましたら、コメントお願いします！ とにかくRegularization項を追加するので、学習がより安定的で、PointNetの性能が上がりました。

code

分類ネットワーク

def get_model(point_cloud, is_training, bn_decay=None):
    """ Classification PointNet, input is BxNx3, output Bx40 """
    batch_size = point_cloud.get_shape()[0].value
    num_point = point_cloud.get_shape()[1].value
    end_points = {}
    with tf.variable_scope('transform_net1') as sc:
        transform = input_transform_net(point_cloud, is_training, bn_decay, K=3)
    point_cloud_transformed = tf.matmul(point_cloud, transform)
    input_image = tf.expand_dims(point_cloud_transformed, -1)
    net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv1', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 64, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv2', bn_decay=bn_decay)
    with tf.variable_scope('transform_net2') as sc:
        transform = feature_transform_net(net, is_training, bn_decay, K=64)
    end_points['transform'] = transform
    net_transformed = tf.matmul(tf.squeeze(net, axis=[2]), transform)
    net_transformed = tf.expand_dims(net_transformed, [2])
    net = tf_util.conv2d(net_transformed, 64, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv3', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 128, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv4', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 1024, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv5', bn_decay=bn_decay)
    # Symmetric function: max pooling
    net = tf_util.max_pool2d(net, [num_point,1],
                             padding='VALID', scope='maxpool')
    net = tf.reshape(net, [batch_size, -1])
    net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
                                  scope='fc1', bn_decay=bn_decay)
    net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
                          scope='dp1')
    net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
                                  scope='fc2', bn_decay=bn_decay)
    net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
                          scope='dp2')
    net = tf_util.fully_connected(net, 40, activation_fn=None, scope='fc3')
    return net, end_points

MLPの中核的なアプローチ:

input_image = tf.expand_dims(point_cloud_transformed, -1)
net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv1', bn_decay=bn_decay)
net = tf_util.conv2d(net, 64, [1,1],
                     padding='VALID', stride=[1,1],
                     bn=True, is_training=is_training,
                     scope='conv2', bn_decay=bn_decay)

conv2d:

def conv2d(inputs,
           num_output_channels,
           kernel_size,
           scope,
           stride=[1, 1],
           padding='SAME',
           use_xavier=True,
           stddev=1e-3,
           weight_decay=0.0,
           activation_fn=tf.nn.relu,
           bn=False,
           bn_decay=None,
           is_training=None):
  """ 2D convolution with non-linear operation.
  Args:
    inputs: 4-D tensor variable BxHxWxC
    num_output_channels: int
    kernel_size: a list of 2 ints
    scope: string
    stride: a list of 2 ints
    padding: 'SAME' or 'VALID'
    use_xavier: bool, use xavier_initializer if true
    stddev: float, stddev for truncated_normal init
    weight_decay: float
    activation_fn: function
    bn: bool, whether to use batch norm
    bn_decay: float or float tensor variable in [0,1]
    is_training: bool Tensor variable
  Returns:
    Variable tensor
  """
  with tf.variable_scope(scope) as sc:
      kernel_h, kernel_w = kernel_size
      num_in_channels = inputs.get_shape()[-1].value
      kernel_shape = [kernel_h, kernel_w,
                      num_in_channels, num_output_channels]
      kernel = _variable_with_weight_decay('weights',
                                           shape=kernel_shape,
                                           use_xavier=use_xavier,
                                           stddev=stddev,
                                           wd=weight_decay)
      stride_h, stride_w = stride
      outputs = tf.nn.conv2d(inputs, kernel,
                             [1, stride_h, stride_w, 1],
                             padding=padding)
      biases = _variable_on_cpu('biases', [num_output_channels],
                                tf.constant_initializer(0.0))
      outputs = tf.nn.bias_add(outputs, biases)
      if bn:
        outputs = batch_norm_for_conv2d(outputs, is_training,
                                        bn_decay=bn_decay, scope='bn')
      if activation_fn is not None:
        outputs = activation_fn(outputs)
      return outputs

alignment network

def input_transform_net(point_cloud, is_training, bn_decay=None, K=3):
    """ Input (XYZ) Transform Net, input is BxNx3 gray image
        Return:
            Transformation matrix of size 3xK """
    batch_size = point_cloud.get_shape()[0].value
    num_point = point_cloud.get_shape()[1].value
    input_image = tf.expand_dims(point_cloud, -1)
    net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv1', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 128, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv2', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 1024, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv3', bn_decay=bn_decay)
    net = tf_util.max_pool2d(net, [num_point,1],
                             padding='VALID', scope='tmaxpool')
    net = tf.reshape(net, [batch_size, -1])
    net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
                                  scope='tfc1', bn_decay=bn_decay)
    net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
                                  scope='tfc2', bn_decay=bn_decay)
    with tf.variable_scope('transform_XYZ') as sc:
        assert(K==3)
        weights = tf.get_variable('weights', [256, 3*K],
                                  initializer=tf.constant_initializer(0.0),
                                  dtype=tf.float32)
        biases = tf.get_variable('biases', [3*K],
                                 initializer=tf.constant_initializer(0.0),
                                 dtype=tf.float32)
        biases += tf.constant([1,0,0,0,1,0,0,0,1], dtype=tf.float32)
        transform = tf.matmul(net, weights)
        transform = tf.nn.bias_add(transform, biases)
    transform = tf.reshape(transform, [batch_size, 3, K])
    return transform

lose

def get_loss(pred, label, end_points, reg_weight=0.001):
    """ pred: B*NUM_CLASSES,
        label: B, """
    loss = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=pred, labels=label)
    classify_loss = tf.reduce_mean(loss)
    tf.summary.scalar('classify loss', classify_loss)
    # Enforce the transformation as orthogonal matrix
    transform = end_points['transform'] # BxKxK
    K = transform.get_shape()[1].value
    mat_diff = tf.matmul(transform, tf.transpose(transform, perm=[0,2,1]))
    mat_diff -= tf.constant(np.eye(K), dtype=tf.float32)
    mat_diff_loss = tf.nn.l2_loss(mat_diff) 
    tf.summary.scalar('mat loss', mat_diff_loss)
    return classify_loss + mat_diff_loss * reg_weight

実験結果

各作業の実験結果

• ここは、PointNetが実行できる3D Object Classification、Object Part Segmentation、Semantic Segmentationの実験結果を説明します。
• 実験の詳細については、論文の裏側にあるSupplementary Sectionをご覧ください！

3D Object Classification

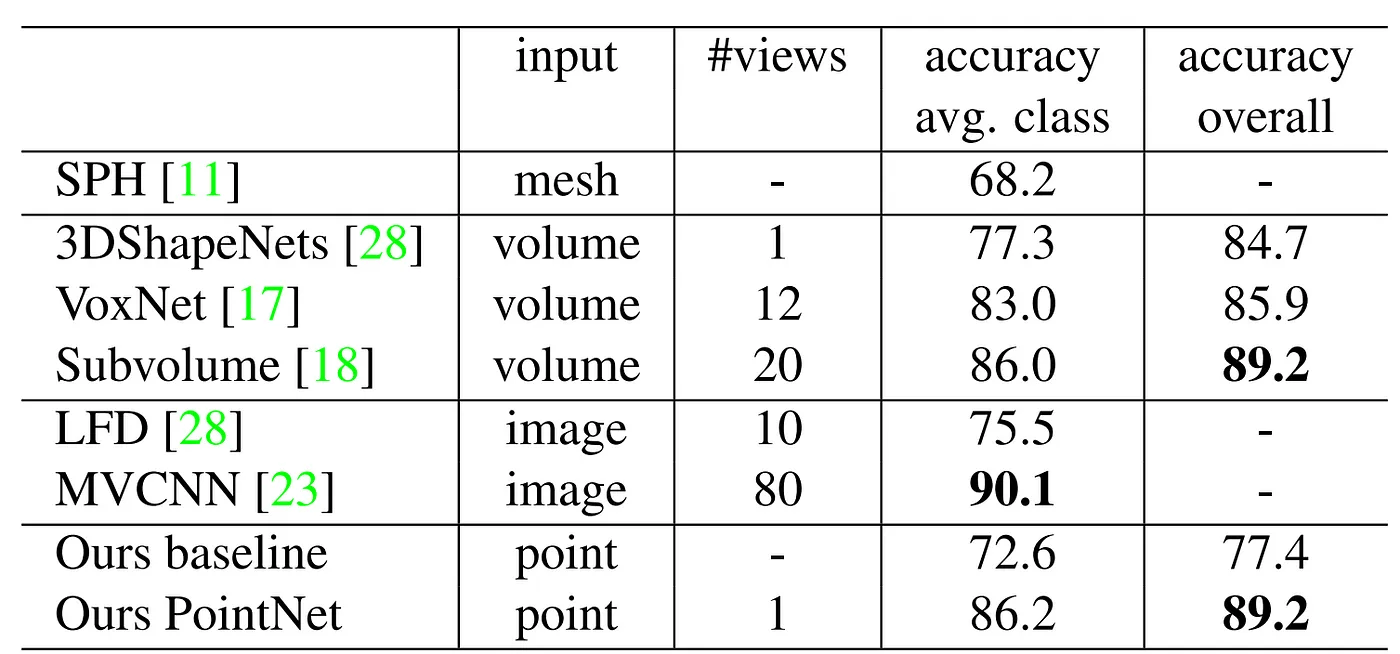
• 入力値がMesh、Voxel、ImageであるState-of-the-art 3D Object Classificationモデルと性能を比較した表です。 実験はModelNet40データセットで行われました。
• PointNetを学習するために、学習データのMesh面から1024個の点を均一にサンプリングしました。
  入力値がVoxelであるClassificationモデルと比較した時、より良い性能を見せました。
• ここで「Ours baseline」というモデルの結果も含まれていますが、どんなモデルを意味するのかわかりません。 おそらく論文のSupplementary Sectionに出るのではないかと思います。

3D Object Part Segmentation

• 上の表は、他の3D Object Part SegmentationモデルとPointNetを比較した結果です。 実験のためにShapeNetデータセットが使用されました。
• PointNetの点数が他のモデルの平均点数よりもっと高いです。 点数はIoUで計算されました。 まず、各クラスのGrud-truthと予測された部分の間にIoUを求めます。 そして、各クラスIoUの平均を求めたのが表の2列目に属する値です。

Semantic Segmentation in Scenens

• 上の表は、PointNetとBaselineモデルのSemantic Segmentationの結果を比較した表です。 比較のためにStanford 3Dデータセットを使用しました。
• 数値の違いだけ見てもわかります。 PointNetが圧倒的に性能に優れています。

Ablation Experiment

Order-invarient方式に対する比較

• 上に順序のないN個の入力値に対して、常に同じ結果が出力される3つの方法について見てきました。 以下の表は、3つの方法を比較した実験結果です。
  
• 3つの方式の中でMax Poolingが最も点数が高いです。

Inputと Feature Transformationの効果 (T-Net)

• 以下の表は、Input Transformation と Feature Transformation を実行したときの結果を示します。
  
• InputとFeature Transformationの両方を使用していない時の結果だけを見ても点数が高いです。 しかし、両方を使用した場合、89.2%の精度を示します。

PointNetの強健さ

• 一番左のグラフを見てください。 N個のPoint Cloudがある集合Sがある場合、Random Input Sampling方式で点を削除した場合の性能変化に対するグラフが赤い線です。 Sの50%になる量の点が除去された時も性能は3.8%しか落ちません。 おそらくMax Poolingを使うので、点数があまり落ちていないと思います。
• 真ん中のグラフを見てください。 Outlierについての実験です。 ここでは青い線だけ見てください。 集合Sで20%の点がOutlierであっても性能は80%以上です。 このような性能が出るのも、Max PoolingによってOutlierが無視されたからだと思います。
• 右のグラフを見てください。 集合Sにすべての点に対してGaussian Noiseを与えたときの性能評価です。 x軸は分散ですが、値が大きくなるほど性能が落ちることが確認できます。 分散が0.05の場合、性能が80%近く出ます。

結論及び感じた点

結論

• PointNetは、Point Cloudデータを前処理なしでそのまま入力できます。 Object Classification、Part Segmentation、Semantic Segmentationができるひとつになったネットワークです。 その一方で、他のState-of-the-artモデルと性能を比較すると、比較するに値するか、より優れています。

感じたこと

• 2D Object Detectoin モデルは入力サイズが決まっていました。 しかし、PointNetは入力サイズが(N個の点)制限されないという点で使いやすいと感じました。
• 順序のないPoint Cloud入力に対して、常に同じ結果を出力させる方法がまだ100%理解できません。 Symmetric FunctionとMax Poolingを使ってこれを可能にしたことが大体分かりますが、正確に理解したとは思えません。 難しいです。

出典

• PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation, Qi et al., 2017–04–10
• [3D MACHINE LEARNING] — 3D DATA REPRESENTATIONS, Antoine Toisoul, 2021–03–18
• PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation, Computer Vision Foundation, 2017–08–12