自然言語から最適化モデルへ、Autoformulationについて

物流、製造、金融などあらゆる意思決定を支える技術基盤として数理最適化はかなり強力な手法であり、ここ最近では強力かつ安価なヒューリスティックソルバーが出てきているなど、その利用がアカデミックから産業界へどんどん活用されていっています。

一方で、「定式化」という数学的なモデリングにはかなり時間を要するし、それなりに専門知識も必要になってきます。

また、基本的なモデリングを理解したとして、実際の業務フローを数式に直すとなると苦戦することになると思います。

最近では、LLMの躍進により業務上の制約を数学モデルに落とし込むための方法がそこそこ目につくようになりました。

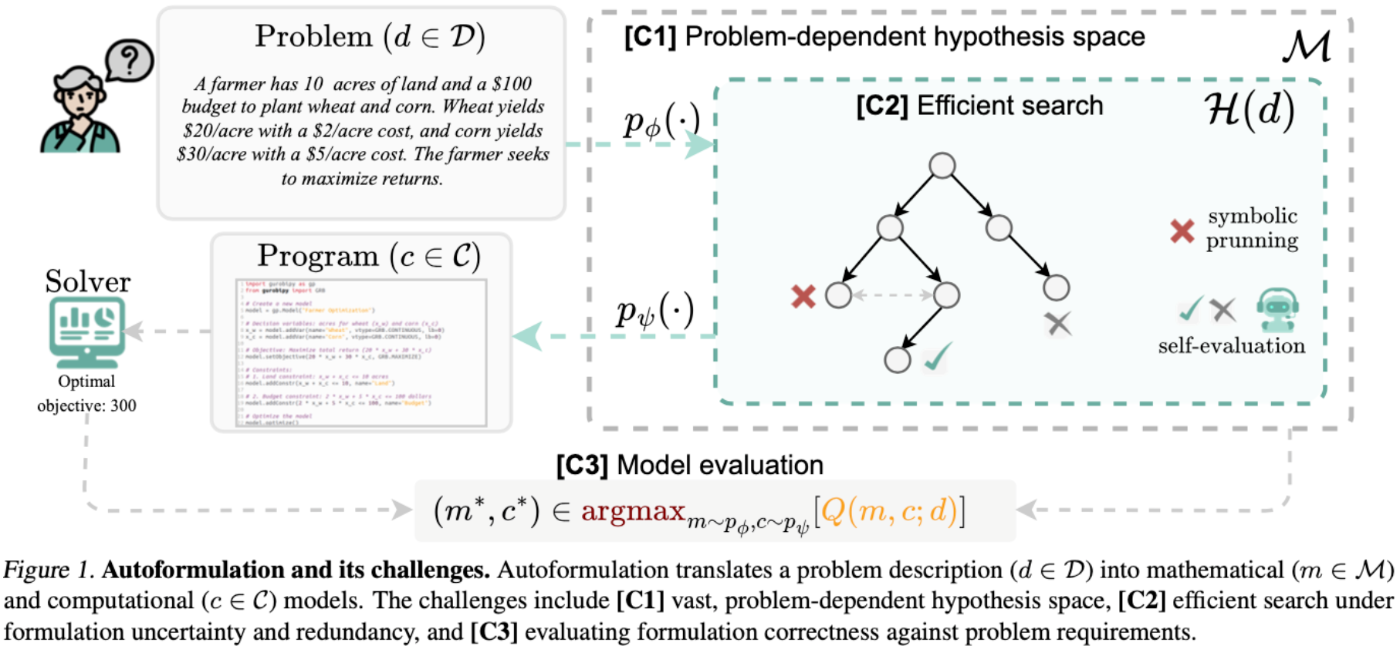
本記事ではICML 2025で発表された「Autoformulation of Mathematical Optimization Models Using LLMs」の論文で紹介されている自動定式化手法をみていきます。

概要

モデルを構築するためには、一般的にまずは業務要件を確定させ、その要件を数式として表現する必要があります。
効率的な解き方をするために、定式化をチューニングする必要があります。
どちらも専門性が必要であり、特に後者は顕著かなと思います。

こういった技術的なボトルネックを自動定式化で解消しようという試みです。

この論文では、定式化を「巨大な仮説の中から、正しい式を探す問題」として定義されています。

---

$\mathcal{D}$: 自然言語問題
$\mathcal{M}$: 定式化
$\mathcal{C}$: 計算空間
$P$: 確率空間

1. 定式化: $p_\phi: \mathcal{D} \rightarrow P(\mathcal{M})$
2. 計算表現: $p_{\psi}: \mathcal{M} \rightarrow P(\mathcal{C})$
3. 自動最適化: $p_{\phi, \psi}(m, c | d) = p_{\psi}(c | m) \cdot p_{\phi}(m | d)$
4. 目的関数: $(m^*, c^*) \in \underset{m \sim p_{\phi}, c \sim p_{\psi}}{\operatorname{argmax}} Q(m,c;d)$

$Q$については、評価基準であり、定式化が実行可能かどうかを評価する際に用いられます。

---

難しさは主に3つになります。

• 問題ごとに仮説空間が広い
• 効率のいい探索方法
• 評価方法

まず、仮説空間についての探索は、LLMを利用して変数作成、目的関数生成、等式制約、不等式制約の４段階に分解し、モンテカルロ木探索（MCTS）で順次拡張していく方針をとっています。
その後、SMTで「2x+3y=1」と「2x+3y-1=0」は同じだよね。といったような機能的に同じものを枝刈りするような形をとっています。

評価方法については後述しますが、本論文では実行可能かどうかとコードのスコアをLLMによって評価させています。

手法

近い研究として、Chain‑of‑Experts（LLMの役割分担で“完成形の式”を生成→改変）や OptiMUS（LLMとソルバーの連携）、ORLM（最適化モデリングに特化して学習された LLM）などが紹介されています。
ここでは、以下のような枠組みで定式化が進められています。

4ステップ分解 × MCTS × SMT

数式は次の4つの部品に分けて作ります

1. パラメータ、決定変数: $m_1$
2. 目的関数: $m_2$
3. 等式制約: $m_3$
4. 不等式制約: $m_4$
   各段で前段の出力を前提に LLM が複数の候補を出します。
   段階を踏んで実行するため、自動最適化:

$$\begin{align*} p_{\psi}(c | m) \cdot p_{\phi}(m | d) &= p_{\psi}(c | m) \cdot p_{\phi}(m_{1} | d) \cdot p_{\phi}(m_{2} | m_{1}, d) \cdot p_{\phi}(m_{3} | m_{1}, m_{2}, d) \cdot p_{\phi}(m_{4} | m_{1}, m_{2}, m_{3}, d) & \\ &= p_{\psi}(c | m) \cdot \prod_{i=1}^4 p_{\phi}(m_{i} | m_{<i},d)& \end{align*}$$

の形で階層化します。

ここでの各段階の生成結果を元に選択と拡張を繰り返すMCTSの戦略とSMTによる枝刈りで定式化を行なっていきます。

評価$Q$については、最終ノード$\vec{n_{t}}$をpython用のプログラムへパース($\text{parser}(\vec{n_{t}})$)してが最適解を導出するかどうか($=S$)とLLMによる評価($E_{\text{LLM}}$)を組み合わせて、$\mathbb{1}_{S}[\text{parser}(\vec{n_{t}})] \cdot E_{\text{LLM}}^{m}(\vec{n_{t}} ; d)$を評価として与えています。
実際の指示関数$\mathbb{1}_{S}$についてはモデリングによる実行可能性と最適性などとそもそもプログラムとして動くかどうかなどのチェックが入ると思います。

実際には、ヒューリスティックを利用するのか厳密解を利用するのか、線形、非線形なのかでも結構かわってきますし、容易に制約チェックができない物もあったりするかなと思います。

また、レビューでも指摘されていますが、一般化に対するロバスト性はどうなるかは気になります。
場合によっては、定式化までを目標として、モデリング自体は自分たちでやるっていう形でもいいかもしれません。

その場合は、$E_{\text{LLM}}^{m}(\vec{n_{t}} ; d)$のみを評価値として利用するのもありかなと思います。

コードにすると？

疑似コードとして書くと以下のような感じになると思います。

from litellm import acompletion # llm呼び出し
import z3 # smt

MODEL = "gpt-4"
API_KEY = "your-api-key"
problem = "<自然言語による問題記述>"

root = MCTSNode()

for simulation in range(num_simulations):
  node = root
  
  # Selection: UCT最大の子を選択
  while not node.is_terminal() and node.is_fully_expanded():
    node = max(node.children, key=lambda n: n.uct_value())
  
  # Expansion: LLMで次段階の候補を生成
  if not node.is_terminal():
    next_stage = node.stage + 1
    
    # m1生成: 変数
    # m2生成: 目的関数
    # m3生成: 等式制約 + SMT枝刈り
    # m4生成: 不等式制約 + SMT枝刈り
    # -----------------------------------
    M = conditions(next_stage) # m < next_stageに応じた条件を取得
    prmopt = prompts(next_stage) # stage: m1,m2,m3,m4ごとのプロンプトを取得
    response = await llm_generate(prompt, problem, M)
    candidates = parse_candidates(response)
    for c in candidates:
      child = create_child(node, c)
      node.children.append(child)
    node = node.children[0]
  
  # Simulation: 終端まで展開して評価
  while not node.is_terminal():
    node = await expand_random(node, problem)
  q = await evaluate(node, problem)
  
  # Backpropagation: 価値を親へ伝播
  while node is not None:
    node.visits += 1
    node.value += q
    node = node.parent

# 最良ノードを取得
best_node = get_best_terminal_node(root)

論文中では、独自パーサーを利用してコードを取得していますが、そこまで準備するのも大変かなと思うので、そこでもllmを使えば楽なんじゃないかなとも思います。
精度は落ちるかもしれませんが。

実験

• NL4OPT（LP 244題）、IndustryOR（LP/ILP/MILP 100題）、ComplexOR（実務OR 37題）、MAMO‑ComplexLP（211題）の4セットで評価。
• 指標は“最適目的値を再現できたか”の（精度）。GPT4‑0613を共通の基盤 LLMとして比較。
  

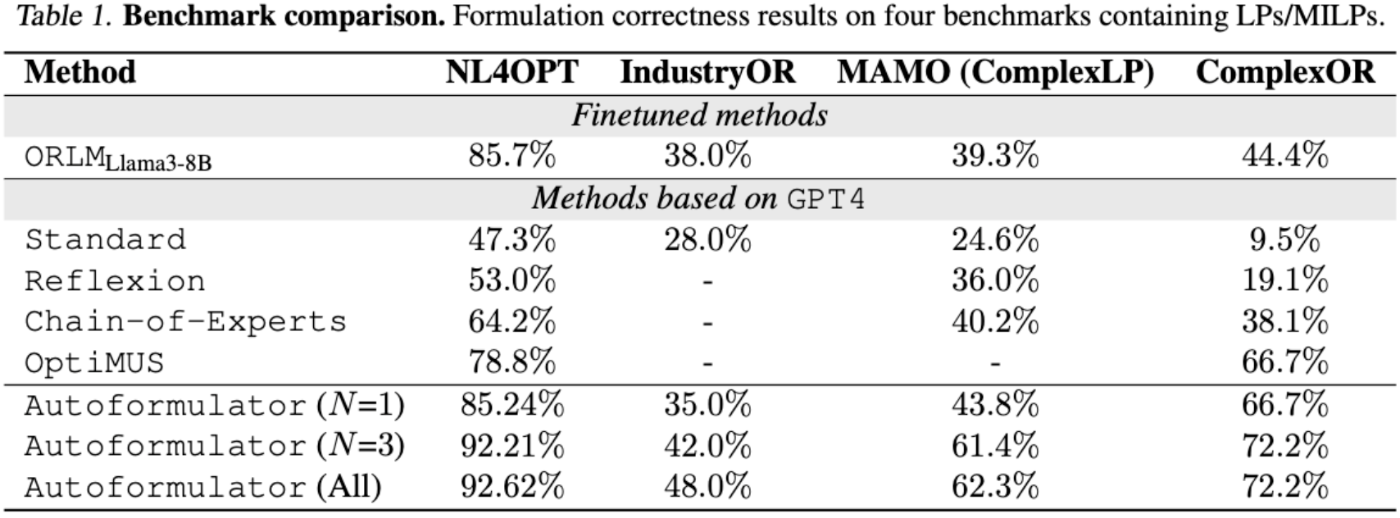
MCTSを３回のロールアウトをした段階でSOTAを達成しています。
数式を構築するプロセスとして、変数を決定する→制約を表現する→目的関数の設計→モデリングという形を取っているので、良い結果が生まれているのかもしれません。

ただ思うのは、実際にプログラムを構築していく上では、「目的関数がどうなるか？→変数を決定→制約の表現→補助変数を追加→目的関数を修正」のような段階を踏むので、$\prod_{i=1}^4 p_{\phi}(m_{i} | m_{<i},d)$のプロセスはもしかすると改善の余地があるのかもしれません。