📌

JSPのためのグラフ表現について

つかもと

2024/06/24に公開

こんにちは！Fusic 機械学習チームの塚本です。

機械学習モデルの開発から運用までなんでもしています。もし、機械学習で困っていることがあれば、気軽にお問い合わせください。

定式化をする時に、だいたいが問題をグラフで表現して、それを入力として定式化をしていくって流れをとっていきます。
今回はJSP(Job Shop Scheduling)に近いものを案件で取り扱うことがあり、論文とかはもちろんあるんですが、意外と記事とかはないんだなあって感じだったので、書いておきます。

問題設定

ジョブショップスケジューリング問題は、複数のジョブがあり、各ジョブは特定の順序で複数の機械で処理される必要がある状況を指します。各ジョブの各工程の処理時間は既知であるとし、具体的な目標は色々ですが、よくあるのは全体の完了時間（Makespan）の最小化がよくあがります。
データ設定として、例えば下のようなものがあったりします。

ジョブと機械

ジョブ： 3つ（ $J_1, J_2, J_3$ ）
機械： 3台（ $M_1, M_2, M_3$ ）

ジョブ	工程1( $O_1$ )	工程2( $O_2$ )	工程3( $O_3$ )
$J_1$	2時間	4時間	3時間
$J_2$	3時間	3時間	4時間
$J_3$	1時間	3時間	4時間

定式化のためのグラフ表現

グラフ

定式化を起こす前にまずグラフとして、オペレーション同士の関係性などを表現することでグラフ的な解析や視覚化や定式化のやりやすさが結構変わってきます。
ジョブショップでよく使われるグラフ表現はDisjunctive Graphというものがあります。
各工程間の関係性と、同一マシン内での関係性を一つのグラフで表現したものです。

[↓参考]

このグラフは、以下の要素で成り立っています。
1.　ノード

各ノードはオペレーションを表します。
ノード $(j,i)$ はジョブ $j$ の第 $i$ 番目のオペレーションを表します。

2.　Conjunctive Edges:　同一ジョブ内のオペレーションの順序を表します。

3.　Disjunctive Edges:　同一マシン上の異なるジョブのオペレーション間の順序を表します。

ソースノードとシンクノードの設定

例えば、３つのジョブにそれぞれ３つずつオペレーションが存在し、３つのマシンで処理されるものを考えると、以下のようなグラフとなります。

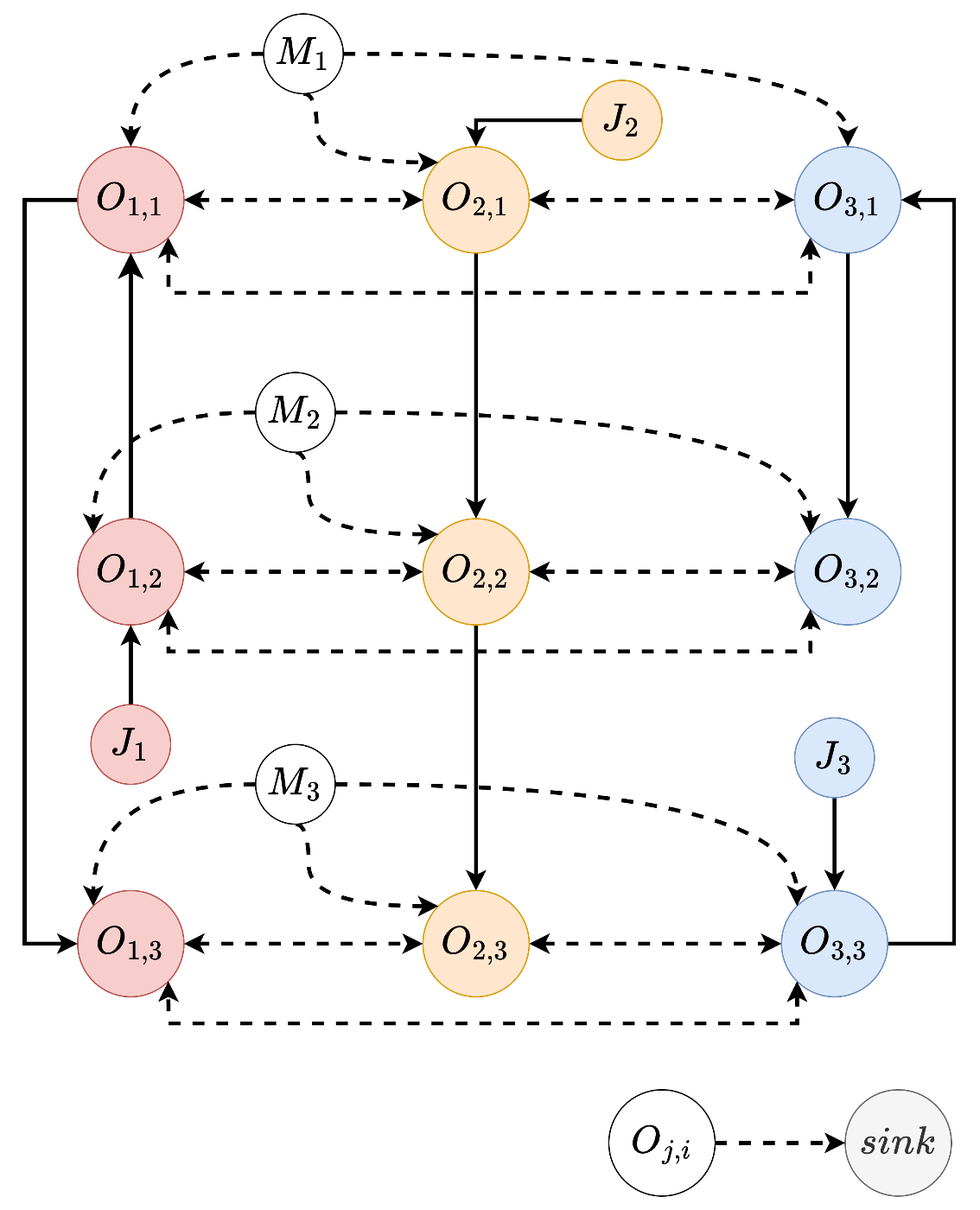
Conjunctive Edgesに繋がるソースノードとしてジョブ、Disjunctive Edgesにつながるソースノードとしてマシンを与えています。
マシン $M_1$ に処理されるオペレーションは $O_{1,2}, O_{2,1}, O_{3,2}$ というように、どのマシンでどのオペレーションを処理するのか、各オペレーションはどのジョブから派生されたものなのかを表現しています。
また、オペレーションにsinkノードを繋げています。
これを追加すれば、最終的なジョブの完了時間(makespan: $C_{\max}$ )$をsinkの開始時間として利用できます。
sinkは仮想ノードではあるので、これの開始時間みたいにすると変ですが、簡単のため今回はこうします。

定式化

各種記号定義

これから使う記号を定義しておきます。
$J$ : ジョブ集合
$O$ : オペレーション集合
$M$ : マシン集合
$O(j \in J)$ : ジョブ $j$ のオペレーション集合
$O(m \in M)$ : マシン $m$ で処理されるオペレーション集合
$N = J \cup O \cup M$
$E^c$ : Conjunctive Edges
$E^d$ : Disjunctive Edges
$E = E^c \cup E^d$
$t(n \in O)$ : オペレーション $o$ の処理時間
$\delta^{+(-)}(n \in N)$ : ノード $n$ の出（入)枝集合

定式化

ここまでのグラフを使って定式化を行います。
定式化は一般的なJSPのメイクスパンの最小化を行います。

決定変数はConjunctive EdgesとDisjunctive Edgesの枝の選択を0-1変数 $x_e (e \in E^d)$ で表し、各オペレーションの開始時間として時間変数 $s_n (n \in N)$ を使います。
$x_e=1$ となるときは、この枝 $e$ のたどる順番通りにマシンがオペレーションを実行します。

目的関数

\text{minimize} \ C_{\max}, \ \ C_{\max}=s_{sink}

フロー整合条件

\sum_{e \in \delta^-(n) \cap E^d} x_e = \sum_{e \in \delta^+(n) \cap E^d} x_e, \ n \in O

\sum_{e \in \delta^-(n)} x_e = 1, \ n \in M

\sum_{e \in \delta^+(n) \cap O(m)} x_e = 1, \ n \in M

全てのオペレーションが処理されること

$\sum_{e \in \delta^+(n) \cap E^d} x_e = 1, \ n \in O$
実行順序制約
同一ジョブ内のオペレーションの順序を守るための制約です。

s_u + t_u \le s_v, \ (u, v) \in E^c

マシン割り当てに関する制約
$s_u + p_u + L(x_e - 1) \le s_v, \ e=(u, v) \in E^d$

参考実装

今回はpulpを利用して、CBCソルバーで上の例を解いてみます。
普通は、JSPで厳密解を求めようとするのはほとんどの場合で無理なので、基本はヒューリスティックソルバーを利用したりなんかが多いです。私はOR-toolsを利用していました。

import pulp as pl
# g: nx.DiGraph
# prob: LpProblem, LpMinimize
# x[e]: e \in Ed, LpBinary
# s[n]: n \in g.nodes, lowBound=0, LpInteger

# 目的関数
prob += s[Consts.sink]

# 制約条件
# 1. フロー整合条件
for o in O:
    prob += (
        pl.lpSum([x[e] for e in g.in_edges(o) if e in Ed])
        - pl.lpSum([x[e] for e in g.out_edges(o) if e in Ed])
        == 0,
        f"flow_conservation_{o}",
    )

for m in jsp.machines:
    prob += (
        pl.lpSum([x[e] for e in g.out_edges(m)]) == 1,
        f"machine_start_{m}",
    )

    prob += (
        pl.lpSum([x[e] for e in g.in_edges(Consts.sink) if e[0].machine == m]) == 1,
        f"machine_end_{m}",
    )


# 2. すべてのオペレーションが処理される
for o in O:
    prob += pl.lpSum([x[e] for e in g.in_edges(o) if e in Ed]) == 1, f"operation_{o}"


# 3. 実行順序制約
for u, v in Ec:
    prob += s[u] + g.nodes[u]["t"] - s[v] <= 0, f"conjunctive_{u}_{v}"


# 4. マシン割り当てに関する制約
for u, v in Ed:
    prob += (
        s[u] + g.nodes[u]["t"] + Consts.L * (x[u, v] - 1) <= s[v],
        f"disjoint_{u}_{v}",
    )

解いた結果
Objective: 13.00

$M_1$ : $O_{2,1}$ (1:00 ~ 4:00) → $O_{1,1}$ (4:00 ~ 6:00) → $O_{3,1}$ (6:00 ~ 7:00)
$M_2$ : $O_{1,2}$ (0:00 ~ 4:00) → $O_{2,2}$ (4:00 ~ 7:00) → $O_{3,2}$ (7:00 ~ 10:00)
$M_3$ : $O_{3,3}$ (0:00 ~ 4:00) → $O_{1,3}$ (6:00 ~ 9:00) → $O_{2,3}$ (9:00 ~ 13:00)

ベンチマークとか

http://jobshop.jjvh.nl/index.php
ここに扱いやすいJSPのベンチマークとその解が上がっています。
上でも書いた通り、厳密解として求めることは難しいと思います。
詳細は書きませんが、10ジョブx10マシンをGUROBIソルバー, 4スレッド実行で30分やってもMIP-GAPは80%程度にしかなりません。

Fusic 技術ブログPublication

さまざまな個性を受け入れて有機的につなぐ社内環境を整える。あらゆる事業機会の創出と実現を繰り返し、世の中に対する視点を絶えず増やして成長していく。あっと驚くような角度から発展できるポイントを見つけ、そこにいい感じにフィットする形でテクノロジーを組み込んで、世の中をちょっとずつ、時には大胆にアップデートしつづけていく。