つくってわかるFreeモナド 〜 Freeモナド、その仕組み 〜
はじめに
Freeモナド・・・使ってますか?
使ってないという方も、Freeモナドが使われたフレームワークやライブラリを使っていて間接的に使っているかもしれません。
例えばフレームワークだとHalogenやJellyなど、ライブラリだとRun(拡張可能作用)で使われています。
newtype HalogenM state action slots output m a = HalogenM (Free (HalogenF state action slots output m) a)
newtype ComponentM m a = ComponentM (Free (ComponentF m) a)
newtype Run r a = Run (Free (VariantF r) a)
この記事は、そのFreeモナドの仕組みを理解するため、Freeモナドを実際に作りながら解説や図解をしていくという記事です。
実用的なライブラリとしてのFreeモナドをつくるのは大変ですが、あそびながら理解するために最低限のものをつくるという趣旨なら、意外と短いコード量でもいけるので、気楽にやってみましょう!
つくる
Freeモナドをつくる道筋
こんな感じで進めていきます。
- 型を定義する
- モナドにする
- あそぶ
Free型を定義しよう
最初のステップとして、Freeの型を定義しましょう。
次のような代数的データ型を定義します。
data Free f a
= Pure a
| Free (f (Free f a))
1行目・2行目で「ふむふむ」となり、3行目で「うっ」となったかもしれません。
が、ご安心ください。よく見れば同じ構造が再帰的に定義されているだけです。
Freeが3つも出てきて混乱するかもしれませんが、1つは単なるデータ構築子です。
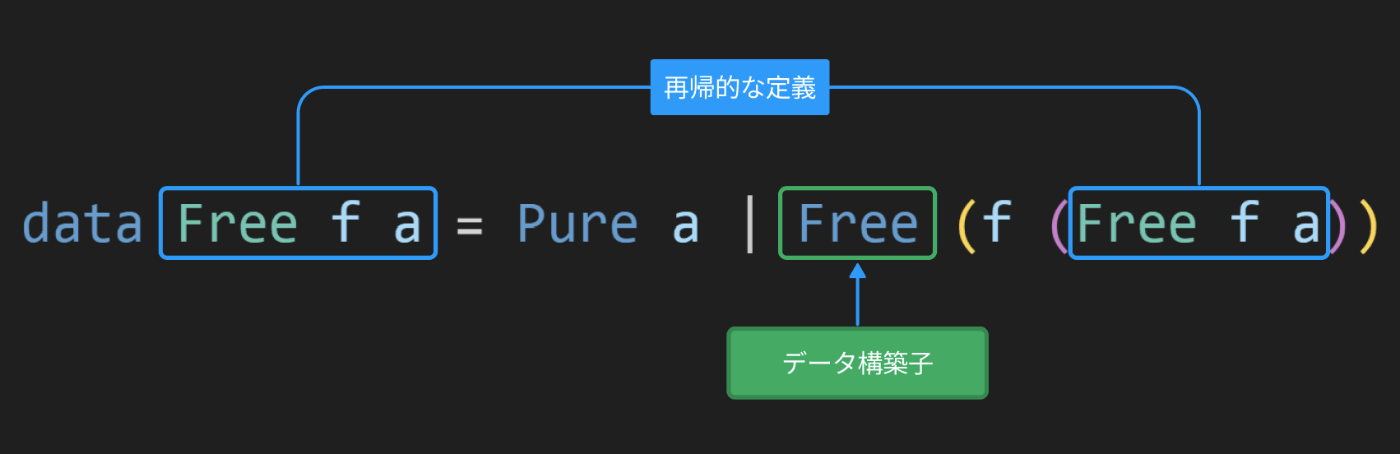
データ構築子Freeは、再帰的なデータの構築を可能にするもので、Pureは終端を表すものです。
構造の持つ意味
上述したように、型構築子Free f aに対し、データ構築子Pure aは構造の終端を表す部分で、aを持っています。
データ構築子Free (f (Free f a))の方は再帰的な構造を実現している部分で、様々なfの値を階層的に蓄積していってる部分です。
様々なfの値というのは、例えば次のような代数的データ型TeletypeにおけるPutStrLnやGetLineの値のことです(これはPureScriptのFreeモナドのライブラリであるpurescript-freeの例で使われている型です)。
data Teletype a = PutStrLn String a | GetLine (String -> a)
このfは「何を行うか」を表すインタフェースのようなもので、ネストしていった階層の深さが処理の順序にあたります。
説明しやすくするため、上記の型をFree f aのfとして、値を作ってみます。
(あまりネストが深くなると見づらくなるのでこの程度にとどめています。また実用する上ではこんな作り方はしないです)
derive instance teletypeFunctor :: Functor Teletype
t :: Free Teletype Unit
t = Free (GetLine (\line -> (Free (PutStrLn line (Pure unit)))))
1階層目のGetLineが最初の処理で、2階層目(終端)のPutStrLnが次の処理にあたります。
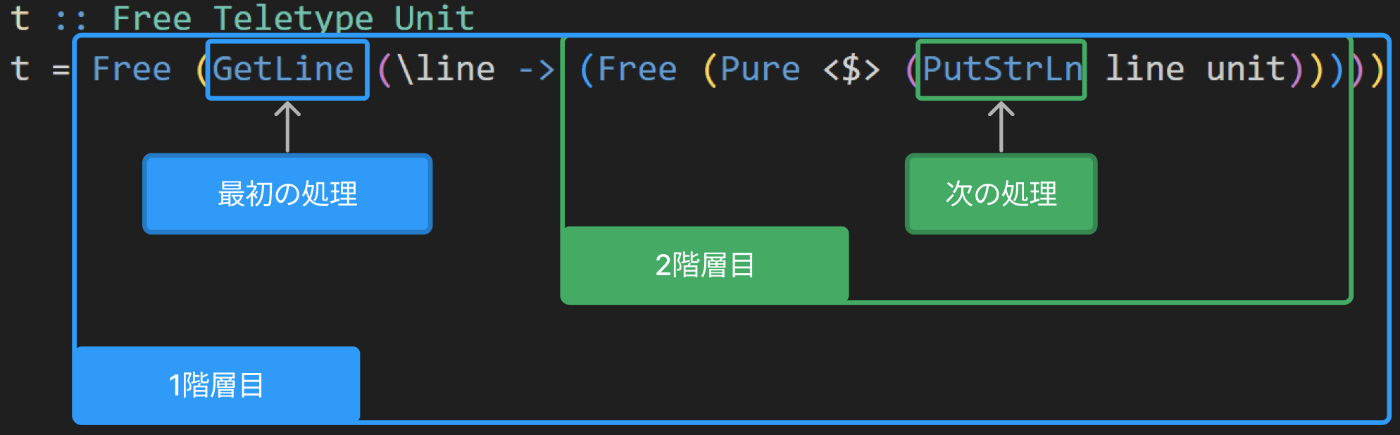
このように、階層構造とインタフェース的役割を持つデータ型を使って、ときには上記よりもっと複雑になる処理の順序・流れを蓄積しつつも、型としてはFree f aとシンプルに表すことができるのがFreeモナドの特徴の一つです。
この例のGetLineやPutStrLnの具体的な処理は、この構造の構築とは切り離されており、別に定義することになります。
この「分離されている」というところがFreeモナドの素晴らしいところです。
DSLが簡単に作れるのもこの特性のおかげでしょう。
ところで、上記例においてPutStrLn String aのaや、GetLine (String -> a)の(String -> a)が何か気になった方がおられるかもしれません。
これらは処理の結果を後続の処理に渡すための仕組みです。
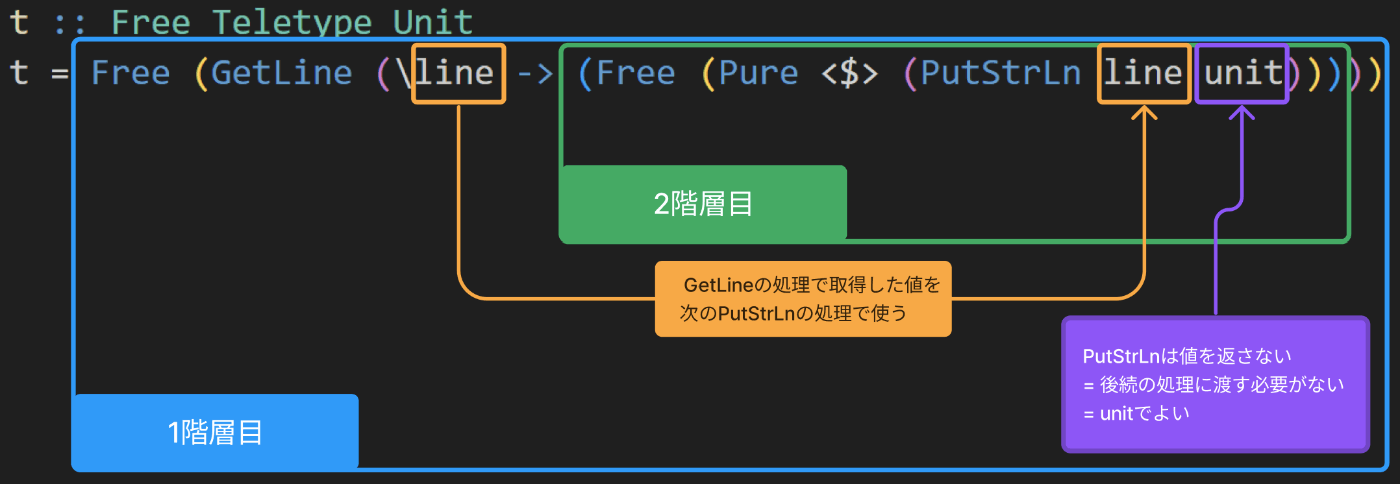
このような構造において、処理結果を後続の処理に渡すために、こういったアプローチをとっているわけです。
GetLineがもっている関数に型アノテーションをつけてみると、GetLineが持っている関数の型がよくわかるでしょう。
t :: Free Teletype Unit
t = Free (GetLine
((\line -> Free (PutStrLn line (Pure unit)))
:: (String -> Free Teletype Unit))
)
ところで、Freeの値をつくるのにいちいちこんな風に書きたくはないですよね?
Free (GetLine (\line -> (Free (PutStrLn line (Pure unit)))))
こんな風に書けたらいいな、そうは思いませんか?
t :: Free Teletype Unit
t = do
line <- getLine
putStrLn line
・・・・・・思うでしょう?
思いますね!
(Freeモナドをよくご存じの方にとっては茶番でしょうが、話の流れの都合ってやつです)
んじゃ、書けるようにしましょうー。
どうしたらいいかってーと、Freeをモナドにすればいいのです!
Freeをモナドにしよう
モナドにすればいいのです!と言いましたが、そもそも今回はFreeモナドの話をしていたわけで、
最初から既定路線でした。
しかし、ここまでのコード上では、ただ型が定義されただけなので、当然モナドではありません。
ということで、Freeをモナドにしたいのですが、PureScriptで、ある型をモナドとして扱えるようにするためには、その型がいくつかの型クラスのinstanceになっている必要があります。
その型クラスとは、Functor Apply Applicative Bind Monadです。
これらの型クラスには次のように階層的な関係性があります。
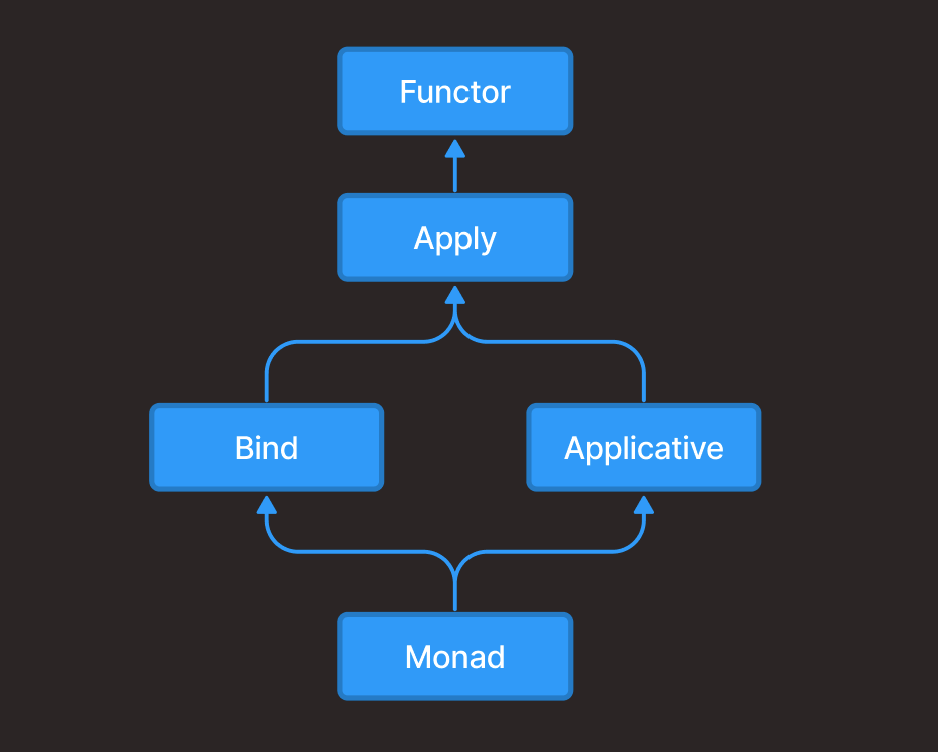
図でいうと、Functorが階層のトップにいるので、まずFunctorからいってみましょう。
Functor
FreeをFunctorのinstanceにします。
定義はこのようになります(実装はこれからです)。
実装のイメージがつきやすいようmapに型アノテーションをつけています。
instance functorFree :: Functor (Free f) where
map :: forall a b. (a -> b) -> (Free f a) -> (Free f b)
Free f aのaをbに写してますね。
FreeにはPureとFree2つのデータ構築子が存在するので、次のようにそれぞれのパターンの処理を実装することになります。
instance functorFree :: (Functor f) => Functor (Free f) where
map :: forall a b. (a -> b) -> (Free f a) -> (Free f b)
map fn (Free f) = Free (map fn <$> f)
map fn (Pure a) = Pure (fn a)
着目したいポイントは、型制約Functor fの部分です。
この制約がなぜ必要かは、Free (map fn <$> f)の部分を見れば理解していただけると思います。
<$>はmapなので、fのmapを使うために必要なわけです。
この部分の解説をしましょう。
この部分をletと型アノテーションを使ってクッソ冗長に書きなおしてみます。
map fn (Free free) = let
freeMapFn = map fn :: (Free f a) -> (Free f b)
f = free :: (f (Free f a))
in Free (freeMapFn <$> f)
最初のmap fnの部分ですが、mapは自分自身の関数であるため、再帰的な呼び出しとなります。
そしてmapにはfnしか渡していないので、結果は(Free f a) -> (Free f b)という関数になります。
次に(Free free)のfreeは、定義から(f (Free f a))となるので、mapの結果の関数をfreeMapFn <$> fというように使えます。
Freeの方の実装が比較的複雑だったのに比べ、Pureのmapの実装は非常に単純で、fn aの結果をPureに包んでるだけです。
このmapがどう動作するのか、この簡単なFreeの値を使って説明します。
f :: Free Maybe String
f = Free (Just (Free (Pure <$> (Just "hoge"))))
exec :: Free Maybe String
exec = (_ <> ":fuga") <$> f
まず最初は
map fn (Free free) = let
freeMapFn = map fn :: (Free f a) -> (Free f b)
f = free :: (f (Free f a))
in Free (freeMapFn <$> f)
の方にマッチしますね(説明のため冗長なコードの方をもってきてます)。
この場合のFree freeのfreeは、Just (Free (Pure <$> (Just "hoge")))です。
そしてMaybeのmapによって、freeに対してfreeMapFnが実行されます。
freeMapFnの元になっているfnは最初渡された関数です。
そしてfreeMapFnの元になっているmapはFreeのmapです。
更に値はFree (Pure <$> (Just "hoge"))となります。
Freeのmap関数に、Freeの値が与えられました。
はい、再帰です。
次は
map fn (Pure a) = Pure (fn a)
の方にマッチします。
ここでaの値は"hoge"なので最初渡したmapの関数(_ <> ":fuga")によって文字列が結合され、aの値はhoge:fugaとなります。
Functorの説明はこれくらいでよいでしょう。
FreeにFunctorが必要な理由がご理解いただけたと思います。
Applicative
Applicativeのinsntanceはめちゃくちゃ簡単です。
Pureを使うだけです。
instance applicativeFree :: (Functor f) => Applicative (Free f) where
pure = Pure
以上。
Bind
Bindのinstanceはこうです。
説明のためbindの型アノテーションも書いています。
instance bindFree :: (Functor f) => Bind (Free f) where
bind :: forall a b. Free f a -> (a -> Free f b) -> Free f b
bind (Free f) fn = Free $ (\a -> bind a fn) <$> f
bind (Pure a) fn = fn a
まずbind (Free f) fn = Free $ (\a -> bind a fn) <$> fの方の説明をします。
型制約によりfはFunctorなので<$>が使えます。
その際のmap関数(\a -> bind a fn)のaはFreeなので、元の関数fnを維持したままbindで再帰します。再帰していった結果、終端であるPure aの方にマッチしたらfn aして終わりです。(\a -> bind a fn) <$> fの結果はFreeに与えられるので、bindするたびFreeの階層はどんどん増えていきます。
つまり、bindにより、値を作る際にFreeをネストさせなくてよくなります。
こんなコードを書かなくてよくなります(よかった)。
t :: Free Teletype Unit
t = Free (GetLine (\line -> (Free (Pure <$> (PutStrLn line unit)))))
これまで作ってきたpureや>>=を使うと↑を↓のように書けるようになります。
t :: Free Teletype Unit
t = (Free $ pure <$> (GetLine identity))
>>= (\line -> Free $ pure <$> (PutStrLn line unit))
複数の小さなFreeがbindでくっついた形になりました。
GetLineとPutStrLnがバラされたので、GetLineの関数はFreeを返さなくてよくなりました。型的に取得したものをそのまま返せばいいのでidentityでよいのです。
(なぜidentityでよいのか、なぜこのような関数が必要なのかは、このあと解説します)
別関数に切り出して、型アノテーションを書いてみるとわかりやすいでしょう。
getLine :: Free Teletype String
getLine = Free $ pure <$> (GetLine identity)
putStrLn :: String ->Free Teletype Unit
putStrLn s = Free $ pure <$> (PutStrLn s unit)
t :: Free Teletype Unit
t = getLine >>= (\line -> putStrLn line)
Bindの解説
bind関数は極めて重要なので、getLine >>= (\line -> putStrLn line)を例にとり、処理の流れを解説しましょう。
ここでGetLine identityのidentityの意味もわかります。
getLineが示す値は構造がわかるように書くとFree (GetLine (\a -> Pure (identity a)))です。なので、bindとしては次のパターンにマッチします。
bind (Free f) fn = Free $ (\a -> bind a fn) <$> f
このときのfはGetLine (\a -> Pure (identity a))となっています。
次にfに対しての<$>つまりmapの動きを説明します。
Functorはderive instanceで導出できるのですが、説明のため敢えて書くとこんな感じになるでしょう。
instance teletypeFunctor :: Functor Teletype where
map fn (PutStrLn s a) = PutStrLn s (fn a)
map fn (GetLine next) = GetLine $ fn <<< next
このmap fn (GetLine next)の部分をいまの値で置き換えてみると、このようになります。
map (\a -> bind a (\line -> putStrLn line)) (GetLine (\a -> Pure (identity a)))
GetLine $ fn <<< nextの部分を上記の値で置き換えてみると、次のような値が返されることがわかります。
GetLine $ (\a -> bind a (\line -> putStrLn line)) <<< (\a -> Pure (identity a))
整形してみるとこうです。
GetLine (\a -> (Pure (identity a)) >>= (\line -> putStrLn line))
(\a -> bind a fn) <$> fの結果はFreeに渡されるので、最終的に返る値はこうなります。
-- 型はFree Teletype Unit
Free (GetLine (\a -> (Pure (identity a)) >>= (\line -> putStrLn line)))
putStrLnの部分を構造がわかるように戻すとこうなります。
Free (GetLine (
\a -> (Pure (identity a)) >>= (\line -> Free (PutStrLn line (Pure unit)))
))
ここでidentityの意味がわかります。
まずそもそもGetLineがString -> a型の関数を持っていなかった場合、後続の処理に値を渡すことができないです。
aのような任意の型を返す必要があるのは、状況によって返す型が変わるからですね。
最初GetLineはFree Teletype String型でString型を返すようになっていました。
それが、bindの処理の中でmap関数によりFree Teletype Unitを返すようになりました。
なのでくどいですが、GetLineは関数を持っていなければなりません。
そしてgetLineのように組み合わせ前提の単純なFreeを返す場合、「関数でなければならない」「その関数はStringを返す」という条件を満たすものとしてidentityは都合がよいのです。
getLine :: Free Teletype String
getLine = Free $ pure <$> (GetLine identity)
これがGetLineが持っている関数がidentityだった理由です。
bindの話が途中でした。
上記の(Pure (identity a)) >>= (\line -> Free (PutStrLn line (Pure unit)))の部分もまたbindを呼び出しているので、ここも展開してみようと思います。
(関数の中で呼ばれるので本当は評価は後なのですが、説明のため)
この場合のbindはPureのパターンにマッチします。
bind (Pure a) fn = fn a
これにさきほどのコードの値を当てはめて置き換えていってみます。
fnが(\line -> Free (PutStrLn line (Pure unit)))で、aが(identity a)なのでこうなります。
(\line -> Free (PutStrLn line (Pure unit))) (identity a)
↓
(\line -> Free (PutStrLn line (Pure unit))) a
↓
Free (PutStrLn a (Pure unit))
ここまできたところで、元のコードに上記を埋め込んでみます。
Free (GetLine (\a -> Free (PutStrLn a (Pure unit))))
・・・・・・どこかで見た形ですね?
そう、この記事の最初の方で
「ところでFreeの値をつくるのにいちいちこんな風に書きたくはないですよね?」
と言っていた形と全く同じです。
ついにやりました!
・・・・・・さて、この項においては、面倒な方法でつくる値と同じ値を、簡単につくれるようになったことを説明しました。
長い長いBindの説明もこれで終わりです。
さぁもう一息です。次にいきましょう。
(まだ見づらい部分に関してはもう少しあとに解決させます)
Monad
Monadは型クラスの定義がこうなっているため、ApplicativeとBindのinstanceになってさえいれば特に実装はいらないです。
class (Applicative m, Bind m) <= Monad m
Apply
Applyの実装も簡単です。Monadのinsntanceになっていれば使えるapがそのまま使えるからです。
instance applyFree :: (Functor f) => Apply (Free f) where
apply = ap
お疲れ様でした!
これにてようやくFreeがモナドになりました。
使ってみよう
できたので使ってみましょう。
Freeを簡単につくれるようにしよう
さて、できあがったFreeを使いたいのですが、Freeをつくるのが面倒です。
上述したようにこんなことやってられません。
data Teletype a = PutStrLn String a | GetLine (String -> a)
program :: Free Teletype Unit
program = (Free $ pure <$> (GetLine identity))
>>= (\line -> Free $ pure <$> (PutStrLn line unit))
ということで、こんな関数を作ります。
↑のコードでFreeをつくっている部分をそのまま関数にした感じです。
liftF :: forall f. Functor f => f ~> Free f
liftF f = Free $ pure <$> f
これは任意のFunctorをFreeに「持ち上げる」関数です。
これを使うと上記のコードはこうなります。
program :: Free Teletype Unit
program = liftF (GetLine identity) >>= (\line -> liftF (PutStrLn line unit))
do記法にした方が見やすいでしょう。
program :: Free Teletype Unit
program = do
line <- liftF (GetLine identity)
liftF (PutStrLn line unit)
更に、liftF GetLineやliftF PutStrLnを別の関数にするとこうなります。
putStrLn :: String -> FreeTeletype Unit
putStrLn s = liftF $ PutStrLn s unit
getLine :: FreeTeletype String
getLine = liftF $ GetLine identity
program :: Free Teletype Unit
program = do
line <- getLine
putStrLn line
で き た !
上~の方で書いていた理想形になりました!
あそぼう
GetLineやPutStrLnはあくまでインタフェースのような役割なので、対応する実装を与えないといけません。実装は自由にできるのですが、今回はこのような実装を用意してみました。
run :: Free Teletype ~> Effect
run (Pure a) = pure a
run (Free (PutStrLn s a)) = log s >>= \_ -> run a
run (Free (GetLine k)) = run $ k "FreeExample: fake input"
単にパターンマッチをして、Effectに自然変換しているだけです。
使うのは簡単で、こんな感じです。
main :: Effect Unit
main = do
run program -- FreeExample: fake input
FreeExample: fake inputという出力が得られました。
では、programをrunに与えたとき、どのように処理が進んだ結果、この出力が得られたのか、それをこれから説明します。
まずは説明のために、programの値をdo記法もbindも使わない形に戻します。
program :: Free Teletype Unit
program = Free (GetLine (\line -> (Free (PutStrLn line (Pure unit)))))
これをrunに与えます。
すると、このパターンにマッチします。
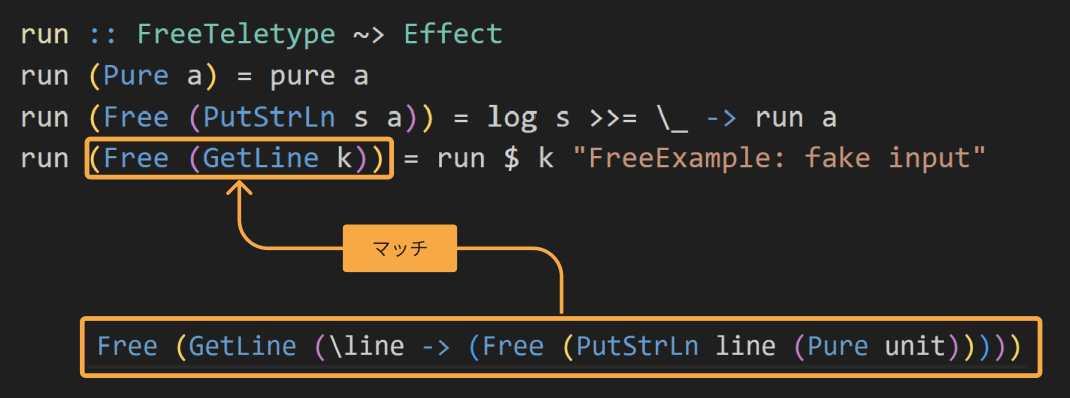
GetLineのkは関数ですが、その内容はこうなっていますね。
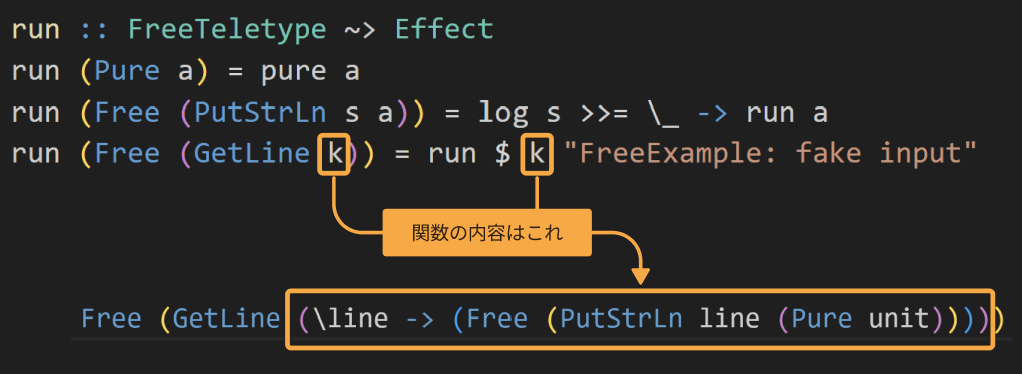
そのkに入力を与えた結果は、Free (PutStrLn "FreeExample: fake input" (Pure unit))になります。
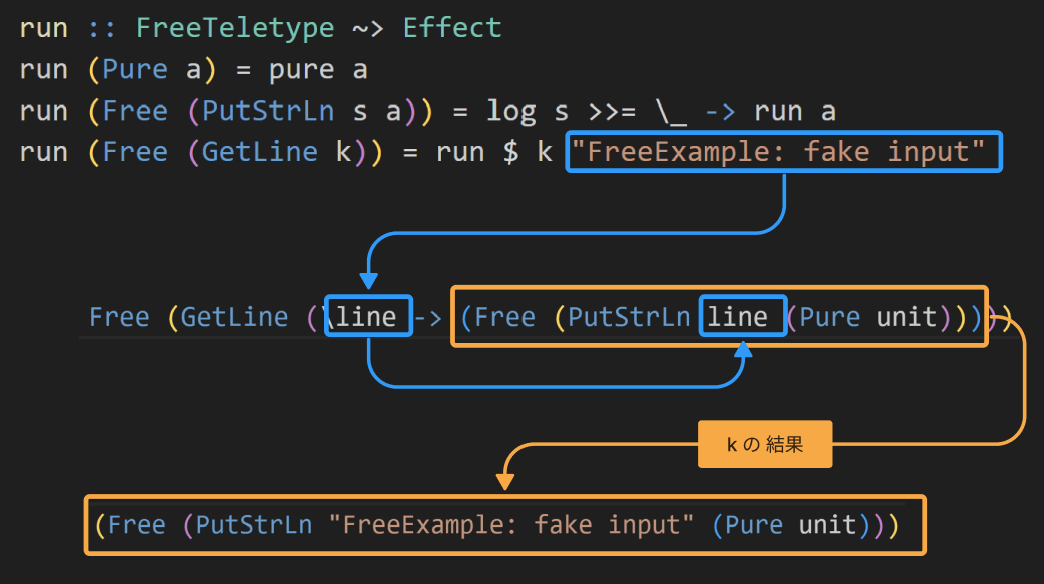
この値はrunの再帰呼び出しに渡ります。今度はどのパターンにマッチするでしょうか?
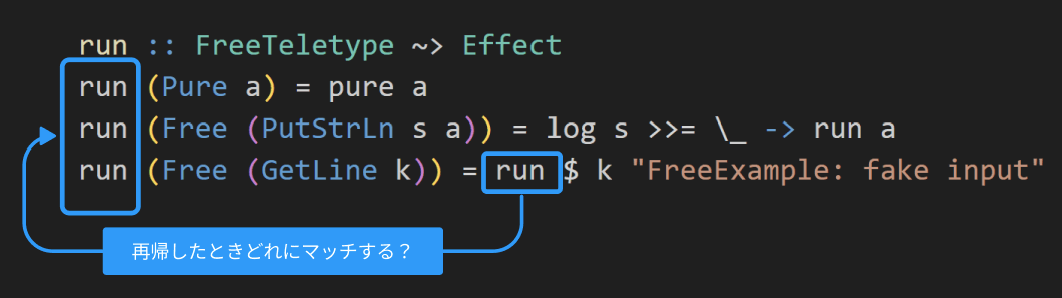
当然Free PutStrLn...にマッチしますね。
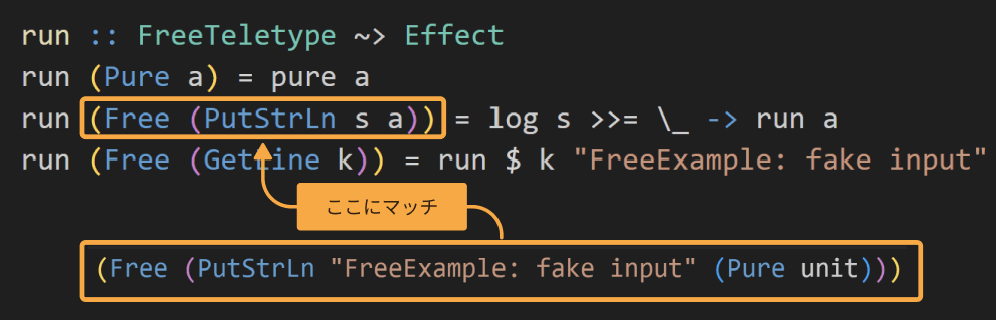
PutStrLnの値はそれぞれこうなっています。
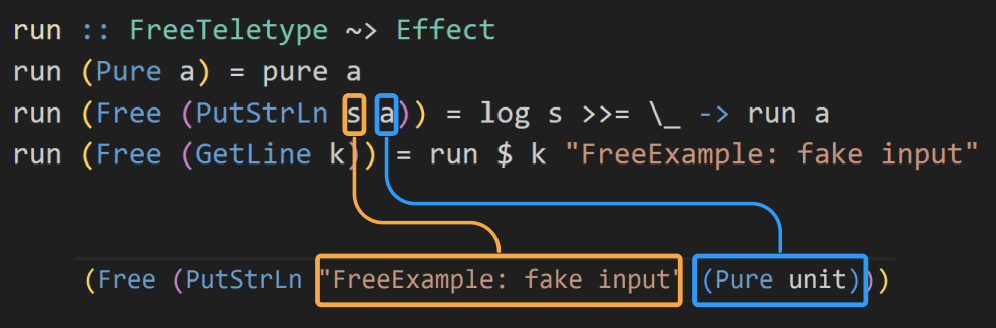
つまりこういうことです。文字列をログ出力した後、またrunの再帰呼び出しです。
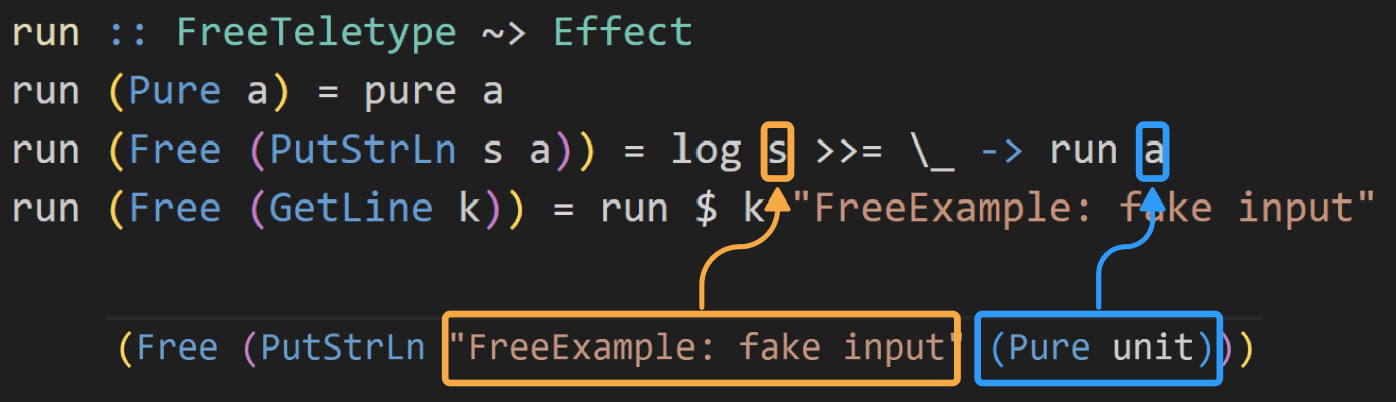
次はFree Pureにマッチするので、pure unitを返して終わりです。
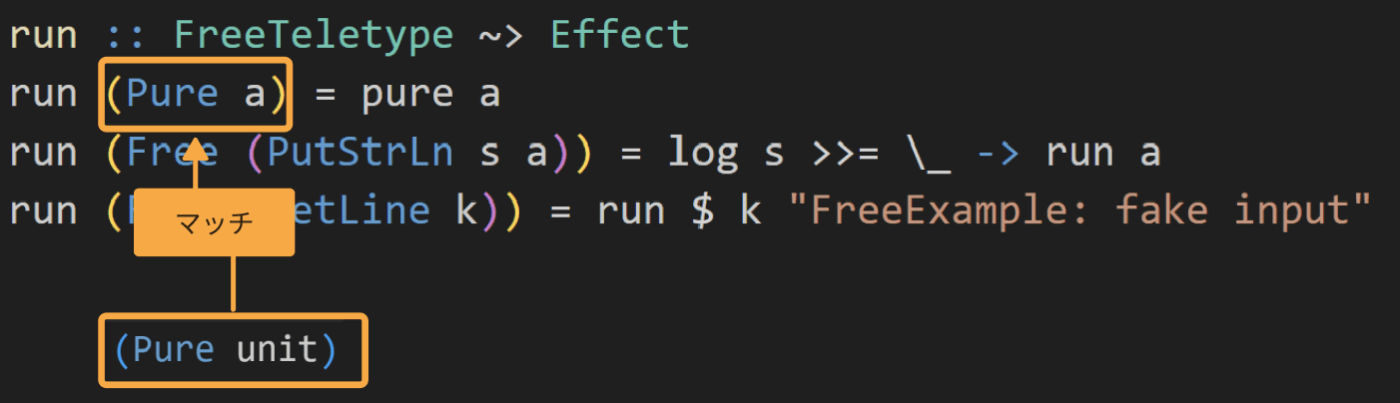
処理の流れの説明は以上になります。
で、上記のようにFreeのレベルでパターンマッチをしてもいいのですが、次のような関数があると便利です。
foldFree :: forall f m. MonadRec m => (f ~> m) -> Free f ~> m
foldFree k = tailRecM go
where
go :: forall a. Free f a -> m (Step (Free f a) a)
go f = case f of
Pure a -> Done <$> pure a
Free g -> Loop <$> k g
結局構造を再帰的に辿るということをやってます。
辿る部分を共通的な関数にしたということですね。
これを使うとFreeのパターンマッチが消せます。
run :: FreeTeletype ~> Effect
run = foldFree go
where
go :: Teletype ~> Effect
go (PutStrLn s a) = const a <$> log s
go (GetLine k) = pure (k "SimpleFreeExample: fake input")
FreeでReaderモナドをつくってみよう
せっかくなので、Freeを利用してReaderモナドをつくってみるおまけを載せておきます。
newtype ReaderF r e = ReaderF (r -> e)
derive newtype instance functorReaderF :: Functor (ReaderF r)
type FreeReader r a = Free (ReaderF r) a
ask :: forall e. FreeReader e e
ask = liftF (ReaderF identity)
local :: forall r a. (r -> r) -> FreeReader r a -> FreeReader r a
local f r = map f ask >>= pure <<< runReader r
asks :: forall e a. (e -> a) -> FreeReader e a
asks f = f <$> ask
runReader :: forall r a. FreeReader r a -> r -> a
runReader f e = case resume f of
Left (ReaderF r) -> runReader (r e) e
Right a -> a
-- Freeのレイヤーを一つunwrapする
-- PureならRightが返り、FreeならLeftが返る。
resume
:: forall f a
. Free f a
-> Either (f (Free f a)) a
resume = resume' (\g -> Left g) Right
-- Freeのレイヤーを一つunwrapする
-- こちらはデータ型によって適用する関数を指定することができる
resume'
:: forall f a r
. (f (Free f a) -> r)
-> (a -> r)
-> Free f a
-> r
resume' k j f = case f of
Free g ->
k g
Pure a ->
j a
type Config = { debug :: Boolean }
spec :: Spec Unit
spec = do
describe "Readerのテスト" do
describe "ask" do
it "環境を取得できる" do
"value" `shouldEqual` runReader ask "value"
describe "asks" do
it "環境を取得する際に渡した関数で環境の値を変更することができる" do
"value added" `shouldEqual` runReader (asks (_ <> " added")) "value"
describe "local" do
it "環境の変更を、渡した関数内のスコープに閉じることができる" do
let
getFlag :: FreeReader Config Boolean
getFlag = do
_ <- local (\c -> c { debug = true }) do
-- ここでaskするとdebugはtrueになってる。
pure false -- 説明のためだけの処理なので適当な値を返す
c <- ask
pure c.debug
runReader getFlag { debug: false } `shouldEqual` false
全体像
つくったFreeの全体像を載せます。
案外短いことがわかると思います。
import Prelude
import Control.Monad.Rec.Class (class MonadRec, Step(..), tailRecM)
import Control.Monad.Trans.Class (class MonadTrans)
import Data.Either (Either(..))
import Data.Maybe (Maybe(..))
data Free f a = Pure a | Free (f (Free f a))
instance functorFree :: (Functor f) => Functor (Free f) where
map :: forall a b. (a -> b) -> (Free f a) -> (Free f b)
map fn (Pure a) = Pure (fn a)
map fn (Free f) = Free (map fn <$> f)
instance applyFree :: (Functor f) => Apply (Free f) where
apply = ap -- apはMonadであれば使える関数
instance applicativeFree :: (Functor f) => Applicative (Free f) where
pure = Pure
instance bindFree :: (Functor f) => Bind (Free f) where
-- あえてアノテーションを書くとこう
bind :: forall a b. Free f a -> (a -> Free f b) -> Free f b
bind (Pure a) fn = fn a
bind (Free f) fn = Free $ (\a -> a >>= fn) <$> f
instance monadFree :: (Functor f) => Monad (Free f)
-- 任意のFunctorをFreeに持ち上げる
liftF :: forall f. Functor f => f ~> Free f
liftF f = Free $ pure <$> f -- Free (Pure a) という状態
-- 渡された自然変換関数(f ~> m)を使い、`Free f a`から`m a`に変換して返す。
-- `m`は末尾再帰モナドとなる
foldFree :: forall f m. MonadRec m => (f ~> m) -> Free f ~> m
foldFree k = tailRecM go
where
go :: forall a. Free f a -> m (Step (Free f a) a)
go f = case f of
Pure a -> Done <$> pure a
Free g -> Loop <$> k g
-- Freeのレイヤーを一つunwrapする
-- PureならRightが返り、FreeならLeftが返る。
resume
:: forall f a
. Free f a
-> Either (f (Free f a)) a
resume = resume' (\g -> Left g) Right
-- Freeのレイヤーを一つunwrapする
-- こちらはデータ型によって適用する関数を指定することができる
resume'
:: forall f a r
. (f (Free f a) -> r)
-> (a -> r)
-> Free f a
-> r
resume' k j f = case f of
Free g ->
k g
Pure a ->
j a
おわりに
私は「なんでこれでこんな動作をするのだろう?」という仕組みに関心があり理解したくなるタイプなのですが、Freeモナドに関しては調べたりコードリーディングだけでは理解できず、写経したり自分で作ったりしてきました。
最初参考にしたのが、今現在のpurescript-freeというライブラリだったのですが、このライブラリの今の実装は(恐らくパフォーマンス問題に対応するため)とても複雑な実装になっており、PureScriptを触り始めたばかりの頃に理解を試みたというのも重なって理解が大変でした。思えばもっと単純なところから少しずつ理解していくべきだったのですね(実際結局そうやることになった)。
このような体験が背景にあり、この記事を書いてみたのですが、いかがでしたか?
少しでも皆様の理解の助けになっていれば幸いです。
Discussion