ランダムグラフのシミュレーション 〜『自己組織化と進化の論理』から

はじめに

スチュアート・カウフマン著の『自己組織化と進化の論理―宇宙を貫く複雑系の法則』の中にでてくる以下の話をシミュレーションするプログラムを提示したいと思う。

日本経済新聞社版の『自己組織化と進化の論理―宇宙を貫く複雑系の法則』 p105から引用する。

一万個のボタンが、木でできた床の上にばらまかれているところを想像してみよう。ランダムに二つのボタンを選んで、それらを糸でつなぐ。こんどはこのペアを下に置き、さらに二つのボタンをランダムに選ぶ。そして、それを取り上げ糸でつなぐ。これを続けるのであるが、最初はほぼ確実に、以前取り上げたことのないボタンを取り上げることになる。しかし、しばらくすると、ランダムに二つのボタンを取り上げたとき、その片方は、前にすでに選び上げたボタンだったという状況が増えてくる。したがって、この新しく選んだ二つのボタンの間に糸を結ぶとき、結局は三つのボタンがいっしょに結ばれることになる。要するに、一対のボタンをランダムに選んで糸でつなぐ作業を続けていると、しばらくして、ボタンはより大きなかたまり、つまりクラスターへと相互に連結されるようになる。

https://amzn.asia/d/1FkDa98

プログラムの実行結果

上記をシミュレートするプログラムを実行すると、上部に、ボタンと糸を視覚的に表現したものが表示され、下部には、x軸に「糸の数÷ボタンの数」、y軸に「最大クラスター数」を表すグラフ（ランダムグラフと呼ぶらしい）が表示される。

ボタンの数を色々と変化させてみた結果である。

• ボタンの数が20
  

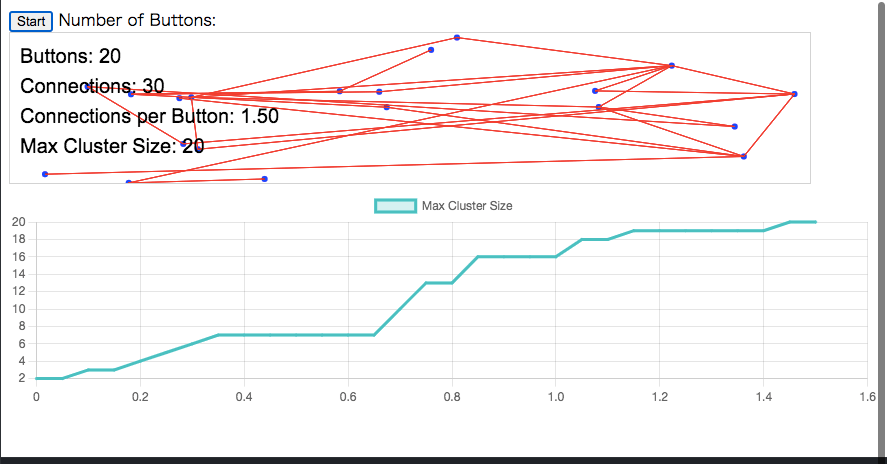
• ボタンの数が100
  

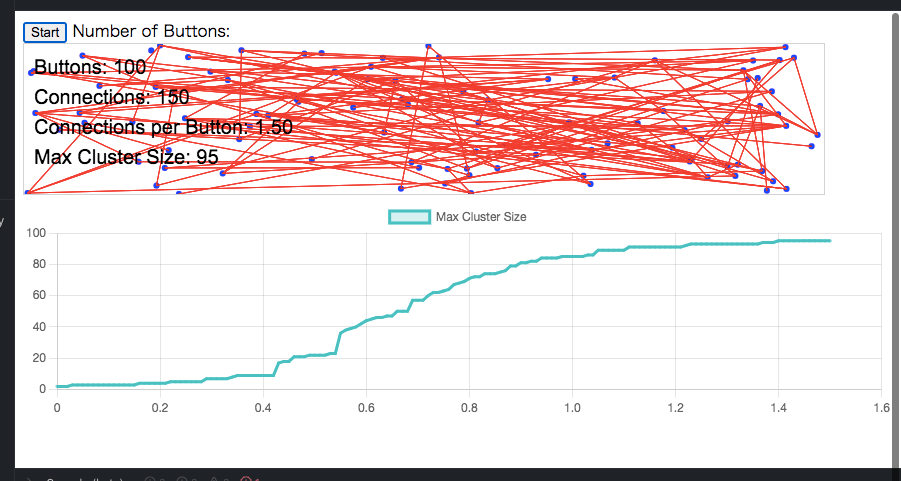
• ボタンの数が400
  

本書によると、x軸が0.5になる辺りから急激な上昇カーブを描くことが記載されているが、確かにそのような傾向が認められる気がする。この急激に様相がかわるのを「相転移」と呼ぶが、著者に言わせると、「この相転移が、生命の起源を導いたのだと信じている。」とのことである。

プログラム

ソースコードは、下記にある。

ボタンの数は、下記を修正すれば可能だ。

const numButtons = 400;