クイックソートを攻略してみた

はじめに

こんにちは！
入社１年目、DXプラットフォーム部エンジニアの松川です。

フォルシアには現在競技プログラミングが好きな社員が多く在籍しています。そこで「競技プログラミングが好きな社員が発信するシリーズ」と題しまして、競技プログラミングに関連する内容を扱っていきます。

ところで、業務、競技を問わず我々がコードを書く際に頻繁に出てくるソートアルゴリズム、これについて普段から意識されている方は少ないかなと思います。もちろん特段内部実装を気にしなくても実用上問題はないのですが、ある特定の実装のソートを攻撃する手段を最近知り、興味深かったのでこの記事ではその quicksort killer と呼ばれる手法とそのアルゴリズムを紹介していきます。

※当たり前ですがこの記事はそのような攻撃を推奨するものではありません。念の為。

前提

quicksort について

quicksort はソートアルゴリズムのひとつで、不安定ソートかつ内部ソートであるなどの性質や、実用上高速であることなどが知られています。
アルゴリズムの手続きとしては Wikipediaがわかりやすいのでご参照ください。

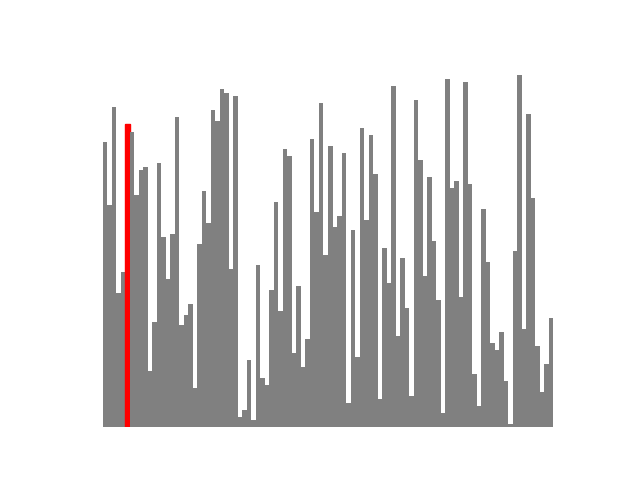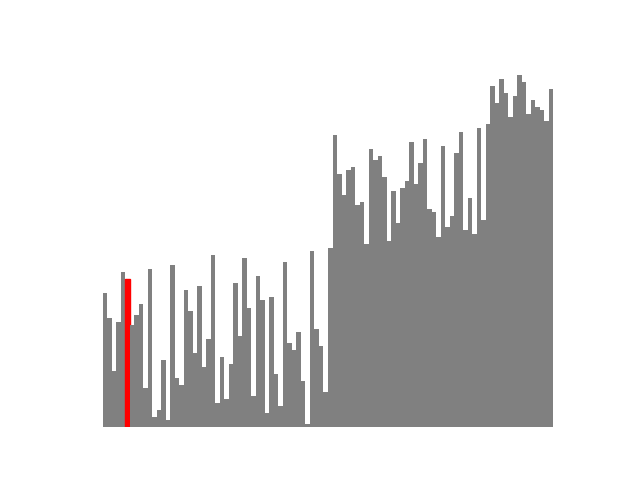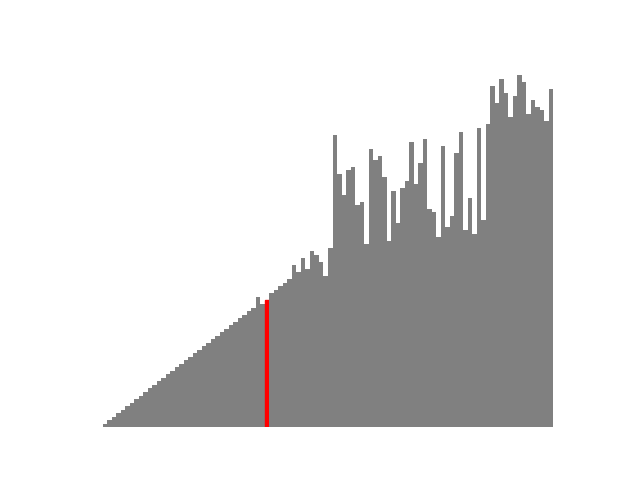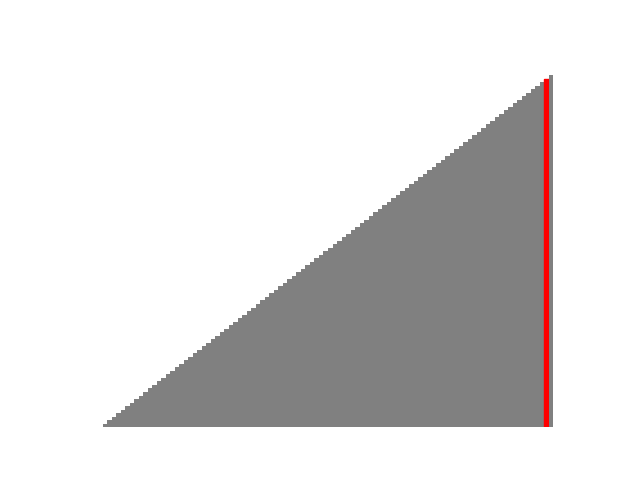
上の図で赤く示されているのが pivot と呼ばれるもので、この pivot を基準にそれより大きいか小さいかを分ける手順を再帰的に繰り返しています。

quicksort の平均計算量はデータ数を$`N`$として$`O(N\log(N))`$ですが、最悪計算量は$`O(N^{2})`$です。
ソートアルゴリズムの文脈なので$`O(N\log(N))`$を"速い"、$`O(N^{2})`$を"遅い"、と読み替えても差し支えありません。
選択される pivot が見ている範囲の中で最小/最大に近くなると分割に偏りが生じ遅くなり、例えば pivot が毎回最小のものが選ばれると選択ソートとほぼ同じ挙動を示し、最悪計算量が達成されてしまいます。

quicksort killer とは？

前項の最悪計算量が$`O(N^{2})`$という部分に注目して、決定的な(入力に対して常に一定の手続きがとられる) quicksort の実装に対して人為的に実行時間が遅くなるような配列を準備すること、あるいはそのアルゴリズムを quicksort killerといい、DoS攻撃や競技プログラミングにおいて他者の解答を撃墜することなどに応用されます。

準備

今回はある quicksort の実装に対してそのインターフェースのみを用いて遅いケースを用意することを試みましょう。

class QuickSortKiller:
    def __init__(self):
        self.candidate = None
        self.keys = dict()

    def compare(self, x, y):
        if (x not in self.keys) and (y not in self.keys):
            if self.candidate == x:
                self.keys[x] = len(self.keys)
            else:
                self.keys[y] = len(self.keys)
        
        if (x not in self.keys):
            self.candidate = x
            return 1
        if (y not in self.keys):
            self.candidate = y
            return -1
        
        return self.keys[x] - self.keys[y]

↑のような class を用意します。ざっくりやっていることを説明すると、先に大小が評価される値がなるべく小さくなるように遅延評価しています。自然な実装であれば pivot は早めに評価されるのでこれにより分割に偏りを生じさせることができます。

QSK = QuickSortKiller()
Arr = list(range(N))
quicksort(Arr, QSK.compare)
ArrInv = [None]*N
for i, a in enumerate(Arr):
    ArrInv[a] = i

↑のようにquicksortの評価関数として先ほど作成した QuickSortKiller のメソッドを持たせて実行します。これでソート済みの配列から手続きが遅いと期待される結果が得られました。これを通常の比較関数に適用するため、つまり結果が(通常の大小比較関数で) ソート済みの配列になるようにするにはこの結果の順列の逆順列をとればよいです。

また、quicksort の実装として

• simple : pivot を見ている範囲の左端とするもの
• med3 : pivot を見ている範囲の左端、中央、右端の中央値とするもの (quicksortの実装例としてよく載っているものです)
• random : pivot を見ている範囲からランダムに選ぶもの

の3つを用意します。

def quicksort_simple(Arr, cmp):
    def _quicksort(left, right):
        if right - left <= 1:
            return
        pivot = Arr[left]
        #[left, i) が pivot 以下になる
        i = left
        pidx = None
        for j in range(left, right):
            if (res := cmp(Arr[j], pivot)) == 0:
                pidx = i
            if res <= 0:
                Arr[i], Arr[j] = Arr[j], Arr[i]
                i += 1
        #どのpivotが選択されても見る配列の長さが1減るようにして停止性を保証する
        Arr[pidx], Arr[i-1] = Arr[i-1], Arr[pidx]
        _quicksort(left, i-1)
        _quicksort(i, right)

    N = len(Arr)
    _quicksort(0, N)

def quicksort_med3(Arr, cmp):
    def _med3(a, b, c):
        if cmp(a, b) > 0:
            a, b = b, a
        if cmp(b, c) > 0:
            b, c = c, b
        if cmp(a, b) > 0:
            a, b = b, a
        return b
    def _quicksort(left, right):
        if right - left <= 1:
            return
        pivot = _med3(Arr[left], Arr[(left+right)//2], Arr[right-1])
        ...(以下同一のため省略)

def quicksort_random(Arr, cmp):
    def _quicksort(left, right):
        if right - left <= 1:
            return
        pivot = Arr[randrange(left, right)]
        ...(以下同一のため省略)

結果

配列の長さを 100 から 2000 まで 50 刻みで 10 回ずつ quicksort を実行した際の平均実行時間を下に示します。比較のためランダムに用意したデータと重ねて表示します。

simple

killer の方は明らかに$`O(N^{2})`$となっています。ちなみにこの場合のキラーケースはソート済みの配列そのものになるので、この実装ではソートを遅くすることを意識していなくても遅くなることが容易に想像されます。

med3

こちらも明らかに$`O(N^{2})`$となっています。縦軸に注目するとキラーケースでの実行時間は simple に比べて高速になっていますが、これは3つの中央値を計算するときに比較関数が呼び出されるので、その分キラーケースとしての最適性が落ちたことが要因であると推察されます。

random

上の2つとは打って変わってキラーケースとして機能していないのが分かります。
この実装でも運が極端に悪ければ$`O(N^2)`$の計算量がかかりますが、乱数が真の乱数で比較関数が通常のものであれば人為的にキラーケースを用意することは不可能です。
(ちなみに、遅延評価をしているのでこの実装でもQuickSortKillerの比較関数を持たせると常に最悪計算量に近い計算量になります)

さいごに

組み込みソートが quicksort をもとにしている多くの言語の実装においては pivot の選択がランダムであったり、再帰が一定まで来たら最悪計算量が保証されるようソートアルゴリズムを heap sort に切り替える introsort などが用いられているのでそのような言語の場合強く意識する必要はありません。ただ Java のプリミティブ型のソートなどはこの方法で攻撃できるので頭の片隅に置いておくと役立つ日が来るかもしれません。

参考

https://igoro.com/archive/quicksort-killer/