正規表現専門家がエンジニアになって正規表現がわからなくなった話
はじめに
こんにちは!新卒1年目エンジニアの宮本唯です。
私はフォルシア入社前にプログラミングの経験はほぼなく、大学では数学科に所属していました。数学の中でも比較的コンピューターサイエンスに近い分野で、主に正規表現が研究対象でした。残念ながら私には研究者としての資質が無かったためエンジニアに転向したのですが、いざエンジニアになってみるとプログラミングで正規表現を扱う機会が非常に多いことが分かります。
フォルシアでは新人研修でPostgreSQLを使って簡単な名簿アプリを作るのですが、ここでもSQL文に正規表現を使う必要がありました。
「正規表現はワイの専門や!ほかの同期を出し抜いてブイブイ言わせたるやで!」
そのしばらくあと、私は絶望を味わいます。
「正規表現何もわからないンゴ。。。」
この記事では、数学の研究とプログラミングの現場での正規表現の使われ方の違いや、それらの違いを乗り越えて私がどのようにポスグレ正規表現マスターになったのかを紹介します。
数学の世界の正規表現~正規言語からの導入~
正規表現の歴史は、20世紀中盤、チョムスキーによる形式言語理論にはじまります。自然言語がどのように形式化できるかに興味を持ったチョムスキーの研究に端を発し、正規言語 や 文脈自由言語 といった形式言語の概念が定義されました。
この記事では歴史に深入りしませんが、ともかく正規表現について数学的に理解するためには 言語 の概念を定義する必要があります。
文字セット、文字列、言語
当たり前のことですが、言語を扱うためには文字が必要です。そこで空でない有限集合 Σ を1つ固定しこれを 文字セット とよぶことにします。文字セットはただの集合なので、Σ = { 0, 1 } でも Σ = { a, b } でも Σ ={ 😀, 🤑, 😇 } でも何でも大丈夫です。
つぎに、文字セットの要素を一列に並べたものを 文字列 とよびます。つまり、文字列は
<div style="text-align: center;">
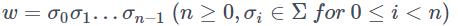
</div>
と表すことができます。
有限個もしくは無限個の文字列の集合のことを 言語 とよびます。たとえば、空集合も言語の1つであるとみなします。
正規表現と正規言語
言語はただの文字列の集まりなので、「はい、これが言語です!」みたいな感じで集合を渡されても非常に使いにくいです。そこで、各々の言語をシンプルに表現するための記法として、 正規表現 があります。
<!--
-
空集合
\emptyset \emptyset - 文字
\sigma \in \Sigma \\{\sigma\\} \sigma - 言語
L_1 L_2 L_1 \cup L_2 L_1 \cup L_2 = \\{ w | w \in L_1 または w \in L_2 \\}
L_1 r_1 L_2 r_2 L_1 \cup L_2 r_1 | r_2 - 言語
L_1 L_2 L_1L_2 L_1L_2 = \\{w_1w_2 | w_1 \in L_1, w_2 \in L_2 \\}
L_1 r_1 L_2 r_2 L_1 L_2 r_1 r_2 - 言語
L L^* $ を L^n L n
L r L^ * r^ *
-->

正規表現は素晴らしい道具に思えますが、残念ながらすべての言語を正規表現で表せるわけではありません。正規表現で表すことのできる言語のことを 正規言語 とよびます。
正規言語の具体例
以下の具体例では文字集合を Σ = { a,b } とします。
<!--
- 文字
a b -
\\{a^nb^m | n,m \geq 0 \\} a^* b^*
-
- 文字
a -
\\{w | wの中に a は偶数回登場する \\}
-
- 最後に、
aabaab bb -
\\{ww | w は文字列\\}
-->

-
プログラミングの世界の正規表現
このように、2種類の正規表現( 空集合、1文字集合 ) に対して3種類の操作(和集合、反復、クリーネ閉包)の組み合わせることで全ての正規表現が記述されます。私はこの数学的な定義を当然のものとして正規表現の研究をしており、きっとエンジニアの使っている正規表現も大した違いはないだろうと高をくくっていました。
ところが、いざプログラミングで正規表現を使おうと思いインターネットで使い方を調べると、操作方法の種類があまりにも多くてびっくり。訳がわからなくなってしまいました。
たとえば、
-
.とか+とか^とか見たことない記号ばかりでてくるけどなんだこれ? - 前方肯定検索、後方肯定検索って普通の正規表現と何が違うの?
- そもそも「マッチする」ってどういう意味で使ってるの?
のような疑問がなかなか解消できませんでした。
それもそのはず、数学とプログラミングでは正規表現を使う目的が違っているため書き方に差があるのです。
数学では正規表現を利用して証明を行い巨大な理論を構築します。もととなる定義が複雑すぎると、1つ1つの証明が煩雑になって理論が汚くなりがちです。そこで、不要なものをそぎ落として定義を簡潔にする傾向があるように思います。
一方、プログラミングでは所望の目的を達成するための道具として正規表現を使います。数学的に表現可能であることが証明されていることよりも、便利な道具を使ってシンプルに記述することの方が大事です。そこで、実用上の目的に対しそれを実現するための操作方法が多数用意されています。
郷に入っては郷に従わなければならないのです。
というわけで、私は数学に自信ニキとしての知識やプライドは捨てなければなりませんでした。しかしながら、大学生活7年間、研究で培ったスキルはきっと生かされるはずです。数学科では実験をする代わりに本を読みます。私が読んできたのは、何が書かれているのかまじで意味不明な専門書の数々です。PostgreSQLには公式ドキュメントがあり、正規表現の使い方も詳しく載っています。よく公式ドキュメントは読みにくいなんて話を聞きますが、わけわからん数学書に比べれば余裕に決まっています。
さあ、PostgreSQL公式ドキュメントを読破してポスグレ正規表現マスターになりましょう!
文字セット Σ の定義
まずは文字セットからです。PostgreSQLでは文字セットはどのように決まっているのでしょうか。
\l コマンドを使うことで、データベースごとの文字セットがわかります。
test=# \x
Expanded display is on.
test=# \l
List of databases
-[ RECORD 1 ]-----+------------------------------
★中略
-[ RECORD 4 ]-----+------------------------------
Name | test
Owner | yui_miyamoto
Encoding | UTF8
Collate | C.UTF-8
Ctype | C.UTF-8
ICU Locale |
Locale Provider | libc
Access privileges |
上記の例では、 データベース test の Encoding(文字セットの符号化形式) は UTF8 となっています。 test の文字セットは UTF8で符号化可能な文字の集合、つまり unicodeです。
unicodeは一般的な文字をほぼカバーしており、例えば𠮷野家の𠮷(unicode U+20BB7)も含まれています。
test=# select substring('𠮷野家', '𠮷') as column;
column
--------
𠮷
(1 row)
数学と違って、文字セットに関してエスケープを考えないといけないのですが、書くと長いので割愛します。
正規表現の文法のほとんどは便利記法
文字セットが無事決まったので、PostgreSQLのドキュメントに書いてある正規表現の定義を書き出してみましょう。かなり長いので、厳密さを犠牲にしたうえで主要な部分を抜粋します。
-
.、 ブラケット式、特別な意味を持たない1文字は正規表現- 特別な意味を持たない1文字はその1文字にマッチする
-
.は任意の1文字にマッチする - ブラケット式
[characters]はcharactersに含まれる任意の1文字にマッチする
- 正規表現の後ろに以下の量指定子をつけたものは正規表現
-
*,*?は0個以上の繰り返し -
+,+?は1個以上の繰り返し -
?,??は0個または1個の繰り返し -
{m},{m}?はm個の繰り返し -
{m,},{m,}?はm個以上の繰り返し -
{m, n},{m, n}?はm個以上n個以下の繰り返し
-
- 正規表現を複数個連結させたものは正規表現
- たとえば、
po+kはpok,pook,poook,... にマッチする
- たとえば、
- 正規表現を
|でつなげたものは正規表現-
ab|abcはabまたはabcにマッチする
-
- 正規表現が一意にパースできるように、括弧
()もしくは(?:)を利用する-
()は 捕捉される括弧、(?:)は 捕捉されない括弧 とよばれる - 捕捉される括弧と捕捉されない括弧の違いは後述
-
ここで (文字列が正規表現に)マッチする という用語を前触れなく使いました。これは、文字列が正規表現に対応する正規言語の要素であること を表しています。
上記の定義のうちいくつかの操作は数学で出てきた正規表現と全く同じものですが、ほかの操作はどういった理解をすればよいのでしょうか。実は、どの操作も別の操作の組み合わせで表現でき、どんな正規表現も最終的に 和集合、結合、クリーネ閉包 の3種類の組合せに還元されるのです。
-
[abc]→a|b|c -
a+→aa* -
a{3}→aaa -
a{2,3}→aa || aaa -
.→a|b|c|d|...(略)- unicodeのありとあらゆる文字が入るので果てしなく長い
-
a?→a | 空集合- 空集合を直接表す正規表現はPostgreSQLにはない
正規表現の操作はたくさんあれど、これらの操作は複雑な表現を単純にするための手段にすぎなかったことがわかりました。
パターンマッチングと正規表現の欲張り属性
プログラミングで正規表現を使う目的の一つに 文字列のパターンマッチング があります。文字列のパターンマッチングとは文字列の中から条件を満たす部分文字列を抽出すること を指しており、このときに指定する条件として正規表現を利用することが多いです。
PostgreSQLでは substring 関数を使ってパターンマッチングができます。
-
substring(文字列, 正規表現): 文字列に対して正規表現にマッチする部分文字列を返す
test=# select substring('spoook','po+k');
substring
-----------
poook
(1 row)
ここからは substring 関数の仕様について詳しく見ていきましょう。
例えば、正規表現にマッチする部分文字列が複数ある場合 substring 関数はどの部分文字列を返すのでしょうか?
答えはドキュメントに書かれていました。
- 正規表現にマッチする部分文字列が複数ある場合は、マッチの開始点が最も前にある部分文字列を返す
- マッチの開始点が最も前にある部分文字列が複数ある場合は、正規表現の 欲張り属性 に依存して返すものが変わる
より詳しく見てみましょう。
ルール1「正規表現にマッチする部分文字列が複数ある場合は、マッチの開始点が最も前にある部分文字列を返す」
test=# select substring('spoook','o+k');
substring
-----------
oook
(1 row)
上の例で、 o+k にマッチする部分文字列は ok, ook, oook の3個ありますが、このうちマッチの開始点が最も早いのは oook です。
ルール2「マッチの開始点が最も前にある部分文字列が複数ある場合は、正規表現の 欲張り属性 に依存して返すものが変わる」
- 正規表現が 欲張り型 の場合は、最も長い部分文字列を返す
- 正規表現が 非欲張り型 の場合は、最も短い部分文字列を返す
正規表現の欲張り属性は次のルールで決定されます。
-
., ブラケット式、他の意味を持たない1文字には、欲張り属性は定義されない- マッチする文字列は常に長さが1なので、定義する必要がない
- 後ろに量指定子がついている正規表現
-
{m},{m}?がついている場合は元の正規表現と欲張り属性が変わらない -
*,+,?,{m,},{m, n}がついている場合は、欲張り型 になる -
*?,+?,??,{m,}?,{m, n}?がついている場合は、非欲張り型 になる
-
- 正規表現を複数連結して作った正規表現は、欲張り属性が定義されている最初の正規表現と欲張り属性が一致する
- 正規表現を
|でつなげて作った正規表現は、必ず 欲張り型 になる
例を2つみてみましょう。
test=# select substring('spoook','po+');
substring
-----------
pooo
(1 row)
-
pは欲張り属性を持たず、o+は欲張り型なので、po+は欲張り型 - したがって、
substring('spoook','po+')はpo,poo,poooのうち最長のpoooを返す
test=# select substring('spoook','po+?');
substring
-----------
po
(1 row)
-
pは欲張り属性を持たず、o+?は非欲張り型なので、po+?は非欲張り型 - したがって、
substring('spoook','po+?')はpo,poo,poooのうち最短のpoを返す
捕捉される括弧、捕捉されない括弧
substring 関数の仕様について理解できたので、色々と遊んでみましょう。勉強したことは遊んで定着させなければなりません。私は「ぽ」という平仮名が好きなので、文字列 spopopopopok に対して正規表現 s(po)+k をマッチングさせてみます。
test=# select substring('spopopopopok','s(po)+k');
substring
-----------
po
(1 row)
ぽ....?????
実は substring 関数にはまだ説明していない仕様があったのです。
正規表現には 捕捉される領域 という概念があります。そして、 substring 関数は正規表現にマッチする文字列のうち 捕捉される領域に対応する部分の文字列 のみ出力することになっているのです。
上記の例の場合、 s(po)+k は spopopopopok 全体にマッチしますが、 s(po)+k の捕捉される領域が po のため出力される文字列は po のみです。
正規表現の捕捉される領域は、使われている () のうち最も左側の () に囲まれた領域を指します。ただし、() が使用されていない正規表現は全体が捕捉されます。正規表現に ()を使う必要がありその()を捕捉したくないときは、捕捉されない括弧 (?: )を使用して捕捉を回避します。
test=# select substring('spopopopopok','s(?:po)+k');
substring
--------------
spopopopopok
(1 row)
この仕様は 肯定前方検索 や 肯定後方検索 の代用となることがあります。
たとえば、メールアドレスの@より後ろの部分をパターンマッチングで抽出することを考えます。
-
waimo_arigato@forcia.kusa→forcia.kusa
@ の取り扱いを工夫する必要があり、普通の正規表現を使うだけでは難しそうですが、捕捉される括弧を使えば以下のように書くことができます。
test=# select substring('waimo_arigato@forcia.kusa','@([a-z.]*)');
substring
-------------
forcia.kusa
(1 row)
完璧ですね。
おわりに
ここまでPostgreSQLのドキュメントを解読し、正規表現を少しでも理解できるよう努力してきました。努力が実を結んだのか、簡単なパターンマッチングであればサクッと実装できる程度にはなることができました。
しかしながら、まだまだPostgreSQLには知らない機能が多くあり、ドキュメントに書いていないこともたくさんあるようです。
ポスグレマスターにはなれそうにないですが、今後はソースコードなども読みつつ、高速検索を支えるエンジニアとしてのキャリアを歩んでいければなと思います。
参考文献
-
オートマトン理論再考
- 正規表現の数学的な定義や具体例の参考としました。後半はかなり専門的ですが、とても興味深い話が盛りだくさんです。
-
PostgreSQL 14.5文書
- PostgreSQL公式ドキュメントは、日本語で最新のものを参考にしました。現在はPostgreSQL15もリリースされ、正規表現についての改善もなされています。
Discussion