拡散モデルのmemorization

今回は, ICLR2026で査読中の以下の論文について見てみます.

https://openreview.net/forum?id=4NfRcEraCw

関連リンク

公式実装はありません.

• arXiv
• OpenReview

書籍情報

断りのない限りは以下の論文から図表を引用します.

Juyeop Kim, Songkuk Kim, and Jong-Seok Lee. How diffusion models memorize, 2025.

はじめに

拡散モデルは多様な画像を高精度に生成できることでしられています. 一方で, 拡散モデルは訓練データを記憶 (memorization)していることが指摘されています. 有名な研究ではGoogleの"Extracting Training Data from Diffusion Models" などがあります.

https://dl.acm.org/doi/10.5555/3620237.3620531

また, あまり知られていない気がしますが, DDPMの査読におけるMeta Reviewでも疑われていたりします.

The FID is very low, maybe some memorization? qualitative experiments are done like nearest neighbor and interpolation, can you add FID on a test set not on the training set to measure memorization?

普段読んでいる概念消去に関する論文は, この現象が観測されないようにするにはどうすればいいのか？という点に焦点を当ててています. 今回は「そもそもなぜ起こるのか？」という点に焦点を当ててみます.

このような研究は当然この論文が最初ではなく, 既存研究が存在しますが, 多くの場合, memorizationを再現することが行われています. 結局のところ, 「なぜ、あるいはどのようにして起こるか」という問いには答えが出ていません.

memorizationとは訓練データと非常に類似している状態ですから, 単純に特定のデータに対して過学習を起こしていると考えることができます. ところが, 著者らは「そんな単純な話ではないよ」ということを主張しています.

この論文では以下の3点についての貢献を挙げています.

1. memorizationは過学習だけでは説明できない. memorizationが発生している状況下では, denoisingの初期段階の損失は実際には大きい（過学習ではない）ことと, memorizationがclassifier-free guidanceによって引き起こされることを示す.
2. ノイズ予測に $-\bold{x}$ を注入し, モデルがdenoisingの過程で正確に $\bold{x}$ を予測するようにmemorizaed promptが誘導している. classifier-free guidanceではこの効果が増幅されて過大評価を起こし, 多様性が低下する.
3. 定式化のために, 中間的な潜在変数のための分解手法を導入する. この分析によって初期のランダム性がどのように $\bold{x}$ に取って代わられるか, そしてスケジュールからの逸脱が記憶の強さとほぼ完全に相関していることを示す.

実験設定

この論文では, 全体を通してStable Diffusion 1.4, 2.1およびRealisticVisionの3モデルを使います. 計算精度はfloat16です. schedulerはDDIMで, 推論ステップ数 $T$ は50, classifier-free guidance (CFG) scale $g$ は7.5です. CFGを使わない場合は1.0とします. Websterから436プロンプトを使って実験を行います. 各プロンプトで $N=50$ 枚のRGB画像を解像度512で生成します. 初期ノイズは一般的な $\bold{x}_T\sim\mathcal{N}(\bold{0}, \bold{I})$ を使用します. 実験は8枚のNVIDIA GeForce RTX4090を使います.

memorizationが発生していると判定するには, 人間が訓練データの画像と生成結果を見比べる, というのでもいいですが大変すぎるので何かしらの指標を用意します. ここではSSCDを使用します. 簡単に述べると,

• $\mathrm{SSCD}_{\mathrm{train}}$: プロンプト $c$ にから生成された画像 $\bold{x}_0$ と訓練画像 $\bold{x}$ の類似度
• $\mathrm{SSCD}_{\mathrm{generate}}$: 生成された画像同士の類似度の平均

の2つからなり, これの平均をとります.

$$\mathrm{SSCD}\ {\mathrm{score}}=\dfrac{\mathrm{SSCD}_{\mathrm{train}}+\mathrm{SSCD}_{\mathrm{generate}}}{2}$$

$\mathrm{SSCD}_{\mathrm{generate}}$ は多くの既存研究には登場しませんが, これを加えることで「訓練画像には似ていないけど, 生成画像がほぼ同一で多様性がない」場合を考慮します（いわゆるモード崩壊の事象. 拡散モデルではモード崩壊はあまりみられませんが, 全く起きないわけではありません）. スコアを出したので一定以上の値を超えたらmemorizationが発生していると判定できます. 今回は閾値を0.75とします. 既存研究では, この値を超えたものの90%はmemorizationであると報告されています.

Memorizationは単なる過学習ではない

まずは以下を実験的に確認します.

拡散モデルにおけるmemorizationは過学習だけでは説明できない. CFG用いると記憶が強くなる一方で, denoisingの初期段階おける訓練損失は逆説的に大きくなる.

一般に, memorizationとは訓練データへの過学習の結果として現れると考えられています. これは一般的な機械学習を考えるとある程度当たり前です.

例えば, Stable Diffusion 2-baseのリポジトリを見てみると

The model is trained from scratch 550k steps at resolution 256x256 on a subset of LAION-5B filtered for explicit pornographic material, using the LAION-NSFW classifier with punsafe=0.1 and an aesthetic score >= 4.5. Then it is further trained for 850k steps at resolution 512x512 on the same dataset on images with resolution >= 512x512.

と書かれています. これくらいの訓練規模で過学習が発生するのかどうかは議論の余地がありそうです. 部分的に出てくるとかではなく, 画像全体で人間が見ると全く同じレベルに過学習をしていることになります（同じ画像が何枚もデータセットにあればできそうですが）. この疑問を調べます.

memorizationが過学習を反映しているかを確かめるために, 訓練時には $g=1.0$ とします. すると, 損失関数は

$$\mathcal{L}=\|\dfrac{\sqrt{\overline{\alpha_t}}}{\sqrt{1-\overline{\alpha_t}}}(\hat{\bold{x}}_0^{(t)}-\bold{x})\|_2^2$$

です. ほぼ全ていつもの記号ですが, $\hat{\bold{x}}_0^{(t)}$ はtimestep $t$ における $\bold{x}$ の予測で

$$\hat{\bold{x}}_0^{(t)}=\dfrac{\bold{x}_t-\sqrt{1-\overline{\alpha_t}}\varepsilon_{\theta}(\bold{x}_t)}{\sqrt{\overline{\alpha_t}}}$$

です. 過学習が起きている場合, $\|\hat{\bold{x}}_0^{(t)}-\bold{x}\|_2^2\approx0$ です. 実際に結果を見てみます.

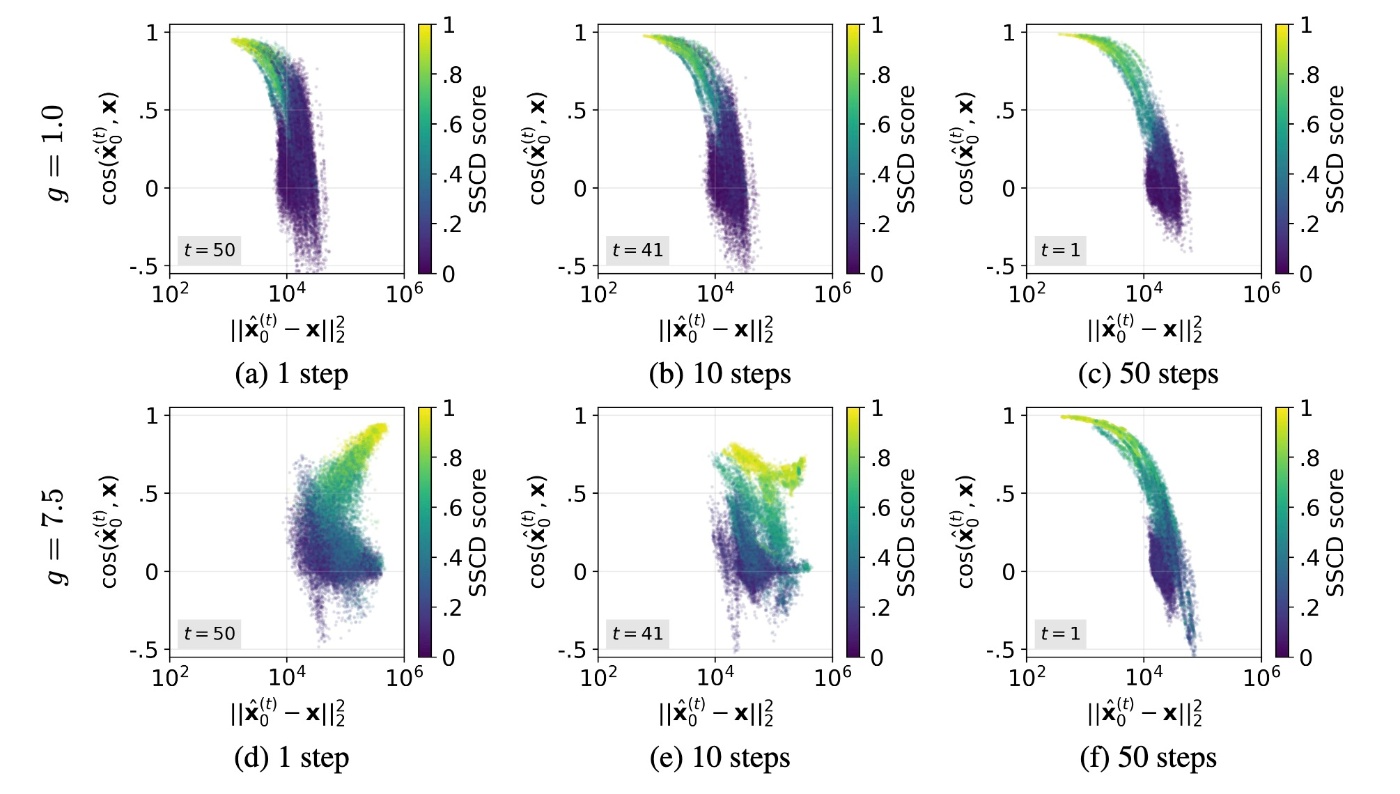
まず, 上段の(a-c)のCFGがない場合についてです. loss $\|\hat{\bold{x}}_0^{(t)}-\bold{x}\|_2^2$ は, 全てのタイムステップでmemorizationが生じている場合（黄色の部分）で一貫して小さくなっています. これは過学習の雰囲気がしています. 生成結果を見てみます.

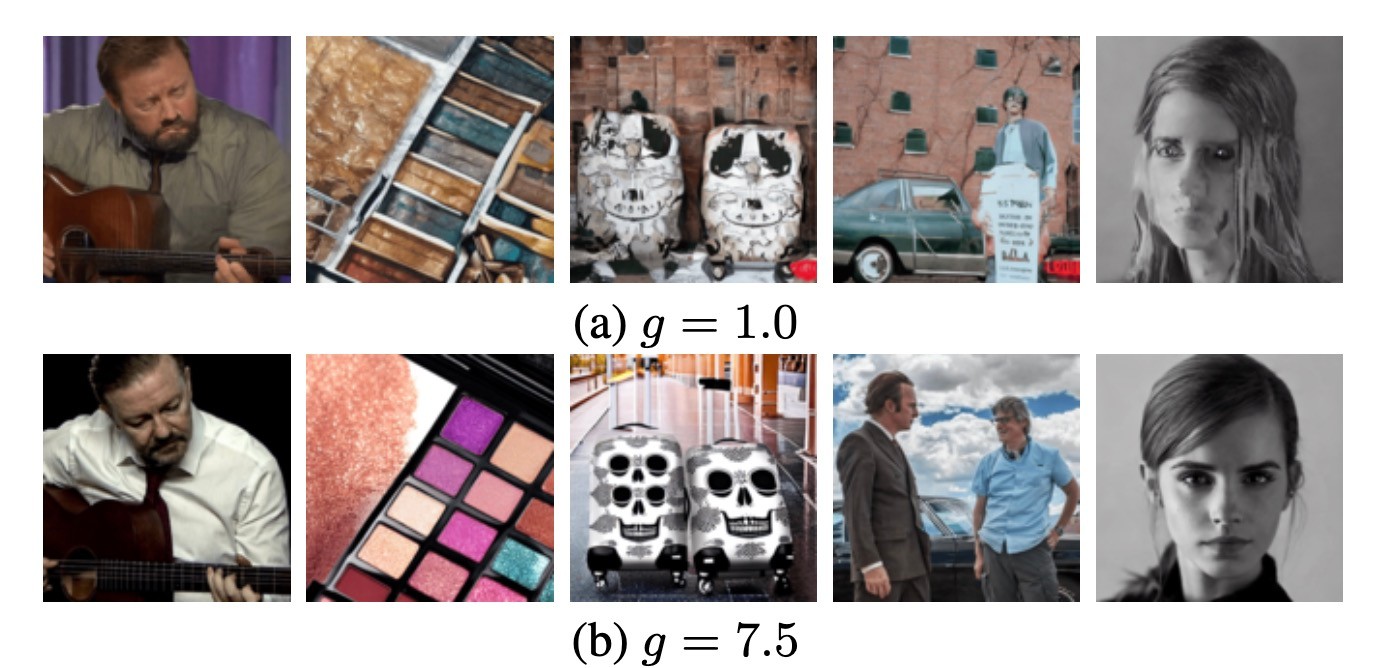
実際には, CFGがないと品質が大幅に劣化することがわかります.

では, 実際にCFGありの場合である下段(d-f)を見てみます. 先ほどと様子が異なります. memorizationが起きている場合でも, denoisingの初期段階ではlossが大きいことがわかります.

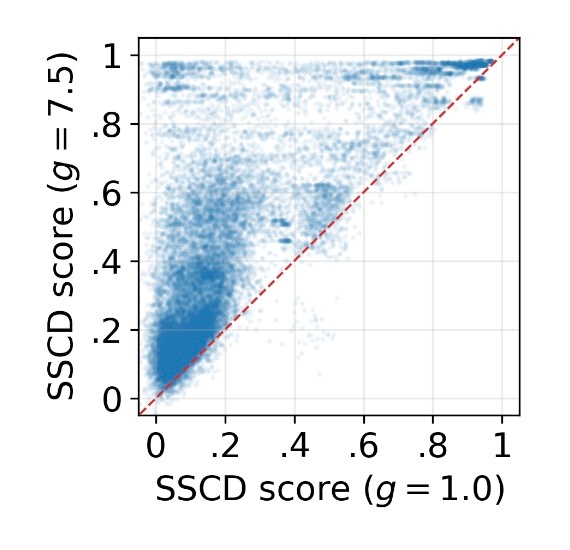
また, CFGありの方がなしの場合よりもSSCDが高くなっていることもわかります.

denoising初期段階での過大評価

先ほどの図 (a-f)では, $\hat{\bold{x}}_0^{(t)}$ と $\bold{x}$ のcosine類似度が $y$ 軸にプロットされています. memorizationが発生している状況では, CFGの有無に関わらず2つのベクトルはほぼ平行になります. これは $\hat{\bold{x}}_0^{(t)}\approx k\bold{x}$ と書けます. CFGがない場合は $k\approx1$ で, 経験的に $k>1$ です. そのため, CFGはdenoisingの初期段階において予測の大きさを増大させます. ベクトル的に考えれば方向は同じなのですが大きさが大きくなるため, $\bold{x}$ の過大評価につながります. これはCFG scale $g$ に起因します.

$$\hat{\bold{x}}_0^{(t)}=\dfrac{\bold{x}_t-\sqrt{1-\overline{\alpha}_t}\tilde{\varepsilon}(\bold{x}_t, \bold{e}_{\mathcal{c}})}{\sqrt{\overline{\alpha}_t}}$$

でした. また, $\tilde{\varepsilon}(\bold{x}_t, \bold{e}_{\mathcal{c}})=(1-g)\varepsilon(\bold{x}_t, \bold{e}_{\empty})+g\varepsilon(\bold{x}_t, \bold{e}_{\mathcal{c}})$ です. $t=T$ のとき, 以下の3つの特性が成り立ちます.

1. unconditionalおよびconditionalなノイズ予測の両方で, 初期の潜在変数 $\bold{x}_T$ と高いcosine類似度を示す.

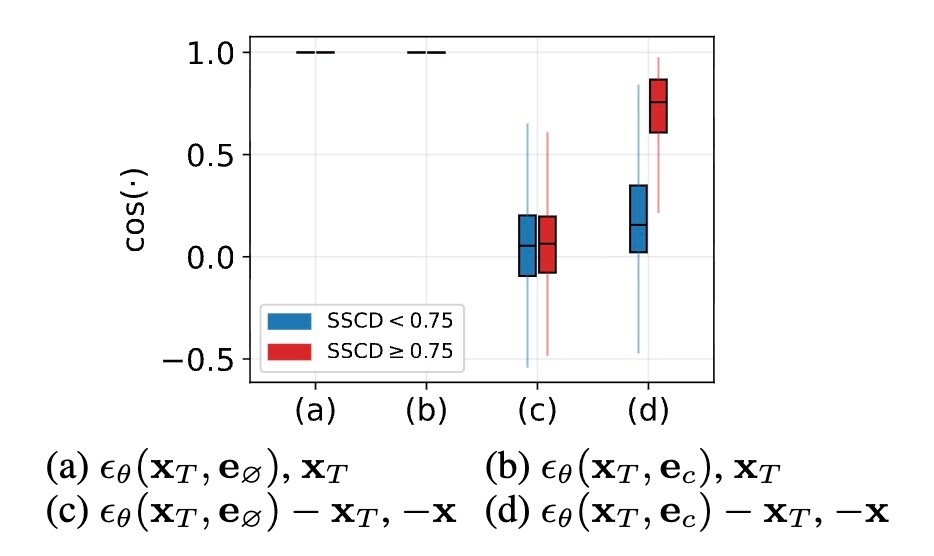
   $\varepsilon=\dfrac{\bold{x}_T-\sqrt{\overline{\alpha}_T}\bold{x}_T}{\sqrt{1-\overline{\alpha}_T}}$ で, $\overline{\alpha}_T\approx0$ なので, 十分に訓練されたニューラルネットワーク $\varepsilon_{\theta}$ は $\bold{x}_T$ を近似します. 実際にcosine類似度を計測してみると, 下図の(a, b)のようにほぼ1であることがわかります.

2. unconditionalのノイズ予測は $\bold{x}$ に関する情報を含まない.

   空文字列の埋め込み $\bold{e}_{\empty}$ とランダムにサンプリングした潜在変数 $\bold{x}_T\sim\mathcal{N}(\bold{0}, \bold{I})$ は訓練データである $\bold{x}$ の情報は含みません. これはある程度当然です. すなわち, これらから予測されたノイズ $\varepsilon(\bold{x}_T, \bold{e}_{\empty})$ は $\bold{x}_T$ に由来する情報は持っていますが, $\bold{x}$ に由来する情報は持っていないです (本来はここにはマイナス符号がつきますが, ここでは簡単のために省略しています). 先ほどの図(c)がそのことを示しており, $\varepsilon(\bold{x}_t, \bold{e}_{\empty})-\bold{x}_T$ と $-\bold{x}$ のcosine類似度はほぼ0であることがわかります. また, $\|\varepsilon(\bold{x}_t, \bold{e}_{\empty})-\bold{x}_T\|_2^2\approx0$ です. これは下図(a)から経験的にわかります. (b)はmemorizationを起こしている画像とそうでない画像についての比較ですが, どちらの場合も0に近いことがわかります.
   
   以上のことから, unconditionalのノイズ予測には $\bold{x}$ に関する情報はなさそうということがわかります.

3. conditionalなノイズ予測は対照的に, $\bold{x}$ に関する情報を豊富に含む.

   先ほど, memorizationが起きている場合は $\hat{\bold{x}}_0^{(t)}\approx k\bold{x}$ であるという話をしました. これは, $\tilde{\varepsilon}(\bold{x}_t, \bold{e}_{\mathcal{c}})$ が $\bold{x}$ に関する情報を持っていなければならないことを意味しています. 実際に, $\hat{\bold{x}}_0^{(T)}=\dfrac{\bold{x}_T-\sqrt{1-\overline{\alpha}_{T}}\tilde{\varepsilon}(\bold{x}_{T}, \bold{e}_{\mathcal{c}})}{\sqrt{\overline{\alpha}_{T}}}$ が $\bold{x}$ に非常に近いことが下図の生成例から確認することができます.
   
   2で確認したように, $\varepsilon(\bold{x}_{T}, \bold{e}_{\empty})$ は $\bold{x}$ に関する情報は持たないので, 訓練データの情報は $\varepsilon(\bold{x}_{T}, \bold{e}_{\mathcal{c}})$ によってもたらされます. 先ほどのグラフ（以下に再掲）の(d)では(c)とは異なり, $\bold{x}$ に関する情報を含んでいることがわかります. 特に, memorizationが起きている場合は非常にcosine類似度が高くなります.
   

1-3を統合すると2つのことが言えます. まず, 1と2から $\varepsilon(\bold{x}_{T}, \bold{e}_{\empty})\approx\bold{x}_T$ が言えます. 次に, 1と3から $\varepsilon(\bold{x}_T, \bold{e}_{\mathcal{c}})\approx\bold{x}-s\bold{x}_T$ であることが言えます. $s$ は適当なスカラー値ですが, $\epsilon=\dfrac{1}{\sqrt{1-\overline{\alpha}_T}}\bold{x}_T+\dfrac{\sqrt{\overline{\alpha}_T}}{\sqrt{1-\overline{\alpha}_T}}\bold{x}$ ですので, $s\approx\dfrac{\sqrt{\overline{\alpha}_T}}{\sqrt{1-\overline{\alpha}_T}}$ です. 従って

$$\tilde{\varepsilon}(\bold{x}_T, \bold{e}_{\mathcal{c}})\approx\bold{x}_T-g\dfrac{\sqrt{\overline{\alpha}_T}}{\sqrt{1-\overline{\alpha}_T}}\bold{x}$$

です. 以上から

$$\hat{\bold{x}}_0^{(T)}=\dfrac{\bold{x}_T-\sqrt{1-\overline{\alpha}_T}\tilde{\varepsilon}(\bold{x}_T, \bold{e}_{\mathcal{c}})}{\sqrt{\overline{\alpha}_T}}\approx g\bold{x}$$

です. したがって、CFG scale $g$ を増加させると, $\hat{\bold{x}}_0^{(T)}$ における $\bold{x}$ の寄与が線形に増幅され, これが直接的に過大評価と訓練損失の増大を引き起こすことがわかります.

このことを可視化したのが以下の図になります. 左から $g=0.5, 1, 2$ の場合です.

なぜ初期段階で過大評価が起きるのか

初期段階で過大評価になっていることはわかりました. これが起こる理由を考えてみます.

まず, $\varepsilon_{\theta}$ は中間的な潜在変数 $\bold{x}_t$ と, text embedding $\bold{e}_{\mathcal{c}}$ あるいは $\bold{e}_{\empty}$ を入力して $\bold{x}_t$ に含まれているノイズを予測しています. text embeddingは固定なので, 各タイムステップにおける予測結果は基本的に $\bold{x}_t$ に応じて決定されます. 下図は, 異なる $\bold{x}_T$ からdenoiseされた $\bold{x}_t$ の共分散行列のトレースをタイムステップごとにプロットしたものです. memorizationが発生している黄色の部分に着目すると, トレースが小さくなっており, $\bold{x}_t$ 間の多様性が低いことがわかります.

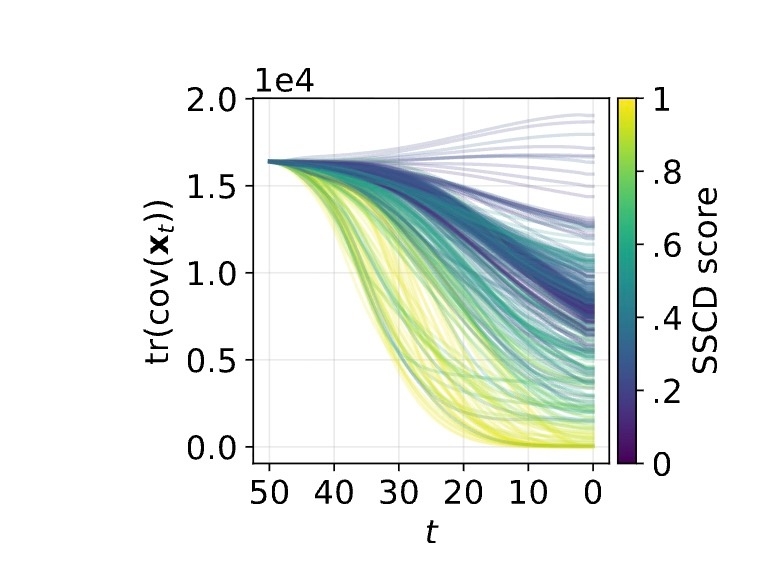
この多様性の低下は, 以前触れた過大評価によって, 各潜在変数 $\bold{x}_t$ が異なる実行においても同一情報 $\bold{x}$ の比率を大きく受け継ぐために発生します. その結果, memorizationが発生している状況では初期のタイムステップで予測結果が類似してしまい, denoisingの経路はほぼ同一となります.

上図もそのことを示します. $\Delta\bold{x}_{t-1}=\bold{x}_{t-1}-\bold{x}_t$ の第一主成分はmemorization時はdenoisingの初期段階で単一方向に強く整列しています.

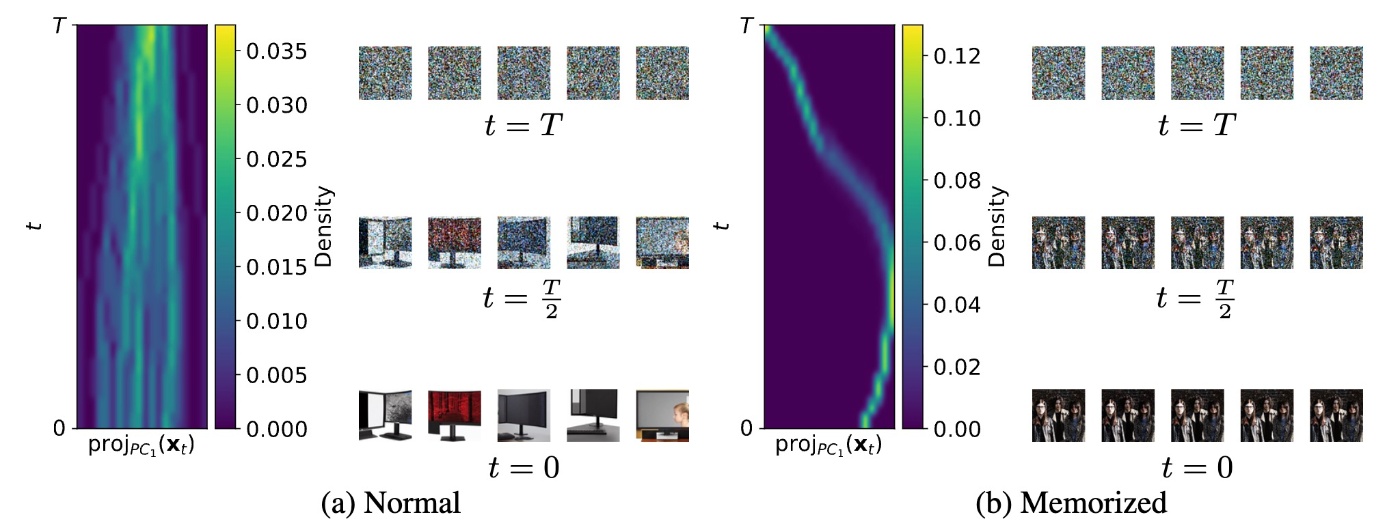
通常のプロンプトの場合, 下図(a)のように, $\bold{x}_T$ が異なることによって潜在変数が発散する (diverge)様子が確認できますが, memorizationが発生している場合は下図(b)のように経路がほぼ同一に収束します. つまり, 過大評価によって引き起こされる潜在変数の早期収束がmemorizationの主要因であると考えることができます. 特に, 初期段階と言っても $t=40$ の時点で2つ上の図で示したトレースとSSCDの相関が0.7を超えており, 高くなります.

この収束の様子をさらに詳しくみます. memorization時において $\bold{x}_t$ の分解手法を導入します. memorization発生時はlossが $\mathcal{L}\approx0$ です. すると $\epsilon\approx\varepsilon_{\theta}(\bold{x}_t, \bold{e}_{\mathcal{c}})$ です. このとき

$$\epsilon\approx\dfrac{\bold{x}_T-\sqrt{\overline{\alpha}_T}\bold{x}}{\sqrt{1-\overline{\alpha}_T}}\approx\varepsilon_{\theta}(\bold{x}_t, \bold{e}_{\mathcal{c}})$$

です. すなわち $\bold{x}\approx\hat{\bold{x}}_0^{(t)}\approx\dfrac{\bold{x}_t-\sqrt{\overline{\alpha}_t}\bold{\epsilon}}{\sqrt{1-\overline{\alpha}_t}}$ なので, 言い換えると

$$\bold{x}_t=\left(\sqrt{\overline{\alpha}_t}-\dfrac{\sqrt{\overline{\alpha}_T}}{\sqrt{1-\overline{\alpha}_T}}\right)\bold{x}+\dfrac{\sqrt{1-\overline{\alpha}_t}}{\sqrt{1-\overline{\alpha}_T}}\bold{x}_T$$

です. $\overline{\alpha}_T\approx0$ を用いて

$$\bold{x}_t=\sqrt{\overline{\alpha}_t}\bold{x}+\sqrt{1-\overline{\alpha}_t}\bold{x}_T$$

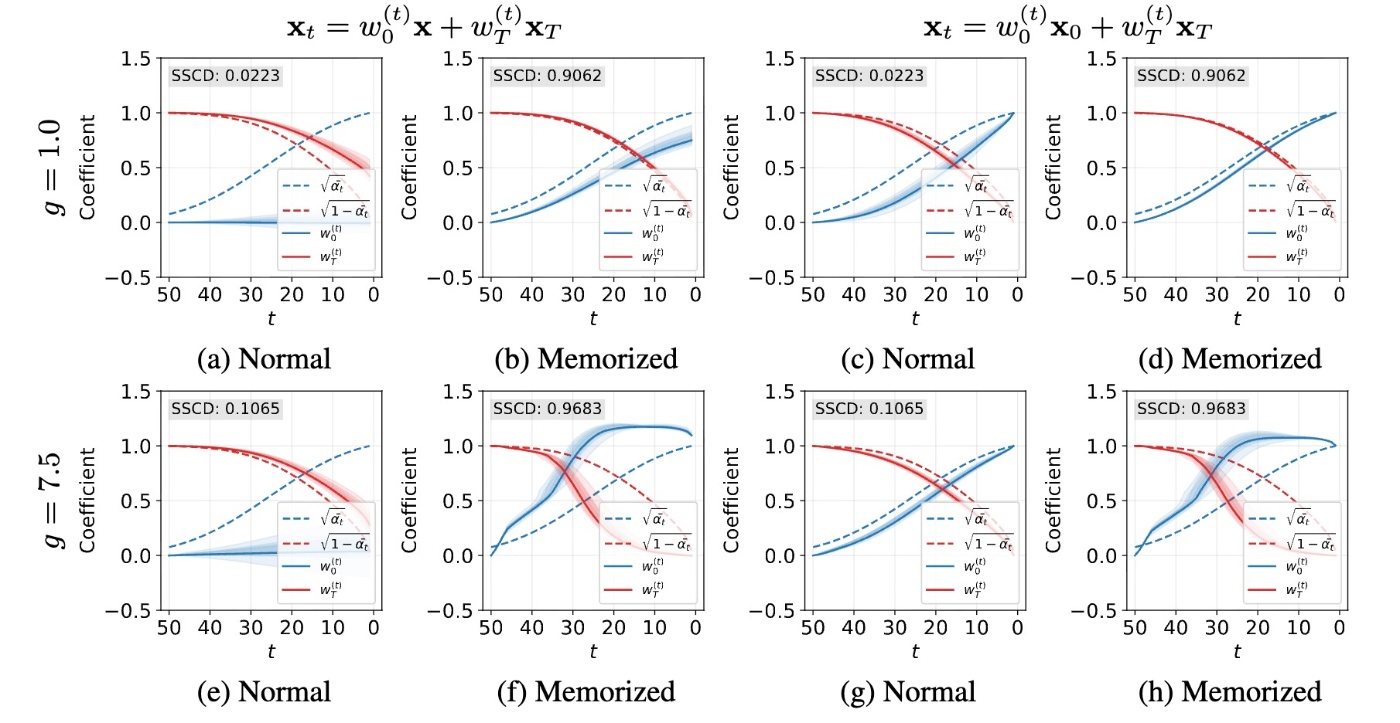
と分解できます. denoisingにおいて, 初期ノイズの項 $\bold{x}_T\sim\mathcal{N}(\bold{0}, \bold{I})$ を段階的に抑制しつつ, 潜在変数 $\bold{x}$ の寄与を増やしていくと見ることができます. $\bold{x}_t=w_0^{(t)}\bold{x}+w_T^{(t)}\bold{x}_T$ という最小二乗問題を解くことで上の式を検証できます. つまり, $w_0^{(t)}, w_T^{(t)}$ を $\sqrt{\overline{\alpha}_t}, \sqrt{1-\overline{\alpha}_t}$ とそれぞれ比較します. 結果は下図の左半分(a, b, e, f)に示されます.

結果をまとめると以下のようになります.

図(a, b)
CFGなしの場合 ($g=1.0$)では, memorization発生時, $w_0^{(t)}$ と $w_T^{(t)}$ はそれぞれ $\sqrt{\overline{\alpha}_t}$ と $\sqrt{1-\overline{\alpha}_t}$ をより忠実に追従していることがわかります(図b). これは $\bold{x}_t=\sqrt{\overline{\alpha}_t}\bold{x}+\sqrt{1-\overline{\alpha}_t}\bold{x}_T$ が過学習 ($\mathcal{L}\approx0$)に起因するmemorizationであることを仮定しているので, 予想通りと言えます. 通常の場合は図aのように $w_T^{(t)}$ 大まかに従いますが, $w_0^{(t)}$ はほぼ全てのタイムステップで0であることがわかります. これは生成結果が $\bold{x}$ とは似ておらず, 他の成分がdenoisingの過程で構築されていることを示唆しています.

図(e, f)
memorization発生時は, $g=7.5$ の状況下において, denoising初期における $\bold{x}$ の寄与が増幅されて (\hat{\bold{x}}_0^{(T)}\approx g\bold{x}), その結果として後続の潜在変数に過度に $\bold{x}$ の情報が注入されます. 言い換えると, $w_0^{(t)}$ は理論的なスケジュールである $\sqrt{\overline{\alpha}_t}$ よりも早く増加し, それに応じて $w_T^{(t)}$ は早く減少します. これは図(f)からも確認できます. 通常のプロンプトの場合は(e)と(a)からわかるように, CFGの有無に関わらず結果は同じような感じになっています.

図(c, d, g, h)
こちらは $\bold{x}$ が未知の場合です. $\bold{x}_0$ を訓練画像 $\bold{x}$ の代わりに用いた場合の結果です. 通常のプロンプト場合（図c, g）は理論的なスケジュール通りの変化をしています. これは図(a, b)でdenoisingの際に強化される成分が $\bold{x}_0$ で, denoisingの経路のゴールが早い段階で定まり, denoising中に徐々に増幅されていることを意味しています. memorizationが発生している場合はCFGがないときは理論的なスケジュールに一致し, あるときは $w_0^{(t)}$ が急速に増加して $w_T^{(t)}$ が急速に減少しています. これもdenoisingの初期段階で $\bold{x}$ が過大評価されていることを示しています.

SSCDとの結び付け

$\bold{x}_t$ の分解とSSCDを結び付けます. 各タイムステップで集めた以下の3つの量を計算します.

1. $\sum_{t=T}^{1}(\mathbb{E}[w_0^{(t)}]-\sqrt{\overline{\alpha}_t})$: memorizationされた画像 $\bold{x}$ の過剰な寄与を示します. この値が大きいほど $\bold{x}$ の過大評価を表します.
2. $\sum_{t=T}^{1}(\mathbb{E}[w_T^{(t)}]-\sqrt{1-\overline{\alpha}_t})$: 初期ノイズ $\bold{x}_T$ の早期抑制を示します. この値が大きいほど $\bold{x}_T$ の影響がスケジュールよりも早く消失し, $\bold{x}$ の影響が早く支配的になることを表します.
3. $\sum_{t=T}^{1}\{(\mathbb{E}[w_0^{(t)}]-\sqrt{\overline{\alpha}_t})-(\mathbb{E}[w_T^{(t)}]-\sqrt{1-\overline{\alpha}_t})\}$: 理論的なdenoisingの経路からの逸脱度合いを表します.

結果を散布図で見てみます.

簡単のため, $\sqrt{\overline{\alpha}_t}, \sqrt{1-\overline{\alpha}_t}$ は生成間で一定で比較には影響しないとします. 相関係数は高いです. 著者らは全て非常に高いとしていますが, (b)の0.7が非常に高いのかはやや疑問です. どちらにせよ, $\bold{x}$ の情報が早い段階で過剰に注入された結果, $\bold{x}_T$ の成分が多様性を確保するほど残らなくなるということがわかると思います.

思ったこと

• 論文を物語として見るならば, いいところで終わってしまった感じがあります. 読者としては「仕組みがわかったなら軽減できるよね？」くらいまで期待してしまうので. 査読には響くのかはよくわかりませんが...

参考文献

• Juyeop Kim, Songkuk Kim, and Jong-Seok Lee. How diffusion models memorize, 2025.
• https://huggingface.co/stabilityai/stable-diffusion-2-base
• Nicholas Carlini, Jamie Hayes, Milad Nasr, Matthew Jagielski, Vikash Sehwag, Florian Tram`er, Borja Balle, Daphne Ippolito, and Eric Wallace. Extracting training data from diffusion models. In Proceedings of the 32nd USENIX Conference on Security Symposium, SEC ’23, USA, 2023. USENIX Association.