Zenn
📌

Locating and Editing Factual Associations in GPT

2024/09/16に公開
機械学習
NLP
LLM
tech

今回はROMEの論文を細かく見ていきます. arXivの方を見ると, 第5版まで出ていますので, ここでは第5版を扱います. ことわりのない限り, 図表は全て元論文からの引用とします.

関連リンク

書籍情報

Meng, K., Bau, D., Andonian, A., and Belinkov, Y. Locating and editing factual associations in gpt. In Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., and Oh, A. (eds.), Advances in Neural Information Processing Systems, volume 35, pp. 17359–17372. Curran Associates, Inc., 2022.

はじめに

言語モデルはどこにその知識を格納しているのでしょう？この論文ではその点を扱います. 言語モデルは世界についての事実を推論することができます. 例えば, “The Space Needle is located in the city of,”と与えられたら, 正しい答えである"Seattle"を推論することが期待されますし, 実際にそうであると思われます. これは自己回帰のGPTだけでなくmasked BERTなどでも見られる現象です. ここではGPT-likeの自己回帰モデルに的を絞ってそのような知識がどこに蓄積されているのかを調査します. masked modelsでは研究が行われていますが, GPTのようなモデルはunidirectionalであるという点で異なります.

2つのアプローチを用いてこの目標を達成します. ひとつめはhidden state activationsのcasual effectsを追跡することです. これにはcausal mediation analysisを用います. これによって, あるsubjectに関する知識の想起を仲介するモジュールを特定することができます. 実験ではlast subject tokenを処理する際に, 中間層のFFN (feed-forward MLPs) が決定的な役割を果たしていることがわかります.

ふたつめはひとつめで得られた結果が正しいことを確認するためのテストとして, Rank-One Model Editing method (ROME)を提案します. これはFFNの挙動を決定するパラメータを代替する手法です. ROMEが標準的なzero-shotベンチマークで他のモデル編集手法と似たような効果を発揮することを確認することで, 事実がそこに蓄積されていることを保証します.

更なるROMEの評価として, より難しいケースを考えます. そのために反実仮想挿入データセット (dataset of counterfactual assertions)を導入します.

以降では, 大規模な学習済み自己回帰TransformerモデルをLLMと称します.

Interventions on Activations for Tracing Information Flow

LLMのパラメータのどこに事実があるのかを見つけるために, 著者らは個々の事実の推論時に最も強い因果効果を持つ特定の隠れ層を分析・特定することから始めました.　個々の事実をタプル t=(s, r, o) によって表します. s はsubject, o はobject, r は2つを繋ぐrelationです. LLMから事実を引き出すために, (s, r) について記述された自然言語プロンプト p を与え, o のモデルの推論結果を調査します.

語彙 V に対するLLM G: \mathcal{X}\rightarrow\mathcal{Y} はトークンの列 x=[x_1, \ldots, x_T]\in\mathcal{X} をx に続くような次のトークンの確率分布 y\in\mathcal{Y}\subset\mathbb{R}^{|V|} にマッピングします. Transformerでは, i 番目のトークンは, h_i^{(0)}=\mathrm{emb}(x_i)+\mathrm{pos}(i)\in\mathbb{R}^{H} から始まる隠れ状態ベクトル h_i^{(l)} に埋め込まれます. 最終的な出力 y=\mathrm{decode}(h_T^{(L)}) は最後の隠れ状態から読み込まれます.

そこで, G 内部の計算を隠れ状態 h_i^{(l)} のgridとして可視化します. 各層 l にglobal attention a_i^{(l)} とlocal MLP m_i^{(l)} を足します. 数式にすると

\begin{align*} h_i^{(l)}&=h_i^{(l-1)}+a_i^{(l)}+m_i^{(l)} \\ &\qquad a_i^{(l)}=\mathrm{attn}^{(l)}\left(h_1^{(l-1)}, h_2^{(l-2)}, \ldots, h_i^{(l-1)}\right) \\ &\qquad m_i^{(l)}=W_{proj}^{(l)}\sigma\left(W_{fc}^{(l)}\gamma\left(a_i^{(l)}+h_i^{(l-1)}\right)\right) \end{align*}

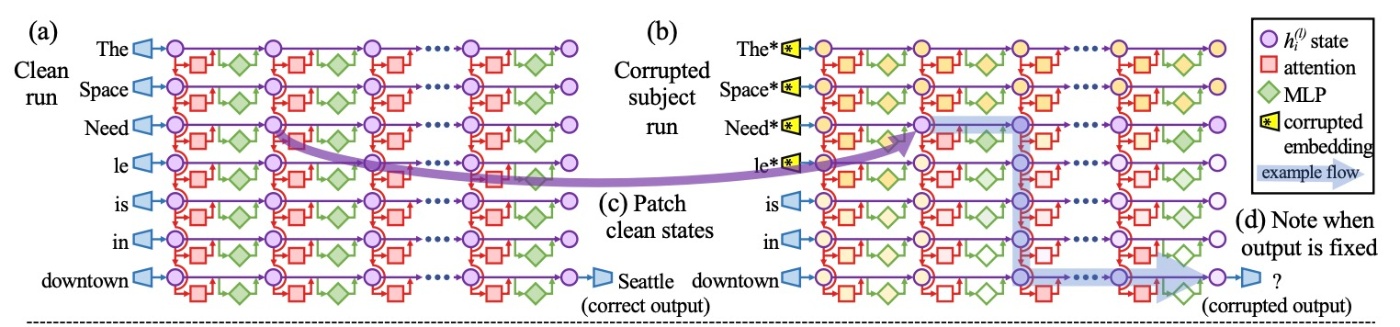
です. 各MLP層には2層からなるニューラルネットワークがあります. それらは W_{proj}^{(l)}, W_{fc}^{(l)} でパラメータ化されています. そして非線形の活性化関数である \sigma　(ReLU) と非線形の正規化層である \gamma を持ちます. 図にすると以下の図の(a)のようになります.

Causal Tracing of Factual Associations

上図の状態のgridはcausal graphを形成しています. このグラフは左側の入力から右下の出力までの様々なpathを持っています.

先行研究によると, これは因果媒介分析の自然な場合です. 各状態の事実の推論に対する寄与を計算するために, 全ての G 内部の活性化を3つの実験で観察します.

  • clean run: 事実の推論
  • corrupted run: 推論が傷つけられたもの
  • corrupted-with-restoration run: 1つの状態を回復した場合の推論能力のテスト

より詳しく見ていきます.

clean runでは, factual prompt x を G に渡して全ての隠れ活性化 \{h_i^{(l)}|i\in[1, T], l\in[1, L]\} を集めます. 先ほどの図の(a)と同じ状況です. ここでは o=\mathrm{"Seattle"} が出力として期待されます.

corrupted runでは, ネットワーク G が実行される前にsubjectが難読化 (obfuscated) されます. 具体的には, x が埋め込み [h_1^{(0)}, h_2^{(0)}, \ldots, h_T^{(0)}] として埋め込まれた後, 直ちにsubject entityに対応する全ての添字 i に対して h_i^{(0)}\coloneqq h_i^{(0)}+\varepsilon とします. ここで, \varepsilon\sim\mathcal{N}(0;\mu) です. \mu は埋め込みの標準偏差の3倍の値を用います. その後, G を通常通り実行します. すると, 破壊された活性化 \{h_{i*}^{(l)}|i\in[1, T], l\in[1, L]\} が得られます. G がsubjectに関する情報を一部欠落して受け取るので, 誤った出力が期待されます. 上図の(b)がその概要となります.

corrupted-with-restoration runでは, corrupted runと同じように G はノイズ入りの埋め込みに対して計算を行います. 先ほどと異なる点として, トークン \hat{i} と層 \hat{l} を除いてその計算を行うことです. そこで, G をhookして, G がclean state h_{\hat{i}}^{(l)} を出力するようにします. 以降では介入を行わずに計算を行います. 直感的には, 難読化されたsubjectによって他の多くの状態が破壊されているにもかかわらず, 正しい事実を回復するためのclean stateの能力は, 計算グラフにおいて因果的な重要性を示すと考えることができます.

以上が3つの実験です. 以降ではその実験においてどのように結果を評価するかを見ます.

まず, \mathbb{P}[o], \mathbb{P}_*[o], \mathbb{P}_{*, \mathrm{clean} h_i^{(l)}}[o] をそれぞれclean, corrupted, corrupted-with-restoration runにおいて o を排出する確率を表すとします. これらは入力 x に依存しますが, 簡単のために省略します. total effect (TE) は \mathrm{TE}=\mathbb{P}[o]-\mathbb{P}_*[o] で定義します. indirect effect (IE) は 特定の媒介状態 h_i^{(l)} に対して \mathrm{IE}=\mathbb{P}_{*, \mathrm{clean} h_i^{(l)}}[o]-\mathbb{P}_*[o] で定義します. これらを全てのstatementに対して平均をとって, 各状態に対する average total effect (ATE) と average indirect effect (AIE) を取得します.

Causal Tracing Results

ここではCausal Tracingの結果を確認します. 媒介させるものをさまざまに変化させながら, 1000を超えるfactual statementに対してAIEを計算します. 1.5BのモデルであるGPT2-XLを用いた結果が以下のようになっています. ATEは18.6%で, 効果の大部分がlast subject tokenにおいて, 強く因果的な個別状態 (レイヤー15でAIE=8.7％) によって媒介されていることに注意が必要です. 推論直前のlate siteに強い因果状態が存在することはあまり驚きはありませんが, last subject tokenのearly siteにこれが出現することは新しい発見です.

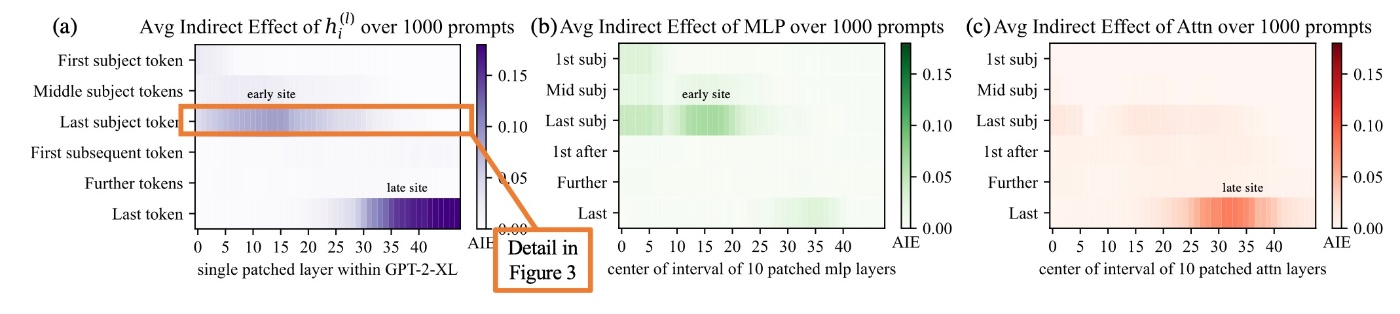
MLPとattentionの寄与の因果効果を分解すると, 上図 (b, c) と下図 (f, g) からearly siteの決定的な役割が示唆されます. last subject tokenでのMLPのAIEは6.6%ですが, attentionは1.6%です. attentionはlast tokenでより重要であることがわかります.

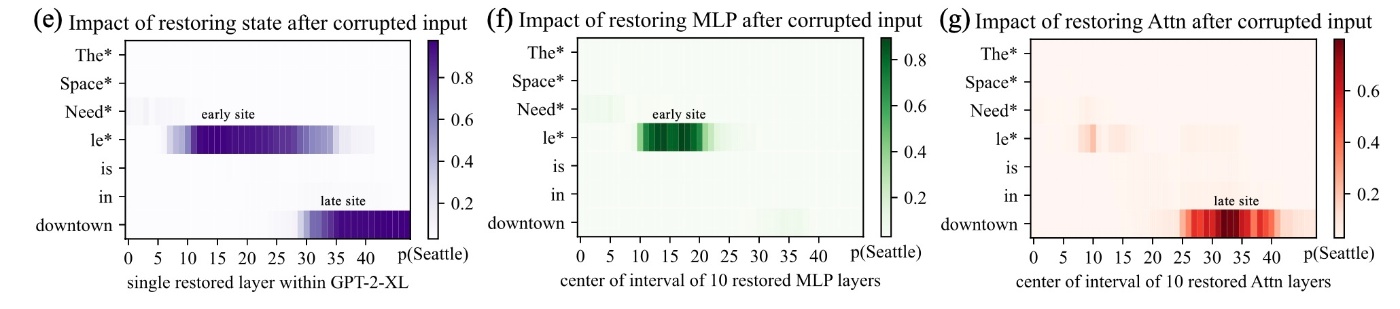
最後に, early siteにおけるMLPの特別な役割を明確にするために, IEを修正したcausal graphを用いて分析します.

上図には (a)-(f) までラベルが付与されていますので, 順番に見ていきます.

まず, 各MLPモジュールの寄与をcorrupted runによって集めます (a). 次に, 因果効果を測定する際にMLPの効果を分離するために, トークン i におけるMLP計算を切断し, h_i^{(l)} のclean stateの挿入による影響を受けないようにするために, corrupted stateをfreezeするよう計算グラフを修正します (b).

さて, 修正されたグラフoriginalのグラフのAIEを比較します (c). まず最初の層ですが, その後のMLPの活動なしでは自身の因果効果を失っています (d). それとは対照的に, 後ろの層になると状態の効果はMLPの活動に影響されにくくなっています. attentionを切り離すとこのような変化は見られません (f). この結果は事実の想起において中間層のMLPが必要不可欠であることを示しています (e).

このことから著者らは局所化されたMLPのkey-value mappingがsubjectに関する事実を想起させると仮説を立てました.

The Localized Factual Association Hypothesis

著者らはcausal tracingの結果に基づいて, 事実の関連付けを蓄積するための特定のメカニズムを提唱しています. 具体的には, 中間層のMLPモジュールがsubjectをエンコードする入力を受け取り, そのsubjectに関する記憶された特性を想起させる出力を生成します.　中間層のMLPは蓄積された情報を出力し, 集められた情報が後ろの層のattentionによってlast subject tokenにコピーされるというものです.

この仮説は, 知識の関連付けについて3つの次元に沿って, 特定の位置に局所化します.

  1. MLPモジュール
  2. 特定の中間層
  3. last subject tokenの処理時

この仮説は先行研究と一致するものです.
(先行研究では「MLP層が知識を保存する」という考えや, 「self attentionが情報をコピーする役割を果たす」という考えです.)

さらに, 「Transformer層の順序を変更しても挙動にはほとんど影響がない」という先行研究の発見に基づいて, 著者らはこの仮説が完全なものであることを提案しています. つまり, 中間層の個々の層の選択や配置には特別な役割がないということで, どの事実も中間層のMLPのいずれかに等しく保村されていると推測できます. この仮説を検証するために特定の中間層のMLPモジュール l^* に注目し, その重みを明示的に変更することで任意の事実が保存できるかどうかを確かめます.

Interventions on Weights for Understanding Factual Association Storage

MLPが事実の関連付けの想起の役割を担っていそうなことはすでに確認した通りです. では, 事実はどのように重みに保存されているのでしょう. 先行研究では, FFNの2つあるMLPがkey-valueメモリとして機能していることがわかっています. 最初の層である W_{fc}^{(l)} のニューロンがkeyを形成し, 2番目の層である W_{proj}^{(l)} のニューロンが関連するvalueを取得するといった具合です. しかし, 著者らの仮説はMLPが線形連想メモリとしてモデル化できるというもので, 先行研究の個々のニューロンに基づくものとは異なります.

この仮説の検証のために, Rank-One Model Editing (ROME) を用いて事実の関連付けを修正するという介入を行います. 現在のタプル t^c=(s, r, o^c) を新しいタプル t^*=(s, r, o^*) に置き換えることができ, その際に一般化と特異性の両方を実現できれば, 仮説がしめされます.

Rank-One Model Editing: Viewing the Transformer MLP as an Associative Memory

ここでは, W_{proj}^{(l)} を線形連想メモリとしてみます. 任意の線形操作 W がベクトルのkeyの集合 K=[k_1|k_2|\ldots] とそれに対応するベクトルのvalueの集合 V=[v_1|v_2|\ldots] のためのkey-value storeとして機能できると観察されます. この操作は WK\approx V を解くことで行われます. その二乗誤差はMoore-Penrose pseudoinverse W=VK^+ を用いて最小化されます. 先行研究では, 新しいkey-valueのペア (k_*, v_*) をメモリに最適に挿入することは制約付き最小二乗問題を解くことで達成できるとしています. これは畳み込みネットワークで解決していましたが, 全結合においては以下の閉形式で解を求めることができます.

\mathrm{minimize}\ \|\hat{W}K-V\|\quad \mathrm{s.t.}\ \hat{W}k_*=v_*\quad \mathrm{by\ setting}\ \hat{W}=W+\Lambda(C^{-1}k_*)^\top

ここで, W は元の行列を, C = KKT はWikipedia textのサンプルから推定されたkey k の非中心共分散をキャッシュすることで得られる定数です. また, \Lambda = \frac{(v_* − Wk_*)}{(C^{-1}k_*)^\top k_*} は新しいkey-valueのペアが元のメモリ行列に与える残差誤差に比例するベクトルです. この単純な代数構造により, 一度 (k_*, v_*) を計算すれば任意の事実を直接挿入することがかのうです. あとは適切な k_* と v_* を選ぶだけです.

ここで, ROMEの概要図を示します.

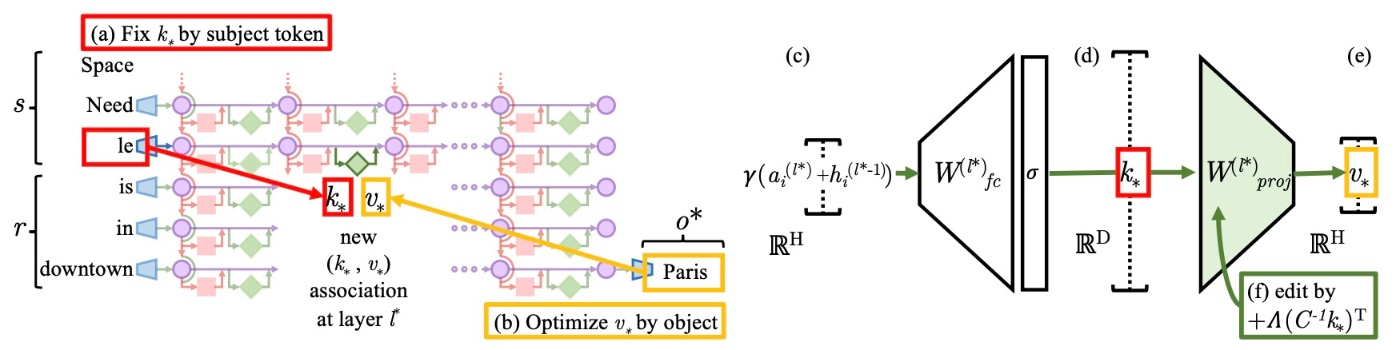
ROMEは残り3ステップから構成されます. 順番に見ていきます.

Step 1: subjectを選択するための k_* の選定

MLPの入力がfinal subject tokenで果たす決定的な役割に基づいて, last tokenでのsubjectを表す入力をlookup key k_* として選びます. 具体的には, 活性化を収集することで k_* を計算します. subject s を含むテキスト x を G に私, 特定の層 l^* とlast subject token の添字 i で, MLP内の非線形関数後の値を読み取ります (上図のdの部分です). 状態は, テキスト内で s に先行するトークンに依存して変化するので, subject s で終了するテキストの小さな集合に対して平均をとって k_* を決めます. 実用上は x_j を50のランダムトークン列として生成します. この生成には G を用い, トークン列の長さは2〜10とします.

k_*=\dfrac{1}{N}\sum_{j=1}^Nk(x_j+s),\quad\mathrm{where}\ k(x)=\sigma\left(W_{fc}^{(l^*)}\gamma\left(a_{[x],i}^{(l^*)}+h_{[x], i}^{(l^*-1)}\right)\right)

Step 2: 事実想起のための v_* の選択

次に, 新しい関係 (r, o^*) を s の特性としてエンコードするベクトル v_* を選びます. v_*=\argmin_{z}\mathcal{L}(z) で得られます. 目的関数 \mathcal{L}(z) は

\dfrac{1}{N}\sum_{j=1}^{N}\underbrace{-\log \mathbb{P}_{G(m_i^{(l^*)}\coloneqq z)}[o^*\mid x_j+p]}_{\mathrm{Maxmimizing}\ o^*\ \mathrm{probability}}+\underbrace{D_{KL}\left(\mathbb{P}_{G(m_{i'}^{(l^*)}\coloneqq z)}[x\mid p']\|\mathbb{P}_G[x\mid p']\right)}_{\mathrm{Controlling\ essence\ drift}}

です. 最初の項はベクトル z を求めようとしており, それをsubjectの最後のトークン i での MLP の出力として代入すると, ネットワークが事実のプロンプト p に対して目標オブジェクト o^* を予測するようになります. 第2項はプロンプト p' ("{subject} is a"の形式) の予測に対する未変更のモデルとのKL Divergenceを最小化を行います. これによって, モデルがsubjectの本質を理解する能力を維持します. ここで, モデルのパラメータは変更されていない点に注意が必要です. ここではあくまで v_* を求めることが目標です. k_* 同様, v_* でもランダムなプロンプトを用いて平均を取ります.

Step 3: 事実の挿入

完全な事実 (s, r, o^*) を表すためのペア (k_*, v_*) を計算したら,

\mathrm{minimize}\ \|\hat{W}K-V\|\quad \mathrm{s.t.}\ \hat{W}k_*=v_*\quad \mathrm{by\ setting}\ \hat{W}=W+\Lambda(C^{-1}k_*)^\top

を適用してMLPの重み W_{proj}^{(l^*)} をランク1の更新で事実挿入をします.

Evaluating ROME: Zero-Shot Relation Extraction (zsRE)

ROMEの性能を確認します. 比較対象は直接最適化を行うものか新しいネットワークを導入するものです. 具体的には

  • Fine-Tuning (FT): 1つの層に対してAdamをearly stoppingありで用い, -\log\mathbb{P}[o^*\mid x] を最小化する手法
  • Constrained Fine-Tuning (FT+L): FTに加えてパラメータ空間の L_{\infty} normを加えます.
  • Knowledge Editor (KE)とMENDはどちらもhypernetworksを用いる手法です

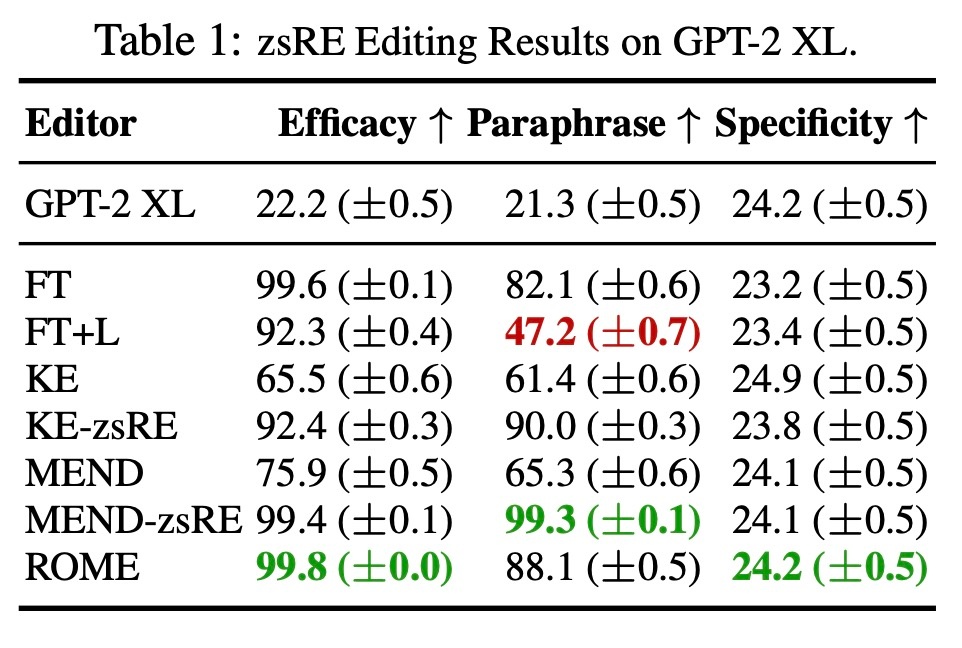
まずは, Zero-Shot Relation Extraction (zeRE) で実験を行います. 10000件のレコードを用います. 各レコードには1つのfactual statement, その言い換え, おっよび無関係な事実が含まれています. 評価指標はEfficacy, Paraphrase, Specificityです. EfficacyとParaphraseはそれぞれfactual statementとその言い換えにおける編集後のモデルの精度 \mathbb{I}[o^*=\argmax_{o}\mathbb{P}_{G'}[o]] を, Specificityは編集後のモデルの無関係な事実に対する精度を測定します. 結果を見てみます.

ROMEは他の手法と比較しても遜色ない結果を得ることができています. これは手法の複雑さを加味すると優位に立てそうな結果だと著者らは述べています. 特に, ROMEがモデルに再現されるような関連付けの挿入は難しくないことがわかります. 言い換えに対する頑健性は高いですが, zsRE分布に特化して訓練しているKE-zsREやMEND-zsREには及びません. また, zsREにおけるSpecificityはモデルの無関係な事実への影響度合いを敏感に測定することができていない指標であることがわかります.　これは, promptは多数の可能な事実なサンプリングされているからです. 直感的に, ある知識を編集すると最も影響が及ぶのはそれに関連した知識です. そのため, 正しく影響を測るには関連する近隣のsubjectで行う必要があると著者らは考えています.

Evaluating ROME: Our CounterFact Dataset

先ほど見た評価指標は, ROMEをある程度評価できるもので, 評価のスタートとしては妥当ですが, 事実に関する意味のある変更に対する深い修正と, 表面的な言葉の変更を区別するための詳細な洞察は提供されないです.

著者らは特に, 重要な変更の有効性を測定したいです. 先行研究では, 標準的なモデル編集ベンチマークが, モデルが以前に高得点をつけた提案のみを測定するので, 難易度を過小評価していることを指摘しています. そのため, 著者らはより難易度の高い誤った事実 (s, r, o^*) の集合を作成しました. これは正しい事実 (s, r, o^c) に比べて低いスコアで始まります. Efficacy Score (ES) は, 編集後に \mathbb{P}[o^*]>\mathbb{P}[o^c] となったデータの割合を示します. また, Efficacy Magnitude (EM) は, \mathbb{P}[o^*]-\mathbb{P}[o^c] の平均値です. 一般化の測定のため, 各反事実に対して (s, r) と同等の言い換えたpromptの集合を構築し, ES, EMと同様に計算されたParaphrase Scores (PS), PMを報告します. 特異性を測定するために, (s_n, r, o^c) が真である近隣のsubject s_n の集合を構築します. これらのsubjectをを変更しないように, \mathbb{P}[o^*]>\mathbb{P}[o^c] を測定し, 成功率をNeighborhood Score (NS), 差をNMとして報告します. 一般化と特異性のトレードオフを測定するためにES, PS, NSの調和平均をScore (S) として報告します.

また, 著者らは生成されたテキストの意味的一貫性も測定したいと考えています. そのため, sで始まるテキストを生成し, 対象の属性 o^* を共有するsubjectに関する参照テキストと比較します. 比較にはunigram TF-IDFベクトルのcos類似度を使用します (RS). 最後に, 生成されたテキストの流暢さの低下を確認するために, -\sum_k f(k)\log_2f(k) で与えられるbi-gramおよびtri-gramのエントロピーの加重平均を計算します. ここで, f(\cdot) はn-gramの頻度分布で, GEとして報告します. この量は生成されたテキストが反復的である場合に低下します.

これまで述べた指標の測定を簡単に行うため, CounterFactという, 言語モデルにおける反事実的な編集を評価するための挑戦的な評価データセットを導入します. このデータセットは全部で21919件のレコードがあり, さまざまなsubject, relation, および言語的なバリエーションが豊富にあります. CounterFactの目標は, 新しい事実の堅牢な保存と, ターゲットワードの表面的な再現を区別することです. 以下の表はその構成の概要を示しています.

Confirming the Importance of Decisive States Identified by Causal Tracing

Causal Tracingを用いた実験では, 決定的な隠れ状態が特定されました. これらの状態を出力するMLPモジュールに事実の関連が実際に保存されていることを確認するために, 様々な層やトークンをターゲットとしてROMEを適用した際の効果を調べます.

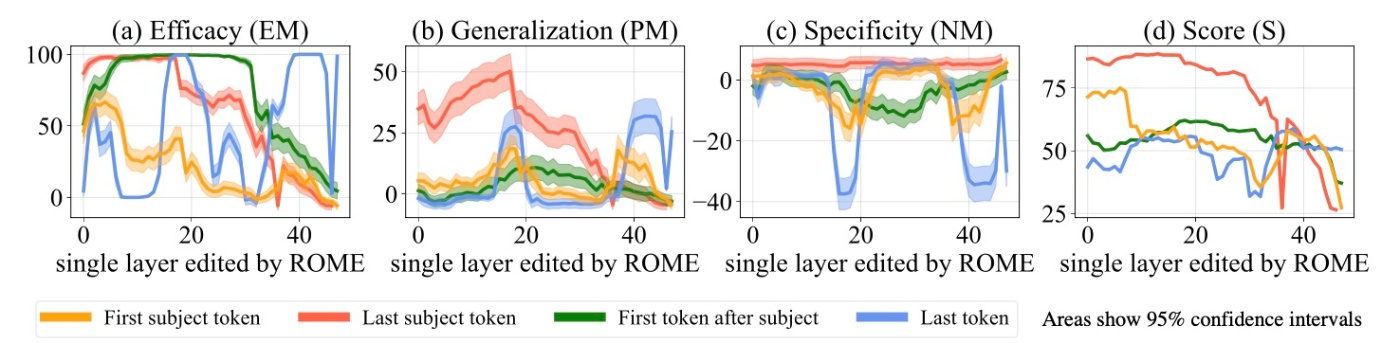
この図は一般化 (a, b, d)と特異性 (c)の両方を評価する4指標をプロットしたものです. 因果効果との強い相関が確認でき, 書き換えはlast subject tokenで最も成功し, 特異性と一般化の両方が中間層でピークに達しています. より前のトークンや後のトークンをターゲットとすると, 一般化や特異性が低下することもわかります. さらに, 編集が最も一般化されるのはCausal Tracingで特定された初期サイトの中間レイヤーに対応しており, 18番目の層です. これらの結果は事実の関連がどこに保存されているのかだけでなく, どのように保存されているのかについても正確に理解していることを示唆しています.

以下の表では, GPT2-XL (1.5B) とGPT-J (6B)における定量的結果を示します. この実験では, 以前の実験で用いたベースラインに加えて, ニューロンの解釈可能性に基づく方法であるKnowledge Neurons (KN) とも比較を行います. KNは, まず勾配に基づく寄与によって知識に関連するニューロンを選択し, その後対応する行のMLPの重みをスケーリングされた埋め込みベクトルを追加して修正します.

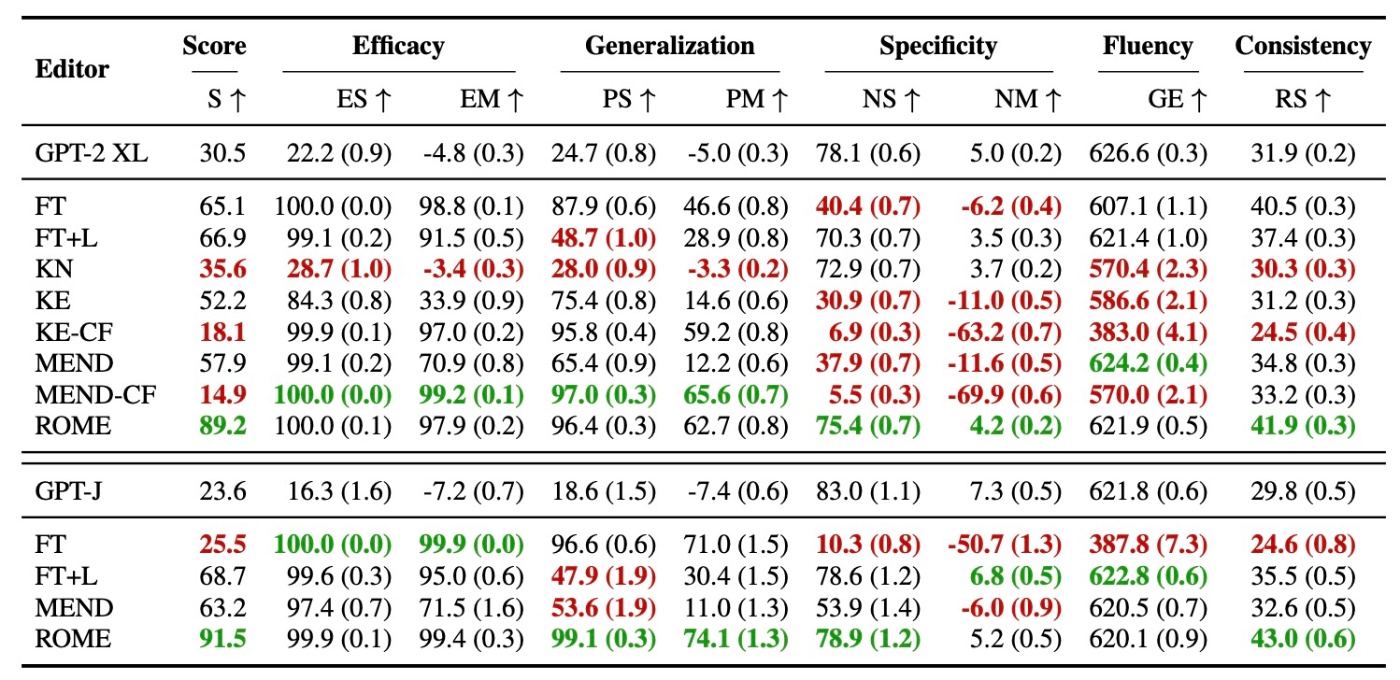
結果を見ると, ROME以外の全ての方法が以下のいずれか, または両方の問題を示すことがわかります.

  1. 反事実的な文にoverfittingし, 一般化に失敗する
  2. underfittingしてしまい, 無関係なsubjectにたいしても同じ新しい出力を予測する

例えばFTは高い一般化を達成しますが, 近隣のentitiyに対して誤りを起こします (2に該当). 逆に, FT+Lは1に該当します. KEやMENDは両方に当てはまり, 高い効果があるにも関わらず一般化や一貫性などが劣っているために再生が示唆されます. KNは効果的な編集を行うことすらできません. ROMEは今回の比較の中では一般化と特異性の両方において高い性能を示します.

Comparing Generation Results

生成結果をひとつだけ確認してみます. この例では, "Pierre Curie’s area of work is medicine" という反事実的な編集をGPT2-XLに行ったものです (実際にはPierre Curieは物理学者です).

一般化の観点から見てみます. すると, FTとROMEは言い換えに対しても対応できていて, 異なる言い回しでも物理学者ではなく医学者としてPierre Curieを説明しています. 一方で, FT+L, KE, MENDは一般化に失敗しており, 言い回しによっては医学または物理学のどちらかを交互に使っています. (c, d, e1またはc1, e, d1). KEは流暢さに問題があり (d), medicineを繰り返し生成しています.

特異性の観点から見ます. FT, KE, MENDは特異性に問題があり, 無関係な人物の職業も変更しています. 例えば編集前はRobert Millikanを天文学者として生成していたGPT2-XLが編集後はFT+Lでは生物学者 (b1), KEとMENDでは医学者 (d2, e2)と生成しています. これに対してROMEでは特異性を保持しており, 天文学者として生成しています.

おわりに

この論文では1.5BのGPT2-XLを用いています. 今から見ると非常に小規模なモデルですが, これより大きい規模のモデルが当時は非公開だったことが大きいです. この論文がarXivに投稿されたのが2022年2月で, 176BのオープンアクセスなモデルであるBLOOMがarXivに投稿されたのは同年11月ですので, まだ大規模化は進んでいないときと考えられます. 最近ではモデルの規模が大きくなると性能が突然上がるようなこと (創発性)が言われてたりします[1]. このことを踏まえると, より大きいモデルでも同じ傾向なのかを確認したくなります. 例えば以下の記事では6Bのモデルを用いて類似の結果を得ることができています. 軽く調べただけなので6B程度ですが, おそらく13Bなどでも同様なのではと思います.

https://zenn.dev/ohtaman/articles/llm_finetune_lora

また, ROMEはその分析手法を見て分かるように, SVO形式を前提としています. 当然ですが, SVO以外で終わる形式の文章も存在します. そのような形式に対する研究では軽く調べた感じだと日本語論文で

https://www.anlp.jp/proceedings/annual_meeting/2024/pdf_dir/P10-27.pdf

などがあります.

参考文献

  • Meng, K., Bau, D., Andonian, A., and Belinkov, Y. Locating and editing factual associations in gpt. In Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., and Oh, A. (eds.), Advances in Neural Information Processing Systems, volume 35, pp. 17359–17372. Curran Associates, Inc., 2022.
脚注

  1. これは評価指標によるものだと主張する論文もあります ↩︎

Discussion