Text-to-Imageのメカニズムを細かく見る【論文】

Towards Understanding the Working Mechanism of Text-to-Image Diffusion Model

この論文では, Stable Diffusionのメカニズムがどうなっているかを探求します. LDMのような話は前提なのでしません. もう少し踏み込んで, 生成時にどのようになっているかを分析・考察しています.

貢献は以下の3つです.

1. stable diffusionのdenoising processにおいて全体的な形状とディテールはそれぞれ最初の方と最後の方の段階で再構成される.
2. text promptは[EOS]トークンの影響がdenoising processの初期段階では支配的で, テキスト情報を伝える役割を果たす. また, モデルはディテールを埋める際には自身の生成画像に依存する.
3. 観察結果をうまく適用して25%以上の高速化を達成.

それぞれを順番に見ます.

First Overall Shape then Details

まず, 分析に入る前にベースとなっている2つの文献の一部分を紹介します. 1つめはNVIDIAのeDiff-Iです. この論文以下の画像の例を用いて, 2つのpromptをどのタイミングで変化させると生成画像が変化するかを確認しています. prompt1からprompt2に変化させるとき, denoising processの終盤で変えても生成画像に大きな変化はありません (30%では顔などに変化がありますが, 構図などの大まかな部分の変化はないです). 逆に, 序盤で変化させると見るからに生成例が変化していることがわかります. このことから生成された画像の全体的な形状は, denoising processの最終段階で変更することが困難であると言えます.

2つめはRafael C. GonzalezのDigital Image Processingです (デジタル画像処理の教科書ならなんでもいいように思えます)^[1]. 画像処理をやってる人にとっては常識の話ですが, 画像の低周波成分は全体的な形状, 高周波成分は細部の情報を表しています. これは大局的な情報は変化が少ないために低周波成分に対応し, 局所的な部分では急激に変化するために高周波成分に対応するというだけの話です.

以上から, denoisingの初期段階と最終段階で, それぞれ低周波成分と高周波成分を復元していることを理論的および経験的に検証します. すると, First Overall Shape then Detailsを説明できます.

Two Stages of Denoising Process

まず実験設定として, T2I-compbenchと同様に, "a {attribute} {noun}"という形のpromptを1600用意します. attributeには色とテクスチャを表す形容詞を入れます. その比率は半分なので, 色が800でテクスチャが800のpromptが出来上がります. その後, T2I-compbenchからさらに別のpromptを1000用意します. これらのpromptでPromptSetを構成します. 今回用いたものでは, nounが230種類, 色が33種類, テクスチャが23種類です. 画像生成はStable Diffusion1.5をDDIM 50stepsで行います.

生成結果を見てみます. (a)では各トークン, 各時刻のcross attention mapが示されています. $t=40$ はdenoising processの序盤ですが, 非常に意味のある形状が確認できます. ここから, 視覚的にFirst Overallであることがわかります. さらなる調査として, PromptSetに対して各トークンのcross attention mapの平均を計算します. cross attention mapの形状と最終的な生成画像をCanny imageに変換して比較します. そこから各時刻においてF1 Score ($\mathrm{F1}_t$)を計算します. 下図の(b)では相対F1 Score ($\mathrm{F1}_{t}/\mathrm{F1}_{1}$)がプロットされています. この結果は, cross attention mapの形状がdenoising processの最初の段階で生成画像に急速に近づいていることを表しています.

以上の結果は先ほどの考察と以下の論文の結果と一致しています.

https://arxiv.org/abs/2404.02747v1

ちなみにこの論文では触れられていませんが, Prompt-to-Promptでも同じようなことが言われています.

https://arxiv.org/abs/2208.01626

Frequency Analysis

先ほどの現象をさらに説明するために周波数成分を解析します. 低周波成分は全体的な特徴を, 高周波成分は細かい部分の特徴を表すので, First Overall Shape then Detailsを説明するなら周波数の話をしないといけないというのが著者らの主張です.

以降はやや数学的な話をします. clean dataである $\boldsymbol{x}_0$ は各チャネルにつき $M\times N$ 次元とします. $\boldsymbol{x}_t$ はforward processにおけるノイズ付加と同じ操作で得ます. すなわち

$$\boldsymbol{x}_t=\sqrt{\overline{\alpha}_t}\boldsymbol{x}_0+\sqrt{1-\overline{\alpha}_t}\boldsymbol{\varepsilon}_t$$

です. $\boldsymbol{x}_t$ のフーリエ変換 $F_{\boldsymbol{x}_t}(u, v)$ は

$$\begin{align*} F_{\boldsymbol{x}_t}(u, v)&=\dfrac{1}{MN}\sum_{k=0}^{M-1}\sum_{l=0}^{N-1}\boldsymbol{x}_{t}^{kl}\exp\left(-2\pi i\left(\dfrac{ku}{M}+\dfrac{lv}{N}\right)\right) \\[5pt] &=\sqrt{\overline{\alpha}_t}F_{\boldsymbol{x}_0}(u, v)+\sqrt{1-\overline{\alpha}_t}F_{\boldsymbol{\varepsilon}_t}(u, v) \end{align*}$$

です. $\boldsymbol{x}_0$ の分布はわからないので, 以降では $F_{\boldsymbol{\varepsilon}_t}(u, v)$ を探索します. ここで, 以下の補題が成り立ちます.

任意の $u\in[M],\ v\in[N]$ に対して, 少なくとも $1-\delta$ の確率で以下が成り立ちます.

$$\|F_{\boldsymbol{\varepsilon}_t}(u, v)\|^2\leq\dfrac{1}{\sqrt{MN}}\left(1+\sqrt{8\log\dfrac{2MN}{\delta}}\right)$$

証明はあとでみるとして今は一旦この事実を認めます. この式は画像サイズが大きいときに, 標準ガウス分布の周波数成分の強度がほぼ0になることを意味しています ($M, N\to\infty$ で右辺は0に収束します). よって, ノイズの付与されたデータ $\boldsymbol{x}_t$ の中の $\boldsymbol{x}_0$ の周波数成分はフーリエ変換の式から主に $\overline{\alpha}_t$ によって劣化することがわかります.

しかし, 以下の図で確認できるように, 画像の高周波成分とは対照的に低周波成分はロバストです. 例えば $t=20$ では時計の形状が低周波成分では確認できます.

証明

$\boldsymbol{\varepsilon}_{t}^{kl} (\mathrm{以後}\boldsymbol{\varepsilon}^{kl})$ をi.i.d.なガウシアン確率変数とします. 各 $k, l$ について

$$F_{\boldsymbol{\varepsilon}}(u, v)=\dfrac{1}{MN}\sum_{k=0}^{M-1}\sum_{l=0}^{N-1}\boldsymbol{\varepsilon}^{kl}\exp\left(-2\pi i\left(\dfrac{ku}{M}+\dfrac{lv}{N}\right)\right)=\dfrac{1}{MN}\sum_{k=0}^{M-1}\sum_{l=0}^{N-1}\boldsymbol{\varepsilon}^{kl}\exp(-i\theta_{uv}^{kl})$$

です. $\theta_{uv}^{kl}$ は $kl$ 番目の複素数の偏角で, 以後は簡単のために $\theta^{kl}$ を用います. 次に, この命題がガウス分布の集中不等式の直接の結果であることを示します. まず, 一次元フーリエ変換において, 次元 $M$ の下で証明し, これを二次元に拡張します.

複素数のノルムの定義から, 任意の特定の $u$ に対して

$$\|F_{\boldsymbol{\varepsilon}}(u)\|^2=F_{\boldsymbol{\varepsilon}}(u)\overline{F_{\boldsymbol{\varepsilon}}(u)}=\dfrac{1}{M^2}\boldsymbol{\varepsilon}^\top\Lambda\boldsymbol{1}\boldsymbol{1}^\top\overline{\Lambda}\boldsymbol{\varepsilon}$$

です. ここで, $\Lambda=\mathrm{diag}(e^{-i\theta^0}, \ldots, e^{-i\theta^{M-1}})$ です. さらに, $\boldsymbol{P}$ を $\boldsymbol{P}=(\sqrt{1/M}\boldsymbol{1}^\top, \ldots, )^\top\overline{\Lambda}$ とします. ここで, $(\sqrt{1/M}\boldsymbol{1}^\top, \ldots, )^\top$ はベクトル $\sqrt{1/M}\boldsymbol{1}$ とその直交補空間によって構成されます. $\boldsymbol{P}$ が直交行列であることがわかります. 次に, $\boldsymbol{y}=\boldsymbol{P\varepsilon}$ とすると $\boldsymbol{y}$ と $\boldsymbol{\varepsilon}$ は同じ分布を持ちますので,

$$\dfrac{1}{M^2}\boldsymbol{\varepsilon}^\top\Lambda\boldsymbol{1}\boldsymbol{1}^\top\overline{\Lambda}\boldsymbol{\varepsilon}=\dfrac{1}{M^2}\boldsymbol{y}^\top\boldsymbol{P}\Lambda\boldsymbol{1}\boldsymbol{1}^\top\overline{\Lambda}\overline{\boldsymbol{P}}^\top\overline{\boldsymbol{y}}=\dfrac{1}{M}\boldsymbol{e}_1^\top\boldsymbol{y}\overline{\boldsymbol{y}}^\top\boldsymbol{e}_1=\dfrac{1}{M}(\boldsymbol{y}^1)^2$$

$\boldsymbol{y}^1$ は標準正規分布に従います. Berstein’s inequalityをsub-exponential random　variable、すなわち $\chi_1^2$ に適用すると

$$\mathbb{P}(|F_{\boldsymbol{\varepsilon}}(u)-\mathbb{E}[F_{\boldsymbol{\varepsilon}}(u)]|\geq\delta)=\mathbb{P}\left(|(\boldsymbol{y}^1)^2-\mathbb{E}[(\boldsymbol{y}^1)^2]|\geq\delta\right)\leq2\exp\left(-\dfrac{1}{8}\min\{\delta^2,\delta\}\right)$$

$\delta\in(0, 1)$ なので確率 $1-\delta/M$ で

$$\dfrac{1}{M}-\dfrac{1}{M}\sqrt{8\log\dfrac{2M}{\delta}}\leq\|F_{\boldsymbol{\varepsilon}_t}(u)\|^2\leq\dfrac{1}{M}+\dfrac{1}{M}\sqrt{8\log\dfrac{2M}{\delta}}$$

となります.

この事実を潜在変数にも拡張できるとすると, First Overall Shape then Detailsを説明できます. 低周波成分はノイズ付加のプロセスの終わりまで劣化されないために, denoising processの序盤で回復されることになります.

このことを調査するために, PromptSetで生成した画像の低周波成分と高周波成分の変動をプロットしたものが下図です.

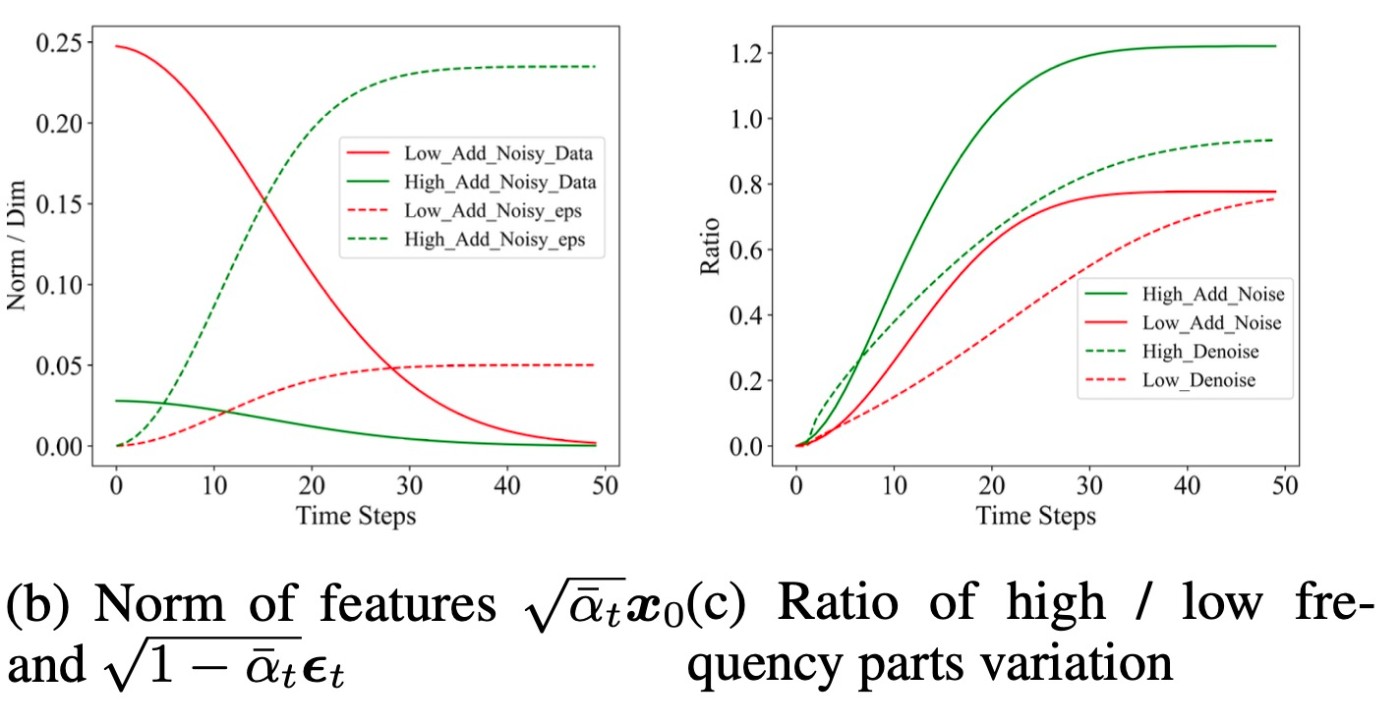
図の(b)における"Low_Add_Noisy_Data/eps"は $\sqrt{\overline{\alpha}_t}\boldsymbol{x}_{0}^{\mathrm{low}}$, $\sqrt{1-\overline{\alpha}_t}\boldsymbol{\varepsilon}_{t}^{\mathrm{low}}$ のノルムを表します. また, "High_..."はlowをhighに変えたものです. 図の(c)ではノイズ付加/除去プロセス中の画像の高周波/低周波成分の変動比を測定しています. 例えば"High_Add_Noise"は $\|\boldsymbol{x}_{t}^{\mathrm{high}}-\boldsymbol{x}_{0}^{\mathrm{high}}\|/\|\boldsymbol{x}_{0}^{\mathrm{high}}\|$ です. ここで, $\boldsymbol{x}_{t}^{\mathrm{low}}$ は低周波成分, $\boldsymbol{x}_{t}^{\mathrm{high}}$ は高周波成分です.

さて, 図の(c)では, 同一プロセスの中で $\boldsymbol{x}_t$ の挙動が類似しており, 低周波成分の再構築が高周波成分より速いことがわかります. 一方で, 図(b)の実線を見ると, 高周波成分のノルムが低周波成分のものより著しく低いことがわかります. これは自然画像由来の特性と考えられますが, 一方でガウシアンノイズについては逆の関係が言えます. 先ほどの命題から $\boldsymbol{\varepsilon}_t$ は0に近く, 高周波成分が80％のスペクトルを含むので $\boldsymbol{\varepsilon}_{t}^{\mathrm{high}}$ は $\boldsymbol{\varepsilon}_{t}^{\mathrm{low}}$ より大きくなります.

これらの観察結果は, First Overall Shape then Detailsを説明しています. 低周波成分はノイズ付加プロセスの終わりまで完全には破壊されないので, 逆方向のdenoising processではまずこれらが回復されます. 一方で高周波成分にはこの現象は当てはまりません. ノイズ付加プロセス中の速い段階で破壊されるため, denoisingの終わりまで回復しません.

The Working Mechanism of Text Prompt

denoising processではFirst Overall Shape then Detailsという2つの段階があることを確認しました. 次に, これらの段階におけるtext promptの役割を探ります. 主な観察結果は2つです.

1. 特殊トークン [EOS] がtext promptの影響を支配している
2. text promptは主にdenoising processの最初の全体の形の再構築段階で機能している

順番に見ていきます.

[EOS] Contains More Information

T2I Diffusion Modelsにおいて, text promptは主にCLIP Text Encoderでエンコーディングされます (Imagen以降, 巨大なモデルではT5-XXLが使われたりT5とCLIPを併用したりしますがここではそれらは考えないことにします). semantic token (SEM)は特殊トークン[SOS]および[EOS]に囲まれています. これらの3種類のトークンについて, cross attentionモジュールを介して情報が伝達されるので, まずは各クラスのcross attention mapにおけるピクセルに対する平均重みを計算します. 重みはPromptSet全体の平均を取っています.

これを見ると, [SOS]の重みが他のクラスと大差をつけて大きいことがわかります. CLIPはARモデルなので, [SOS]自体には意味的な情報がありません. このことから[SOS]の影響は主に他のcross attention map全体の調整であると考えられます. このことはLLMでも観察されている事象です. この論文で挙げられている例として以下の研究があります.

https://openreview.net/forum?id=NG7sS51zVF

いわゆるattentionのゴミ箱に近い話かなと思います. これについては以下の動画が参考になります.

https://www.youtube.com/watch?v=N-0eFoQYkrs

text promptの情報はSEMと[EOS]によって伝達されるので以降はこれらに焦点を当てます. SEMと[EOS]の両方がtext promptの意味情報を含んでいるため, まずどちらがT2I生成に大きな影響を与えるかを調べます.

PromptSetからtext promptのペアを3000組選びます (2000組はテンプレートに従い、残りの1000組は複雑なprompt)。各ペアで、2つのtext promptは"$[\texttt{SOS}] + \mathrm{Prompt}\ A (B) + [\texttt{EOS}]_{A(B)}$"として表現されます. 各ペアについて[EOS]を交換して新しいtext promptペアを"$[\texttt{SOS}] + \mathrm{Prompt}\ A (B) + [\texttt{EOS}]_{B(A)}$"として構築します.

これらのtext prompt (Switched-PromptSet, S-PromptSet)に基づいて生成された画像を調べます. 例えば $[\texttt{SOS}] + \mathrm{Prompt}\ A + [\texttt{EOS}]_B$ の場合はPrompt $A$ の $A$ を"souce", $[\texttt{EOS}]_B$ の $B$ を"target"と呼びます. これらのプロンプトに基づいて生成された画像についてそれぞれのsouce promptとtarget promptの一致度をおく呈します. これはCLIP Score, BLIP-VQA, MiniGPT4-CoTでスコアとします.

結果を確認します.

これによってsorce promptよりtarget promptの方がスコアがいい, すなわち生成画像はよりtarget promptに一致していることがわかります. これは, 無意味なSEMが付加されていても[EOS]に含まれる情報がdenoising processにおいて支配的であることを表します. 実際に, 生成例で確認します.

例えば上段の右2つは, [EOS]がswitchされています. すると, 生成された画像は[EOS]の内容に従っていることがわかります. Prompt $A+ [\texttt{EOS}]_B$ で生成された画像はPrompt $B$ の内容を反映していますし, Prompt $B+ [\texttt{EOS}]_A$ で生成された画像はPrompt $A$ の内容を反映しています. 下段も同様です.

このことから, T2IではSEMよりも[EPS]の方が大きな影響力を持つと考えることができます. この現象について, 著者らは2つの仮説を立てています.

1. 自己回帰的にエンコードされたtext promptのおかげで, 意味トークンとは異なり, [EOS]は完全なテキスト情報が含まれており, 生成された画像のパターンを決定する
2. promptには長さ76の制限があるため, [EOS]の数が通常, 意味トークンよりも多い

Appendix Cのでこの仮説が検証されていますが, ここでは省略します.

ここまでのことをまとめると, T2I生成では特殊トークンである[EOS]は生成される画像の全体的な情報 (特に形状)を決定すると言えます.

The Text Prompt Mainly Working on the First Stage

さて, これまでFirst Overall Shape then Detailsがdenoising processの特徴であるということがわかっています. そこで, ここではFirst Overall Shape then Detailsとtext promptの関係性について調べます.

S-PromptSetのpromptを使用したT2I生成の全50stepsのdenoising process中に, [EOS]の置き換えの開始点を変えます. 具体的には, 使用されるtext promptは"$[\texttt{SOS}] + \mathrm{Prompt} A + [\texttt{EOS}]_B (\mathrm{or\ }[\texttt{EOS}]_A)$"で, $t\in[\mathrm{Start\ Step}, 50] (\mathrm{or\ }t\in[0, \mathrm{Start\ Step}])$ です. 図にすると以下のようになります.

先ほどと同様に, source/targetのalignmentのスコアを計測します.

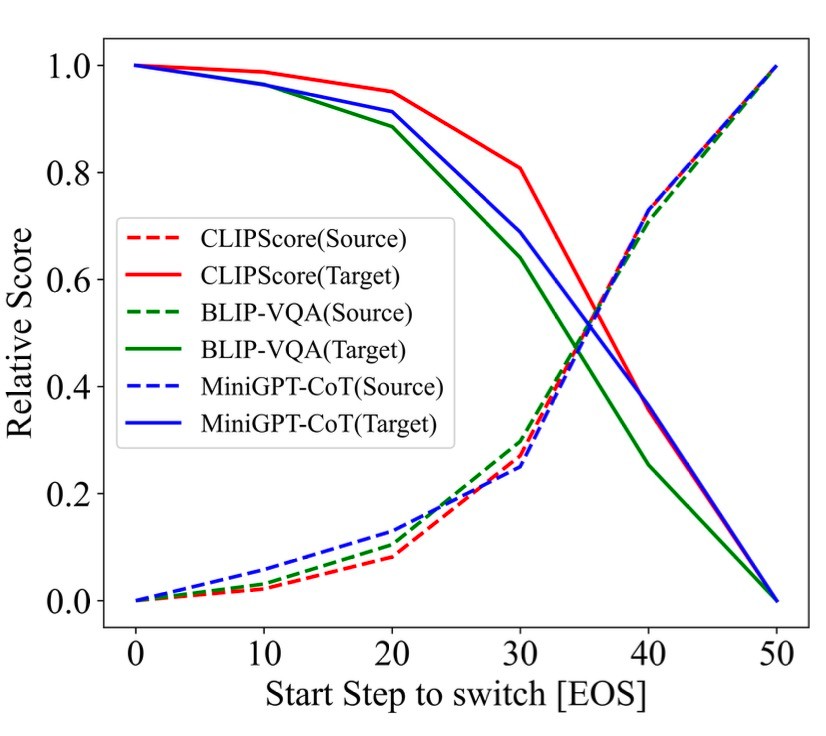
この図において, target promptとの整合性は, switchする $t$ が50に近づくと減少します. これは[EOS]の情報がdenoising processの最初の段階で伝えられていることを示しています.

続いて, text prompt全体でも同じことが言えるかを確認します. もし言えるなら, T2Iは小さい $t$ に対するdenoiseの結果のみに依存することになります. これを確認するためにはclssifier-free guidanceのguidance scaleを最初は0に, 途中から7.5にする設定で生成を行います. 図にすると以下のようになります.

PromptSetで実験した結果を示します. 比較対象は通常の生成です. 用いる指標はCLIPScoreとL1 distanceです. 結果は相対値 (最大-最小)によって報告されます. 結果を確認します.

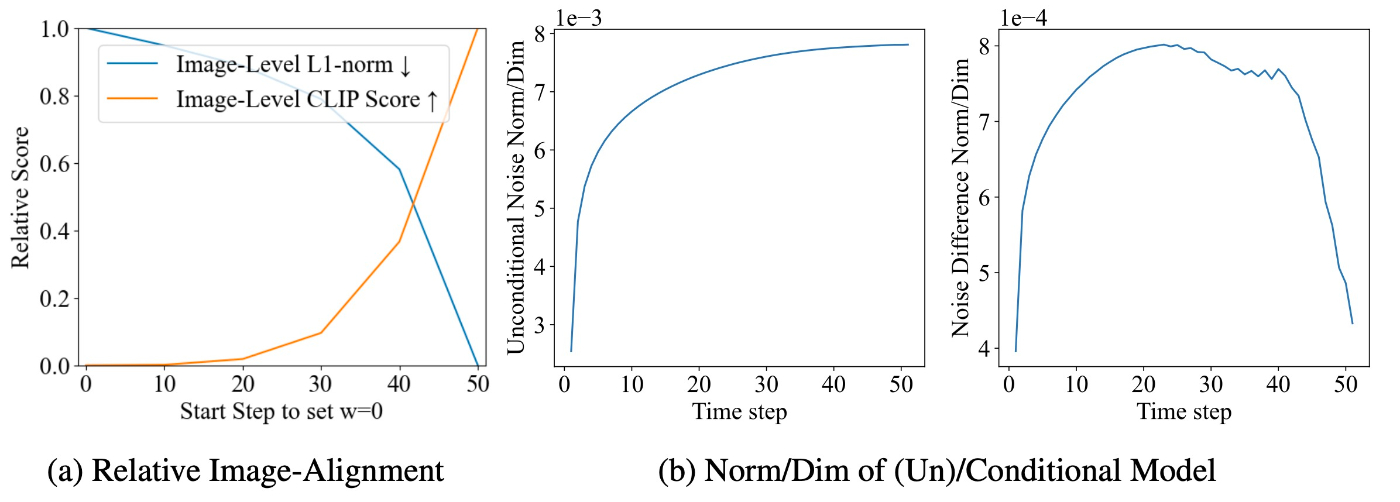
まず, (a)を見ます. 生成中, 時刻 $t\in[a, 50]$ ではテキスト情報が存在しません. (a)のグラフからは $a=30$ あたりから大幅に整合性が小さくなっていることがわかります. これは, denoising processの序盤でテキスト情報を消すと, その影響が生成した画像にはないことを示しています. すなわち, text promptの情報はdenoising processの初期段階で伝えられるということができます.

このことを少し数式の面から見てみます. 推論時は以下の式で生成を行なっています.

$$\begin{align*} \boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \mathcal{C}, \emptyset)=\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \emptyset)+w(\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \mathcal{C})-\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \emptyset)) \end{align*}$$

$\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \mathcal{C}, \emptyset)$ は, 技術的には $\nabla_{\boldsymbol{x}}\log p_t(\boldsymbol{x}_t\mid\mathcal{C})/\sqrt{1-\overline{\alpha}}$ を近似します. $p_t$ は $\boldsymbol{x}$ の密度です. そのときには以下の式で分解します.

$$\nabla_{\boldsymbol{x}}\log p_t(\boldsymbol{x}_t\mid\mathcal{C})=\nabla_{\boldsymbol{x}}\log p_t(\boldsymbol{x}_t)+\nabla_{\boldsymbol{x}}\log p_t(\mathcal{C}\mid\boldsymbol{x}_t)$$

この2式を比べると, $\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \emptyset)\propto\log p_t(\boldsymbol{x}_t)$ および $w(\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \mathcal{C})-\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \emptyset))\propto\log p_t(\mathcal{C}\mid\boldsymbol{x}_t)$ です.

SDEの論文によると, denoising processは対数尤度 $\log p_0(\boldsymbol{x}_0\mid\mathcal{C})$ を最大化することがゴールです.

次に, $\nabla_{\boldsymbol{x}}\log p_t(\mathcal{C}\mid\boldsymbol{x}_t)$ の方向に沿って移動する (すなわち $\log p_t(\mathcal{C}\mid\boldsymbol{x}_t)$ が大きくなる)ことは, $t$ の現象に伴ってtext prompt $\mathcal{C}$ と一致するように $\boldsymbol{x}_t$ を推し進めていることに相当します. これは非常に標準的な条件付き生成の手法です. 先ほどの図の(b)を見ます.

これに示されているように, denoising processの間に $\boldsymbol{x}_t$ は徐々に $\mathcal{C}$ と一致するようになります. これに伴って $\nabla_{\boldsymbol{x}}\log p_t(\mathcal{C}\mid\boldsymbol{x}_t)$ は小さくなります. その後, この項によって伝達される text promptの影響が $t\to0$ とともに減少します. First Overall Shape then Detailsがありますので, $\boldsymbol{x}_t$ は急速に $\mathcal{C}$ と一致します. これによって $\nabla_{\boldsymbol{x}}\log p_t(\mathcal{C}\mid\boldsymbol{x}_t)$ は急激に減少します.

Application

さて, これまで分析をしたので効率良い生成ができそうな気がします. 逆に, 効率良い生成ができないと分析結果の正当性を保証できません.

text promptの情報は主に $\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \mathcal{C})$ によって伝達されます. なので, denoising processの最初の数ステップの後にこの計算はやらなくてもよさそうな雰囲気があります. これはdenoising processの最初にテキスト情報がほぼ反映されているためです. すなわち, denoising processを以下のように変更できます.

$$\begin{align*} \boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \mathcal{C}, \emptyset)= \begin{cases} \boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \emptyset)+w(\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \mathcal{C})-\boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \emptyset)) & a\leq t \\ \boldsymbol{\varepsilon}_{\theta}(t, \boldsymbol{x}_t, \emptyset) & 0\leq t<a \end{cases} \end{align*}$$

図にすると以下の感じです.

評価を行います. DDIMとDPM-Solverを用いてMSCOCOの生成を行います. 使用するモデルはStable Diffusion 1.5, 2.1, Pixart-Alphaです. 生成時に $a$ を様々に変化させ, L1 distanceとImage-Level CLIP Score, FIDなどで比較します.

結果は, $a$ を適切な値に設定することでベースラインである通常の生成と同等の結果を得ることが確認できます. 例えば, $a=20$ のSD 1.5 (DDIM)は, 30%ほど計算コストを削減しつつ, $a=0$ のベースラインと同等です.

結果は定性的にも示されています. (論文では図があるだけで特に細かい言及があるわけではないです)

これはDPM-Solverの例ですが, $a=20$ 以降では完全に違う生成結果になっています. できるだけ生成例を変えたくない場合は $a=10$ あたりが無難な設定でしょうか. AppendixにはDDIMでの生成例も示されていますが, どちらの場合も大体 $a=\dfrac{2}{5}T$ とするのが良さそうです.

まとめ

• denoising processでは全体の生成から細部の生成へと対象が変化する
• テキスト情報もdenoising processの序盤で伝達され, 後半はそれまでの生成結果を基にモデルが細部を詰めていく
• よって, テキスト情報を与えるのは途中までにすることで高速化ができ, 全体で25％程度の計算コスト削減につながった

参考文献

• Yogesh Balaji, Seungjun Nah, Xun Huang, Arash Vahdat, Jiaming Song, Qinsheng Zhang, Karsten Kreis, Miika Aittala, Timo Aila, Samuli Laine, Bryan Catanzaro, Tero Karras, and Ming-Yu Liu. ediff-i: Text-to-image diffusion models with an ensemble of expert denoisers, 2023.
• Amir Hertz, Ron Mokady, Jay Tenenbaum, Kfir Aberman, Yael Pritch, and Daniel Cohen-Or. Prompt-to-prompt image editing with cross attention control, 2022.
• Yang Song, Jascha Sohl-Dickstein, Diederik P Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. Score-based generative modeling through stochastic differential equations. In International Conference on Learning Representations, 2021.
• Guangxuan Xiao, Yuandong Tian, Beidi Chen, Song Han, and Mike Lewis. Efficient streaming language models with attention sinks. In The Twelfth International Conference on Learning Representations, 2024.
• Mingyang Yi, Aoxue Li, Yi Xin, and Zhenguo Li. Towards understanding the working mechanism of text-to-image diffusion model, 2024.
• Wentian Zhang, Haozhe Liu, Jinheng Xie, Francesco Faccio, Mike Zheng Shou, Jürgen Schmidhuber. Cross-Attention Makes Inference Cumbersome in Text-to-Image Diffusion Models, 2024.

脚注

1. 同じ方が第一著者のDigital Image Processing 4th Editionが公開されていたりします