Stable Diffusionからの概念消去㉖: CURE（論文）

CURE: Concept Unlearning via Orthogonal Representation Editing in Diffusion Models (NeurIPS2025)

今年も早いもので, 残りのメジャー会議もNeurIPSくらいになりました. そこで採択された概念消去の論文を確認します.

書籍情報

断りのない限りは以下の論文から図表を引用しています.

Shristi Das Biswas, Arani Roy, and Kaushik Roy. Cure: Concept unlearning via orthogonal representation editing in diffusion models. arXiv preprint arXiv:2505.12677, 2025.

関連リンク

• arXiv
• NeurIPSのページ
• Project Page
• GitHub

概要

CUREは閉形式で更新を行う手法で, 著者らによれば2秒でできるそうです. これ以上閉形式の手法が出てくるとは思ってもいませんでしたが, どこが新しいのか見ていきたいです. 著者らが主張する貢献は3つで

• 直行射影とスペクトル幾何を利用したSpectral Eraserを用いて消去を行う
• 古典的な正則化理論に基づく選択的特異値展開機構（selective singular-value Expansion Mechanism,）を新たに導入し, 概念消去とその他の概念保持を両立することに成功した
• 実験結果がとてもよかった

最後のはさておき, 手法の核となりそうなのは上2つです. それぞれ見ていきます.

準備

手法に立ち入る前に, 前提を確認します. 拡散モデルでテキストの情報を伝える際にはcross attentionが用いられます. 各トークン埋め込みを $\mathcal{E}_i$, とすると, attentionの計算で必要なkeyとvalueは

$$k_i=W_k\mathcal{E}_i,\quad v_i=W_v\mathcal{E}_i$$

です. 言うまでもないですが, $W_k, W_v$ は線形層の重みです. ここで大事なのは, keyやvalueが時刻情報と画像情報を必要としていない点です. ここに着目します.

問題設定

論文では小難しく述べられていますが, 定式化を行います. $\mathcal{U}$ をtext encoderによって表現可能な概念の全体集合 (universal set)とします. $\mathcal{U}$ の内部にあって, target concept $c_f$ を含む部分集合を $\mathcal{F}\subseteq\mathcal{U}$ とします. 保持したい概念 $c_r$ も同様に $\mathcal{R}\subseteq\mathcal{U}$ とします. ここで, $\mathcal{F}\cap\mathcal{R}\neq\emptyset$ であることに注意します.

識別的部分空間の構築

$\mathcal{F}$ と $\mathcal{R}$ を, text encoderを介してユークリッド空間に埋め込みます. $\mathcal{F}$ と $\mathcal{R}$ の各概念について, 対応するprompt tokenからtarget embedding $\mathcal{E}_f, \mathcal{E}_r$ を得ます. これらのembeddingに対して, 直交正規基底ベクトルを用いて特異値分解 (SVD)を行います. これによって

$$\mathcal{E}_f=\mathcal{U}_f\Sigma_f\mathcal{V}^\top_f,\quad\mathcal{E}_r=\mathcal{U}_r\Sigma_r\mathcal{V}^\top_r$$

を得ます. ややこしいですが, 論文では

characterized by the orthonormal basis vectors $\mathcal{U}$ for each embedding

と書かれており, 先ほど定義した集合とは異なる $\mathcal{U}$ であることが示唆されます（これは一般的な特異値分解の式に合わせて $\mathcal{U}, \mathcal{V}$ を使っていると思われますが, 同じ記号を異なる意味で使うことは混乱の元ではないかと私は思います）.

このことから, $\mathcal{F}$ の空間と $\mathcal{R}$ の空間は形式的に $\mathcal{S}_{\mathcal{F}}=\mathrm{span}(\mathcal{U}_{f}), \mathcal{S}_{\mathcal{R}}=\mathrm{span}(\mathcal{U}_{r})$ と表現されます. 幾何学的には, 各概念に関する情報が最も強く符号化されている部分空間内の方向を表しています.

続いて, 任意の埋め込み $\mathcal{E}_i\in\mathbb{R}^d$ をこれらのベクトル空間に射影することを考えます. ナイーブな方法として $\mathcal{P}_f=\mathcal{U}_f\mathcal{U}^\top_f$ や $\mathcal{P}_r=\mathcal{U}_r\mathcal{U}^\top_r$ によって射影することが考えられますが, $\mathcal{P}_f, \mathcal{P}_r$ は重みづけが等方的で, 各基底ベクトルの重要性に応じたスケーリングを考慮していないことが問題としてあります. 等方的な重みづけは, 重要な概念方向と単なる偶然の相関を区別する相対的なスペクトルエネルギーである $\Sigma_f, \Sigma_r$ を無視しています. ただし, より大きな特異値に対応する特定の方向が他の方向よりも概念の顕著な特徴や支配的な側面をよりよく表現している場合も実際にはあることに注意が必要です.

このことへの対処として著者らは, 基底ベクトルの相対的な重要性に基づいて重みづけを行うエネルギースケーリング機構を組み込んだ, 射影演算子を提案しています. 具体的には, 埋め込みの共分散構造を $\mathcal{E}\mathcal{E}^\top=\mathcal{U}\Sigma^2\mathcal{U}^\top$ として計算します. ここで $\Sigma^2$ は特異値の2乗を対角成分とする対角行列で, 各成分のエネルギー情報を符号化しています. これによって重要性を反映した射影演算子を作成することができる. この演算子はベクトル方向のスケーリングをスペクトルの大きさに応じて行うもので

$$\mathcal{P}_f=\mathcal{U}_f\Sigma^2\mathcal{U}^\top_f,\quad \mathcal{P}_r=\mathcal{U}_r\Sigma^2\mathcal{U}^\top_r$$

と書けます.

スペクトル拡張機構

先程の話には1つの課題があります. 共分散行列の対角構造は各成分にわたるエネルギー分布 $(\sigma^2_i)$ を自然と明らかにしますが, 部分空間方向の選択を, 厳密なエネルギー階層に結びつけてしまいます. これはエネルギーに対する重みづけの柔軟性を欠き, 概念消去における消去強度の自由度を奪ってしまいます. このことへの対処として, 著者らはSpectral Expansion mechanism （以下スペクトル展開機構）を提案しています. これは, target conceptとして選択される特異成分の割合を調整します. 形式的にはチホノフ正則化（Tikhonov regularizer）に着想を得ており, 調整可能なパラメータである $\alpha$ を導入して相対的なスペクトルエネルギーのスケールを調整します. 具体的には $r_i=\dfrac{\sigma^2_i}{\sum_j\sigma^2_j}$ を正則化されたスペクトルエネルギーとして

$$f(r_i;\alpha)=\dfrac{\alpha r_i}{(\alpha-1)r_i+1}$$

と定義されます. $\alpha$ は $\alpha\to1$ の場合における比例重み付けと $\alpha\to\infty$ の場合における支配的なモード増幅とのトレードオフを調整します. 直感的には, $\alpha$ が大きくなるにつれて, $f(r_i;\alpha)$ は $r_i$ の相対的な大きさに対する感度が低下し, non-zero成分を全て等しい重要度に飽和させる働きをします. これによって, 識別力が低いベクトルも支配的なベクトルと同様に消去に働きかけることが可能になります. つまり, $\alpha$ が大きいほど部分空間のより広い領域を除去することになります. これによって広範な消去が可能になりますが, 細かい制御性は犠牲になります.

最終的には

$$\mathcal{P}_f=\mathcal{U}_f\Lambda_f\mathcal{U}^\top_f, \quad\mathcal{P}_r=\mathcal{U}_r\Lambda_r\mathcal{U}^\top_r$$

となります. ここで, $\Lambda_f=\mathrm{diag}(f(r^{(f)}_i;\alpha)), \Lambda_r=\mathrm{diag}(f(r^{(r)}_i;\alpha))$ です.

閉形式によるスペクトル消去

$\mathcal{P}_f, \mathcal{P}_r$ がわかると, 以下の方法によって概念消去が可能になります.

$$\mathcal{P}_{\mathrm{unlearn}}\coloneqq\mathbb{I}-\mathcal{P}_{\mathrm{dis}},\quad \mathcal{P}_{\mathrm{dis}}=\mathcal{P}_f-\mathcal{P}_f\mathcal{P}_r$$

これによる更新は埋め込み $\mathcal{E}$ に作用し, 更新後の埋め込み $\mathcal{E}_{\mathrm{new}}=\mathcal{P}_{\mathrm{unlearn}}\mathcal{E}$ となります.

消去演算子の重み空間への吸収

推論中に, $\mathcal{P}_{\mathrm{unlearn}}$ をトークンごとに動的に適用する代わりに, 先ほど定めた演算子をモデルに組み込みます. 当然cross attentionの部分に適用するわけですが, 以下のように計算を行います.

$$W_k^{\mathrm{new}}=W_k\mathcal{P}_{\mathrm{unlearn}},\quad W_v^{\mathrm{new}}=W_v\mathcal{P}_{\mathrm{unlearn}}$$

ここまでの流れを図にすると以下のようになります.

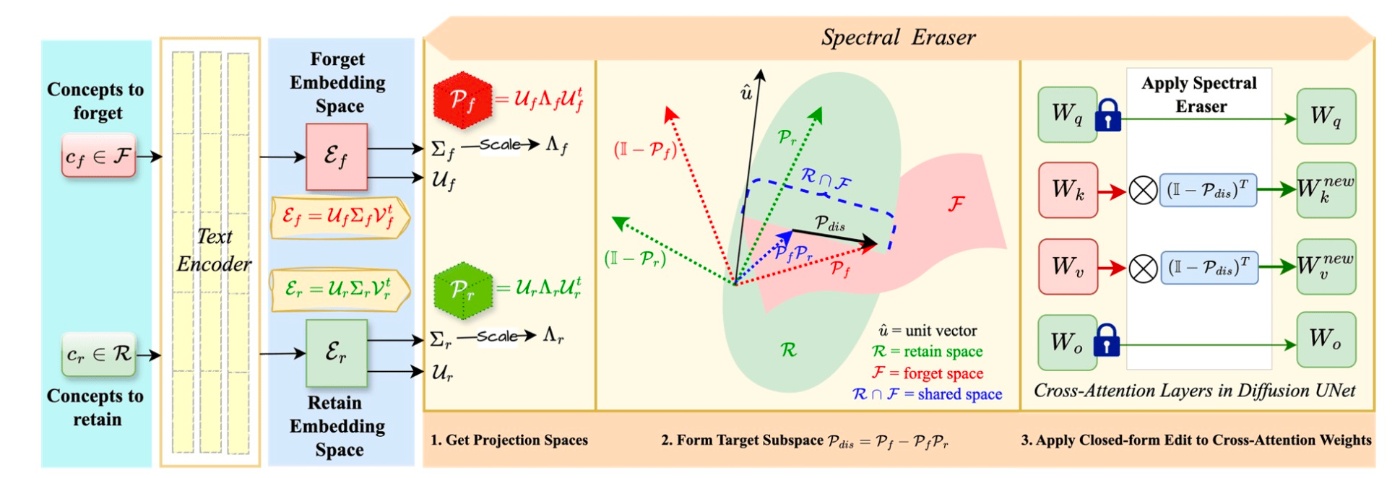
実験

いつものように, 設定を確認してから結果を確認します. 多くの既存研究と同様に, style, object, identity (celebrity), unsafe contents (NSFW), および堅牢性についてを確認します. ベースモデルはStable Diffusion 1.4です. ハイパーパラメータである $\alpha$ は, NSFWのみ $\alpha=5$ とし, 残りの場合は $\alpha=2$ で実験が行われています.

styleの消去

先行研究でも用いられている代表的なstyleを10個選んで実験します. 1つの概念につき20個のプロンプトを用意します. 定量評価としてVan GoghとKelly McKernanについて結果を示します. 評価指標として $\text{LPIPS}_\text{e}, \text{LPIPS}_\text{u}$ を使用しています. また, LLM-as-a-judgeとしてGPT-4oによるstyleの分類を行います. ここにおける評価は $\text{ACC}_\text{e}, \text{ACC}_\text{u}$ です. 当然, MSCOCO-30KでFIDとCLIP Scoreも測定します.

結果を確認します.

著者らの主張によれば, 他の概念への影響を最小限に抑えつつ, 消去性能はベースラインを上回るとのことです. 本当にそうでしょうか...と言いたくなる結果ですが, 下図(a)を見ても, 確かに他の概念への影響は少なく, かつ消去性能はいいように見えます.

また, 上図(b)からは堅牢性も確認できます.

NSFWの消去

例によって, I2P datasetでの実験です. ここでもNudityの消去のみを行なっています. 検出はNudeNetです.

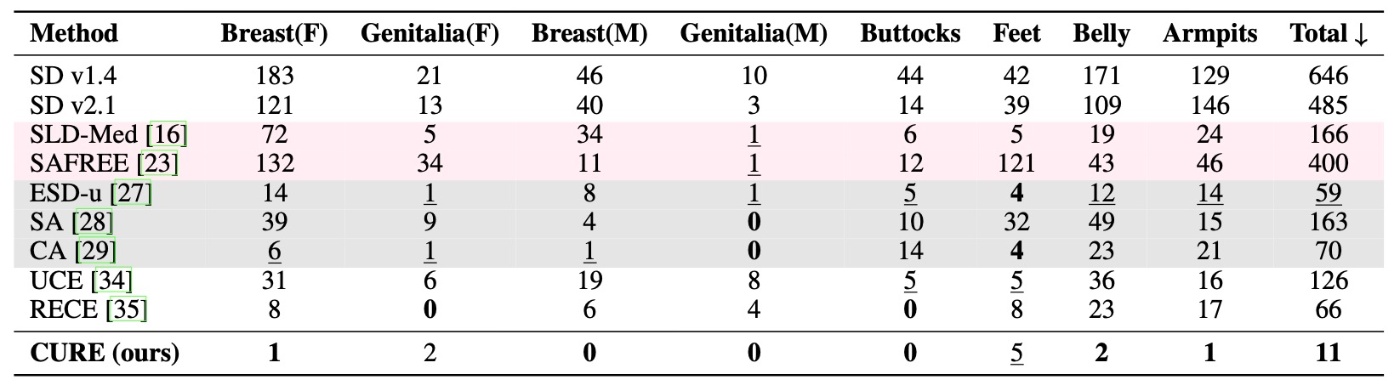
結果を見るとわかりますが, ほぼ消去に成功していそうな雰囲気です. 著者らは,

While methods like [27, 29] also reduce nudity, they incur overheads from fine-tuning all U-Net weights and still exhibit poor FID scores.

と述べていますが, 少なくともこれを裏付ける実験結果は示されていません. CAでは3種類のtuning手法が提案されていますし, この論文ではESDとESD-uは表記上は使い分けられており, ならば前者はESD-x (cross attentionのみを更新)と解するのが自然だからです. また, この部分が正しく表記されていたとしても, U-Net全体の更新によるオーバーヘッドが大きいこと結果とはあまり関係がないです (すくなくとも論文からはそう言えると思います).

また, いつものようにさまざまな攻撃手法に対しても実験を行なっています.

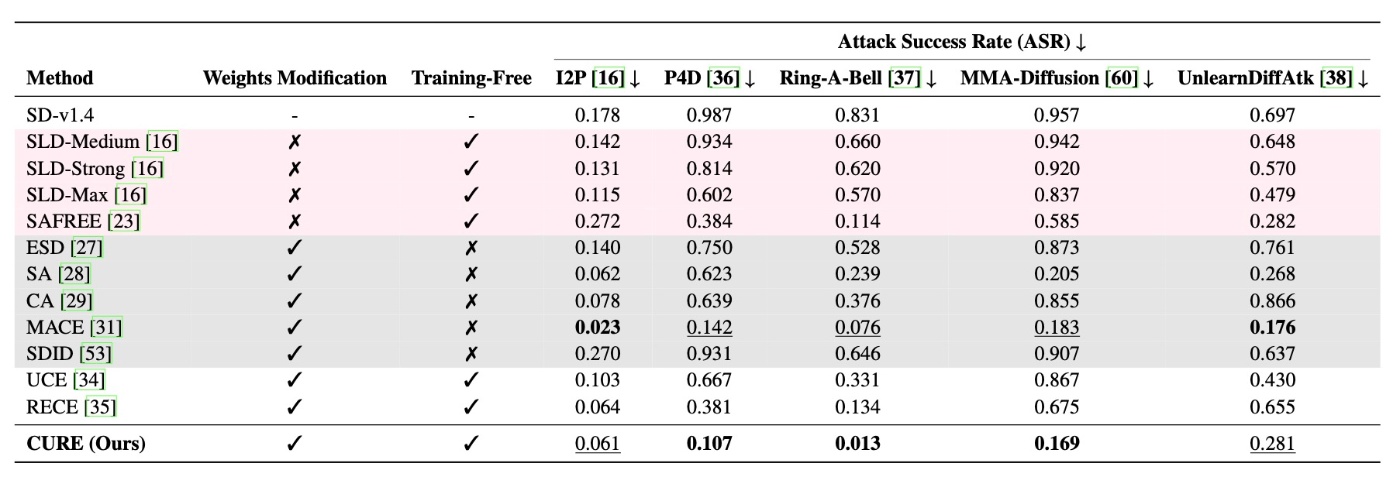
かなり低いASRです. 著者らはcaptioningで

Robustness of all methods against red-teaming tools, measured by Attack Success Rate (%).

としていますが, UnlearnDiffAtkの結果を見るに

https://eccv.ecva.net/virtual/2024/poster/1775

%ではないです. %にするにはこれを100倍する必要があるように思えます. そうでなければあらゆる消去手法が1%未満のASRとなってしまいます.

objectの消去

こちらもお馴染みとなっているImagenetteを使用します. 500枚の画像を生成してResNet-50で分類します. 結果を見てみます.

結果を見るとそれなりによさそうです. 個人的には概念消去には順序があって

1. target conceptを消すことができる
2. target conceptが消せている状態で他の概念に影響がない

なので, この結果で優位性を主張するには無理があるのかなと思います.

Identityの消去

いわゆるcelebrityの消去にあたります. GIPHY Celebrity Detectorでのtop-1 accuracyで評価します, と論文では述べられていますが, 定量評価は見当たりません. 追加結果はAppendixとも述べられていますが, そこにも定量評価の結果は見当たりません. そのかわりと言ってはなんですが, 定性結果を見ておきます.

ここではJohn Wayneを消した時の結果が示されています. 著者らはJohn Wayneを消した際に, 他の手法ではfirst nameが一致するJohn Lennonの維持が難しいとしています. 確かに提案手法ではその区別がされてJohn Lennonは維持されてJohn Wayneは消えているように見えます. ただ, この現象自体は比較対象にもあるMACEの論文で既に触れられている話題であり, 特段新規性があるようには見えません.

https://openaccess.thecvf.com/content/CVPR2024/html/Lu_MACE_Mass_Concept_Erasure_in_Diffusion_Models_CVPR_2024_paper.html

消去効率

最後に消去効率を見ておきましょう. 実際のユースケースにおいてはたくさんの概念を消去したいため, 1概念あたりに要するコストは小さい方がいいです.

A40 GPU上での結果を確認すると, 結構高速に動作することがわかります. ただ, UCEはそれよりさらに速いですし, objectにおける他の概念の維持など提案手法に優っている部分もあり, 必ずしも提案手法が優れているとは言えなさそうです.

思ったこと

• 査読結果を見られていないのでコメントに困るところですが, 個人的にはNeurIPSなのかな..という気持ちです. 確かに提案手法はこれまでの閉形式の手法に手を加えたもので新規性があり, 性能面でもcompetitiveくらいにはなっています. 一方で, その手を加えた部分に見合った結果が出ているのかというと微妙なのではないかと思っています. Ablationで示せるとよさそうです (ablationは論文にはありませんでした).
• それに関連して, 比較対象があまり新しくないことが気になります. 既にESDやSLDは拡散モデルの概念消去において初期の研究ですから, 生成タスクに例えればDDPMやLDMとメインで比較しているような印象です. もちろん出発点に近い研究なので評価の表に載せるのは問題ないと思いますが, 参考程度の話ではないかと思います. 必ずしも最新の研究と比較する必要はないと思いますが, その選定理由 (特にrelated worksで引用した研究を選ばなかった理由)くらいは欲しいですね.

参考文献

• Lu, S., Wang, Z., Li, L., Liu, Y., and Kong, A. W.-K. Mace: Mass concept erasure in diffusion models. In Proceed- ings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 6430–6440, June 2024.
• Shristi Das Biswas, Arani Roy, and Kaushik Roy. Cure: Concept unlearning via orthogonal representation editing in diffusion models. arXiv preprint arXiv:2505.12677, 2025.