Stable Diffusionからの概念消去㉕：Minimalist Concept Erasure（論文）

Minimalist Concept Erasure in Generative Models (ICML2025)

ICMLでまだ読んでいなかった論文を発見したので扱います. この手の論文にしては珍しく日本人と思しき方の名前が確認できます.

書籍情報

断りがない限りは以下の論文から図表を引用します.

Yang Zhang, Er Jin, Yanfei Dong, Yixuan Wu, Philip Torr, Ashkan Khakzar, Johannes Stegmaier, and Kenji Kawaguchi. Minimalist concept erasure in generative models. In Forty-second International Conference on Machine Learning, 2025.

関連リンク

公式実装はなさそうです.

• arXiv
• OpenReview

はじめに

今回扱う手法はFLUXがターゲットです. そこで, Rectified Flowについて簡単に触れます. Rectified Flowはある分布 $p_0(\bold{x})$ から別の分布 $p_1(\bold{x})$ へのフローを学習します. 簡単に言えばどのようなルートを通ればいいかを学習しています. このフロー $\psi_{t}(\bold{x})$ は時間変化するベクトル場 $u_{t}(\bold{x}_t)$ を用いて

$$\dfrac{d}{dt}\psi_{t}(\bold{x})=u_t(\psi_{t}(\bold{x})),\quad t\in[0,1]$$

と書けます. 我々はデータセットを通してtarget分布 $p_1$ から $X_1$ を得ることができます. すなわち

$$dX_t=v_t(X_t)dt,\quad X_0\sim p_0$$

という形に帰着できます. このベクトル場 $v_t$ をNNで近似し, ODEを用いることで $X_0$ から $X_1$ を推定できます. 学習では単に $t:(1-t)$ で内分した点 $X_t=tX_1+(1-t)X_0$ を予測します. 損失関数はMSEで

$$\mathcal{L}(\theta)=\mathbb{E}[\|u_t(X_t|X_1)-u_{\theta}(X_t, t)\|_2^2]$$

となります.

Minimalist Concept Erasureの問題定義

まずはこの論文で掲げられている問題設定を確認します. と言っても, いつもの感じで「消したい概念は消し, その他の概念は維持する」という感じです. 任意の概念を含む集合を $\mathcal{C}_N$, 消したい概念のみを含む集合を $\mathcal{C}_R$ としたとき,

$$\min_{\theta}\mathbb{E}_{c\sim\mathcal{C}_{R}}[\mathbb{E}_{x_0\sim p_\theta(\bold{x}_0|c)}[\log p_{\theta}(c|x_0)]]+\beta\mathbb{E}_{c\sim\mathcal{C}_{N}}[\mathbb{D}_{\mathrm{KL}}[p_{\theta'}(\bold{x}_0|c)\| p_{\theta}(\bold{x}_0|c)]]$$

となるパラメータ $\theta$ を見つけることです. ここで $\theta'$ はoriginalのパラメータです. 見た通りで, 先ほど言葉にした「消したい概念は消し, その他の概念は維持する」を数式で表したにすぎません. しかし, 著者らは論文でboldな文字を用いてまで既存研究との差異を強調しています. それは, 既存研究では生成過程も考慮しているが, この論文では最終的な出力のみを考えるということです. 図にすると下のようになります.

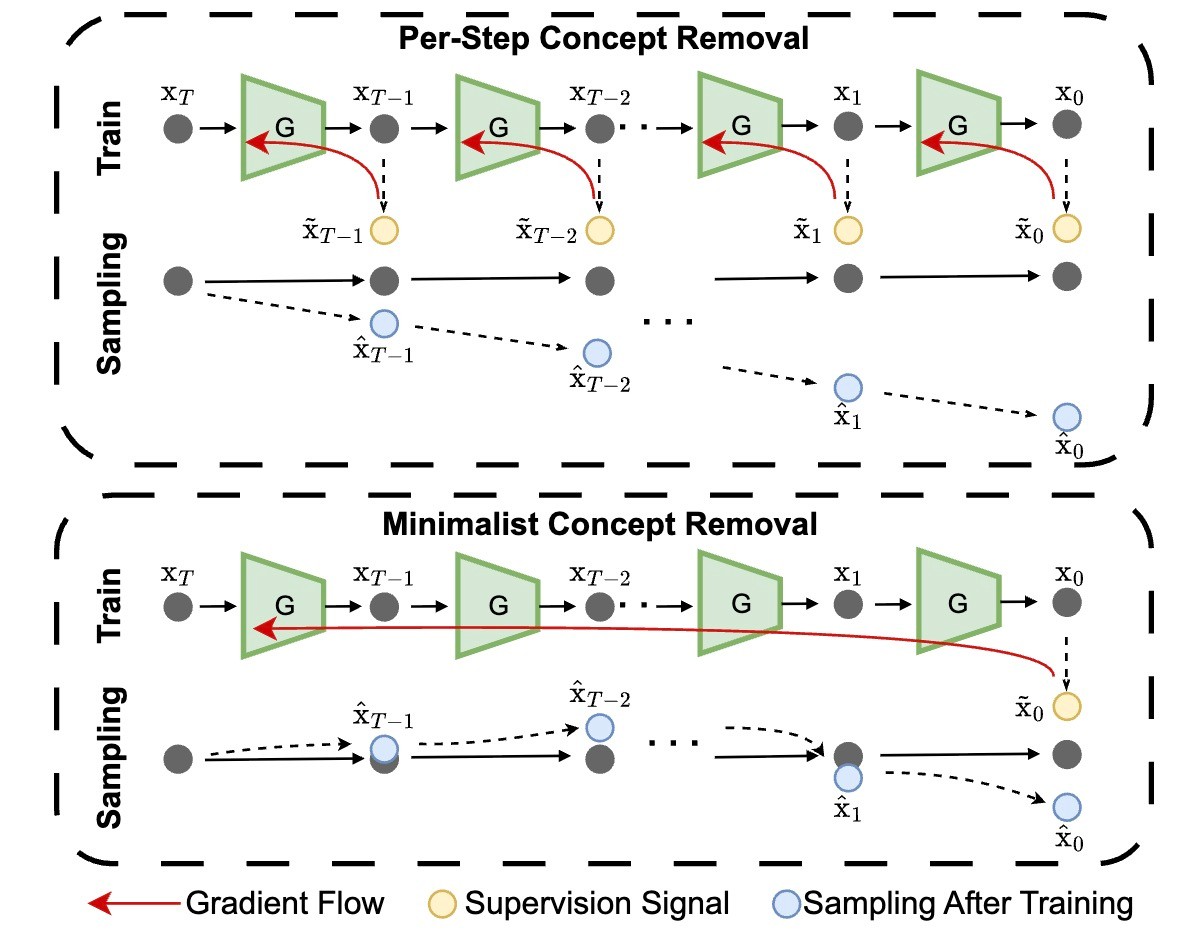
既存研究は上のPer-Step Concept Removalです. これは徐々にその概念の軌跡から外れていくという形式です. 対して提案手法は下に示されていますが, 途中まではoriginal modelのままを辿り, 最後に外れます.

ここで, 「本当にそんなことが可能なのか？」という疑問が出ます（私は思いました）. 生成プロセスを考えるとRectified Flowであっても拡散モデルと同様に, 全体から細部という構造は変化しないからです. 実際, Rectified Flowの論文で示されている図でも中盤あたりの $t$ でtarget分布の影響を確認できます.

Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flowより引用

そのあたりにも注目しながら提案手法を見ていきます.

損失関数の派生

先ほど定義した最適化問題ですが, KLの項があります. これは計算が大変なので変形していきたいです.

preservation loss

まずは他の概念の方を変えます. 係数 $\beta$ はさておき

$$\mathcal{L}_p=\mathbb{E}_{c\sim\mathcal{C}_{N}}[\mathbb{D}_{\mathrm{KL}}[p_{\theta'}(\bold{x}_0|c)\| p_{\theta}(\bold{x}_0|c)]]$$

の形をしていました. 最初にsource分布 $p(x_T)$ を導入し, KLダイバージェンスを分解していきます.

$$\mathbb{D}_{\mathrm{KL}}[p_{\theta'}(\bold{x}_0|c)\| p_{\theta}(\bold{x}_0|c)]\leq\mathbb{E}_{x_T}[\mathbb{D}_{\mathrm{KL}}[p_{\theta'}(\bold{x}_0|x_T,c)\| p_{\theta}(\bold{x}_0|x_T,c)]]$$

となります.

Rectified Flowのモデルは生成プロセスが決定的です. そこで, 初期ノイズ $x_T$ が与えられた時に最終的に生成される画像 $\bold{x}_0$ は小さい分散 $\Sigma$ のガウス分布に従うと仮定しています (この仮定が正しいかは怪しい気がしますが). 数式的には

$$p_{\theta}(\bold{x}_0|x_T, c)=\mathcal{N}(\bold{x}_0|\mathcal{F}_{\theta}(x_t, c), \Sigma)$$

です. $\mathcal{F}$ はflowのサンプリング過程全体にオイラー法を適用したもので表され,

$$\mathcal{F}_{\theta}(x_t, c)=x_T+u_{\theta}(x_T, T, c)\Delta T+u_{\theta}(x_T+u_{\theta}(x_T, T, c), T-\Delta T, c)\Delta T+\ldots$$

のようになっています. Rectified Flowの定式を取り入れることで

$$\mathbb{E}_{x_T}[\mathbb{D}_{\mathrm{KL}}[p_{\theta'}(\bold{x}_0|x_T,c)\| p_{\theta}(\bold{x}_0|x_T,c)]]=\mathbb{E}_{x_T}[\mathbb{D}_{\mathrm{KL}}[\mathcal{N}(\bold{x}_0|\mathcal{F}_{\theta}(\cdot),\Sigma)\| \mathcal{N}(\bold{x}_0|\mathcal{F}_{\theta'}(\cdot),\Sigma)]]$$

となります. KLダイバージェンスの性質と, 2つのガウス分布に対して等方的な共分散行列 $\sigma^2I$ を仮定すると,

$$\mathcal{L}_p\leq\dfrac{1}{2\sigma^2}\mathbb{E}_{c, x_T}[\|\mathcal{F}_{\theta}(x_T, c)-\mathcal{F}_{\theta'}(x_T, c)\|_2^2]$$

となります.

erasure loss

さて, 最適化問題の最初の項に着目します.

$$\mathcal{L}_r=\mathbb{E}_{c\sim\mathcal{C}_{R}}[\mathbb{E}_{x_0\sim p_\theta(\bold{x}_0|c)}[\log p_{\theta}(c|x_0)]]$$

ベイズの定理から

$$\mathcal{L}_r=\mathbb{E}_{c\sim\mathcal{C}_{R}}\left[\mathbb{E}_{x_0\sim p_\theta(\bold{x}_0|c)}[\log \dfrac{p_{\theta}(x_0|c)}{p_{\theta'}(x_0)}]\right]+C=\mathbb{E}_{c\sim\mathcal{C}_{R}}[\mathbb{D}_{\mathrm{KL}}[p_\theta(\bold{x}_0|c)\| p_{\theta'}(\bold{x}_0)]]+C$$

となります. $C$ は定数です. ここから, 定数項を除去し, preservation lossと同様にすると

$$\mathcal{L}_r\leq\dfrac{1}{2\sigma^2}\mathbb{E}_{c\sim\mathcal{C}_R, x_T}[\|\mathcal{F}_{\theta}(x_T, c)-\mathcal{F}_{\theta'}(x_T, \emptyset)\|_2^2]$$

となります. すなわち, 問題設定で定義した最適化問題は

$$\mathcal{L}=\mathbb{E}_{c\sim\mathcal{C}_R, x_T}[\|\mathcal{F}_{\theta}(x_T, c)-\mathcal{F}_{\theta'}(x_T, \emptyset)\|_2^2]+\beta\mathbb{E}_{c\sim\mathcal{C}_N, x_T}[\|\mathcal{F}_{\theta}(x_T, c)-\mathcal{F}_{\theta'}(x_T, c)\|_2^2]$$

を最小化することで解くことができます. 訓練中はこの推定値を得るためにモンテカルロ法を使用します.

ちなみにこれはRectified Flowに対する損失関数ですが, フロー系のモデルと拡散モデルには論理的な等価性が存在するのでこの損失を少し変えるだけで拡散モデルにも適用可能です. また, 他の概念消去の手法と同様に各タイムステップにおいての消去も実現することができます. ちなみに, 論文ではRLHFとの関連も述べられていますがここでは省略します.

実装

実際の訓練では, SalUnなどと同様にどのニューロンを更新するかのmaskを作成して重みの更新をします. また, $\mathcal{F}$ の計算からわかるように, 長い勾配連鎖になっています. 連鎖律に従うとmask勾配は

$$\dfrac{dL(X_0, \tilde{X}_0)}{dM}\coloneqq\sum_{i}\dfrac{dL(X_0(X_i), \tilde{X}_0)}{dX_i}\dfrac{dX_i}{dM}$$

です. 以下の研究によるとステップごとにgradient checkpointを実施することでステップ数に依存せずにメモリ消費量を一定に抑えることができるようです. 以降の実験でもこれを用いています.

https://openreview.net/forum?id=y1LE41gGWS

実験

いつも通り, 設定を確認します. 著者らの計算資源の都合からtime-stepで蒸留されたFLUX.1-Schnellを使用します. ベースラインとしては, ESD, CA, SLD, EAPを用います. 画像編集であるFlowEditも比較対象としています. 評価にはLLaVAを用いた検出率, CLIP Score, SSIM, FIDを使用します. ただし, FIDなどはいつものMSCOCO-30kではなくLAION-5kです.

まずは定量評価を確認します.

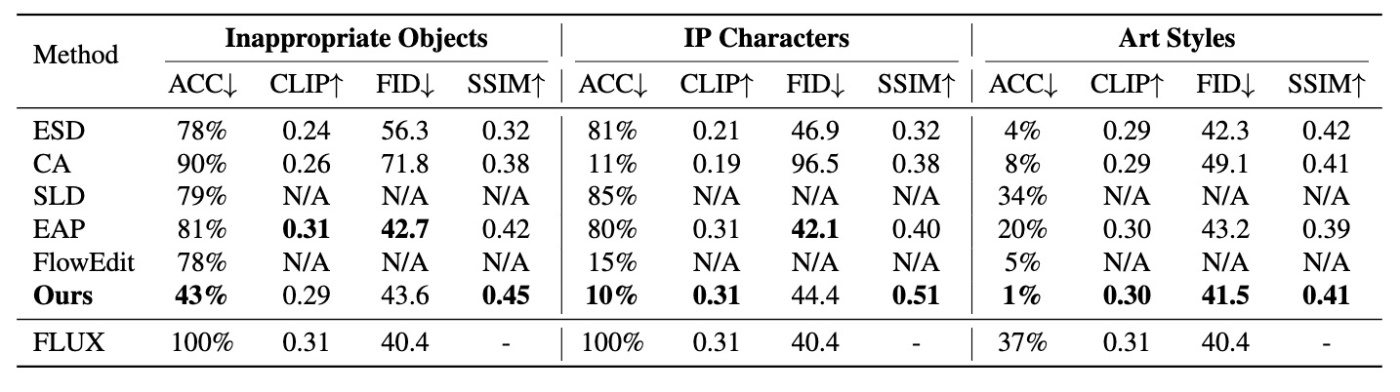
Inappropriate Objects (gun knife, drug)に関しては消去性能で他の手法を圧倒していますが, IP/Artではそこまでというような結果です. Artに関してはSSIMでESDに劣っていますがboldedになっています. 生成例を見てみます.

この結果を見る限りでは提案手法は高い性能を見せています.

続いて, ロバストさを確認するため, Ring-A-Bell, MMA-Diffusion, P4D, I2Pでの攻撃実験を行います.

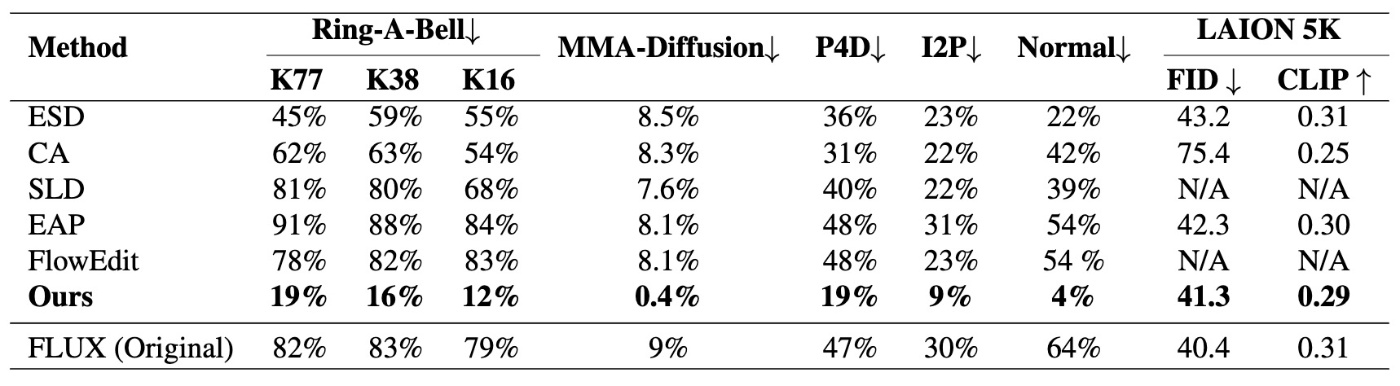
こちらは他の手法と比較してロバストであることがわかります. が, I2Pは自分の体感だとSoTAモデルではもっと低いように思えるのでもしかしたらそこまでではないのかもしれないです.

思ったこと

• 最後さえ合っていればいいというのは新しい考え方ですが編集タスクには非常に脆弱そうな印象を受けます. その比較が気になります.
• Rectified Flowだけでなく拡散モデルも同じように議論できるのは嬉しいです.
• 生成途中の結果がないので気になった部分は自分で実験するしかなさそうです. こういうときのためにも実装は公開しておくべきだなと改めて思いました.
• 実験面ではベースラインが弱い気がしています. 拡散モデルにも適用可能なのですから, そこで実験して性能の高さを示せるとより万能な感じが出るように思えます.

参考文献

• Yang Zhang, Er Jin, Yanfei Dong, Yixuan Wu, Philip Torr, Ashkan Khakzar, Johannes Stegmaier, and Kenji Kawaguchi. Minimalist concept erasure in generative models. In Forty-second International Conference on Machine Learning, 2025.
• Xingchao Liu, Chengyue Gong, and qiang liu. Flow straight and fast: Learning to generate and transfer data with rectified flow. In The Eleventh International Conference on Learning Representations, 2023.