新たなGANのベースライン

はじめに

みなさんGANは知っていますか？この記事を読むような人は知っていると思いますが, 拡散モデルが流行る前はGANが画像生成分野を席巻しており, それこそさまざまな分野に転用されたりしていました. GANを日本語で説明する際にはよく「偽札製造と見破る警察官」のような喩えをされたりします. その喩えの通り, GANではなにかデータが与えたれた場合にそれが実データか生成データかを判定するDiscriminatorと, データを生成するGeneratorの2種類のネットワークがあり, 学習においてはGeneratorはDiscriminatorを騙すように, 逆にDiscriminatorは完璧に判定するようにネットワークを最適化します. 定式化すると, GeneratorとDiscriminatorをそれぞれ $G_{\theta}$, $D_{\psi}$ とし, 実データ $x$ が確率分布 $p_{\mathcal{D}}$ に, 生成データ $x$ が確率分布 $p_{\theta}$ に従うとするとき,

$$\mathcal{L}(\theta, \psi)=\mathbb{E}_{z\sim p_{z}}[f(D_{\psi}(G_{\theta}(z)))]+\mathbb{E}_{x\sim p_{\mathcal{D}}}[f(-D_{\psi}(x))]$$

を損失関数とします. この定式化を見ればわかるように複雑です. 実際にGANの学習は難しく, 「これさえ生成しておけばDiscriminatorは騙せる」とGeneratorが誤った学習をした結果, モード崩壊などが起こったりします. 逆に, 「何を生成しても騙せない」という状況も起こったりします. GANの登場以後しばらくはアーキテクチャ改良の他にもそのような学習の不安定性を解消する試みが研究されていたと私は思っています.

一方で2015年に発表されて以後特に進展のなかった拡散モデルですが, 2020年にDDPMという手法が登場し, 以下の非常に簡単な損失関数で安定的に学習が可能であることがわかりました.

$$\mathbb{E}_{t\sim\mathcal{U}[1, T], \boldsymbol{\varepsilon}\sim\mathcal{N}(0, 1), \bold{x}_0\sim p_{\mathcal{D}}}\left[\|\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}_{\theta}(\sqrt{\overline{\alpha}_t}\bold{x}_0+\sqrt{1-\overline{\alpha}_t}\boldsymbol{\varepsilon}, t)\|_2^2\right]$$

この論文以降, 様々な改良が研究され, Stable Diffusionなどのオープンウェイトのコミュニティ資産も登場したお陰で拡散モデルはGANを駆逐したと言っていい状況です.

今回扱う論文The GAN is dead; long live the GAN! A Modern Baseline GANでは, これまでのGAN研究で有効だとみなされてきた手法を採用せず, シンプルなアーキテクチャと改良された損失関数で拡散モデル（EDMなど）に匹敵することを示していきます.

書籍情報

Nick Huang, Aaron Gokaslan, Volodymyr Kuleshov, and James Tompkin. The GAN is dead; long live the GAN! a modern GAN baseline. In The Thirty-eighth Annual Conference on Neural Information Processing Systems, 2024.

関連リンク

• arXiv
• OpenReview
• 公式実装
• 学習済みモデル (HuggingFace)

現在のGAN

主題に入る前に簡単に現状のGANがどのようなアーキテクチャになっているのか見ていきます. GANといえばお馴染みという感じのStyleGANはStyleGAN1, 2, 3の3種類が直系（Tero Karras氏が1st author）と言えるもので, それぞれGeneratorは以下のようなアーキテクチャをしています.

Face Generation and Editing with StyleGAN: A Surveyより引用

他にもテキストからの生成に対応したStyleGAN-Tなどがあります.

StyleGAN-T: Unlocking the Power of GANs for Fast Large-Scale Text-to-Image Synthesisより引用

これはDiscriminatorのアーキテクチャまで入っているので一緒くたに比べることはできないですが, 結構複雑になってきています. The GAN is dead; long live the GAN! A Modern Baseline GANの2nd authorであるAaron Gokaslan氏はTwitter (X)で

https://twitter.com/SkyLi0n/status/1877824426495840343

と述べています. これはStyleGAN以降の発展が全てStyleGANがベースとなっているのでこのアーキテクチャを捨てられないということなのではと思います.

安定性と多様性

GANで画像生成を行う際に解決すべき2つの主要な課題があります. 学習の安定性と生成品質の多様性です. 著者らはRpGAN$+R_1+R_2$で解決しようとしています. RpGAN$+R_1+R_2$ なので提案手法はR3GANという名前です. それではそれぞれ見ていきます.

RpGAN

RpGAN (オリジナルの論文ではRGANと呼ばれている)は

https://openreview.net/forum?id=S1erHoR5t7

です. ここでは損失関数を以下のように定めます.

$$\mathcal{L}(\theta, \psi)=\mathbb{E}_{z\sim p_{z}x\sim p_{\mathcal{D}}}[f(D_{\psi}(G_{\theta}(z))-D_{\psi}(x))]$$

従来のGANではDiscriminatorが実データと生成データを見分けます. 生成データと実データが単一の決定境界で分断される場合, Generatorはその境界を少しだけ超えるようにデータを生成することで学習が進みます. この現象が多数のデータで起こることでモード崩壊が観測されると著者らは述べています. 実際, 既存研究

https://papers.nips.cc/paper/2020/hash/738a6457be8432bab553e21b4235dd97-Abstract.html

においても, このような解が $\mathcal{L}$ の地形におけるbad local minima （日本語にすると悪い局所最小値、といった感じでしょうか）として特徴付けており、従来のGANの損失関数には 指数的に多数 の「悪い局所最小値」が存在することを示しています.

この問題の原因はどこでしょう？先ほどまでの話の流れから, 実データと生成データを分類する際に生じる単一の決定境界と考えられます. RpGANでは, 実データと生成データを結合し, 生成データをある実データと比較した際のリアルさによって評価します. これにより, 各実データの近傍に決定境界が維持されるので, モード崩壊を防止することができます. 先ほどの既存研究では, RpGANの損失関数の地形にはモード崩壊等に対応する局所最小値が存在せず, すべての局所最小値が大域的最小値であることが示されているようです.

Training Dynamics of RpGAN

先ほどの既存手法によって, RpGANのモード崩壊/消失への対処は可能になりました. 一方で学習ダイナミクスについては不明です. RpGANの損失関数

$$\mathcal{L}(\theta, \psi)=\mathbb{E}_{z\sim p_{z}x\sim p_{\mathcal{D}}}[f(D_{\psi}(G_{\theta}(z))-D_{\psi}(x))]$$

の最終目標は $p_{\theta^*}=p_{\mathcal{D}}$ かつ 任意の $p_{\mathcal{D}}$ 上の点で $D_{\psi^*}$ となる平衡点 $(\theta^*, \psi^*)$ を見つけることです. 先ほどの既存研究では合理的な仮定の下では損失関数の地形上で非単調増加な軌道に沿って $\theta^*$ に到達可能であることが示されているようです. しかし, 理論的に可能だからと言って実際に勾配降下によってたどり着けるかと言われるとそのようなことはありません (もちろん, たまたまたどり着くことも可能性としてはあります). RpGANはその提案論文で, 正則化を施さない場合は経験的に性能が悪いことを示しています.

命題1

正規化されていない RpGAN は、勾配降下法を用いても必ずしも収束しない。

証明を書きたいところですが, 結構長くなっているので論文のAppendix Bを参照ください.

また, RpGANは特定の種類の $p_{\mathcal{D}}$ (例えばデルタ分布に収束するものなど)に対しては収束しないです. このような分布に対しても適切に動作させるには, さらなる正則化が必要です.

著者らは勾配ペナルティを検討しました. これは, 古典的なGANでは0中心の勾配ペナルティ (0-GP)が学習の収束を促進することが知られているからです. 一般的には $R_1, R_2$ の2種類の0-GPが使われます.

$$\begin{align*} R_1(\psi)&=\frac{\gamma}{2}\mathbb{E}_{x \sim p_{\mathcal{D}}} \left[\|\nabla_x D_\psi\|^2\right] \\ R_2(\theta, \psi)&=\frac{\gamma}{2} \mathbb{E}_{x \sim p_\theta} \left[\|\nabla_x D_\psi\|^2 \right] \end{align*}$$

$R_1$ は実データ, $R_2$ は生成データ上でのDiscriminatorの勾配ノルムにペナルティをそれぞれ課します.

GANの学習ダイナミクスに関するこれまでの分析の多くは局所収束性に焦点を当てています. すなわち, $(\theta, \psi)$ が $(\theta^*, \psi^*)$ の近傍にある場合に, 学習が少なくとも収束するかどうか, ということです. このような状況においては勾配ベクトル場 $(-\nabla_\theta\mathcal{L}, \nabla_\psi\mathcal{L})$ のヤコビアンのスペクトルを調べることで収束挙動を分析できます. ここでの重要な点は, Generatorが既に真の分布を捉えている際に, $\nabla_x D=0$ としたいということです. すると, Generatorが最適な状態にとどまることができ, 学習における振動も防ぐことができます. $R_1, R_2$ は $p_\theta=p_{\mathcal{D}}$ の場合に同じ制約を課します.

ここまでは通常のGANに関する話でしたが, これはRpGANにも当てはまるので拡張できます.

命題2

$R_1$ または $R_2$ による正則化をRpGANに施すことで, 局所解に収束させることができる.

これも証明が結構長くなっているので論文のAppendix Cを参照ください.

A Practical Demonstration

先ほどの損失関数における正則化を実験的に確認します. StackedMNISTをデータセットとして用い, GeneratorとDiscriminatorには小規模なResNetを使用します. 正規化層は使いません. 事前学習したStackedMNIST分類器を使用して, $p_{\mathcal{D}}$ の1000個あるモードのうち, $p_{\theta}$ によって, 幾つが復元されたかを測定できます. また, 生成データと実データのKL reverseを用いてKLを推定します.

まずはGeneratorのlossを見てみます.

$R_1$ は理論的には収束が保証されていますが, 実験ではGAN, RpGANともに損失が大きくなっています. 一方で, $R_2$ も併用すると, 損失が損失が安定しているように見えます.

実際にモードも多様に生成されていることがわかります. ちなみに, StyleGANはminibatch standard deviation trickを導入していますがこれによってモード数は30ほど増加し881になるものの, KL reverseは変化しなかったようです.

この結果からわかるように, $R_1$ だけではGANの学習の安定性という観点から不十分です. この点についての理論的な説明は論文では与えられていません.

$(\theta, \psi)$ が $(\theta^*, \psi^*)$ に十分近いという仮定は当然ですが学習初期においては成立しません. この状況ではDiscriminatorが強力な場合, $D$ を実データに対してのみ正則化したとことで生成データに対する挙動に影響はあまりなく, その結果として生成データに対してDiscriminatorが不安定な挙動を示すと考えられます. これが原因で学習が破綻すると著者らは考えているようです. この観察結果は既存研究でも指摘されていて, $R_1$ のみでDiscriminatorを正則化すると実データを記憶することによって, 生成データに対する勾配が爆発します.

ではどうすればいいのかというと答えはシンプルで, Discriminatorを実データと生成データの両方で正則化すればいいです. $R_1$ と $R_2$ の併用によって $p_{\mathcal{D}}$ と $p_{\theta}$ の両方が平滑化され, $p_{\mathcal{D}}$ のみを平滑化する場合より学習が容易になります.

実際, 著者らの実験でも, $R_1$ と $R_2$ を併用した場合, 学習初期でも $\mathbb{E}_{x \sim p_{\mathcal{D}}} \|\nabla_x D\|^2 \approx \mathbb{E}_{x \sim p_\theta} \|\nabla_x D\|^2$ が成り立つ傾向があります. 既存研究ではこのような場合にDiscriminatorが最大マージンの分類器となることを示しています. $R_1$ と $R_2$ の片方だけでは成り立ちません.

また, 実データと生成データの勾配ノルムを同じくらいにしておくことはDiscriminatorの過学習抑制にも繋がります. 既存研究ではDiscriminatorが過学習を始めるときにはこの2つのノルムがずれ始めることも観察されています.

A Roadmap to a New Baseline — R3GAN

著者らは新しいGANのベースラインとして、R3GANを提案しています. 先ほどの著者のツイート（ポスト）のスレッドでは、DCGANと同じ扱いとしています.

R3GANはRpGANに $R_1, R_2$ を併用したものになっています. 論文ではStyleGAN2 (Config A)をベースとして共通点と相違点を示しているので, ここでもそれに沿って話を進めていきます.

ここでStyleGAN2について簡単に触れておきます. GeneratorにはVGG-likeなbackboneを, DiscriminatorにはResNetを採用し, AdaINなどを含めたいわゆる「スタイル」をベースとした生成を促進する工夫と, backboneを補強するための改良が施されています.

まず, StyleGAN2の本質的でない機能を取り除いた構成 (Config B)を構築し, そこに今回用いる損失関数を適用します (Config C). そして, VGG-likeなbackboneを新しくしていきます (Config D/E).

これらの設定について, 順々に評価をしていき, 性能を見ていきます. どの設定もはFFHQ (256x256)で評価します. GeneratorとDiscriminatorともに25Mほどのパラメータです. 学習はDiscriminatorが5Mの実画像を処理するまで行います.

Config B

StyleGAN2の画像生成に関係ない部分をすべて削ぎ落とします. 具体的には

• mapping network
• style injection
• weight modulation/demodulation
• noise injection
• mixing regularization
• path length regularization
• $z$ normalization
• mini-batch stddev
• equalized learning rate
• lazy regularization

です. また, StyleGAN-XLやStyleGAN-Tの成果をもとに, $z$ の次元は64に減らします. equalized learning rateを無くしたため, 学習率は下げる必要があり, $2.5\times10^{-3}$ から $5\times10^{-5}$ になります. 当然, 様々な工夫を廃しているので性能はConfig Aより劣りますが, ベースラインとして機能してくれます. Config BをDCGANと比較すると, 以下のような違いが挙げられます.

(a): $R_1$ 正則化による収束性のある目的関数
(b): 学習率が小さく, モーメンタムを伴う最適化手法を回避 (Adamにおける $\beta_1=0$)
(c): GeneratorおよびDiscriminatorの両方で正規化層を使わない
(d): stride付き（転置）畳み込みではなくバイリニア補間を採用
(e): GeneratorおよびDiscriminatorの両方でLeaky ReLUを使い, Generatorの出力層でtanhは使わない
(f): Generatorの入力には $4\times4$ の定数テンソルを使い, 出力スキップ接続を含むGenerator, ResNet構造のDiscriminatorを用いている

実は, (a)-(c)のいずれかを満たさない場合には学習が失敗する傾向があります. 初期のGANでうまくいっているように見えたのはGANの最適化問題の解がfull-rankであったと考えられます.

Config C

ここでは, 先ほど提案したlossを用います.

Config D

ここではアーキテクチャを近代化させます. まず, 1-3-1 bottleneck ResNetをGeneratorとDiscriminatorの両方に採用します. また, 様々な改良を施したりConvNeXtの改良手法も取り入れたりしています. 具体的には

i. 一貫して性能向上に寄与するもの
i.1): 深さ方向の畳み込みによるwidthの増加
i.2): inverted bottleneck
i.3): 活性化関数の削減
i.4): resampling層の分割
ii. 性能向上がごくわずかなもの
ii.1): チャネル数を減らした大きなカーネルの深さ方向の畳み込み
ii.2): ReLUのGELUへの置換
ii.3): 正規化層の削減
ii.4): batch normのlayer normとの入れ替え
iii. 今回の設定には無関係なもの
iii.1): 改良された訓練戦略
iii.2): stage ratio
iii.3): patchify stem

今回の論文ではi)を適用することを考えます. 特に, 古典的なResNetに対してはi.3)およびi.4)を適用し, i.1)とi.2)はConfig Eにとっておきます. ii)の要素は既存研究によると, vision transformerを模倣するためだけのもので大した性能改善にはなりません. ii.3)やii.4)は先ほどの

GeneratorおよびDiscriminatorの両方で正規化層を使わない

に反するので適用できないです.

ここまでの流れから, i.3), i.4), (c), (d), (e)を踏まえることで, StyleGAN2のbackboneを近代化されたResNetに置き換えることが可能です. GeneratorとDiscriminatorで対称的な設計を行います. パラメータ数は23.3万ほどで, StyleGAN2の24万とほぼ一致します. アーキテクチャは最小限の構成とし, 各resolution stageは1つのtransition層と2つのresidual blockから構成されます. transition層はspatial sizeおよびfeature map sizeの変更のためにバイリニアリサンプリングと1つの$1\times1$ 畳み込み (optional)で構成されます. Residual blockはConv$1\times1$ → Leaky ReLU → Conv$3\times3$ → Leaky ReLU → Conv$1\times1$ の5処理です. 最後の畳み込み層はbiasなしです.

初期化はFix-upを採用します. Residual blockでは最後の畳み込みは0で初期化, 残りはscale $L^{-0.25}$ で縮小します. $L$ はResidual blockの数です. Fix-upはここでのみ採用し, 残りの工夫は使いません.

Config E

Residual blockは i.1)を適用するために $3\times3$ の部分をGroup Convに置き換えます. Group sizeは16で, ConvNeXt (group size 1)とは異なる点に注意が必要です. ConvNeXtの設定がGPU上では非効率で高速化が期待できないためとされています. Group Convにすることでモデルサイズを維持しつつbottleneckの圧縮率を2に下げることができます. これによってbottleneckのwidthはConfig Aと比較すると1.5倍になります. Group Convの計算コストが $1\times1$ の畳み込みと比較して非常に小さいのでここの容量を高めるためにi.2)を適用します. bottleneck widthとstem widthを反転させることでモデルサイズは増えずに幅を倍にできます.

文字ばかりで想像が難しいと思うので

にその概要図を示します.

いままでの設定をFFHQ-256で比較すると以下のようになります.

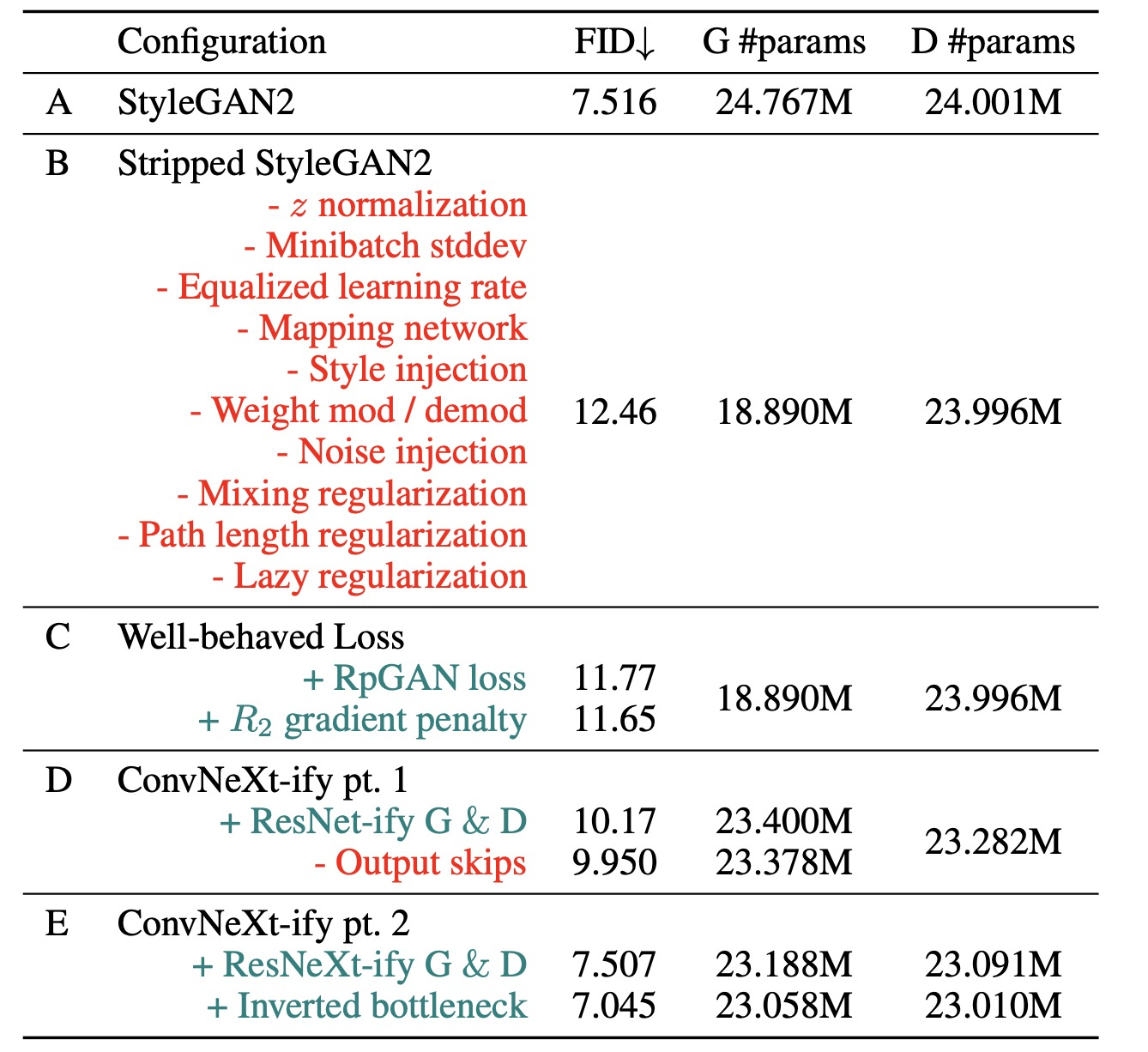
最終的にはStyleGAN2を上回っています.

実験

GANにはモード崩壊がつきものです. まずはStackedMNISTを使って性能を確認します.

これはunconditionalな設定ですが, 1000クラスの生成が確認できます. これ以上のことは書かれていませんが, 個人的にはconditionalな設定や解像度を上げた設定でもやってほしいなと思いました.

続いて, FFHQ-256でFIDでの比較をしてみます.

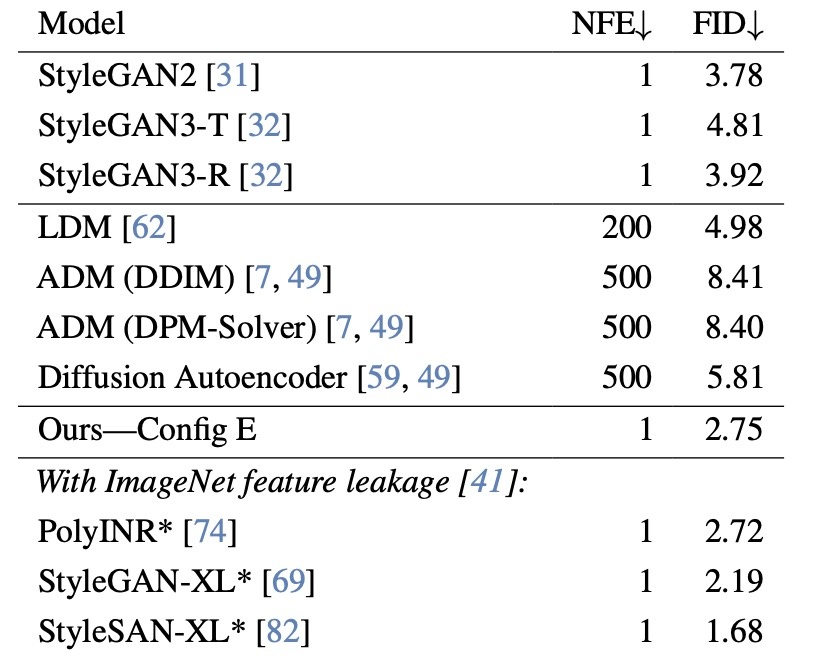
提案手法より低いFIDの手法はImageNetの特徴抽出のようなことをしていたりするのでleak扱いされているようです. そのImageNetのFIDでは $32\times32$ と $64\times64$ ではありますが, leakなしの条件で拡散モデルを上回る性能を示しています ($32\times32$ はconditionalな生成). パラメータ数も拡散モデルベースのものの30%ほどです.

limitations

ここまでの話の流れから明らかですが, この研究はGANで必要な最小構成要素を見つけることを主眼に置いています. たとえば, StyleGAN系統では必須のstyle injectionの機能がなかったりします. そのため, 画像の生成はうまくいっているが, 編集や制御には適していないです. 実際, 著者らも論文でそのように述べているほか, twitterでも

https://x.com/SkyLi0n/status/1877824432091332828

Think of it as DCGAN in 2025 rather than something feature-rich like StyleGAN.

と述べており, これをベースにして今後の研究を発展させたいと考えているようです.

思ったこと

• GANの研究はアーキテクチャがベースはそのままに魔改造されていた印象を自分は受けていたので一旦ここでリセットするのは良さそうに思えます (拡散モデル, またはrectified flowでも最近はごちゃごちゃし始めている感じがあります).

• 実は実験設定が結構シンドイです. これまでは述べなかったのですが, 今回の実験でのハイパーパラメータはデータセットや解像度で異なっており, 以下のようになっています. これがなくなると最高ですが...

  

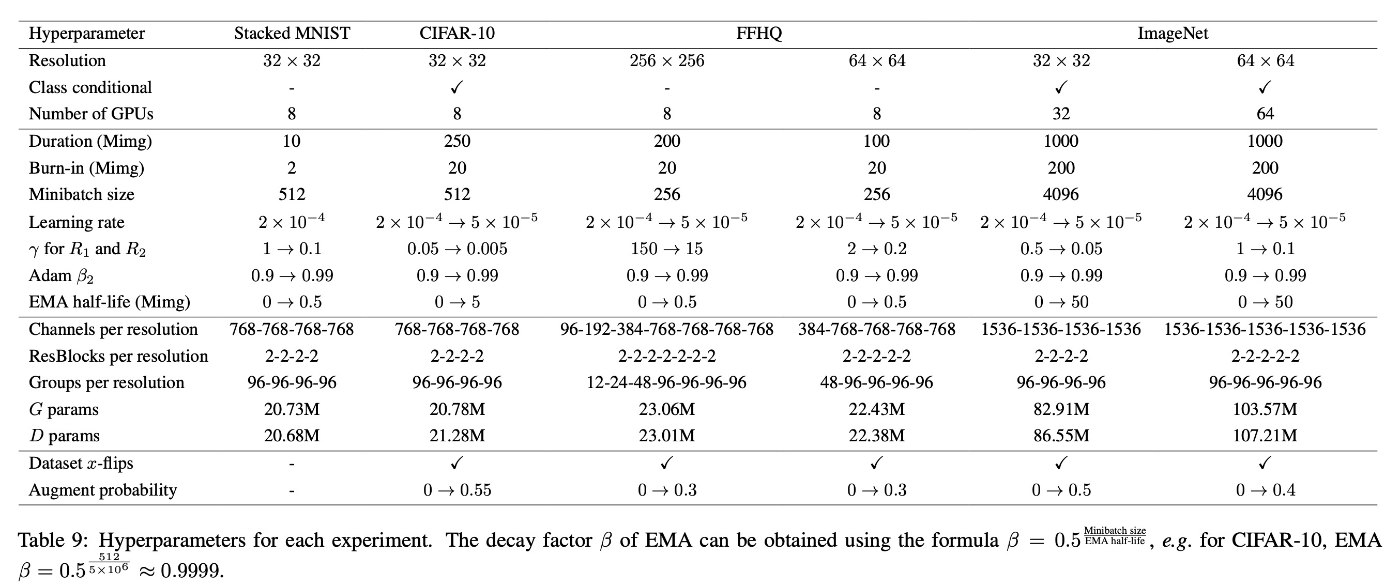
• Transformerでの結果が気になります. GANでももちろんTransformerを使ったモデルがありますし (TransGANなど), 画像認識と同じでどっちがいいのか状態になるのかなという気がします. ちなみに査読でも指摘されていて

  We have not conducted any experiments, but are also interested to see how they perform. In particular, whether adding attention blocks to a ConvNet (similar to BigGAN and diffusion UNet) or using a pure transformer architecture (similar to DiT) will result in stronger performance. Given the impressive results of EDM2 (which uses UNet), it seems the argument has not yet settled for generative modeling.

  と返しているので気になります.

参考文献

• Nick Huang, Aaron Gokaslan, Volodymyr Kuleshov, and James Tompkin. The GAN is dead; long live the GAN! a modern GAN baseline. In The Thirty-eighth Annual Conference on Neural Information Processing Systems, 2024.
• Alexia Jolicoeur-Martineau. The relativistic discriminator: a key element missing from standard gan, 2018.
• Andrew Melnik, Maksim Miasayedzenkau, Dzianis Makaravets, Dzianis irshtuk, Eren Akbulut, Dennis Holzmann, Tarek Renusch, Gustav Reichert, and Helge Ritter. Face Generation and Editing With StyleGAN: A Survey . IEEE ransactions on Pattern Analysis & Machine Intelligence, 46(05):3557–3576, May 2024.
• Axel Sauer, Tero Karras, Samuli Laine, Andreas Geiger, and Timo Aila. StyleGAN-t: Unlocking the power of GANs for fast large-scale text-to-image synthesis. In Andreas Krause, Emma Brunskill, Kyunghyun Cho, Barbara Engelhardt, Sivan Sabato, and Jonathan Scarlett, editors, Proceedings of the 40th International Conference on Machine Learning, volume 202 of Proceedings of Machine Learning Research, pages 30105–30118. PMLR, 23–29 Jul 2023.
• Ruoyu Sun, Tiantian Fang, and Alexander Schwing. Towards a better global loss landscape of gans. In H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan, and H. Lin, editors, Advances in Neural Information Processing Systems, volume 33, pages 10186–10198. Curran Associates, Inc., 2020.