Rectified Flow①

以下の2つの論文

https://openreview.net/forum?id=XVjTT1nw5z

https://openreview.net/forum?id=mSHs6C7Nfa

を読みたいのですが, まとめると長くなりすぎるのでいくつかに分けます (お気持ちだけの話なら長くはならないですが, それは日本語でまとめる意味もなさそうです). まずはベースとなっている1つ目の論文の最初の方を読みます. 若干式変形がわからず, 論文の式変形をそのまま載せています.

書籍情報

参考文献も同様です

Xingchao Liu, Chengyue Gong, and Qiang Liu. Flow straight and fast: Learning to generate and transfer data with rectified flow. The Eleventh International Conference on Learning Representations, 2023

関連リンク

• OpenReview
• arXiv
• 公式実装
• 公式blog？のようなもの

概要

Rectified Flowは色々な見方をすることができるのですが, 論文に則って進みます. Rectified FlowはTransport Mapping Problemを解くためのアプローチです.

$\mathbb{R}^d$ 上の2つの分布のemprical observation $X_{0}\sim\pi_{0}, X_{1}\sim\pi_{1}$ が与えられ, $Z_{0}\sim\pi_{0}$ の状況において, $Z_{1}\coloneqq T(Z_{0})\sim\pi_{1}$ を満たすような transport map $T:\mathbb{R}^d\rightarrow\mathbb{R}^d$ を見つける問題.

ここでは, $(Z_0, Z_1)$ を $\pi_0, \pi_1$ のカップリングと呼びます.

例えば生成タスクであったら $\pi_0$ が正規分布のような単純なもので, $\pi_1$ がデータ分布となります (逆でも問題ないです). いままでもこの変換 $T$ については研究されていますが, いろいろ欠点があったりします (例としてモード崩壊や何度も推論が必要なことなどが挙げられます). Rectified Flowは非常にシンプルでL2 normの最小化によって学習されるので, 非常にシンプルです. また,

1. 全ての凸コスト (convex cost) $c$ に対して輸送コストが共同して増加しないカップリングが得られる
2. flowがどんどん直線になるので数値解法による誤差が少なくなる

などの利点があります. まずは実際に結果を見てみます.

https://www.cs.utexas.edu/~lqiang/rectflow/html/intro.html より引用

$\pi_{0}$ として上2段では標準正規分布, 下2段ではhuman facesの分布が, 同様に $\pi_{1}$ としてはcat facesが用いられています. 1-Rectified FlowとはReflowをしていないモデルですが, それでもstepsの少ない段階からcat facesが確認できます. Reflowを1回行った2-Rectified Flowでは $N=1$ の段階でcat facesが確認でき, より少ない回数での推論が可能になっていることがわかります.

ちなみに最近の拡散モデルとの関連では, 解軌道が直線的になることが挙げられます.　ちなみに, flow-basedな生成モデルだと, 関数 $f(x)$ が可逆であることを要求しますがここではそのようなことを陽に要求しません. 実際には $\pi_0, \pi_1$ をスワップすることで (数式的には)実現可能です. これは後で登場する目的関数が時間対称であるため, 逆方向のプロセスも同等に重視されるためです (と, 私は解釈しています).

Method

手法の細かい部分に入ります. まずは概要をさらって, その後理論の話に入っていきます.

Overview

Rectified Flow

まず, 結論を述べます. emprical observation $X_{0}\sim\pi_{0}, X_{1}\sim\pi_{1}$ が与えられたとき, $(X_0, X_1)$ から誘発された (論文ではinducedが使われています) rectified flowは時刻 $t\in[0, 1]$ に対するODEモデル

$$\mathrm{d}Z_t=v(Z_t, t)\mathrm{d}t$$

です. これは, $\pi_0$ からサンプリングされた $Z_0$ を $\pi_1$ に従う $Z_1$ に変換します. $v:\mathbb{R}^d\to\mathbb{R}^d$ はdrift forceで, フローが $X_0$ から $X_1$ への直線経路の方向 $(X_1-X_0)$ にできるだけ従うように設定されます. より厳密には, 経路ごとに連続的に微分可能なrandom process $\boldsymbol{X}=\{X_t:t\in[0,1]\}$ に対する期待速度 (expected velocity) $v^{\boldsymbol{X}}$ を

$$v^{\boldsymbol{X}}(x, t)=\mathbb{E}[\dot{X}_t\mid X_t=x]\quad \forall x\in\mathrm{supp}(X_t)$$

で定義します. ちなみに, $x\not\in\mathrm{supp}(X_t)$ に対しては条件付き期待値を計算できないので $v^{\boldsymbol{X}}=0$ とします.

$v$ は以下のシンプルな回帰問題を解くことで得られます.

$$\min_{v}\int_0^1\mathbb{E}\left[\|(X_1-X_0)-v(X_t, t)\|^2\right]\,\mathrm{d}t$$

ここで, $X_t=tX_1+(1-t)X_0$ で, $X_0$ と $X_1$ の線形補間です. 素朴に考えると $X_t$ はODE $\mathrm{d}X_t=(X_1-X_0)\mathrm{d}t$ に従うのでこれを解けばいいですが, 実際にはかなり難しい (というか多分解けない)です. それは, 推論時には $X_1$ がわからないからです. drift $v$ を $X_1-X_0$ に合わせることでrectified flowは線形補間 $X_t$ の経路を因果化 (causalize) し, 未来の情報を参照せずにシミュレーション可能なODEフローを生成することができます.

実装上は, $v$ をニューラルネットワークなどでパラメータ化します. アルゴリズムは以下の通りです.

$v$ が得られたら, ODEを解きます. 逆方向のサンプリングでは, $\tilde{X}_0\sim\pi_1$ で初期化し, $\mathrm{d}\tilde{X}_t=-v(\tilde{X}_t, t)\mathrm{d}t$ を解き, $X_t=\tilde{X}_{1-t}$ とします. 逆方向でも順方向でも訓練のアルゴリズムは同じです. それは, 先ほど設定した回帰問題が時間対称なのでどちらの方向も同じ問題として扱えるためです.

なお, お気持ちベースでは, 直線軌道にすると説明されたりしますが, そのためにはAlgorithm 1のOptionalにあるReflowが必要です. Reflowを何回か行うと軌道がほぼ直線的になり, $Z_1=Z_0+v(Z_0, 0)$ で求めることができます. これは $Z_1=Z_0+v(Z_0, 0)\cdot(1-0)$ なので, $v(Z_0, 0)$ は $Z_0$ と $Z_1$ を結ぶ線分の傾きと見ることもできます.

Flows avoid crossing

大事なポイントとして, フローが非交差という特性を持つという点です. well definedなODE $\mathrm{d}Z_t=v(Z_t, t)\mathrm{d}t$ に従う異なる経路は, 解が一意に存在する場合は任意の時刻 $t\in[0, 1]$ で互いに交差しません.

具体的には, ある位置 $z\in\mathbb{R}^d$ と時刻 $t\in[0, 1]$ において, 2つの経路が異なる方向に沿って $z$ を通過することはないです. 通過してしまうと, ODEの解が複数存在することになり, 一意性が失われます. 一方で, 補間過程 $X_t$ のある2つの経路は $(X_0, X_1)$ の値によって交差する可能性があります. これは下図の(a)の状況です. そのため, rectified flowでは(b)のように軌跡を再配線して交差を回避します.

Rectified flows reduce transport costs

目的の式が正確に解かれた場合, rectfied flow のペア $(Z_0, Z_1)$ は $\pi_0$ と $\pi_1$ のvalid couplingであることが保証されます. すなわち, $Z_0\sim\pi_0$ のとき $Z_1$ は $\pi_1$ に従います.

さらに, $(Z_0, Z_1)$ は全ての凸コスト関数 $c$ に対してデータペア $(X_0, X_1)$ よりも大きくない輸送コストであることが保証されます. データペア $(X_0, X_1)$ は $\pi_0, \pi_1$ の任意のカップリングであり, 通常は独立です ($(X_0, X_1)\sim\pi_0\times\pi_1$). これは実際の問題では対応関係が観測できないことによります. 一方で, rectified カップリング $(Z_0, Z_1)$ はODEモデルによって構築されるので決定論的な依存性を持っています. $(X_0, X_1)$ から $(Z_0, Z_1)$ へのマッピングを $(Z_0, Z_1)=\mathtt{Rectify}((X_0, X_1))$ と表します. このように, $\mathtt{Rectify}(\cdot)$ は任意のカップリングをより小さい凸輸送コストを持つ決定論的なカップリングに変換します.

Straight line flows yield fast simulation

rectified flowのアルゴリズムに従って, $(X_0, X_1)$ から誘発されるrectified flowを $\mathtt{Rectify}((X_0, X_1))$ と表します. この演算子を再起的に適用することで, $(Z_0^0,Z_1^0)=(X_0, X_1)$ を初期条件として $\boldsymbol{Z}^{k+1}=\mathtt{RectFlow}((Z_0^k, Z_1^k))$ というrectified flowの列ができます. $\boldsymbol{Z}^{k}$ を $(X_0, X_1)$ から誘発された $k-$th rectified flowまたは $k-$rectified flowと呼びます.

先ほどの図(b)では, rectified flowをしただけでは直線軌道にならず, 折れ曲がっていることがわかります. このreflowという過程は, 輸送コストを削減するだけでなく, 経路をより直線軌道にするという効果もあります.

これで何が嬉しいかというと, ほぼ直線軌道の経路を持つ場合は数値シミュレーションによる時間離散化誤差が小さくなります. 完全な直線経路の場合は単一のEuler stepでシミュレーションできるので, one-stepなモデルになります. 生成モデルで言えばone-step生成が可能になるということです.

Main Results and Properties

いくつかの性質を確認します.

Marginal preserving property

これは, Overviewで見た

目的の式が正確に解かれた場合, rectfied flow のペア $(Z_0, Z_1)$ は $\pi_0$ と $\pi_1$ のvalid couplingであることが保証されます. すなわち, $Z_0\sim\pi_0$ のとき $Z_1$ は $\pi_1$ に従います.

という性質です. 論文中では定理3.3となっており, 書き下すと以下のようになります.

$\boldsymbol{X}$ をrectifiableとし, $\boldsymbol{Z}$ をそのrectified flowとする. すると, $\forall t\in[0, 1], \mathrm{Law}(Z_t)=\mathrm{Law}(X_t)$

$\boldsymbol{X}$ がrectifiableであるとは, $v^{\boldsymbol{X}}$ が局所的に有界 (locally bounded)で, 以下の積分方程式の解が存在し, かつ一意であることを満たしていることを言います.

$$Z_t=Z_0+\int_{0}^{t}v^{\boldsymbol{X}}(Z_t, t)\,\mathrm{d}t\quad \forall t\in[0, 1],\quad Z_0=X_0$$

この場合, $\boldsymbol{Z}=\{Z_t: t\in[0,1]\}$ は $\boldsymbol{X}$ に誘発されたrectified flowであると言います.

さて, 上の定理3.3を証明します. Lawとは確率分布のことらしいです.

任意のcompactly supportedな連続で微分可能なテスト関数 $h:\mathbb{R}^d\rightarrow\mathbb{R}$ に対し,

$$\dfrac{\mathrm{d}}{\mathrm{d}t}\mathbb{E}[h(X_t)]=\mathbb{E}[\nabla h(X_t)^\top\dot{X_t}]=\mathbb{E}[\nabla h(X_t)^\top v^{\boldsymbol{X}}(X_t, t)]$$

です. ここで, $\dfrac{\mathrm{d}}{\mathrm{d}t}\mathbb{E}[h(X_t)]=\mathbb{E}[\nabla h(X_t)^\top\dot{X_t}]$ では期待値と微分の順序交換, $\mathbb{E}[\nabla h(X_t)^\top\dot{X_t}]=\mathbb{E}[\nabla h(X_t)^\top v^{\boldsymbol{X}}(X_t, t)]$ では$v^{\boldsymbol{X}}(X_t, t)=\mathbb{E}[\dot{X}_t|X_t]$ であることを使っています.

これは, $\pi_t\coloneqq\mathrm{Law}(X_t)$ がdrift $v_t^{\boldsymbol{X}}\coloneqq v^{\boldsymbol{X}}(\cdot,t)$ を持つ連続方程式を解くことと同値らしいです.

$$\dot{\pi_t}+\nabla\cdot(v_t^{\boldsymbol{X}}\pi_t)=0$$

この式に $h$ をかけて積分すると

$$0=\int h(\dot{\pi_t}+\nabla\cdot(v_t^{\boldsymbol{X}}\pi_t))=\int h\dot{\pi_t}-\nabla h\top v_t^{\boldsymbol{X}}\pi_t=\dfrac{\mathrm{d}}{\mathrm{d}t}\mathbb{E}[h(X_t)]-\mathbb{E}[\nabla h(X_t)^\top v^{\boldsymbol{X}}(X_t, t)]$$

です. ここで, $\int h\nabla\cdot(v_t^{\boldsymbol{X}}\pi_t)=-\int\nabla h^\top(v_t^{\boldsymbol{X}}\pi_t)$ を使っています.

さて, $Z_t$ は同じ速度場 $v^{\boldsymbol{X}}$ によって運ばれます. すなわち, $Z_t$ の周辺分布 (marginal law) $\mathrm{Law}(Z_t)$ は初期値 $Z_0=X_0$ のときのものと同じです. したがって,

$$\dot{\pi_t}+\nabla\cdot(v_t^{\boldsymbol{X}}\pi_t)=0$$

の解が一意であることは $\mathrm{d}Z_{t}=v^{\boldsymbol{X}}(Z_{t}, t)\mathrm{d}t$ の等価性と一致します. すると $\mathrm{Law}(Z_t)$ と $\mathrm{Law}(X_t)$ の等価性が成り立ちます.

reference

rectified flowの論文では, 以下の2つがこのことのreferenceとして挙げられています.
Thomas G Kurtz. Equivalence of stochastic equations and martingale problems. In Stochastic analysis 2010, pages 113–130. Springer, 2011.
https://link.springer.com/chapter/10.1007/978-3-642-15358-7_6

Luigi Ambrosio and Gianluca Crippa. Existence, uniqueness, stability and differentiability properties of the flow associated to weakly differentiable vector fields. In Transport equations and multi-D hyperbolic conservation laws, pages 3–57. Springer, 2008.
https://link.springer.com/chapter/10.1007/978-3-540-76781-7_1

Reducing trasport costs

これは

$(Z_0, Z_1)$ は全ての凸コスト関数 $c$ に対してデータペア $(X_0, X_1)$ よりも大きくない輸送コストであることが保証されます.

という性質です. 論文中では定理3.5となっており, 書き下すと以下のようになります.

$(X_0, X_1)$ をrectifiable, $(Z_0, Z_1)=\mathtt{Rectify}((X_0, X_1))$ とする. 任意の凸コスト関数 $c:\mathbb{R}^d\rightarrow\mathbb{R}$ に対して$\mathbb{E}[c(Z_1-Z_0)]\leq\mathbb{E}[c(X_1-X_0)]$.

これを示します. Jensenの不等式を2回用いると示されます.

$$\begin{align*} \mathbb{E}[c(Z_1-Z_0)]&=\mathbb{E}\left[c\left(\int_0^1v^{\boldsymbol{X}}(Z_t, t)\,\mathrm{d}t\right)\right] \quad (\because \mathrm{d}Z_t=v^{\boldsymbol{X}}(Z_t, t)) \\ &\leq \mathbb{E}\left[\int_0^1c\left(v^{\boldsymbol{X}}(Z_t, t)\right)\,\mathrm{d}t\right] \quad (\because c\mathrm{は凸関数でJensenの不等式}) \\ &=\mathbb{E}\left[\int_{0}^{1}c\left(v^{\boldsymbol{X}}(X_t, t)\right)\,\mathrm{d}t\right] \quad (\because X_t\mathrm{と}Z_t\mathrm{は同じ周辺分布を持つ}) \\ &=\mathbb{E}\left[\int_{0}^{1}c(\mathbb{E}[(X_1-X_0)\mid X_t])\,\mathrm{d}t\right] \quad (\because v^{\boldsymbol{X}}\mathrm{の定義}) \\ &\leq\mathbb{E}\left[\int_{0}^{1}\mathbb{E}[c(X_1-X_0)\mid X_t]\,\mathrm{d}t\right] \quad (\because c\mathrm{は凸関数でJensenの不等式}) \\ &=\int_{0}^{1}\mathbb{E}[c(X_1-X_0)]\mathrm{d}t \quad (\because \mathbb{E}[\mathbb{E}[(X_1-X_0)|X_t]]=\mathbb{E}[(X_1-X_0)]) \\ &=\mathbb{E}[c(X_1-X_0)] \end{align*}$$

Reflow, straightening, fast simulation

toy dataを使って, $\boldsymbol{Z}^{k+1}=\mathtt{RectFlow}((Z_0^k, Z_1^k))$ を繰り返し適用することで, $k-$th rectified flow $\boldsymbol{Z}^k$ のパスが直線的になることを確認します.

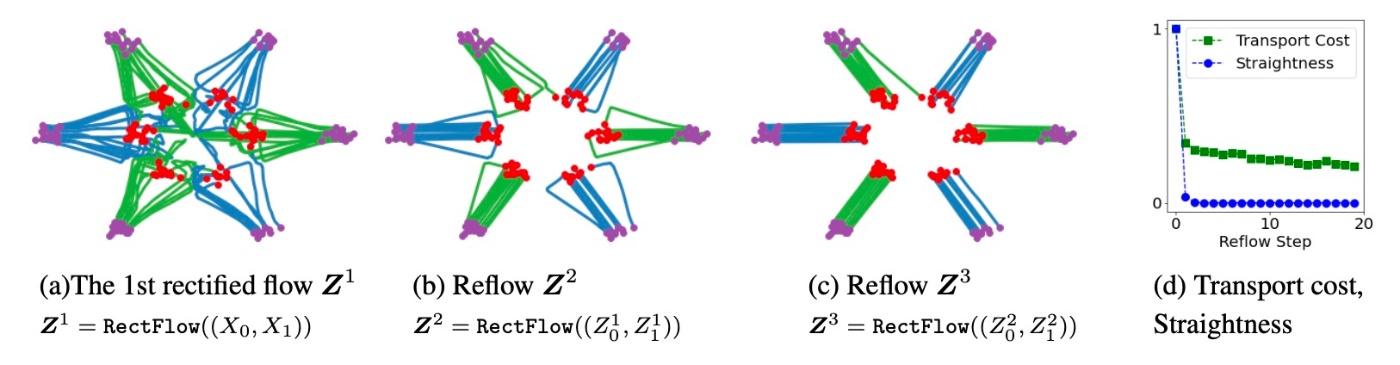
図を見ると, (a)から(c)にかけて軌道が直線的になっていることがわかります. また, (d)からtransport costやstraightnessがReflowを行うことで減少することもわかります. ここでは, このことを理論的に保証します.

具体的には, flow $\mathrm{d}Z_t=v(Z_t, t)\mathrm{d}t$ が直線的 (straight)であるとは, 任意の $t\in[0, 1]$ に対してほぼ確実に $Z_t=tZ_1+(1-t)Z_0$ が成り立つか, 各経路に沿って $v(Z_t, t)=Z_1-Z_0=const$ であることを指します. より正確には, 「直線的である」とは一定速度での直線を指します. このような直線的なフローは1-step inferenceが可能で, $Z_1=Z_0+v(Z_0, 0)$ で推論できてとても魅力的です. しかし, flow $\mathrm{d}Z_t=v(Z_t, t)\mathrm{d}t$ を直線的にするのは非自明な問題です. なぜかというと, $v$ はinviscid Burgers’ equation $\partial_{t}v+(\partial_{z}v)v=0$ を満たす必要があります (これを満たさなければならない理由はよくわかりませんでしたが, 以下の式変形により速度が一定であることと等価です).

$$\dfrac{\mathrm{d}}{\mathrm{d}t}v(Z_t, t)=\partial_{z}v(Z_t, t)\dot{Z}_t+\partial_{t}v(Z_t, t)=\partial_{z}v(Z_t, t)v(Z_t, t)+\partial_{t}v(Z_t, t)=0$$

より一般的には, straightnessを

$$S(\boldsymbol{Z})=\int_{0}^{1}\mathbb{E}\left[\|(Z_1-Z_0)-\dot{Z}_t\|^2\right]\mathrm{d}t$$

で測ることができ, これが0だと完全な直線と見做せます. Reflowを行うことで軌道が直線的になるとは, rectified flowの操作を再起的に行うことで $S(\boldsymbol{Z})=0$ に近づけられるということです.

論文中では定理3.7となっており, 以下のようになります.

$\boldsymbol{Z}^k$ を $(X_0, X_1)$ の $k$-th rectified flowとする. すなわち$\boldsymbol{Z}^{k+1}=\mathtt{RectFlow}((Z_0^k, Z_1^k))$　かつ $(Z_0^0, Z_1^0)=(X_0, X_1)$ である. $k=0, \ldots, K$ に対して $(Z_0^k, Z_1^k)$ がrectifiableとすると
$\displaystyle\sum_{k=0}^KS(\boldsymbol{Z}^{k+1})+V((Z_0^k, Z_1^k))\leq\mathbb{E}\left[\|X_1-X_0\|^2\right]$
また, $\mathbb{E}\left[\|X_1-X_0\|^2\right]<+\infty$ のとき, $\min_{k\leq K}(S(\boldsymbol{Z}^k)+V(Z_0^k, Z_1^k))=\mathcal{O}(1/K)$

OpenReviewのRebuttalを見ると, $\min_{k\leq K}S(\boldsymbol{Z}^k)=\mathcal{O}(1/K)$ です.

$K$ はrectified flowの操作を行う回数ですので, 理論上は無限回行うことで完全な直線になることがわかります. なお,

$$V((X_0, X_1))\coloneqq\int_{0}^{1}\mathbb{E}\left[\|(X_1-X_0)-\mathbb{E}[X_1-X_0\mid X_t]\|^2\right]\mathrm{d}t$$

です. 先ほどの定理3.7を示してみます. 定理3.5において $c(x)=\|x\|^2$ とします. すると

$$\mathbb{E}[\|X_1-X_0\|^2]-\mathbb{E}[\|Z_1-Z_0\|^2]=S(\boldsymbol{Z})+V((X_0, X_1))$$

です (論文では1次式になっていますが直前直後の流れから誤植と思われます). 同様に, 各 $k$ において

$$\mathbb{E}[\|Z_1^k-Z_0^k\|^2]-\mathbb{E}[\|Z_1^{k+1}-Z_0^{k+1}\|^2]= S(\boldsymbol{Z}^{k+1})+V((Z_0^k, Z_1^k))$$

です. $k=0, \ldots, K$ に対してtelescoping sumを取ります. すると打ち消し合いが発生し,

$$\mathbb{E}[\|X_1-X_0\|^2]-\mathbb{E}[\|Z_1^{K+1}-Z_0^{K+1}\|^2]=\sum_{k=0}^KS(\boldsymbol{Z}^{k+1})+V((Z_0^k, Z_1^k))$$

です. $\mathbb{E}[\|Z_1^{k+1}-Z_0^{k+1}\|^2]\geq0$ ですので,

$$\mathbb{E}[\|X_1-X_0\|^2]-\mathbb{E}[\|Z_1^{k+1}-Z_0^{k+1}\|^2]\leq\mathbb{E}[\|X_1-X_0\|^2]$$

となり, 示したかった不等式が従います.

おわりに

今回は12000字くらい書いたのでここで終わりにします. arXiv版の論文では, 1-8ページ上段および12ページ下段-15ページ中段までに相当する内容です.