😽

拡散モデルと表データ生成④：【論文】TabSyn

2024/03/19に公開

機械学習

Mixed-Type Tabular Data Synthesis with Score-based Diffusion in Latent Space (ICLR2024)

ICLR2024のoral採択の論文です. 自分の知る限りでは, アーキテクチャなどのレベルで拡散モデルを使って表データ生成をする論文はこれで最後になります (2024/03/18現在).

今回はarXivのversion 1を読んだまとめですが, 一部ICLRの査読やcamera-readyの内容も反映しています. 断りのない限り, 図や表は論文からの引用になります.

書籍情報

Hengrui Zhang and Jiani Zhang and Zhengyuan Shen and Balasubramaniam Srinivasan and Xiao Qin and Christos Faloutsos and Huzefa Rangwala and George Karypis. Mixed-Type Tabular Data Synthesis with Score-based Diffusion in Latent Space. The Twelfth International Conference on Learning Representations, 2024

TL;DR

Latent Diffusion Modelsを使用した表データ生成手法のTabSynの提案
生成品質, 汎用性, スピードの3つの面で既存手法を上回る結果
追加訓練なしで欠損値補完にも適用し, XGBoostと同等の性能を達成

さまざまな指標で既存手法を上回ることがわかります.

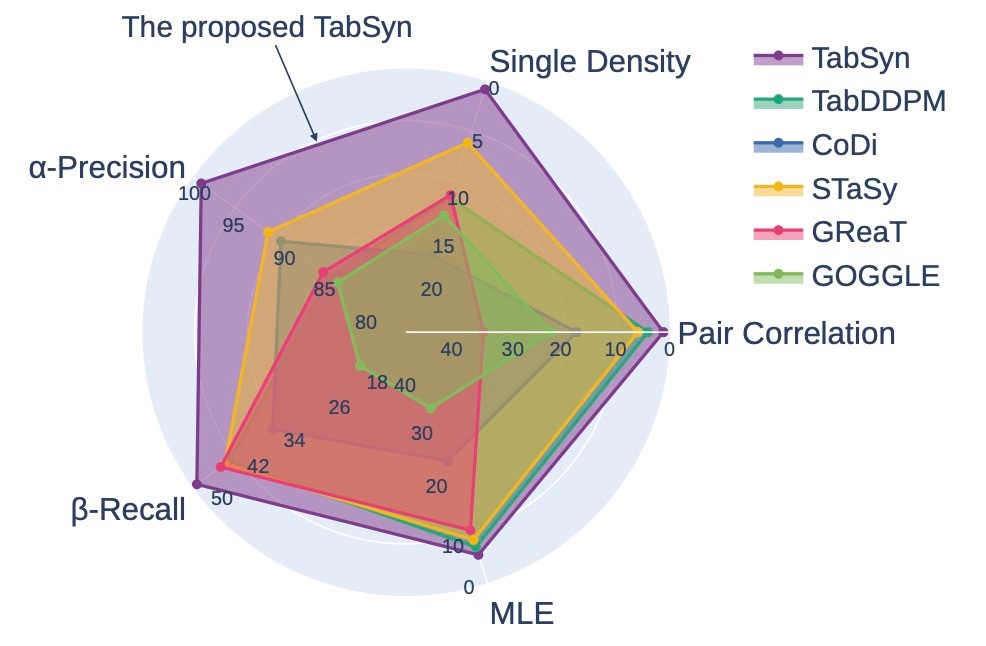
提案手法: TabSyn

まずはモデルの概要図を示します. これを見ると一目瞭然です.

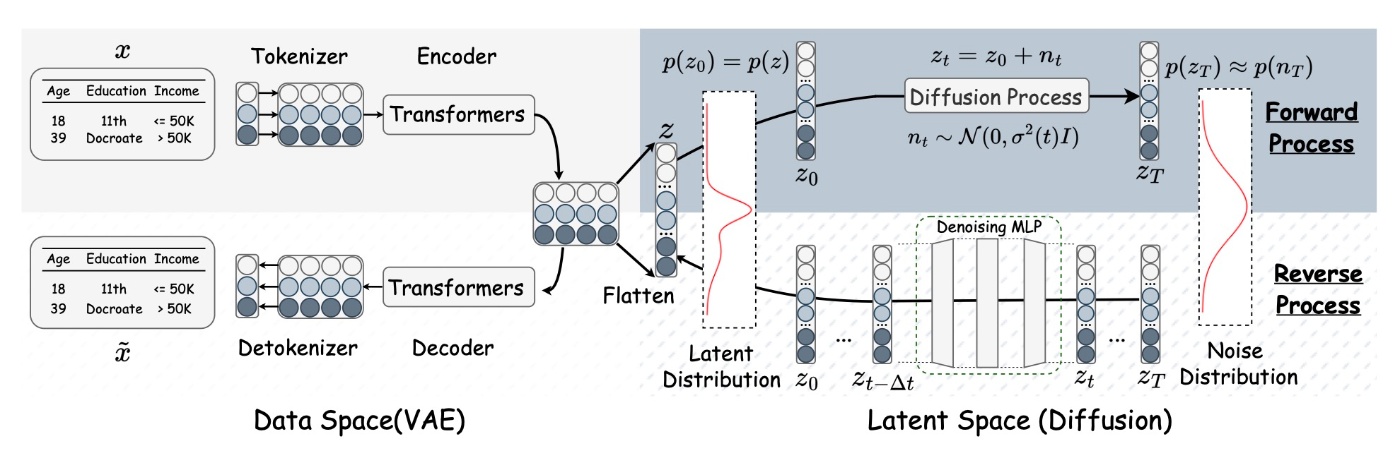
画像生成ではLatent Diffusion Models (LDM)が台頭して久しいです. Stable Diffusionの登場により多くの人が触れるようになりました.

LDMの概要自体は様々な解説記事があるので省略します. Stable Diffusionとは異なり, 基盤モデルではないのでデータセット毎に訓練する必要がある点には注意が必要です.

問題定義

TabSynの中身に入る前に記号の定義などを行います. まず, $M=M_{\mathrm{num}}+M_{\mathrm{cat}}$ のカラムを持つ表データを考えます. 各列は $\boldsymbol{x}=[\boldsymbol{x}^{\mathrm{num}}, \boldsymbol{x}^{\mathrm{cat}}]$ で表されています. もちろん $\boldsymbol{x}^{\mathrm{num}}\in\mathbb{R}^{M_{\mathrm{num}}}, \boldsymbol{x}^{\mathrm{cat}}\in\mathbb{R}^{M_{\mathrm{cat}}}$ です. 特に, $i$ 番目のカテゴリデータは $C_i$ 個の値を持ちます. すなわち $x_{i}^{\mathrm{cat}}\in\{1, \ldots,C_i\}$ です.

この論文では条件無し生成に着目します. 表データ $\mathcal{T}=\{\boldsymbol{x}\}$ があったとき, $p_{\theta}(\mathcal{T})$ をパラメータ化することが目標です.

AutoEncoder

さて, TabSynの構成要素に注目していきます. LDMはAutoEncoderとdiffusion modelsの2つから主に成り立っていますが, まずはAutoEncoderについて触れます.

表データは非常に構造化されたデータで, 各値に意味があります. 例えば画像ではピクセル値が1違っても大きな問題ありませんが, 自然言語ではトークンの値が1違うと意味が大きく変化する場合があります. また, 各カラムが密接に関連しているだけでなく, その関連度合いも異なります. 例えば都道府県と県庁所在地は一対一対応しています. しかし, 体重と身長などという場合は大まかな関連は考えられますが, この2つを明確に対応づけることは難しいです. これらの特性を加味してAutoEncoderの設計が必要になります. ここではTransformerを用いた表データ分析での成功例に倣って2つのステップを踏むことにします.

各カラムに対してunique tokenizerを学習する
token (column)-wiseな関係を学習する

Feature Tokenizer

Feature Tokenizerは各カラムを $d$ 次元のベクトルに変換します. まず, カテゴリデータはone-hot encodingを施します. すなわち, $x_{i}^{\mathrm{cat}}\Rightarrow\boldsymbol{x}_{i}^{\mathrm{oh}}\in\mathbb{R}^{1\times C_i}$ です. これによって各列は $\boldsymbol{x}=[\boldsymbol{x}^{\mathrm{num}}, \boldsymbol{x}_1^{\mathrm{oh}}, \ldots, \boldsymbol{x}_{M_{\mathrm{cat}}}^{\mathrm{oh}}]\in\mathbb{R}^{M_{\mathrm{num}}+\sum_{i=1}^{M_{\mathrm{cat}}}C_i}$ となります. その後, 数値データに線形変換を施し, カテゴリデータに対してはembedding lookup tableを作成します. これにより, ベクトルに変換されます. すなわち,

\boldsymbol{e}_i^{\mathrm{num}}=x_i^{\mathrm{num}}\cdot\boldsymbol{w}_i^{\mathrm{num}}+\boldsymbol{b}_i^{\mathrm{num}}, \quad \boldsymbol{e}_i^{\mathrm{cat}}=\boldsymbol{x}_i^{\mathrm{oh}}\cdot\boldsymbol{W}_i^{\mathrm{cat}}+\boldsymbol{b}_i^{\mathrm{cat}}

です. ここで, $\boldsymbol{w}_{i}^{\mathrm{num}}, \boldsymbol{b}_{i}^{\mathrm{num}}, \boldsymbol{b}_{i}^{\mathrm{cat}}\in\mathbb{R}^{1\times d}, \boldsymbol{W}_{i}^{\mathrm{cat}}\in\mathbb{R}^{C_i\times d}$ はtokenizerの学習パラメータで, $\boldsymbol{e}_{i}^{\mathrm{num}}, \boldsymbol{e}_{i}^{\mathrm{cat}}\in\mathbb{R}^{1\times d}$ は埋め込み表現になります. 実際の表データにはカラムがたくさんあるので, それぞれのレコードに対してそれらをスタックします.

\boldsymbol{E}=[\boldsymbol{e}_{1}^{\mathrm{num}}, \ldots,\boldsymbol{e}_{M_{\mathrm{num}}}^{\mathrm{num}}, \boldsymbol{e}_{1}^{\mathrm{cat}},\ldots,\boldsymbol{e}_{M_{\mathrm{cat}}}^{\mathrm{cat}}]\in\mathbb{R}^{M\times d}

これによって $M_{\mathrm{num}}+\sum_{i=1}^{M_{\mathrm{cat}}}C_i$ 次元のレコードが $M\times d$ 次元になりました. 公式実装および論文内の実験では, $d=4$ を採用しています.

Transformer Encoding and Decoding

通常のVAEと同様に潜在変数の平均と分散を取得します. 次に, 再パラメータ化トリックを使用して潜在埋め込みを取得します. その後, decoderに通して再構成トークン行列 $\hat{\boldsymbol{E}}\in\mathbb{R}^{M\times d}$ を取得します. ここで, Appendixにあるアーキテクチャの図を見てみます. Encoderは平均と分散を別々に取得します (実装でもそのようになっています). Transformerは2層で非常に軽量です. 公式実装ではTransformerクラスの中で2層作るようになっています.

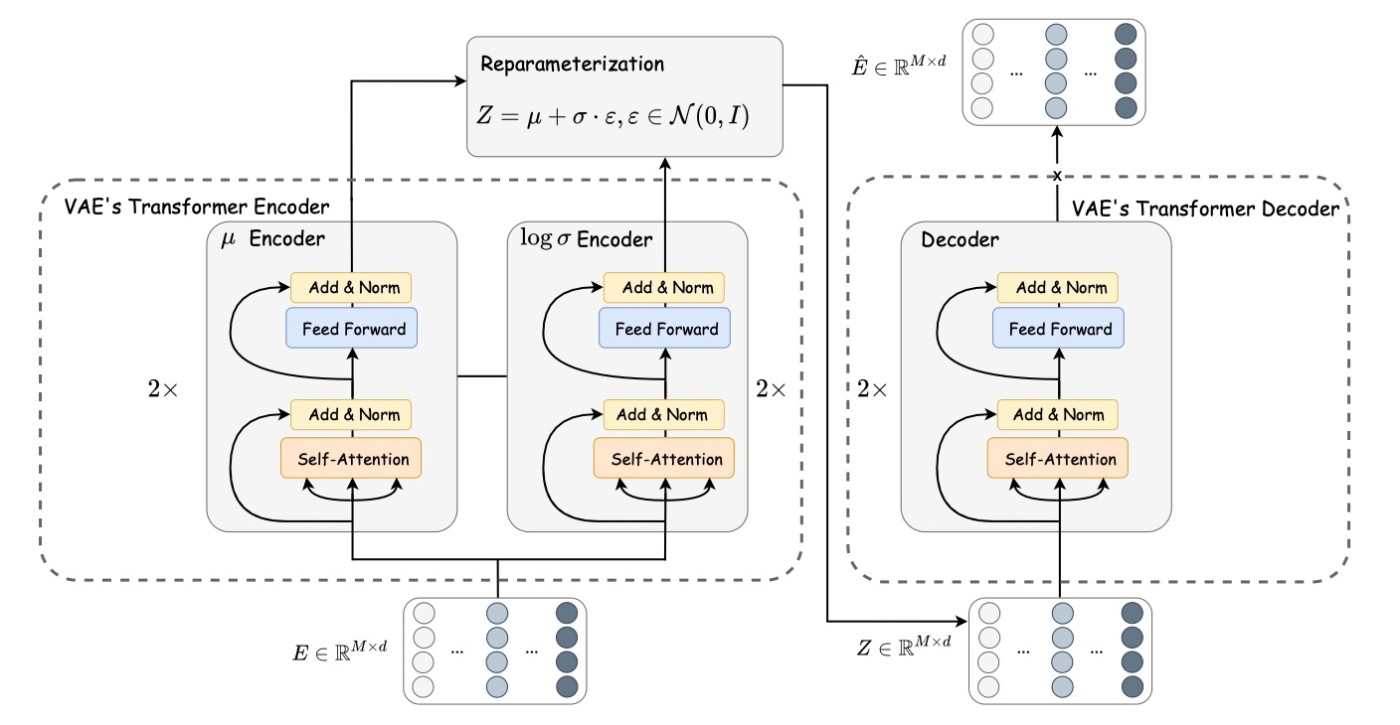
Detokenizer

最後に, token embeddingから実際の値に戻します. tokenizerと対称的な設計にします. すなわち,

\begin{align*} & \hat{x}_i^{\mathrm{num}}=\hat{\boldsymbol{e}}_i^{\mathrm{num}}\cdot\hat{\boldsymbol{w}}_i^{\mathrm{num}}+\hat{b}_i^{\mathrm{num}} \\ & \hat{\boldsymbol{x}}_i^{\mathrm{oh}}=\mathrm{Softmax}(\hat{\boldsymbol{e}}_i^{\mathrm{cat}}\cdot\hat{\boldsymbol{W}}_i^{\mathrm{cat}}+\hat{b}_i^{\mathrm{cat}}) \\ & \hat{\boldsymbol{x}}=[\hat{x}_1^{\mathrm{num}},\ldots,\hat{x}_{M_{\mathrm{num}}}^{\mathrm{num}}, \hat{\boldsymbol{x}}_{1}^{\mathrm{oh}},\ldots,\hat{\boldsymbol{x}}_{M_{\mathrm{cat}}}^{\mathrm{oh}}] \end{align*}

となります. ここでも, $\hat{\boldsymbol{w}}_i^{\mathrm{num}}\in\mathbb{R}^{d\times 1}, \hat{b}_i^{\mathrm{num}}\in\mathbb{R}^{1\times 1}, \hat{\boldsymbol{W}}_i^{\mathrm{cat}}\in\mathbb{R}^{d\times C_i}, \hat{b}_i^{\mathrm{cat}}\in\mathbb{R}^{1\times C_i}$ は学習可能なパラメータです.

Training

定式化が終わったところで, 訓練の詳細です. ここでは効率的な訓練を行うために改良されたVAEの学習方法を用いています. 通常のVAEはELBO損失関数を用いますが, $\beta$ -VAEを使用します. するとlossは以下の式で表されます.

\mathcal{L}=\ell_{\mathrm{recon}}(\boldsymbol{x}, \hat{\boldsymbol{x}})+\beta\ell_{\mathrm{KL}}

$\ell_{\mathrm{recon}}$ は再構成誤差, $\ell_{\mathrm{KL}}$ はKLダイバージェンス損失です.　 $\ell_{\mathrm{KL}}$ を $\beta$ によって重み付けします. 提案手法では $\beta$ が小さいことを期待します. それは, 埋め込み表現がガウス分布に従う必要がないからです. このあと, 拡散モデルで分布を学習するため, 埋め込み表現の分布が既知であることは過剰な条件となります. そのため, 学習中は適応的に $\beta$ をスケジューリングさせて, 再構成の方を重視しつつ適切な埋め込み表現を得ることを目指しています.

スケジューリングの戦略は以下の通りになります.

初期値 $\beta=\beta_{\max}$ でエポックごとの再構成損失 $\ell_{\mathrm{recon}}$ をチェックする.
$\ell_{\mathrm{recon}}$ が一定エポック以上減少しない場合 (これは $\ell_{\mathrm{KL}}$ が支配的であることを表します) は $\beta=\lambda\beta$ でスケールさせます. ここで $\lambda<1$ です. 公式実装では10エポック以上改善が見られない場合は $\lambda=0.7$ によって $\beta$ をスケジューリングしています.
訓練が終了するまで続ける. ただし, $\beta_{\min} <\beta$ が成り立つ間で $\beta$ はスケジューリングされる.

公式実装および論文内の実験では, $\beta_{\min}=10^{-5}, \beta_{\max}=0.01$ でした. ただし, Shoppersデータのみ $\beta_{\max}=0.001$ です. これは論文の主張とやや反します (ハイパーパラメータのチューニングなしに高品質なデータとAppendix G.1で言っていますがこれではデータによって値を変えることになり, 意味がない気がします).

Score-based Generative Modeling

さて, VAEの学習が終わると次はメインとなる拡散モデルの学習が始まります. 先ほどの概要図を再掲します.

真ん中にFlattenと書かれている通り, 埋め込み行列をまずはフラット化してベクトルとして表します.

\boldsymbol{z}=\mathrm{Flatten}(\mathrm{Encoder}(\boldsymbol{x})) \in\mathbb{R}^{1\times Md}

その後, 埋め込みの分布 $p(\boldsymbol{z})$ を学習するために, 以下で表される拡散モデルを考えます. ここで $\boldsymbol{z}_0=\boldsymbol{z}$ はエンコーダーからの初期埋め込みです.

\begin{align*} \boldsymbol{z}_t&=\boldsymbol{z}_0+\sigma(t)\varepsilon,\qquad \epsilon\sim\mathcal{N}(0, \boldsymbol{I})\qquad (\mathrm{Forward Process}) \\ \mathrm{d}\boldsymbol{z}_t&=-2\dot{\sigma}(t)\sigma(t)\nabla_{\boldsymbol{z}_t}\log p(\boldsymbol{z}_t)\mathrm{d}t+\sqrt{2\dot{\sigma}(t)\sigma(t)}\mathrm{d}\boldsymbol{w}_t\qquad (\mathrm{Reverse Process}) \end{align*}

これはスコアベースの式になっています. スコアは $\nabla\log p$ の部分です. 詳しくは以下の2つの論文がベースになっています. $\boldsymbol{w}$ は標準ウィナー過程です.

そのため, 拡散モデルの学習は以下のように行われます.

\mathcal{L}=\mathbb{E}_{\boldsymbol{z}_0\sim p(\boldsymbol{z}_0), t\sim p(t), \boldsymbol{\varepsilon}\sim\mathcal{N}(0, \boldsymbol{I})}\|\boldsymbol{\varepsilon}_{\theta}(\boldsymbol{z}_t, t)-\boldsymbol{\varepsilon}\|^2_2,\ \ \mathrm{where\ } \boldsymbol{z}_t=\boldsymbol{z}_0+\sigma(t)\boldsymbol{\varepsilon}

ここまでの中で登場していた $\sigma(t)$ はノイズの強度を表す関数です. これをどのような関数にするかで微分方程式の解軌道に関わってきます. ここでは $\sigma(t)=t$ を採用します. EDMやDDPMでも同じ関数になるので特別な狙いがあるわけではなく, これまで上手くいっているものを採用したという形です. 論文では, この $\sigma(t)=t$ がreverse processにおいて最小の近似誤差を得られることを補題として示していますが, ここでは省略します. 結論を述べると, これによりsamplingの回数を減らすことができます.

これで拡散モデルのパートは終わりですが, 最後にアーキテクチャを確認します.

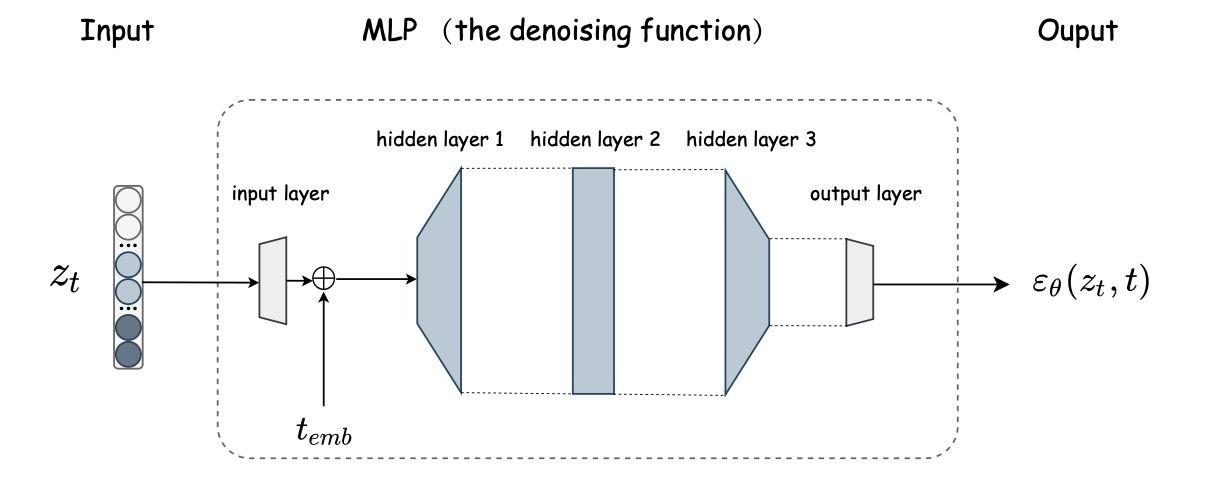
TabDDPM同様非常にシンプルなMLPが使われています. まず最初に入力を射影します. その後, 時間埋め込みを加えてから拡散モデルのパートに移ります. hidden layer1の入力は

\boldsymbol{h}_{\mathrm{in}}=\texttt{FC}_{\mathrm{in}}(\boldsymbol{z}_t)+\boldsymbol{t}_{emb} \in\mathbb{R}^{1\times d_{\mathrm{hidden}}}

です. 全ての実験で $d_{\mathrm{hidden}}=1024$ が使われています. hidden layersはそれぞれの出力次元が $2d_{\mathrm{hidden}}, 2d_{\mathrm{hidden}}, d_{\mathrm{hidden}}$ で, すべて $\texttt{SiLU}$ 関数が活性化関数として採用されています. 最後にoutput layerで埋め込みの次元に戻します.

実験と結果

Adult, Default, Shoppers, Magic, Faults, Beijing, Newsの6つのデータセットを用います.　ベースラインはTVAE, CTGANに加えてグラフベースのGOGGLE, LLMを用いるGReaTと拡散モデル手法であるTabDDPM, CoDi, STaSyの全部で7つです. これまで拡散モデルを用いた手法は統一的な比較がされていなかったのでこの論文は初めて統一的な比較を行うことになります.

評価方法

結果を見る前に評価方法を確認します. この論文では3つの観点で評価します.

低次元統計: column-wise density estimationとpair-wise column correlationを用いてカラム間の相関を確認します.
高次元統計: $\alpha$ -Precisionと $\beta$ -Recallを用いて実データに対する忠実度や多様性を確認します.
下流タスク: machine learning efficiencyとmissing value imputaionで下流タスクの性能を確認します.

結果は全て20回のランダムサンプリングの結果の平均が示されます.

Low-Order Statics

合成データが単一の列の密度を推定し, および列のペア間の相関を評価することから始めます。

まず, 列の密度を調べます. 数値データに対してはコルモゴロフ-スミルノフ検定 (Kolmogorov-Smirnov Test、KST), カテゴリカルデータに対しては全変動距離 (Total Variation Distance、TVD)を用います.

結果を見てみます. 提案手法がどのデータでも最良の結果を示していることがわかります. 拡散モデルのSTaSyとTabDDPMも性能がいいですが, それを上回る形になります.

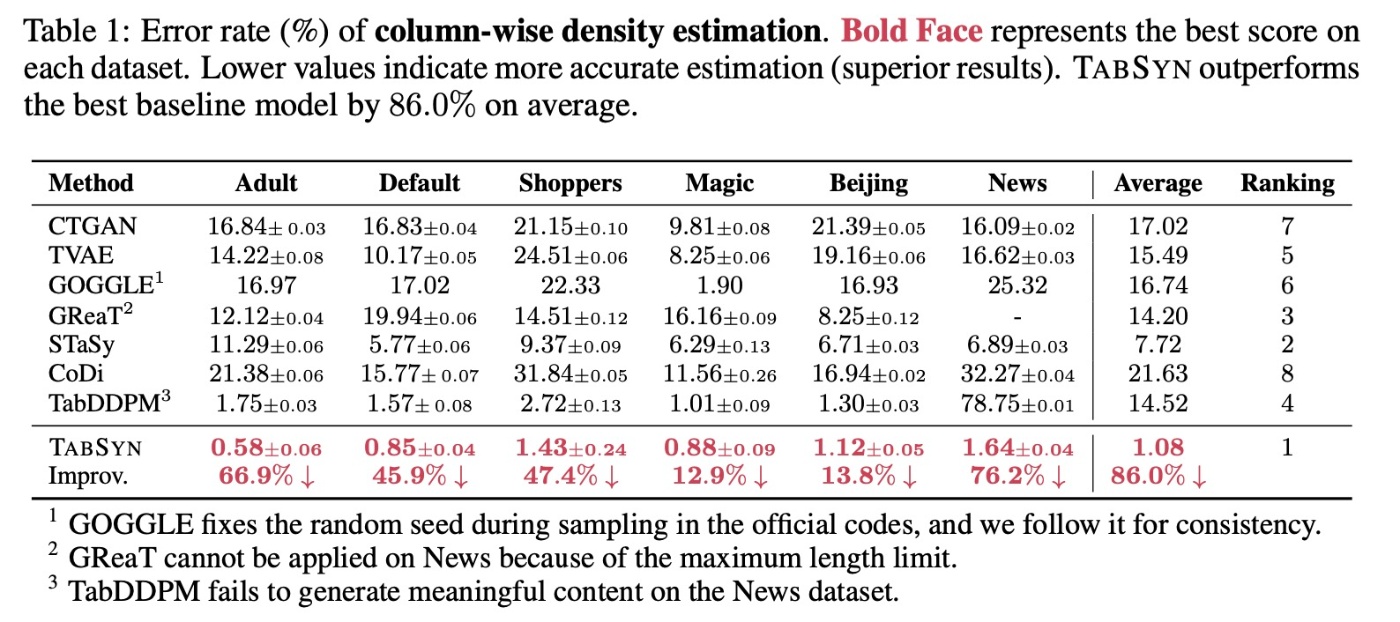
注釈3にもあるように, TabDDPMは意味のある生成ができなかったようです. これについて論文では書かれていませんが, OpenReviewで詳しい話が書かれています. ここでは詳述しませんが, 簡単に述べるとモード崩壊が発生しているようです.

続いてカラムごとの相関を見てみます. 数値データ同士ではピアソン相関, カテゴリデータ同士はcontingency similarityを用います. 数値データとカテゴリデータの相関は, まず数値データをバケット分割してカテゴリ値にグループ化し, contingency similarityを計算します.

では, 結果を確認します. これを見ると先ほどと同様の結果になります. ただし, 先ほどは3番目のrankを誇っていたGReaTが8位に落ちていることがわかります. これは自己回帰言語モデルがカラム間の相関を捉えることができていないことを示しています.

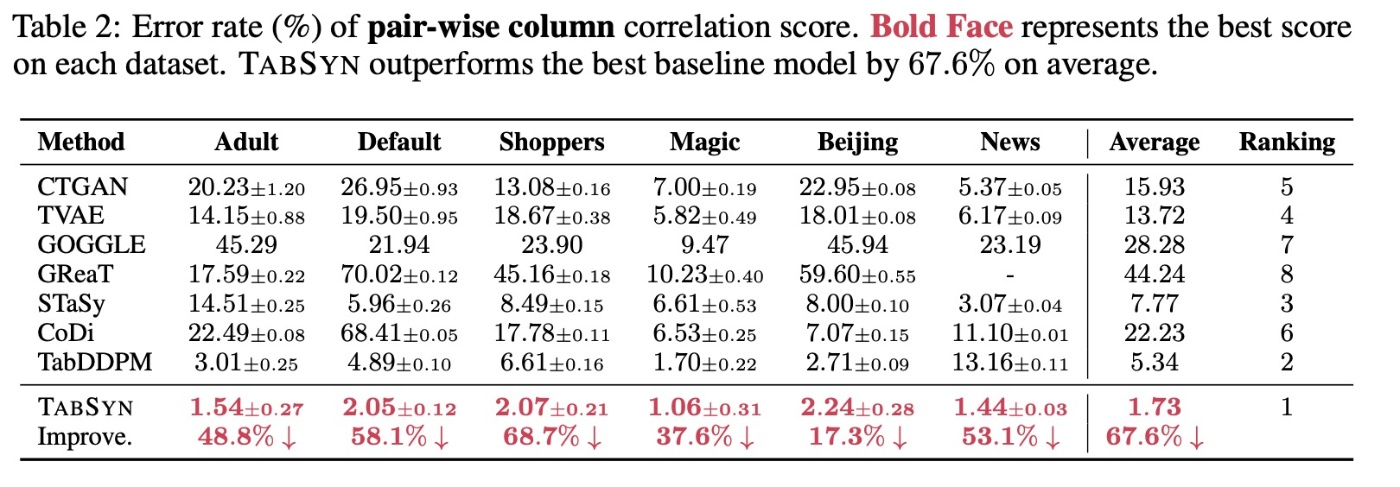
High-Order Statics

main paperの部分で触れられていないので著者らがメインで主張したいことではなさそうですが, こちらもみていきます. $\alpha$ -Precisionと $\beta$ -Recallという聞き慣れない指標を使っていますので, 評価指標の説明を軽くします.

$\alpha$ -Precisionはどれだけ生成データが実データの分布由来であるかを示しています. $\beta$ -Recallは生成データの多様性を示しています. 言い換えると, 生成データと実データがどれだけ近いかを表しています. 当然ですが, $\beta$ -Recallが大きいとデータがコピーされた疑いがあります. $\alpha$ -Precisionと $\beta$ -Recallを提案した論文では第三の指標としてAuthenticityも提案されていますが, $\beta$ -Recallとは負の相関があるため使われていません.

詳しくは提案論文をご覧ください.

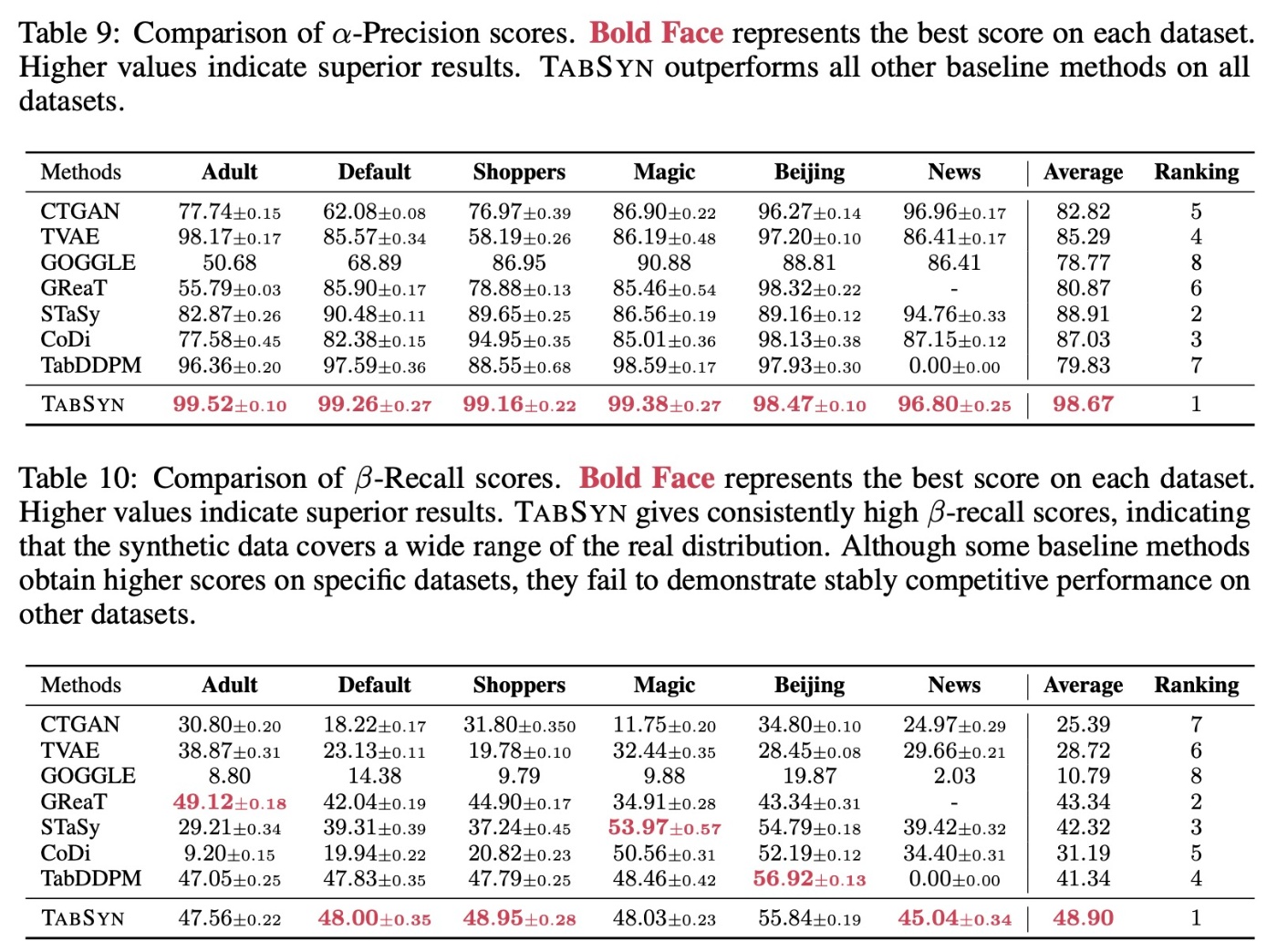
結果を見ていきます. 2つの指標は併用するもので, 特に $\alpha$ -Precisionを見てから $\beta$ -Recallを見ます. $\alpha$ -Precisionを見ると, 提案手法は非常に本物に近いデータを生成しています. $\alpha$ -Precisionが低いと実データの多様体から離れてしまいます. 次に $\beta$ -Recallをみます. $\beta$ -Recallでも非常に高い性能を誇っています. なお, この後見る下流タスクの結果とは相関がありません.

個人的な意見ですが, この指標での性能比較と下流タスクの性能比較は一致していないのでAppendixになったのではないかと思います.

下流タスクでの結果

実世界のデータは金融データや医療データなどが代表例に挙げられるように, 非常にセンシティブです. そのため, 本物の表データを使うのではなく生成データを使うモチベーションが非常に大きいです. ~~論文ではプライバシーの話をここでしていますが, なおさら $\beta$ -Recallで評価した意味がわからなくなっています.~~ (arXiv版ではあったこの内容の話がICLRのcamera-readyでは消えていました. 査読者のコメントでも同様の指摘がありました. 査読を見てみるとDCRを用いてプライバシーの比較をしており, 他の拡散モデルの手法と同程度であることがわかります.)

まず, Machine Learning Efficiencyの結果を見ます. この論文ではXGBoostを用いています. こちらの結果でも非常に高性能な結果が示されています. 一方でこれまでの統計的比較と比べると手法間の差は縮まっています. これは表データは余分な情報が多いために, そこはGBDTの評価に大きな影響を与えないためと考察されています.

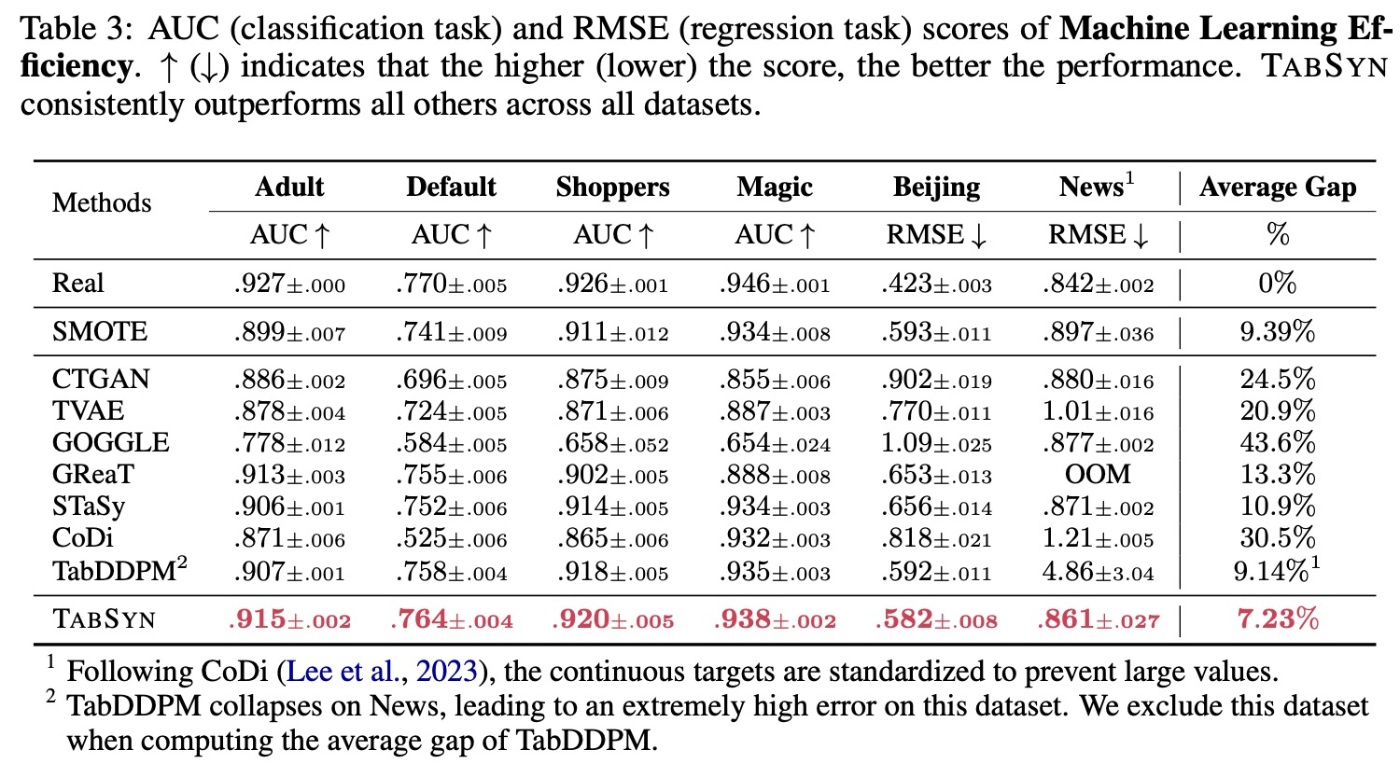
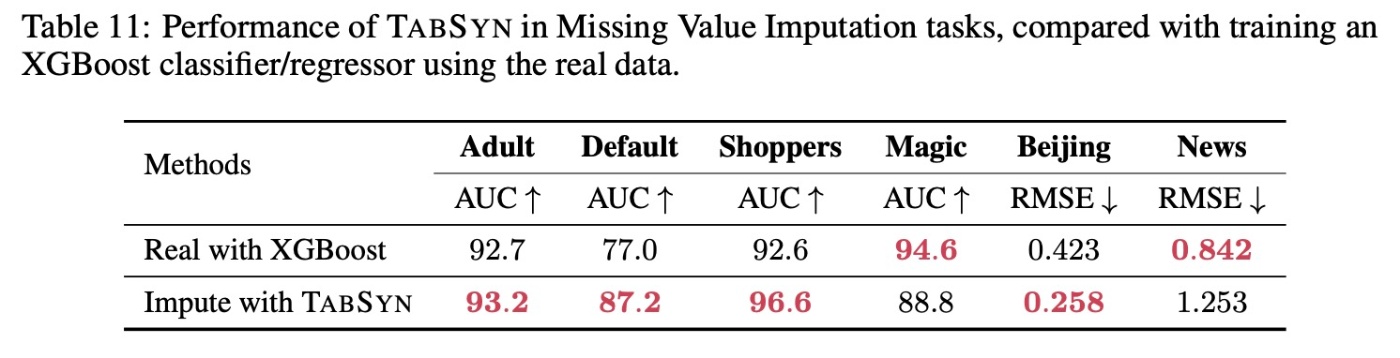
続いて, 欠損値補完についてみます. 拡散モデルの特徴として, 追加訓練なしで欠損値補完ができることが挙げられます (画像データではimage inpaintingが相当します). 簡単に手法を紹介すると, RePaintと同様の手法になります. すなわち, マスクされていない部分は元のデータの値を用いて, maskされた部分にのみモデルの予測結果を適用するという手法です. 目的変数をmaskして, 通常のclassificationやregressionと同等の状況に設定します.

RePaintについては以下の論文を参照ください.

ここではXGBoostとの比較を行います. unconditional generationな拡散モデルが使えるという話だったのにXGBoostとのみ比較というのは気になりますが, Appendixに結果が載っている以上, あまり主張のメインではないのではと思います. 結果を簡単にみます. 多くのデータでXGBoostと比較して競争力のある結果とわかります.

Ablation Study

最後にablation studyを見ます. ここでみるのは以下の3つです.

スケジューリング $\beta$ -VAEの効果
線形ノイズ強度の効果
encoding/decodingの手法の比較

スケジューリング $\beta$ -VAEの効果

$\beta$ -VAEの $\beta$ の値を学習状況に応じてスケールさせていました. $\beta$ をさまざまな値で固定したときと, スケジュールさせたとき (提案手法)との比較を見ます. 4000エポックに渡って損失を見ます.

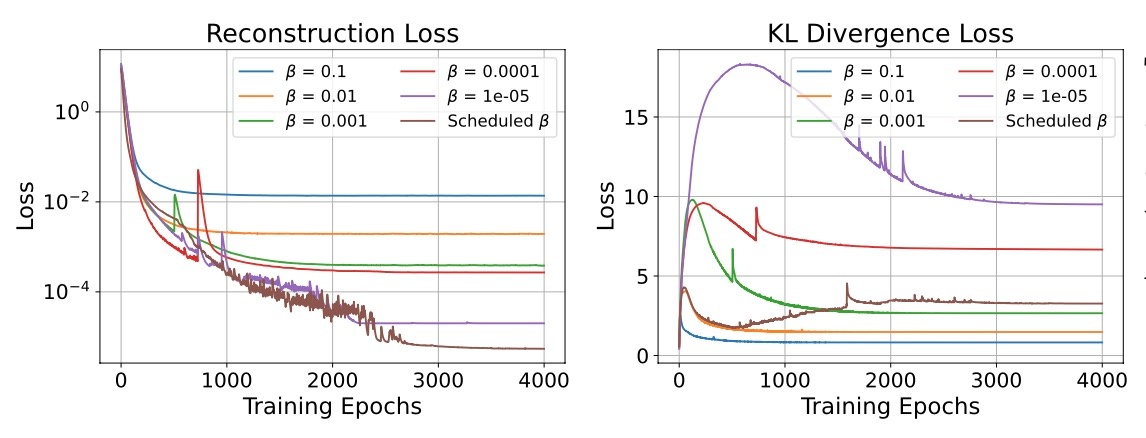
再構成誤差は $\beta$ をスケジュールさせることによって最も低い値になることがわかります. 右側のKLダイバージェンスlossと併せて見てみると, $\beta$ が固定の時は $\beta$ の大きさによって再構成誤差とのトレードオフの関係があるように見えます. 一方でスケジュールさせた場合はトレードオフのちょうどいい具合に収まっていることがわかります.

論文には書かれていませんが, $\beta$ -VAEは $\beta$ の値によるトレードオフがあることが知られています. 以下の論文などがわかりやすいかなと思います.
https://arxiv.org/abs/1804.03599

線形ノイズ強度の効果

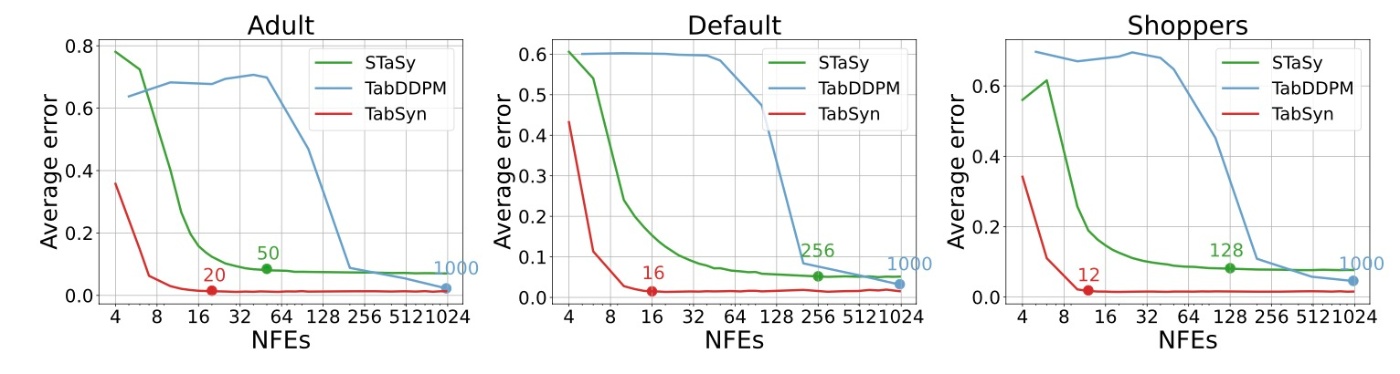
$\sigma(t)=t$ の線形ノイズ強度を採用していましたがこれを用いることで少ないsampling stepsで高品質な生成が可能であることを確認します.

TabDDPMやSTaSyと比較すると少ないステップ数で高品質な生成を行えていることがわかります.

encoding/decodingの手法の比較

提案手法ではVAEでデータを射影していました. これを別の方式にするとどうなるかを調べています. 以下の2つの手法での実験を行っています.

TabSyn-OneHot: VAEをone-hotに置き換える. すなわちカテゴリデータをone-hotで表して, それらも数値データとして扱う手法
TabSyn-DDPM: SDE-basedでモデリングされていたものをDDPMに置き換える

Adultデータを用いた結果を見てみます. ここではlow-order staticsのみを見ます.

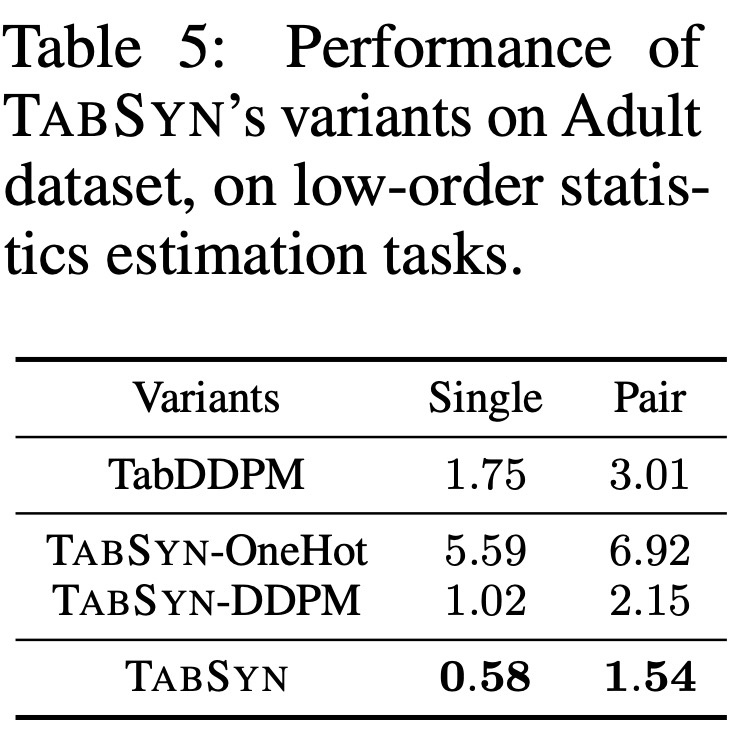
まず, one-hot vectorをそのまま数値データとして扱うと, 大幅に精度が低下します. この考察はされていませんでした. また, 潜在空間でのDDPMはデータ空間でのDDPMを上回る結果を得ており, データ空間より潜在空間でのモデリングが適していることがわかります. これは画像生成とは異なる結果なので興味深いです. さらに, 提案手法はそれらを上回る結果です.

Speed

最後に, 訓練時間と生成時間の比較をしておきます. 論文のIntroductionではspeedを利点として挙げながらもmain paperでは言及がありませんが, Appendixに少しあります. 詳しい比較の設定は書かれていませんが, Adultデータで確認します.

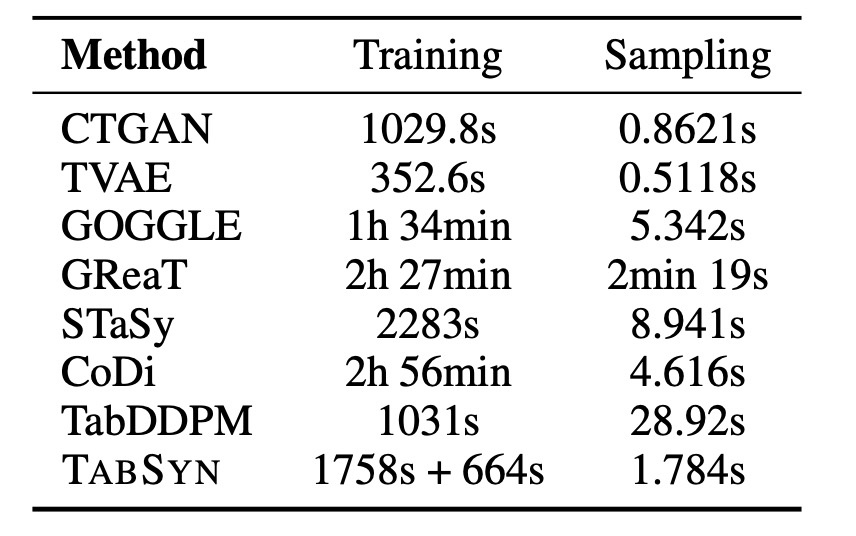
提案手法は2つのモデルを訓練する必要があります. そのため, それなりに時間がかかりますが, 40分程度でできることがわかります. 一方で, 生成速度は非常に高速で, 1ステップ生成のGANやVAEに迫る勢いです. なお, 公式実装を確認すると拡散モデルの部分はearly stoppingが実装されていますが, 論文ではそれについての言及がありませんでした. デフォルトのエポック数をちゃんと訓練させようとするともう少し時間がかかりそうです.

まとめ

データを潜在空間に射影してそこで拡散モデルを学習するTabSynの提案
既存手法と比較して性能向上を確認
欠損値補完にも適用可能で, XGBoostと同等の性能を達成

思ったこと

OpenReviewをみると査読のコメントに対して非常に的確な返答がされているなと思いました. 追加の実験量も多く, これが口頭発表になるのも納得です.
LDMを使うことは誰でも考えつきそうですが, 表データの特性を踏まえた設計などの工夫がすごいと思いました.
Metareviewでも書かれていますが, コードも整理されていて, 見習うべき点が多いと思いました.
shoppersだけ $\beta_{\max}$ が異なる理由は書かれておらず, そこが気になりました.
また, TabDDPMやCoDi, STaSyと比較して, 使用しているデータの種類が少なく, 効果が限定的に見えてしまいます.
GANベースの手法は表データでも優位性が失われつつあるように思える結果です.
TabDDPMの論文が恐らくきっかけとなって, SMOTEをベースラインに採用する事例が増えているように思います. この論文でもICLRのcamera-readyではSMOTEが追加されています.
まだ表データドメインでは基盤モデルが登場していませんが, そろそろ登場しそうな気配があります (特に, TabSynが分類器と同等のパフォーマンスを出した点は特筆すべきで, これを任意のデータに拡張することで構築できそうです). ただ, 表はデータごとに特性がかなり異なるのでかなり難しそうです.
査読に対する反論ではMLPの代わりにResidual ConnectionやTransformerを用いた結果が示されていますが, MLPの方が性能がいいことがわかっています. シンプルなのに複雑なアーキテクチャより高性能であることは驚きです. 一方でVAEのパートはTransformerを用いているのでかなりのエポック数を要します (公式実装は4000エポック). この改善が今後の課題になりそうです.
VAEでは $M\times d$ 次元に埋め込みをしていますが, これはカラムが増えると埋め込みの次元が大きくなることを表します. 論文では $M$ が大きくても50程度ですが, さらに増える場合などは考えられるのか気になります.

参考文献

Hengrui Zhang and Jiani Zhang and Zhengyuan Shen and Balasubramaniam Srinivasan and Xiao Qin and Christos Faloutsos and Huzefa Rangwala and George Karypis. Mixed-Type Tabular Data Synthesis with Score-based Diffusion in Latent Space. The Twelfth International Conference on Learning Representations, 2024 (https://openreview.net/forum?id=4Ay23yeuz0)
Ahmed Alaa, Boris Van Breugel, Evgeny S Saveliev, and Mihaela van der Schaar. How faithful is your synthetic data? sample-level metrics for evaluating and auditing generative models. In International Conference on Machine Learning, pp. 290–306. PMLR,2022. (https://proceedings.mlr.press/v162/alaa22a.html)
Andreas Lugmayr, Martin Danelljan, Andres Romero, Fisher Yu, Radu Timofte, and Luc Van Gool. Repaint: Inpainting using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 11461–11471, 2022. (https://openaccess.thecvf.com/content/CVPR2022/html/Lugmayr_RePaint_Inpainting_Using_Denoising_Diffusion_Probabilistic_Models_CVPR_2022_paper.html)

拡散モデルと表データ生成④：【論文】TabSyn

Mixed-Type Tabular Data Synthesis with Score-based Diffusion in Latent Space (ICLR2024)

関連情報

書籍情報

TL;DR

提案手法: TabSyn