🙆

時系列基盤モデルへ③：TimesFM【論文】

2024/06/27に公開

機械学習

論文

時系列

tech

A decoder-only foundation model for time-series forecasting (ICML2024)

はじめに

Googleから発表されたTimeFMの論文です. foundation modelといいつつfor time-series forecastingじゃないかと思いますが, その通りです.

個人的にはこれを時系列基盤モデルのひとつとしてカウントしていいのか怪しい部分があると思いますが, とりあえず内容をまとめることにします.

提案モデルであるTimesFMは主に2つの特徴があります.

real world dataと量と多様性を確保した合成データで訓練されていること
パッチ化を入力とするdecoder style attention architectureを採用し, 効率的に時系列データの事前学習を行なっていること

問題設定

時系列予測のためのモデルなので, 問題設定も時系列予測タスクです. $L$ 個の連続した時系列が与えられたとき, 続きの $H$ 個を予測することが目標です. 数式で書くと

f: (\boldsymbol{y}_{1:L})\longrightarrow\hat{\boldsymbol{y}}_{L+1:L+H}

です. ここで, $\boldsymbol{y}_{1:L}=\{y_1,\ldots,y_L\}$ は入力系列です. 添え字はnumpy likeに書かれており, 以降でもその書き方を採用します.

アーキテクチャ

予測に限らず, 時系列基盤モデルは変量や系列長の異なる様々なデータに対応する必要があります. また, 事前学習の段階でモデルは様々なデータを扱える容量が必要です. NLPではTransformerが異なるcontext lengthに対応できることがわかっていますので, ここでもTransformerを用います. しかし, 時系列特有の設計選択があり, 以下の4つとなります.

Patching
PatchTSTと同様に, 時系列をパッチ分割します. このパッチはNLPでいうトークンに似たもので, これにより性能向上が見込めます.
Decoder-only model
PatchTSTとの違いはdecoder onlyのモデルで訓練されることです. すなわちモデルはパッチの列が与えられたときに次のパッチを予測します.
Longer output patches
LLMではほとんどが一回で予測するのはひとつのトークンです (たまに複数のトークンを予測したりする研究もあります). 先行研究では, 対象系列を全て一度に予測した方が性能がいいことが観察されています. しかし, zero-shotで予測する場合などは系列長が事前にはわからないので不適当です. ここでは, 出力パッチを入力パッチより長くすることで中間的なアプローチを採用します.

例を考えてみます. 入力パッチの長さが32で出力パッチの長さが128とします. 訓練時, モデルは最初の32パッチから次の128ポイントを予測し, 最初の64パッチから次の128パッチを予測し... といったような学習を行います.

推論時は, 長さ256の時系列が与えられ, 256系列を予測するとします. モデルはまず257からの128ポイントを予測します. その後, 与えられた256系列と予測した128系列を条件としてさらに128系列を予測します.

出力パッチの長さが入力パッチの長さの32に固定されている場合は8回予測を行う必要がありますが, 128であれば2回で済みます. しかし, 出力パッチの長さが長すぎると出力パッチより短い時系列 (ex. 月次など)を扱うことが難しくなるというトレードオフが発生します.
Patch Masking
ランダムマスキングを行うことでパッチ長の整数倍の系列長のみしか予測できなくなるという状況を解消します.

指針を確認したので, モデルの概要図を示します.

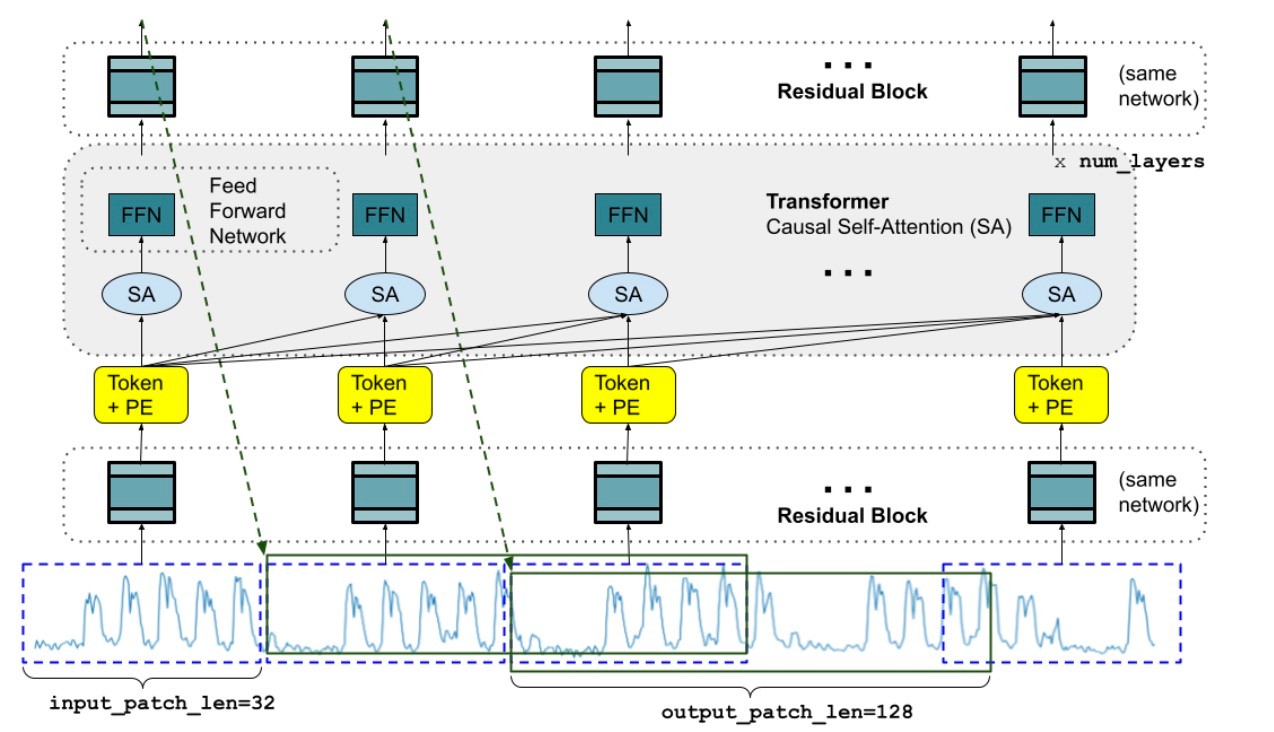
順々にみていきます.

Input Layer

入力層の役割は時系列データをTransformerに入力するトークンに前処理を行うことです (Patching). まず, 入力を重複がないようにパッチに分割します. 次に, 各パッチをResidual Blockによって model_dimのベクトルにします. 入力とともに, マスク $\boldsymbol{m}_{1:L}$ も与えます. Residual Blockは隠れ層1のMLPで, 詳細は示されていませんがTiDEで用いられているものと似ていると述べられています. TiDEの論文から引用すると以下の構造です.

Long-term Forecasting with TiDE: Time-series Dense Encoderより引用

パッチサイズを $p$ とすると, $j$ 番目のパッチは $\tilde{\boldsymbol{y}}_j=\boldsymbol{y}_{p(j-1):pj}$ と表されます. 同様にマスクも $\tilde{\boldsymbol{m}}_j=\boldsymbol{m}_{p(j-1):pj}$ とパッチ化できます. 入力層に通すとTransformerへの入力トークンは

\boldsymbol{t}_j=\mathrm{\texttt{InputResidualBlock}}(\tilde{\boldsymbol{y}}_j\odot(1-\tilde{m}_j))+\mathrm{\texttt{PE}}_j

と書けます. ここで, $\mathrm{\texttt{PE}}_j$ はオリジナルのTransformerで定義された位置エンコーディングです. 入力トークンは $N=\lfloor L/p\rfloor$ 存在します.

Stacked Transformer

特に述べることもない, 通常のTransformerのdecoderを並べたものです. FFNの隠れサイズは, model_dimと同じに設定します. 通常のLLM同様, 未来のトークンを見ないようにするcausal self-attentionを用いています. 数式で書けば $j\in[1, N]$ として

\boldsymbol{o}_j=\mathrm{\texttt{StackedTransformer}}((\boldsymbol{t}_1, \dot{m}_1), \ldots, (\boldsymbol{t}_j, \dot{m}_j))

です. $\dot{m}_j$ は $j$ 番目のトークンが完全にマスクされていないかを表します. $\dot{m}_j=0$ のとき, マスクされたデータポイントは存在しないです.

Output Layer

最後に, 出力トークンを時系列データにマッピングします. 入力パッチの長さとは異なる長さのパッチを出力する必要があるので, 以下のような設計になります.

\hat{\boldsymbol{y}}_{pj+1:pj+h} = \mathrm{\texttt{OutputResidualBlock}}(\boldsymbol{o}_j).

ここで, 出力パッチの長さは $h$ です. 入力時とは別のResidual Blockを用います.

Loss Function

損失関数はMSEを用います. これは, 予測に関心があるからで, 例えば予測確率が知りたければ出力パッチに対して複数のヘッドを持たせるなどが考えられます.

Training

いったって標準的な学習方法のため, この論文特有の戦略についてのみ触れます. まず, マスクについてですが, 一様分布で $r\in[0, p-1]$ をサンプリングします. そして, $\boldsymbol{m}_{1:r}=1$ とし, 残りは0とします. これは, 1から最大系列長までを全てカバーできる戦略になります.

Inference

推論時, 与えられる系列長が $p$ の倍数であれば非常に簡単です. そうでない場合は $p$ の倍数になるまで0埋めを行います. その後, 対応する部分をマスクします.

事前学習

冒頭でも触れたように, 実データと合成データを組み合わせて用います.

Google Trends
数百万のクエリに対する時間経過に伴う検索関心をとらえたデータです. 今回は2007年から2022年までの15年間のデータを元に22000のクエリを用意します. これ以上クエリを増やすとデータがスパースになってしまうようです. 各クエリに対して時間ごと, 日次, 週次, 月次の粒度でデータをそれぞれダウンロードし, データセットを作ります. 時間帯は時間ごとのデータが2018年1月から2019年12月, その他の粒度が2007年1月から2021年12月までです. おおよそ5億データポイントとなります.
Wiki Pageviews
wikipediaのすべてのページの時間ごとのビューを記録したデータです. 2012年1月から2023年11月までのすべてのビューデータをダウンロードし, ページごとにビューを時間ごと, 日次, 週次, 月次の粒度で集計し, スパースなビューをフィルタリングしています. おおよそ3兆データポイントです.
Synthetic Data
ARMAプロセス, 季節パターン (異なる周波数の正弦波と余弦波の混合), トレンド (線形、指数的でいくつかの変化点を持つ), step functionの生成器を作成し, データを作ります. 合成時系列はこれらのプロセスを1つ以上組み合わせることで作成し, 全部で2048系列のデータが300万あります.
Other real-world data sources
M4などの実データも用います. ただし, 実データの大半はGoogle TrendとWiki Pageviewsです.

事前学習で用いたデータは以下のようにまとめられます.

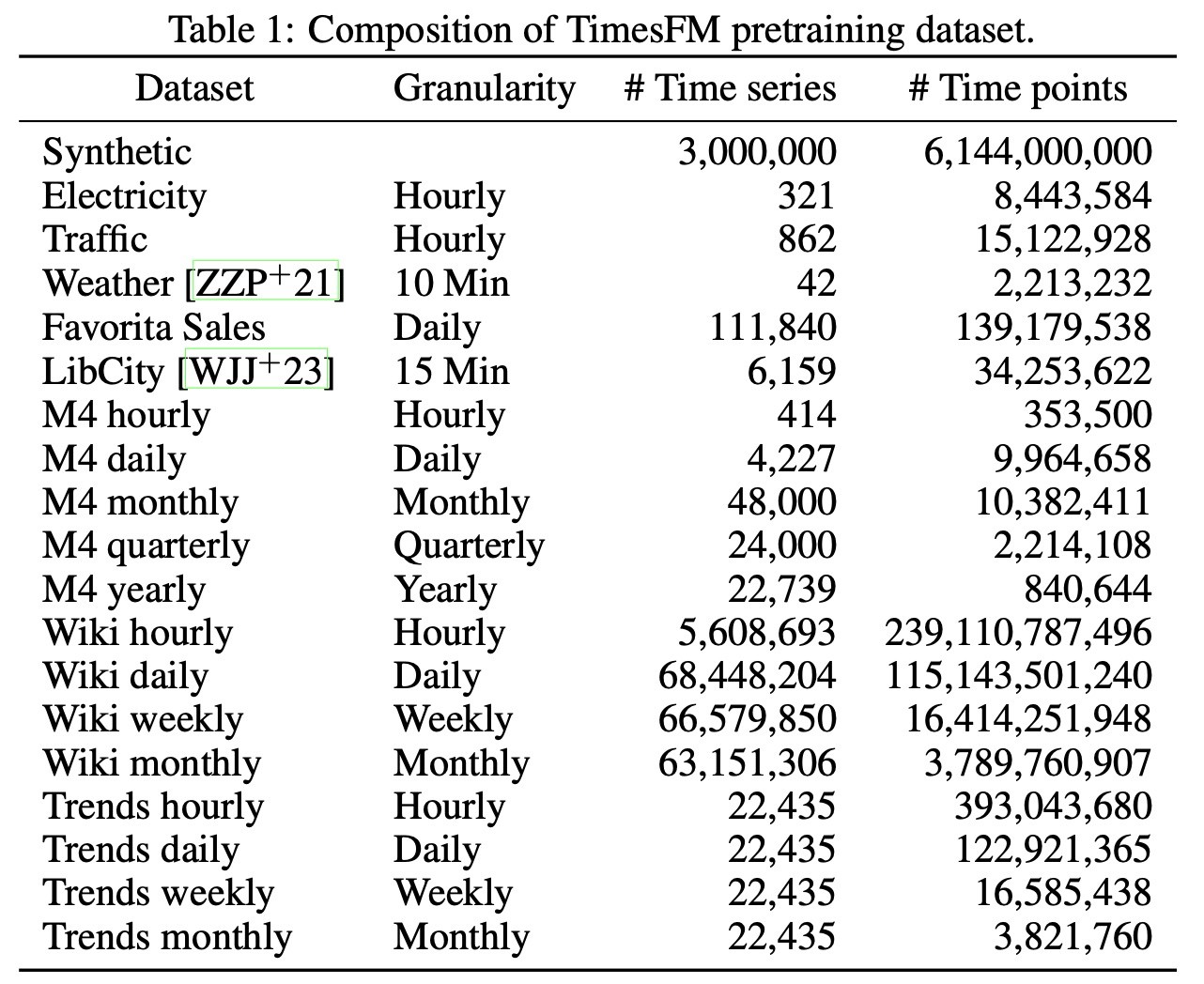
実際には実データと合成データを混合して訓練します. training loaderは80%の実データと20%の合成データをサンプリングします. 実データはその粒度に対して均等な重みを与えています. 週次, 月次以外の場合は系列長に余裕があるのでcontext lengthは512を用いますが, 週次は256を用います. 月次の場合は64を用います. 標準正規化を用います. すなわち時系列は最初の入力パッチの平均と標準偏差でスケーリングされます.

詳しい学習詳細は示されていません.

結果

基本的にzero-shotでの評価を行います. 評価データはMonash, Darts, ETTです.

Monashは欠損値を含むデータを除外した結果, 18のデータセットが残りました. 評価指標は全データセットの平均MAEです.

Dartsはすべてのデータを用います. ここで, Dartsのデータは多くの時系列を扱うブログ等で用いられているため, LLMTimeの結果はリークしている可能性が高いことに注意が必要です. このデータでもMAEを用います.

EETはInformerデータセットのものを用います. なぜ全部使わないのかというと, 単純に事前学習で一部を使ってしまっているからです. これは長期予測のためのデータなのですが, LLMTimeで扱うには数百万トークンに相当するのでお金がかかりすぎます. そのため, 最後のtest windowのみで比較します. これもMAEを用います.

結果を示します.

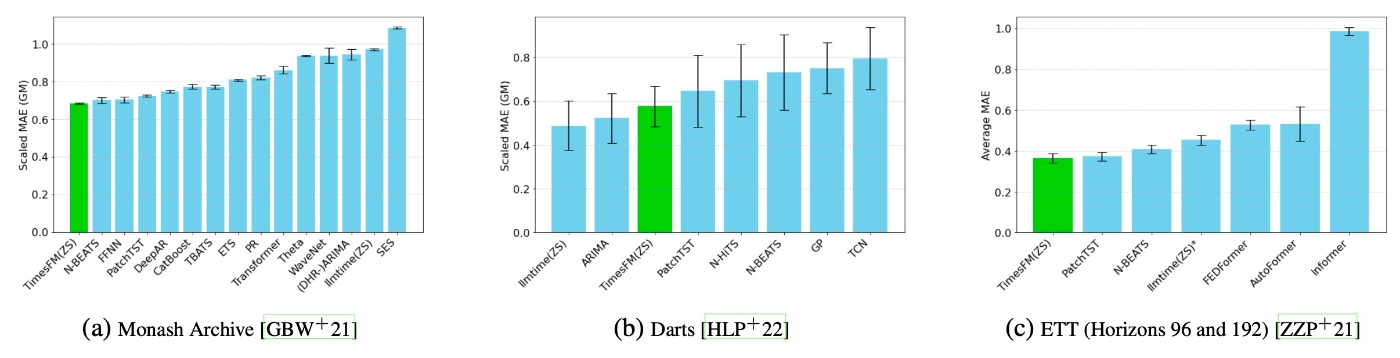
全体として, 非常に高性能で様々なデータに対応していることがわかります. PatchTSTより優位な結果が示されており, また, 他の深層学習モデルと比較してもその性能の良さは明らかです. DartsではARIMAに負けていますが, ARIMAが季節性などのエンコーディングを手動で行う必要があることを踏まえると手軽さという点で優位に立てるというのが著者らの主張です.

Ablation

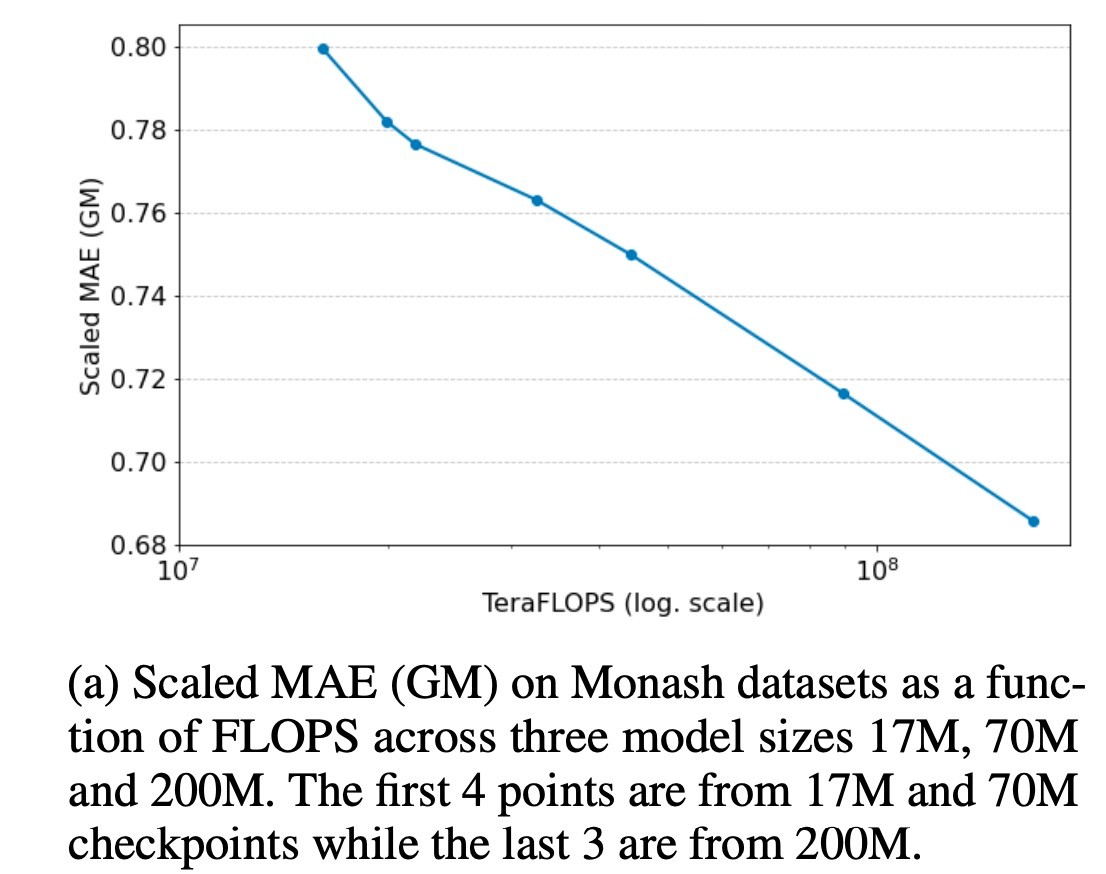
Scaling

LLMの文脈では大雑把にデータとモデルサイズを適切に増やすと性能が向上するというスケーリング則があります. そこで, 訓練データは固定してモデルサイズを変化させます. Monashでのscaled MAE (GM)とFLOPSの関係性をグラフにしたのが下図です. 左から4つのプロットが17M, 70Mのモデルのもので, 右3つが200Mのものですが, モデルサイズが大きくなると性能が良くなることがわかります. 実験は16個のテンソルコアを持つTPUv5eで行われていますが, 200Mのモデルが1.5M iterations学習するには2日かかります. LLMなどと比較してパラメータが小さいこともありますが, それなりにお手軽です (一般環境で再現可能とは言っていません).

Autoregressive Decoding

最初の方でも触れましたが, 最近の長期時系列予測ではdecoderから一度にすべての系列を予測する方が性能がいいことが示されています. 基盤モデルでは予測する系列の長さが未知であるため, その通りにはならないかもしれません. しかし, 入力パッチの長さよりも出力パッチの長さを長くすることで自己回帰の回数を減らしています.

実際に, ETTのテストデータを用いて512系列を予測するタスクを行います. 出力パッチが長くなるほど性能の向上が見られます. 個人的には何回も自己回帰をすることを前提に設計されているので途中で性能向上が終わり, 性能が悪化する推移をすると思うのですが, これより長い系列長での結果はありません.

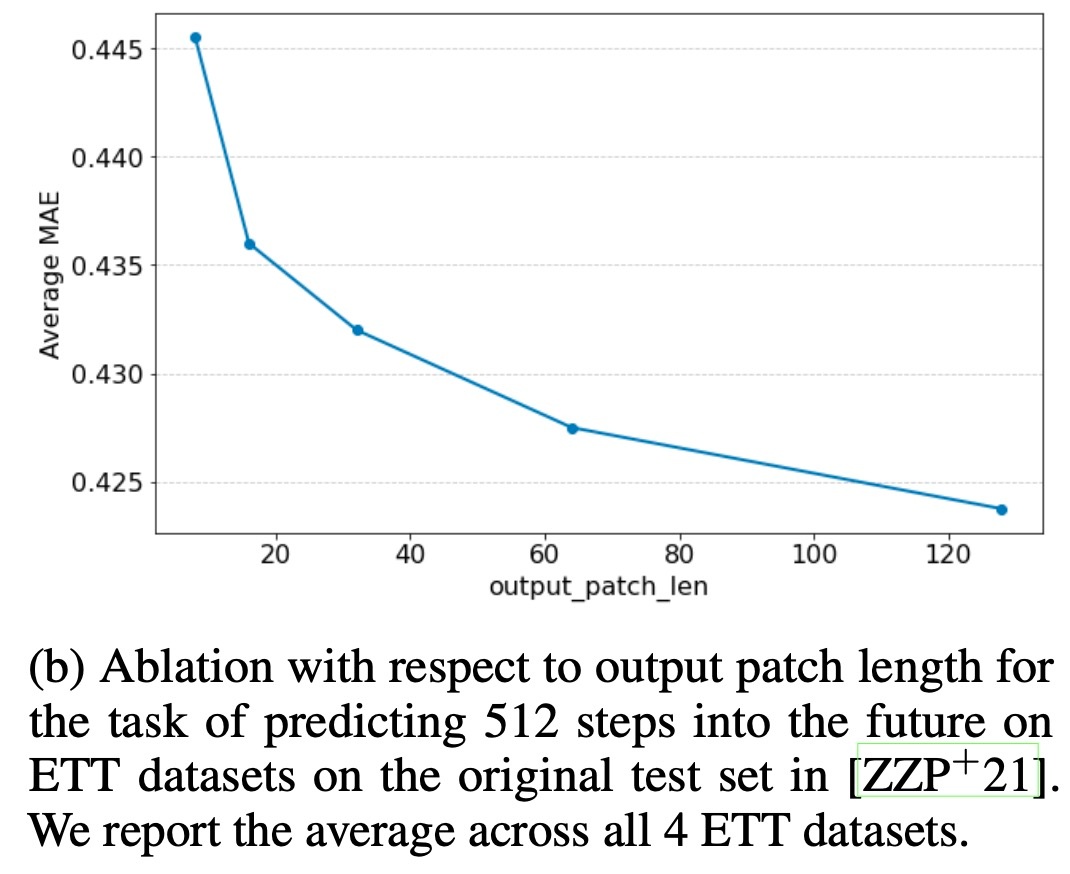
Input Patch Length

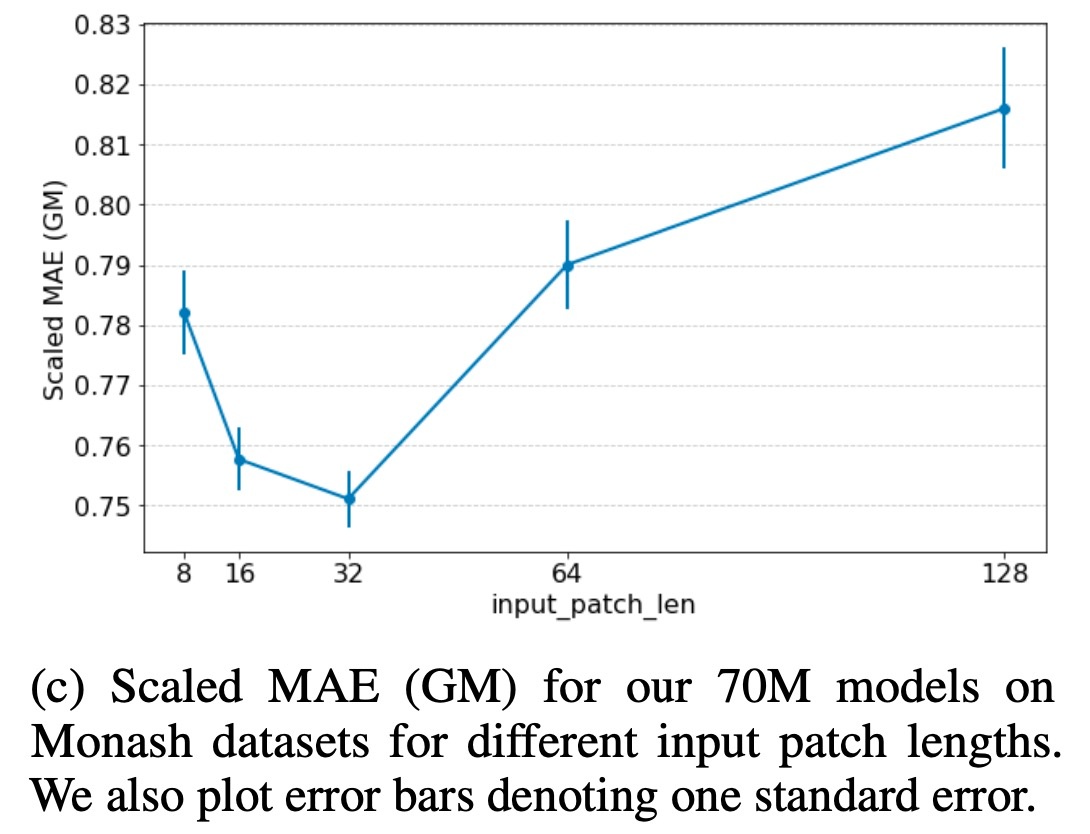
入力パッチ長を大きく取ると, decoderではなくencoder styleの学習戦略になるので性能低下が予想できます. 実際に入力パッチ長を変化させると, $p=32$ までは性能向上が見られますが, その後は性能が低下します. ちなみに $p=32$ を基準とすると訓練時間は $p=16$ が2倍, $p=8$ が3倍なので高速に最高性能を達成できます.

Dataset Ablation

合成データの検討です. 直感的な話として, 実世界のデータは多くが一般的なサンプリングの粒度を持っていて, 特定の周期性もあります. そのため, 実データだけでは特定の周波数にのみ対応してしまい, 汎化性能を持たないことが考えられます. 実際に, 合成データの有無での比較を行ったのが下のグラフです.

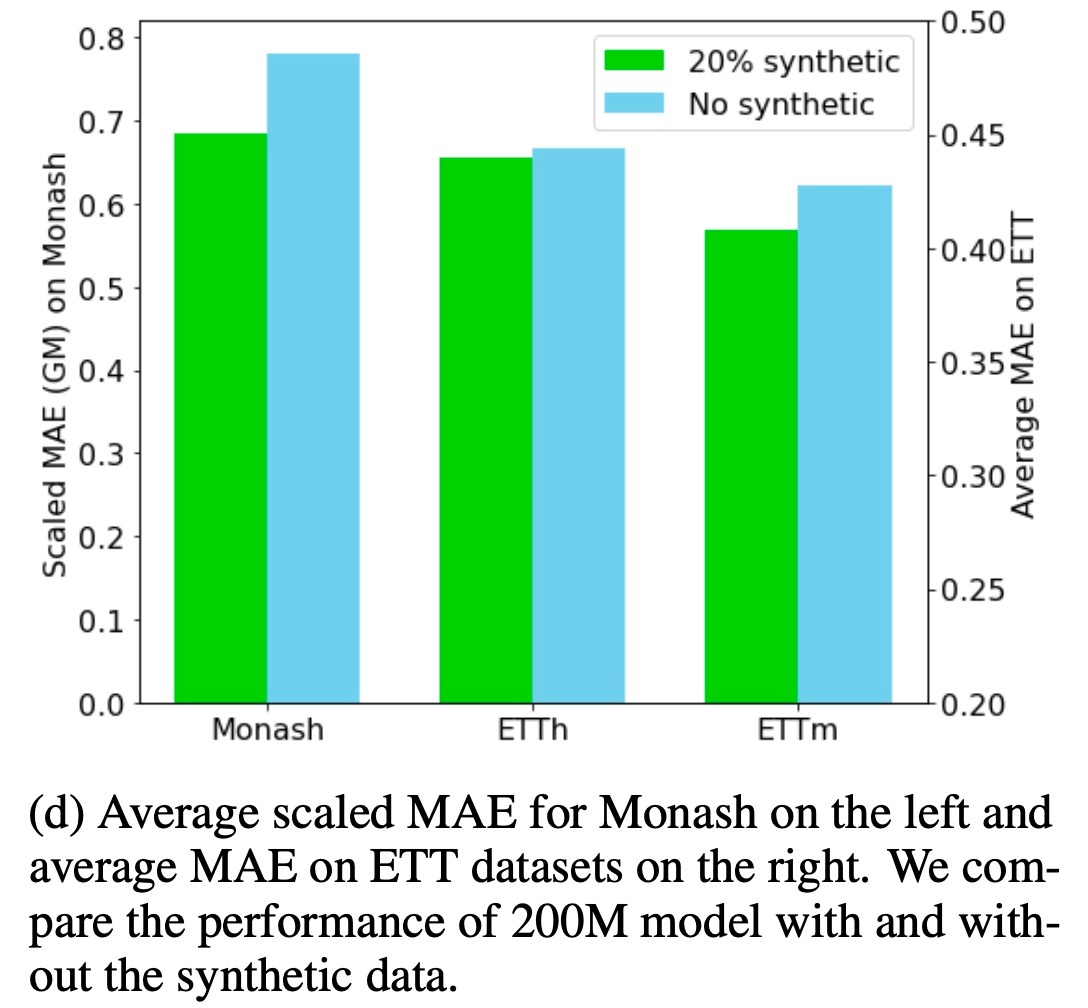
Monashは四半期, 年間, 10分などの十分に表現されていない粒度を持っているために性能の低下が確認できます. しかし, ETTは粒度が適当であるためにあまり大きな性能低下は見られません. ただし, 15分の粒度のETTmでは性能低下が見られます.

可視化

最後に, 論文のAppendixに載っている予測結果を可視化したものの一例を見ます. 比較手法はLLMTimeとARIMAです. これを見ると, 色々なデータで紫のLLMTimeや赤のARIMAが目立つことが確認できますが, 青のTimesFMはそこまでではないです. たしかに, 性能はよさそうです.

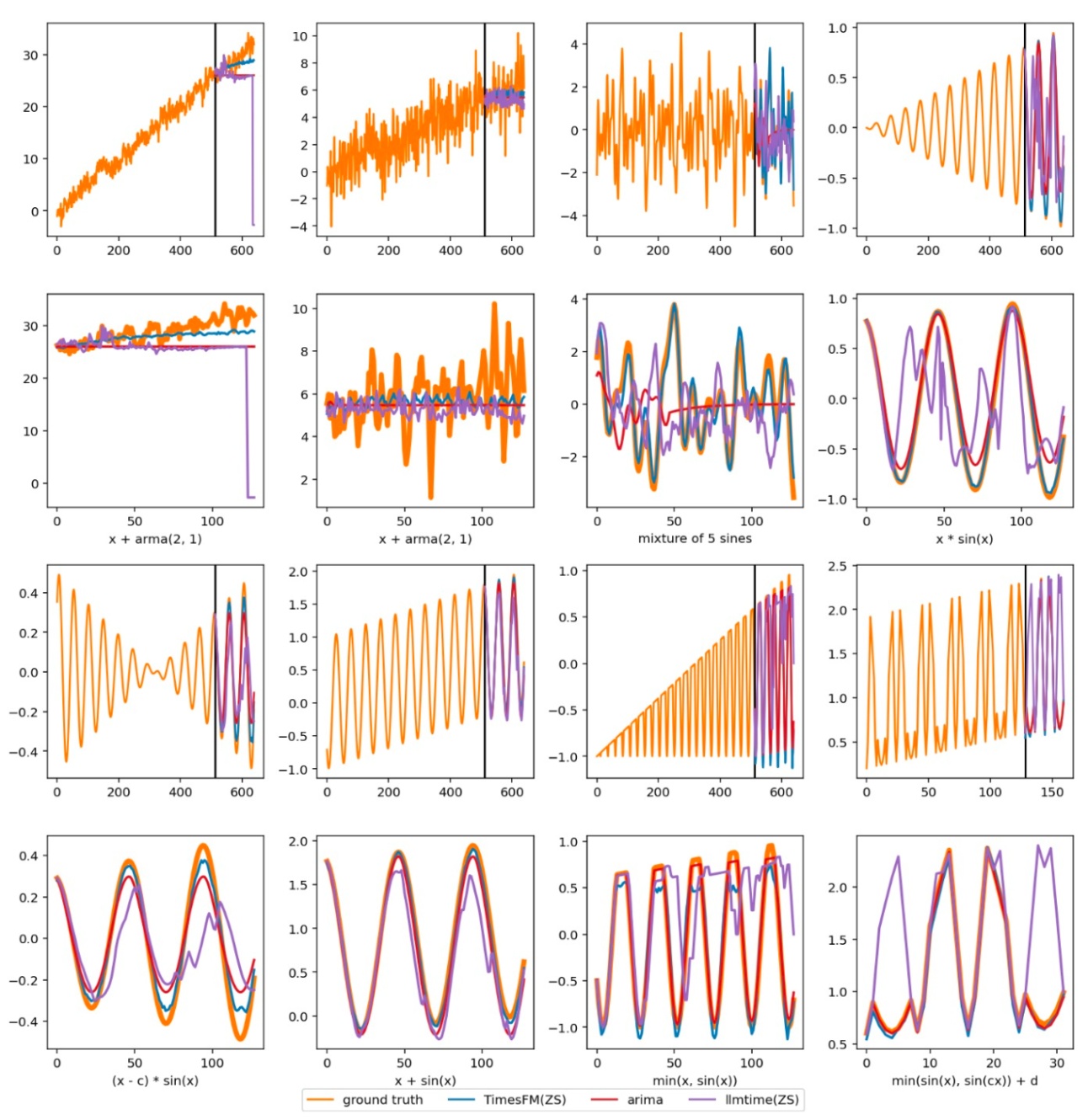
2, 4段目は1, 3段目の拡大版

まとめ

decoder onlyの時系列予測基盤モデルであるTimesFMの提案
合成データと組み合わせて学習することで汎化性能向上
LLM同様のスケーリングが確認できる

思ったこと

データセットの構成に関してもっとablationがあってもいいと思いました. 特に, 実データはgoogle trendsとwiki views以外のデータの影響が大きいように思えます.
技術的な新規性はあまりないように思えます. 先行研究の組み合わせでモデルを構築し, たくさんのデータで学習したにすぎません.
現状ではTransformerのdecoderのみで構成できるとLLMなどと合わせてMultimodalにしやすいと思うので, その点では好印象です.

参考文献

Abhimanyu Das, Weihao Kong, Andrew Leach, Shaan K Mathur, Rajat Sen, and Rose Yu. Long-term forecasting with tiDE: Time-series dense encoder. Transactions on Machine Learning Research, 2023.
Abhimanyu Das, Weihao Kong, Rajat Sen, and Yichen Zhou. A decoder-only foundation model for time-series forecasting. In Forty-first International Conference on Machine Learning, 2024.