Zenn
🚀

ABC228 D - Linear Probing C++解答例

2021/11/21に公開
C++
競技プログラミング
AtCoder
競プロ
tech

AtCoder Beginner Contest D - Linear ProbingをC++で解きます。

問題

問題文をAtCoderのページより引用します。

問題文

N = 2^{20}項からなる数列A = (A_0, A_1, \ldots, A_{N - 1})があります。はじめ、全ての要素は-1です。
Q個のクエリを順番に処理してください。i(1 \leq i \leq Q)個目のクエリはt_i = 1またはt_i = 2を満たす整数t_iおよび整数x_iで表され、内容は以下の通りです。

  • t_i = 1のとき、以下の処理を順番に行う。
    1. 整数hをh = x_iで定める
    2. A_{h \bmod N} \neq -1である間、hの値を1増やすことを繰り返す。この問題の制約下でこの操作が有限回で終了することは証明できる。
    3. A_{h \bmod N}の値をx_iで書き換える。
  • t_i = 2のとき、その時点でのA_{x_i \bmod N}の値を出力する。

なお、整数a, bに対し、aをbで割った余りをa \bmod bと表します。

制約

  • 1 \leq Q \leq 2 \times 10^5
  • t_i \in \{1, 2\} (1 \leq i \leq Q)
  • 0 \leq x_i \leq 10^{18} (1 \leq i \leq Q)
  • t_i = 2であるようなi(1 \leq i \leq Q)が1つ以上存在する。
  • 入力はすべて整数である。

解答例

計算量が大きいところ(高速化すべきところ)を見つける

クエリ処理の問題なので、問題文の通りに愚直に実装するとTLEになることは目に見えています。
高速化すべきところを探すところから始めます。

まず、N = 2^{20} \simeq 10^6なので、このサイズの配列を作ることは可能であることがわかります。
t_i = 2であるクエリ(以下、クエリ2と呼ぶことにします)は配列Aの要素の取得を要求してきますが、実際に配列を作ることができればこの処理は\mathcal{O}(1)で処理することができます。
したがって、高速化すべきクエリはt_i = 1のクエリ(以下、クエリ1と呼ぶことにします)であることが絞り込めます。

クエリ1の処理内容を見てみます。問題文を要約すると、

  • 配列Aにおけるインデックスがx_i \bmod Nである要素の値が-1なら、その要素の値をx_iで上書きする。
  • その要素の値が既に-1でない値で埋まっていたら、配列Aの値がまだ-1である要素のうち、インデックスがx_i \bmod Nより大きい要素の中で最小のインデックスを持つ要素の値をx_iで上書きする

という操作であることがわかります。
このクエリの中で、「値がまだ-1であり、かつインデックスがx_i \bmod Nより大きい配列Aの要素の中で、最小のインデックスを持つ要素」を探す処理が登場しています。
問題文の「A_{h \bmod N} \neq -1である間、hの値を1増やすことを繰り返す」は、この処理を愚直に行うことを意味しています。愚直にこの処理を行った場合、最悪の計算量は\mathcal{O}(N)であると予想できます。
この処理を高速化することができれば問題を解くことができそうです。

値が確定していない要素のインデックスを集合で管理する

便宜上、配列Aの要素のうち、値がまだ初期値(-1)である要素のことを、「値が確定していない要素」と呼ぶことにします。

「値が確定していない要素のうち、インデックスがh \bmod Nより大きい最小のインデックス」を求める処理は、C++のstd::setを使えば高速に処理することができます。

まだ値が確定していない要素のインデックスを集合の元として管理し、値が確定したら集合から削除します。
インデックスの検索処理は、std::setの二分探索メソッドであるlower_boundまたはupper_boundを用いることで高速に行うことができます。

インデックスを探すときの注意点

std::setの二分探索でインデックスを探す際の注意点として、x_i \bmod Nより大きいインデックスを持つ値の確定していない要素が存在しない場合を考えなければなりません。
例えば図で表すとこんな感じです。


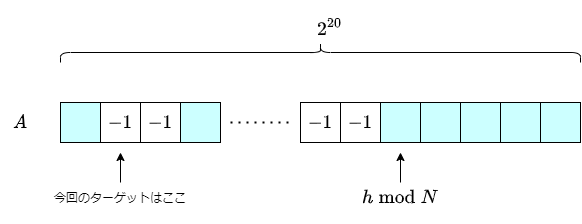
水色のマスは値が確定していることを表しています

あるクエリiに対して、h \bmod N以上のインデックスを持つ要素の値が全て確定していたとき、hを1ずつ増加させて初めてA_{h \bmod N} \neq -1になるのは、値が確定していない要素のうち一番若いインデックスを持つ要素となります。

したがって、二分探索の結果、要素が見つからなかったとき(lower_boundがstd::set::end()を返したとき)は、値が確定していない要素のうち一番若いインデックスを持つ要素をターゲットとして、その要素の値を書き換える必要があるということになります。

std::setは順序付き集合なので、「値が確定していない要素のうち一番若いインデックス」は、std::setの先頭に格納されているため。std::set::beginでアクセスすることができます。これを利用しましょう。

実装例

C++の実装例を以下に示します。

d.cpp
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
 
int main() {
  int64_t Q;
  std::cin >> Q;
  // クエリの受け取り
  std::vector<std::pair<int64_t, int64_t>> query(Q);
  for (int64_t i = 0; i < Q; i++) {
    int64_t t, x;
    std::cin >> t >> x;
 
    query.at(i) = std::make_pair(t, x);
  }
 
  int64_t N = 1 << 20;
  // 配列Aの各要素の初期値は-1
  std::vector<int64_t> A(N, -1);
  // 値が確定していない要素のインデックスを格納する集合
  std::set<int64_t> indexes;
  // 初期状態では全てのインデックスが集合に属している
  for (int64_t i = 0; i < N; i++) {
    indexes.insert(i);
  }
 
  // クエリ処理開始
  for (int64_t i = 0; i < Q; i++) {
    int64_t t = query.at(i).first;
    int64_t x = query.at(i).second;
 
    switch (t) {
      case 1:
        // A_{h mod N}の値が確定していないとき
        if (A.at(x % N) == -1) {
	  // そのまま値をxで上書きする
          A.at(x % N) = x;
	  // 値が確定した要素のインデックスは集合から削除する
          indexes.erase(x % N);
        } else {
	  // 二分探索によってターゲットのインデックスを探す
          auto iter = indexes.lower_bound(x % N);
 
          int64_t target_index;
	  // ターゲットが見つからなかったとき
          if (iter == indexes.end()) {
	    // 一番若いインデックスをターゲットとする
            target_index = *indexes.begin();
          } else {
	    // 見つかったらそれをターゲットとする
            target_index = *iter;
          }
 
          // 値をxで書き換える
          A.at(target_index) = x;
	  // 値が確定したので集合から削除する
          indexes.erase(target_index);
        }
 
        break;
      case 2:
        // 値の出力
        std::cout << A.at(x % N) << std::endl;
        break;
    }
  }
 
  return 0;
}

実際に提出したコードはこちら。

Discussion