Zenn
🕌

ABC221 D - Online Games C++解答例

2021/10/03に公開
C++
競技プログラミング
AtCoder
競プロ
tech

AtCoder Beginner Contest 221 D - Online GamesをC++で解きます。

問題

問題文をAtCoderのページより引用します。

問題文

あるオンラインゲームがあり、N人のプレイヤーが登録しています。
サービス開始日から10^{100}日を迎えた今日、開発者である高橋くんがログイン履歴を調べたところ、i番目のプレイヤーはサービス開始日を1日目として、A_{i}日めからB_{i}日間連続でログインし、それ以外の日はログインしていなかったことが判明しました。すなわち、i番目のプレイヤーはサービス開始日から、A_{i}, A_{i} + 1, \ldots, A_{i} + B_{i} - 1日目に、かつそれらの日にのみログインしていたことが分かりました。
1 \leq k \leq Nをみたす各整数kについて、サービス開始日から今日までの間で、ちょうどk人がログインしていた日数を答えてください。

制約

  • 1 \leq N \leq 2 \times 10^{5}
  • 1 \leq A_{i} \leq 10^9
  • 1 \leq B_{i} \leq 10^9
  • 入力はすべて整数である。

解答例

imos法を用い…れない

与えられた区間に1を足すというクエリがN個与えられ、ある日の値がk (1 \leq k \leq N)になるような日を数えるという問題なので、imos法を使いたくなります。

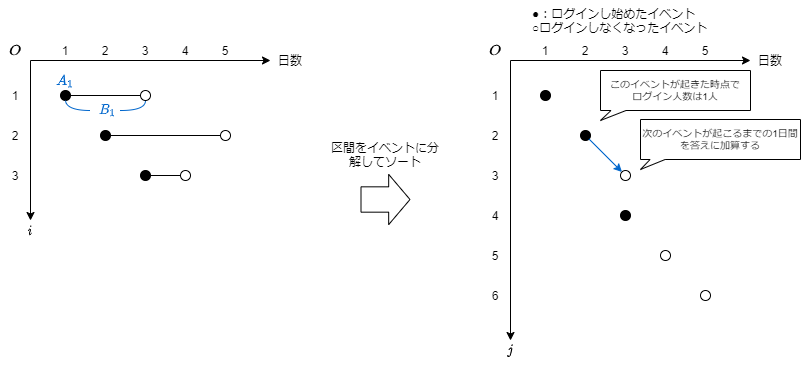
しかし制約を見ると、考慮しなければならない区間の最大幅は2 \times 10^9あります。imos法を使うには全ての日数に対するログイン人数の数を記録する配列を用意しなければなりませんが、2 \times 10^9個の要素を格納する配列を作るにはGB単位のメモリが必要となるため、使うことはできません。

イベントソートを使う

発想を変えてみます。あるプレイヤーiがログインし始めたのはA_{i}日目、ログインしなくなったのはA_{i} + B_{i}日目です。このことを、「A_{i}日目とA_{i} + B_{i}日目にイベントが発生した」と表現することとします。
ここで、「ログインし始めたときのイベント」と「ログインしなくなったときのイベント」は区別するものとします。

イベントをXとしたとき、あるi(1 \leq i \leq N)について発生するイベントをxとすると、x = A_{i}およびx = A_{i} + B_{i}の2通りとなります。
全てのiについて発生するイベントを配列としてまとめ、日時について昇順にソートした配列をX = (X_{1}, X_{2}, X_{3}, \ldots, X_{L})とします。ただし、L = 2Nです[1]。

あるイベントX_{j} (1 \leq j \leq L)が起きたとき、そのイベントが「誰かがログインし始めたイベント」ならば、次のイベントX_{j + 1}が発生するまでの(X_{j + 1} - X_{j})日間、ゲームにログインしている人数は一定であり、その人数は「イベントX_{j}が発生する直前までゲームにログインしていた人数 + 1」であることが分かります。
同様に、イベントX_{j}が「誰かがログインしなくなったイベント」ならば、次のイベントが発生するまでの(X_{j + 1} - X_{j})日間にゲームにログインしている人数は「イベントX_{j}が発生する直前までゲームにログインしていた人数 - 1」となります。

ここで、全てのiについてA_{i} < A_{i} + B_{i}なので、最初に起こるイベントX_{1}は必ず誰かがログインし始めたイベントであり、最後に起こるイベントX_{L}は最後に残った誰かがログインしなくなったイベントとなります。
従って、「イベントX_{1}が起きる以前の期間」および「イベントX_{L}が起きた後の期間」は誰もログインしていない状態となります。
この問題ではログイン人数が0のときの日数は求められていないため、これらの期間は考慮しなくても良いことになります。

まとめると、現在のログイン人数をカウントしておくカウンタ変数\text{count}と、答えを格納しておく配列\text{Ans}[k] (1 \leq k \leq N)を用意した上で、発生が早い順にイベントを見ていき、次のように計算していけば良いことになります。

  • イベントX_{j}がどちらのイベントかを確認する
    • 「ログインし始めたイベント」のとき：カウンタ変数をインクリメントする
    • 「ログインしなくなったイベント」のとき：カウンタ変数をデクリメントする
  • 今、カウンタ変数\text{count}には「イベントX_{j}が起きたときの現在のログイン人数」が格納されているので、次にイベントが起こるまでの日数(X_{j + 1} - X_{j})日を\text{Ans}[\text{count}]に足す

プログラムの実装例

実際にプログラムとして実装するときは、イベントを格納する配列をstd::vector<std::pair<int64_t, int64_t>>型配列として定義しておきます。
ペアの内容は、{イベントが発生した日時、人数の変化}とします。人数の変化はそのイベントが「ログインし始めたイベント」なら1、「ログインしなくなったイベント」なら-1です。

d.cpp
#include <iostream>
#include <vector>
#include <algorithm>

int main() {
  int64_t N;
  std::cin >> N;
  std::vector<std::pair<int64_t, int64_t>> X;
  for (int64_t i = 0; i < N; i++) {
    int64_t a, b;
    std::cin >> a >> b;
    X.push_back(std::make_pair(a, 1));  // ログインし始めたイベント
    X.push_back(std::make_pair(a + b, -1));  // ログインしなくなったイベント
  }

  // 発生する日時が早い順にソート
  std::sort(X.begin(), X.end());

  // 答えを格納しておく配列
  std::vector<int64_t> answer(N + 1, 0);
  // 現在のログイン人数をカウントしておくカウンタ変数
  int64_t count = 0;
  // 発生が早い順にイベントを見ていく
  for (int64_t i = 0; i < static_cast<int64_t>(X.size()) - 1; i++) {
    // イベントXiが起きたときのログイン人数を更新
    count += X.at(i).second;
    // 次にイベントが起きるまでの日数を答えに加算
    answer.at(count) += X.at(i + 1).first - X.at(i).first;
  }

  // 答えの出力
  for (int64_t i = 1; i <= N; i++) {
    if (i != 1) std::cout << " ";
    std::cout << answer.at(i);
  }
  std::cout << std::endl;

  return 0;
}

実際に提出したコードはこちら。

脚注

  1. あるiについてイベントは2回発生するため、イベントの数は2N個となります ↩︎

Discussion