ABC263 D - Left Right Operation Python解答例

AtCoder Beginner Contest 263 D - Left Right OperationをPythonで解きます。

問題

問題文をAtCoderのページより引用します。

問題文

長さ$N$の整数列$A=(A_1,A_2,\ldots,A_N)$が与えられます。

あなたは以下の連続する操作をちょうど一度だけ行います。

• 整数$x\ (0\leq x \leq N)$を選ぶ。$x$として$0$を選んだ場合何もしない。$x$として$1$以上の整数を選んだ場合、$A_1,A_2,\ldots,A_x$をそれぞれ$L$で置き換える。
• 整数$y\ (0\leq y \leq N)$を選ぶ。$y$として$0$を選んだ場合何もしない。$y$として$1$以上の整数を選んだ場合、$A_{N},A_{N-1},\ldots,A_{N-y+1}$をそれぞれ$R$で置き換える。

操作後の$A$の要素の総和として考えられる最小値を求めてください。

制約

• $1 \leq N \leq 2\times 10^5$
• $-10^9 \leq L, R\leq 10^9$
• $-10^9 \leq A_i\leq 10^9$
• 入力は全て整数

解答例

セグメント木で高速化

$A = (A_1, A_2, \ldots, A_N)$、$0 \leq x \leq N$、$0 \leq y \leq N$について、求める解は以下の図に示す3つの区間の総和の最小値であり、

$$\min_{0 \leq x \leq y \leq N} (Lx + \sum_{i=x + 1}^{N - y} A_i + Ry)$$

となります。

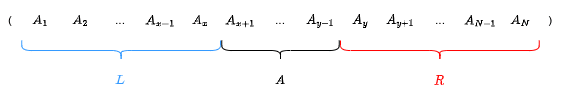
簡単のため、$N - y = y$とおきます^[1]。
また、配列$A$の累積和を$C_k = \sum_{i = 1}^{k} A_i$とおくと、総和記号を$\sum_{i = a}^{b} = C_{b} - C_{a - 1}$と書き換えられるので、

$$\begin{align*} \min_{0 \leq x \leq y \leq N} (Lx + \sum_{i=x + 1}^{y} A_i + R(N - y)) &= \min_{0 \leq x \leq y \leq N} (Lx + C_y - C_x + R(N - y)) \\ &= RN + \min_{0 \leq x \leq y \leq N} ((Lx - C_x) + (C_y + Ry)) \\ &= RN + \min_{0 \leq x \leq N} ((Lx - C_x) + \min_{x \leq y \leq N}(C_y + Ry)) \\ \end{align*}$$

と変形できます^[2]。
ここで、$\min_{x \leq y \leq N}(C_y + Ry)$の部分は、$0 \leq y \leq N$について、

$$D_y = \begin{cases} C_y - Ry & (1 \leq y \leq N) \\ 0 & (y = 0) \end{cases}$$

であるような配列$D$を考えたとき、区間の最小値を高速に求められるデータ構造を用いることで、各$x$について高速に求めることができます。
区間の最小値を高速に求めるデータ構造といえばセグメント木です。これを用いることで、各$x$について$\mathcal{O}(\log N)$で解を求められるので、全体で$\mathcal{O}(N\log{N})$の計算量で解を求めることができます。

実装例

Pythonのコード例を以下に示します。
上述した考察は1-indexedで考えられている一方で、プログラムでは0-indexedで考えなければならないことに注意します。

d.py

from typing import (
    List,
    TypeVar,
    Callable,
    Generic,
    Iterator,
    Union,
)
import sys
import itertools

sys.setrecursionlimit(1000000)
input = sys.stdin.readline

### セグメント木のクラス実装は長いので省略

def main():
    # 入力受け取り
    N, L, R = map(int, input().split())
    A: List[int] = list(map(int, input().split()))

    # Aの総和(x, yともに0のときの答え)を求める
    S: int = sum(A)
    # 累積和を求める。1-indexedにしておくと何かと便利だったりする
    C: List[int] = [0] + list(itertools.accumulate(A))
    # 配列Dを計算する。こちらも1-indexed。
    D: List[int] = [C[y] - R * y for y in range(N + 1)]

    # 配列Dをもとに区間最小を求めるセグメント木を構築する。
    seg = SegmentTree[int](min, lambda: 1 << 60, D)

    # 各xについて値を計算し、最小値を求める。
    answer: int = S
    for x in range(N + 1):
        answer = min(answer, R * N + L * x - C[x] + seg[x : N + 1])

    # 答えの出力
    print(answer)


if __name__ == "__main__":
    main()

実際の提出はこちら^[3]。

脚注

1. $N - y = y$と置き換えても$y$の範囲は$0 \leq y \leq N$のままです。

2. 問題で定義されている操作の順番より、右と左で重複した区間は考慮しなくても良いので、$x$を固定したときの$y$の範囲は$x \leq y \leq N$となります。

3. 各$x$について答えを求めるとき、for文を回しながら最小値を取得する方法の他、リスト内包表記を用いてワンライナーで書く方法もあります。こっちの方がPythonっぽくて好き。