Zenn
💬

ABC 218 C - Shapes C++解答例

2021/09/12に公開
C++
AtCoder
#
競プロ
tech

AtCoder Beginner Contest 218 C-ShapesをC++で解きます。

問題

問題文をAtCoderのページより引用します。

問題文

2次元グリッド上に2つの図形SとTがあります。グリッドは正方形のマスからなります。

SはN行N列のグリッド内にあり、S_{i, j}が#であるようなマス全体からなります。
TもN行N列のグリッド内にあり、T_{i, j}が#であるようなマス全体からなります。

SとTを 90度回転及び平行移動の繰り返しによって一致させることができるか判定してください。

制約

  • 1 \leq N \leq 200
  • S, Tは#と.のみからなる
  • S, Tは1つ以上#を含む

解答例

考え方

解き方の方針を決める

平行移動と回転移動の2つの操作を同時に考えるのは難しいです。幸い、平行移動と回転移動は独立して考えることができるので、回転と移動を分けて考える方針で行きます。

公式解説では、グリッド全体を回転させた後、平行移動によって図形が一致するかどうかをチェックすることで解いています。

私は公式解説のやり方がよく理解できなかったので、本記事ではグリッドから図形を切り出した後、片方の図形を回転させて一致するかどうかをチェックする方針で行きます。

図形を切り出すと平行移動は考えなくてよくなる

図形SとTのそれぞれについて、N \times Nのグリッドから図形が含まれている矩形のみを切り出すことを考えます。
図形が含まれている矩形のみを切り出してしまえば、グリッド上での平行移動を考える必要はなくなります。従って、4パターンの回転のみをチェックすることで問題を解くことができるようになります。

実装方法

方針に沿ってプログラムを実装していきます。
プログラム全体の流れは以下のようになります。

  1. 与えられたグリッドから図形SとTを切り出す。
  2. 2つの図形が等しいかどうか判定する。
  3. Tを回転させる。
  4. 2.と3.を4回繰り返す

切り出し、判定、回転の操作は複数回行うので、関数として実装しておきます。

図形を切り出す関数

まずは与えられたグリッドから図形を含む矩形を切り出す関数を実装します。
図形を含む矩形を切り出すには、「#セルが存在する行のうち一番上の行」「#セルが存在する行のうち一番下の行」「#セルが存在する列のうち一番下の列」「#セルが存在する列のうち一番下の列」の4つの情報が必要となります。

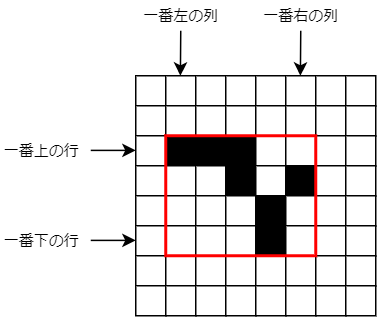
これを求めるには与えられたグリッドを走査していき、それぞれの情報を変数にとってstd::minとstd::maxを活用して行けば良いです。
あとはこれらの情報を元にグリッドを切り出し、図形を返します。

図形を切り出す関数
std::vector<std::string> trim(std::vector<std::string> X) {
  int64_t N = static_cast<int64_t>(X.size());
  int64_t min_r = 1LL << 60;
  int64_t max_r = 0;
  int64_t min_c = 1LL << 60;
  int64_t max_c = 0;
  for (int64_t i = 0; i < N; i++) {
    for (int64_t j = 0; j < N; j++) {
      if (X.at(i).at(j) == '#') {
        min_r = std::min(min_r, i);
        max_r = std::max(max_r, i);
        min_c = std::min(min_c, j);
        max_c = std::max(max_c, j);
      }
    }
  }
  std::vector<std::string> trimed_X;
  for (int64_t i = min_r; i <= max_r; i++) {
    trimed_X.push_back(X.at(i).substr(min_c, max_c - min_c + 1));
  }

  return trimed_X;
}

図形を回転させる関数

次に図形を回転させる関数を実装します。この問題では90°毎の回転のみ考慮すればいいので、右か左のどちらかに90°回転させる関数を1つ実装すれば事足ります。

図形を回転させる関数
std::vector<std::string> rotate(std::vector<std::string> X) {
  int64_t H = static_cast<int64_t>(X.size());
  int64_t W = static_cast<int64_t>(X.at(0).size());

  std::vector<std::string> x(W);
  for (int64_t i = 0; i < W; i++) {
    for (int64_t j = H - 1; j >= 0; j--) {
      x.at(i).push_back(X.at(j).at(i));
    }
  }

  return x;
}

2つの図形が一致しているかどうか判定する関数

次に、2つの図形が一致しているかどうかを判定する関数を実装します。
この関数の処理は単純で、各図形のセルが一致しているかどうかを全てのセルについて走査するだけです。
また、図形が一致するためには図形のサイズが合っていることが前提なので、前処理としてその判定も行っています。

2つの図形が一致しているかどうか判定する関数
bool is_same(std::vector<std::string> S, std::vector<std::string> T) {
  if (S.size() == T.size() && S.at(0).size() == T.at(0).size())
  {
    bool ok = true;
    for (size_t i = 0; i < S.size(); i++) {
      for (size_t j = 0; j < S.at(0).size(); j++) {
        if (S.at(i).at(j) != T.at(i).at(j)) ok = false;
      }
    }
    return ok;
  } else {
    return false;
  }
}

提出したコード

以上を踏まえたコード全体を以下に示します。

制約を見ると、N = 1が入力として与えられる場合が存在することが分かります。N = 1のときこれらの関数はうまく動作しないので、例外の処理をmain関数の最初の方で行っています。
N = 1のとき、制約より両者のグリッドは#が1つのみになるので、Yesを出力します。[1]

また、グリッドからそれぞれの図形を切り出した後、図形のサイズが両者で異なっていた場合の処理も入れ込んでいます。回転させても図形のサイズが異なっているならば明らかに図形は一致しないためです。

コード全体
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>

std::vector<std::string> trim(std::vector<std::string> X) {
  int64_t N = static_cast<int64_t>(X.size());
  int64_t min_r = 1LL << 60;
  int64_t max_r = 0;
  int64_t min_c = 1LL << 60;
  int64_t max_c = 0;
  for (int64_t i = 0; i < N; i++) {
    for (int64_t j = 0; j < N; j++) {
      if (X.at(i).at(j) == '#') {
        min_r = std::min(min_r, i);
        max_r = std::max(max_r, i);
        min_c = std::min(min_c, j);
        max_c = std::max(max_c, j);
      }
    }
  }
  std::vector<std::string> trimed_X;
  for (int64_t i = min_r; i <= max_r; i++) {
    trimed_X.push_back(X.at(i).substr(min_c, max_c - min_c + 1));
  }

  return trimed_X;
}

std::vector<std::string> rotate(std::vector<std::string> X) {
  int64_t H = static_cast<int64_t>(X.size());
  int64_t W = static_cast<int64_t>(X.at(0).size());

  std::vector<std::string> x(W);
  for (int64_t i = 0; i < W; i++) {
    for (int64_t j = H - 1; j >= 0; j--) {
      x.at(i).push_back(X.at(j).at(i));
    }
  }

  return x;
}

bool is_same(std::vector<std::string> S, std::vector<std::string> T) {
  if (S.size() == T.size() && S.at(0).size() == T.at(0).size())
  {
    bool ok = true;
    for (size_t i = 0; i < S.size(); i++) {
      for (size_t j = 0; j < S.at(0).size(); j++) {
        if (S.at(i).at(j) != T.at(i).at(j)) ok = false;
      }
    }
    return ok;
  } else {
    return false;
  }
}

int main() {
  int64_t N;
  std::cin >> N;

  if (N == 1) {
    std::cout << "Yes" << std::endl;
    return 0;
  }

  std::vector<std::string> S(N);
  for (auto& s : S) {
    std::cin >> s;
  }
  std::vector<std::string> T(N);
  for (auto& t : T) {
    std::cin >> t;
  }

  auto s = trim(S);
  auto t = trim(T);

  bool ok = false;
  if ((s.size() == t.size() && s.at(0).size() == t.at(0).size())
      || (s.size() == t.at(0).size() && s.at(0).size() == t.size()))
  {
    for (int64_t i = 0; i < 4; i++) {
      t = rotate(t);
      if (is_same(s, t)) ok = true;
    }
  }

  if (ok) {
    std::cout << "Yes" << std::endl;
  } else {
    std::cout << "No" << std::endl;
  }

  return 0;
}

実際に提出したコードはこちら。

脚注

  1. でも例外処理を省いたコードを提出してもREが出なかったのでテストケースには無かったっぽい ↩︎

Discussion