Pythonで実装する非再帰抽象化セグメント木

競技プログラミングでよく使われるデータ構造「セグメント木」をPythonで実装し、仕組みや実装方法を理解します。

セグメント木の概要

セグメント木とは

区間に対するクエリを高速に処理できるデータ構造の1つです。各ノードが区間に対応付けられた完全二分木として表現されます。
根は区間全体を表し、各ノードの子は親の区間を二等分した区間を表現します。

具体的には、以下のようなクエリを$\mathcal{O}(\log{N})$で処理することができます。

• $i$番目の要素の値を取得する
• $i$番目の要素を任意の値で更新する
• 区間$[l, r)$に対する演算結果を求める

セグメント木の構成要素

セグメント木は以下の要素から成ります。

• 区間の要素の型$S$
• 二項演算子$\bullet: S \times S \rightarrow S$

例えば区間最小値を求めるRange Minimum Query問題では、要素の型はintで、二項演算子はmin()が当てはまります。
区間和を求める問題では、二項演算子は足し算になります。

どんな型と二項演算子でも適用できるわけではなく、これらはモノイドを成していなければなりません。
モノイドの定義は以下です：

---

集合$S$とその上の二項演算$\bullet: S \times S \rightarrow S$、および$S$に属する単位元$e$が、以下の条件を満たすとき、組$(S, \bullet, e)$をモノイドという。

• 結合律：$S$の任意の元$a, b, c \in S$に対して、$(a \bullet b) \bullet c = a \bullet (b \bullet c)$が成り立つ。
• 単位元律：任意の$a \in S$に対して、$a \bullet e = e \bullet a = a$を満たす$e$が存在する。

---

ざっくり言い換えると、「演算の順番で結果が変わらない」「演算しても値が変わらないような値が存在する」を満たしていればセグメント木に乗せることができます。
例えば、整数同士の掛け算を考えると、

• 集合$S$は整数の集合$\mathbb{Z}$
• 二項演算子$\bullet$は掛け算$\times$
• 単位元は$1$

となり、組$(\mathbb{Z}, \times, 1)$はモノイドです。

競技プログラミングでは大抵の場合、集合$S$は整数集合$\mathbb{Z}$です。^[1]
二項演算子としては以下のものをよく使います。

演算	単位元	対応するPython関数
和	0	operator.add
積	1	operator.mul
最小値	$+\infty$	min
最大値	$-\infty$	max
論理和	0	operator.or_
論理積	1	operator.and_
排他的論理和	0	operator.xor
最大公約数	0	math.gcd
最小公倍数	1	math.lcm(Python3.9以降)

尚、二項演算の結果を積と呼びます。

実装

ここからはセグメント木の実装をするための仕様やデータ表現方法を決定します。

セグメント木に対する操作の定義

本記事で実装するセグメント木は、以下の操作を受け付けることを想定します。

1. 構築：クエリの対象となるリスト$A = (a_0, a_1, \ldots, a_{N-1})$を渡し、セグメント木を構築する。
2. 点取得：$k$番目の要素の値を取得する。
3. 点更新：$k$番目の要素を任意の値で更新する。
4. 区間取得：区間$[l, r)$に対する二項演算の結果を取得する。

ここで、$0 \leq k < N, 0 \leq l < r < N, N = |A|$です。
セグメント木はクラスで実装するものとし、最初の操作はコンストラクタで、その他の操作はメソッドで行うものとします。

データの表現方法

セグメント木は完全二分木なので、1つのリストで表現することができます。
木を表現するリストの長さは、葉の数を$M$として$2M$です。

完全二分木であるので、葉の数は2のべき乗個である方が都合が良いです。
クエリ対象のリスト$A$の長さ$N$が2のべき乗でない場合は、「$N$以上の最小の2のべき乗」を葉の数$M$とします。

また、セグメント木を表すリストは1-indexedで実装します^[2]。つまり、根を表すノードはインデックスが1となります。
こうすることで、木のノードのインデックスに対する演算は以下のようになります。

• インデックス$k$のノードの左の子は$2k$のインデックスを持つ。
• インデックス$k$のノードの右の子は$2k + 1$のインデックスを持つ。
• インデックス$k$のノードの親は$\lfloor \frac{k}{2} \rfloor$のインデックスを持つ。
• リスト$A$の要素$a_i$に対応するノードのインデックスは$i + M$である。$(0 \leq i < N)$

これらを踏まえ、各操作を行うための処理を実装していきます。

操作1：セグメント木の構築

二項演算子$\bullet$、単位元$e$、リスト$A$を受け取り、セグメント木を構築します。
二項演算子と単位元は関数オブジェクトとして扱います。例えば二項演算子が最小値minの場合、以下のような関数を受け取ることになります^[3]。

二項演算子と単位元を表す関数

# 二項演算子
def op(a: S, b: S) -> S:
    return min(a, b)

# 単位元
def e() -> S:
    # 十分大きい整数で+∞を代用する。
    return 1 << 60

次に、リスト$A$の長さ$N$をもとに葉の数$M$を計算し、木を表現する長さ$2M$のリスト$D = (d_0, d_1, \ldots, d_M, d_{M + 1}, \ldots, d_{2M - 1})$を生成します。
葉の値はリスト$A$の値で初期化しておきます。リスト$A$の要素$a_i$に対応する$D$の要素は$d_{M + i}$で計算されるので、$D$のリストの区間$[d_M, d_{M + N})$を$A$の要素で上書きすれば良いです。
その他の要素は全て単位元$e$で初期化しておきます。

その後、$A$の値をもとに、葉以外のノードの値を更新します。更新は葉に近い側から根に向かって行います。
更新処理は後述します。

セグメント木の構築にかかる時間計算量は$\mathcal{O}(N\log{N})$です。

操作2：点取得

点取得の処理は簡単で、インデックス$k(0 \leq k < N)$に対して$D_{M + k}$を返すだけです。

操作3：点更新

ここからはノードの更新処理を実装していきます。

点更新を実装するために、まずは「子ノードの値をもとにノードの値を計算する処理」を考えます。
これは単純に、左右の子ノードの値に対して二項演算子opを適用するだけで良いです。左右の子にアクセスするにはそれぞれ$2k$、$2k + 1$を使えることを考えると、コードは以下のようになります。

D[k] = op(D[2 * k], D[2 * k + 1])

次に、ある葉の値を更新したときに、その値を各区間へ反映させることを考えます。
葉の値を更新したら、「その葉を含む区間」の値を更新しなければなりません。この区間は葉の親を順に辿っていくことで全て網羅することができます。

すなわち、値を更新した葉から根に向かって親へと辿って行き、各親について、子ノードの値を用いて値を更新していけばよいです。
このプロセスを図にすると、以下のようになります。

まず、葉の値を更新します。ここでは$a_4$に対応する葉(つまり$D_{12}$)の値を5に更新したとします。

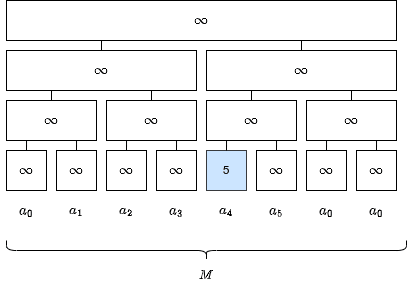
ここから、$D_{12}$から始めて順に親ノードを辿ります。$D_{12}$を子孫に持つノードは$D_{6}, D_{3}, D_{1}$の3つです。
これらを順に辿っていくには、インデックスを2で割り続ければよいです。
それぞれの親について値の更新処理をすることで、点更新処理を完了できます。

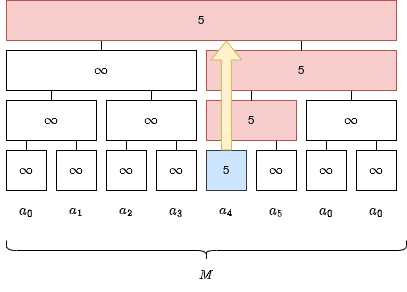
コードにすると以下のようになります。親を辿る際はビットシフトを用いると簡潔に書けます。

def update(k: int):
    D[k] = op(D[2 * k], D[2 * k + 1])

# k: 更新する葉のインデックス(0-indexed, 0 <= key < N)
# value: 更新する値

# 葉に移動する
k += M

# 葉の値を更新する
D[k] = value

# H: セグメント木の高さ
# M = 2 ^ H が成り立つ。
for i in range(1, H + 1):
    # k >> iとすることで、i世代前のkの親にアクセスできる
    update(k >> i)

操作4：区間取得

最後に、区間$[l, r)$に対する二項演算の積を求める処理を実装します。
この処理では、「指定された区間をカバーする全てのノードを見つけ出し、それぞれの値を集約する」手順をボトムアップで行います。

例として、$A = (3, 1, 5, 2, 10, 8)$に対するRange Minimum Queryを処理するセグメント木を考えてみます。
構築後の時点では、セグメント木は以下のような状態になっています。

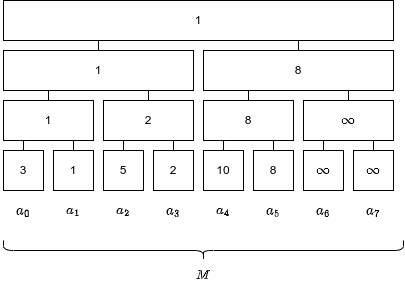
ここで、区間$[1, 6)$に対する積を求めることを考えます。

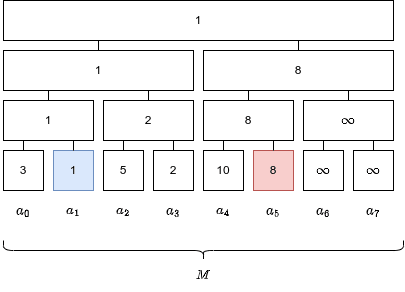
この区間$[1, 6)$の積を求めるためには$D_{9}, D_{10}, D_{11}, D_{12}, D_{13}$に対して二項演算子を適用した結果を求めれば良いわけですが、それでは計算効率が悪いです。
セグメント木を見ると、$D_{10} \bullet D{11}$の結果はすでに$D_{5}$に、$D_{12} \bullet D_{13}$の結果は$D_{6}$に、それぞれ格納されていることがわかります。

二項演算子$\bullet$については結合律が成り立つことが保証されているので、

$$\begin{align*} D_{9} \bullet D_{10} \bullet D_{11} \bullet D_{12} \bullet D_{13} &= D_{9} \bullet (D_{10} \bullet D_{11}) \bullet (D_{12} \bullet D_{13}) \\ &= D_{9} \bullet D_{5} \bullet D_{6} \end{align*}$$

が成り立ち、計算回数を減らすことができます。
適切なノードの組み合わせを選ぶことで、少ない計算回数で効率的に区間の積を求めることができるわけです。

では、このようなノードの組み合わせをどのように選択すればよいでしょうか？
結論から述べると、ノード$D_{M + l}$、および$D_{M + r}$がそれぞれ「右の子か、左の子か」を見ることで、選択すべきノードを決定することができます。

区間の左側のノード$D_{M + l}$について、以下のような条件分岐が考えられます。

• ノード$D_{M + l}$が右の子の場合、$D_{M + l}$の親は、$D_{M + l}$の弟を含んでしまっているので、選択するのは不適切となります。
  従って、ノード$D_{M + l}$を選択し、兄ノードに移動します。
• ノード$D_{M + l}$が左の子の場合、$D_{M + l}$の親は$D_{M + l}$の情報を完全に含むため、区間積の計算にはこれを使用すれば良いです。
  従って、ノード$D_{M + l}$は選択せず、その親を選択します。

区間の右側のノード$D_{M + r}$については、左側と逆の条件分岐になります。

• ノード$D_{M + r}$が右の子の場合、その親は$D_{M + r}$の情報を完全に含むため、区間積の計算にはそれを使用すれば良いです。
  従って、ノード$D_{M + r}$は選択せず、その親を選択します。
• ノード$D_{M + r}$が左の子の場合、その親は$D_{M + r}$の兄を含んでしまっているので、選択するのは不適切になります。
  従って、ノード$D_{M + r}$を選択し、弟ノードに移動します。

これらの条件分岐をしつつ、選択したノードの値について逐一積を計算しながら親へ親へと移動していきます。
全ての区間を網羅したときの積の結果が区間$[l, r)$の積となります。

ソースコード例

以上を踏まえて非再帰抽象化セグメント木を実装すると、以下のようになります。
Pythonクラスとして実装するにあたり、点取得・点更新は特殊メソッド__getitem__()、__setitem__()を使って実装するようにしています。
区間積の計算は、通常のメソッドとして実装した他、各括弧にスライスでアクセスしたときも同じ結果が返るようにしています。

使用例

セグメント木を用いていくつかの問題を解いてみます。

Aizu Online Judge DSL 2_A Range Minimum Query(RMQ)

典型的なセグメント木の使用例です。点更新と区間積を求める問題です。

dsl_2_a.py

from typing import (
    List,
    TypeVar,
    Callable,
    Generic,
    Iterator,
    Union,
)

# セグメント木のクラス実装は省略

def main():
    N, Q = map(int, input().split())
    query = [list(map(int, input().split())) for i in range(Q)]

    seg = SegmentTree[int](
        lambda a, b: min(a, b), lambda: (1 << 31) - 1, [(1 << 31) - 1] * N
    )

    for t, x, y in query:
        if t == 0:
            seg[x] = y
        else:
            print(seg[x : y + 1])


if __name__ == "__main__":
    main()

実際の提出はこちら。

Aizu Online Judge DSL 2_B Range Sum Query(RSQ)

こちらも典型です。点取得、点更新、および区間積の操作が必要となります。
なぜか入力が1-indexedで与えられるので注意です。

dsl_2_b.py

from typing import (
    List,
    TypeVar,
    Callable,
    Generic,
    Iterator,
    Union,
)

# セグメント木のクラス実装は省略

def main():
    N, Q = map(int, input().split())
    query = [list(map(int, input().split())) for i in range(Q)]

    seg = SegmentTree[int](lambda a, b: a + b, lambda: 0, [0] * N)

    for t, x, y in query:
        if t == 0:
            x -= 1
            seg[x] = seg[x] + y
        else:
            x -= 1
            y -= 1
            print(seg[x : y + 1])


if __name__ == "__main__":
    main()

実際の提出はこちら。

2023/12/09 追記

• 「右側の結果を計算していく箇所、right_result = self._op(right_result, self._data[r])では可換性を求められるのでは？」という指摘があり、確かにその通りだったのでコードを修正しました。
• 使用例も修正後の実装で提出したものに差し替えました。

参考文献

• セグメント木を徹底解説！0から遅延評価やモノイドまで - アルゴリズムロジック
• セグメント木を使う - Zenn
• セグメント木をソラで書きたいあなたに hogecoder
• セグメント木を一歩一歩実装して理解しようとする(python) - Qiita
• プログラミングコンテストでのデータ構造 - slideshare
• 競技プログラミングノート セグメント木 - Read the Docs
• モノイド - Wikipedia

脚注

1. 遅延セグメント木においては、区間和などの区間の長さの情報が必要となる演算を行う場合は、整数値と区間の長さをメンバに持つクラスを要素の型とすることがあります。通常のセグメント木では整数型しか使わない気がします(あんまり自信無いけど)

2. セグメント木に対する操作では0-indexedで受け付けますが、内部実装は1-indexedとします。この方がすっきりした実装になるという理由でこのようにしています。

3. 組み込み関数minをそのまま渡しても良いです。(むしろそっちの方がパフォーマンスでるのかも…？)