gpt-2からgpt-ossへの進化をモデル構造から読む
はじめに
こんにちは。ナウキャストでデータエンジニア/LLMエンジニアとして頑張っているTakumiです。
2025年8月5日 OpenAIがオープンウェイトモデルとしてgpt-ossを発表しました。
OpenAIが発表した大規模言語モデルとしては、gpt-2以来のオープンウェイトモデルとなります。
ベンチマークの結果等から、既存のモデルと同等ないしは上回るの能力を持っているgpt-ossですが、gpt-2と何が変わったのでしょうか?
Github Repositoryのコードを読んで、モデル構造の観点からgpt-2とgpt-ossを比較してみます。
※この記事では、比較対象としてgpt-oss 20Bとgpt-2を選択しています。
参照リポジトリ
この記事では、gpt-2 XLarge, gpt-oss 20Bを比較対象としています。
-
gpt-2
https://github.com/huggingface/transformers/blob/v4.56.0/src/transformers/models/gpt2/modeling_gpt2.py
https://github.com/openai/gpt-2
定量的な違い
まず、パラメータ数等の定量的な違いを見ていきましょう。
| モデル名 | 最大入力トークン数 | 最大出力トークン数 | モデルパラメータ数 | 埋め込み次元 | 層数 | アテンションヘッド数 | モデルサイズ |
|---|---|---|---|---|---|---|---|
| gpt-2 XL | 1,024 | 1,024 | 1.5B | 1,600 | 48 | 25 | 約6.2GB |
| gpt-oss-20b | 131,072 | 131,072 | 21.5B | 2,880 | 24 | 64 | 約12.8GB |
こう比較してみるとモデルパラメータの増加の割に、モデルサイズの増加が抑えられています。
何より最大入出力トークンの伸びがすごいですね。
モデル構造
全体像を見てみよう
以下はコードから読み解いたモデル構造の全体像です。

図から、全体の流れとしては大きく変化しておらず、各ブロックが進化していることがわかります。
各ブロックがどの様に変化しているのか見ていきます。
Tokenizing Text
gpt-2, gpt-ossではどちらもByte-Pair Encoding(以下、BPE)を行っています。概念図は以下の通りです。

やっていることはあまり変わってないですが、語彙数、分割単位等が変化しています。
| 観点 | gpt-2 (2019) | o200k_harmony (2025, gpt-oss採用) |
|---|---|---|
| 方式 | Byte-level BPE | BPEベース(o200k_baseの上位互換, Harmony拡張) |
| 語彙数 | 50,257 | 201,088 |
| 基底単位 | 256バイト(どんな文字列も可逆に扱える) | 同様にバイト基盤だが、事前分割規則を強化(数字・記号・多言語対応) |
| 分割単位 | サブワード(例: “playing” → “play”, “ing”) | サブワード + 特殊記号 + 会話用メタトークン |
| 特別トークン | <|endoftext|> |
<|system|>, <|user|>, <|assistant|>,<|analysis|> , <|call|> , <|return|> など多数 |
| 得意分野 | 一般英語テキスト | 英語+コード・数式・記号・数字列、会話構造の保持 |
| 圧縮効率 | トークンが細かくなりがち(文章が長いと増える) | 頻出パターンや数字列をまとめて1トークン化 → 同じ文章でも短くなる傾向 |
これをみると、新しいEncodingではインタラクティブなやり取りやCoT、ツール呼び出しなどを想定したものになっていることがわかります。
補足
実際に以下のコードでどういうsubwordに分けることができるか、どういうIDがつくのかを確認しました。
import tiktoken
text = "This is a pen."
# gpt-2
enc_gpt2 = tiktoken.get_encoding("gpt2")
ids_gpt2 = enc_gpt2.encode(text)
print("=== gpt-2 ===")
print("Tokens:", [enc_gpt2.decode([i]) for i in ids_gpt2])
print("IDs:", ids_gpt2)
# o200k_harmony
enc_o200k = tiktoken.get_encoding("o200k_harmony")
ids_o200k = enc_o200k.encode(text, allowed_special="all")
print("\n=== o200k_harmony ===")
print("Tokens:", [enc_o200k.decode([i]) for i in ids_o200k])
print("IDs:", ids_o200k)
output
=== gpt-2 ===
Tokens: ['This', ' is', ' a', ' pen', '.']
IDs: [1212, 318, 257, 3112, 13]
=== o200k_harmony ===
Tokens: ['This', ' is', ' a', ' pen', '.']
IDs: [2500, 382, 261, 6022, 13]
ちなみにgpt-2時代のencodingだと、日本語が文字化けしました。
=== gpt-2 ===
Tokens: ['大', '�', '�', '�', '�', '�', '�', '�', '�']
IDs: [32014, 33768, 98, 17312, 105, 30585, 251, 32368, 121]
=== o200k_harmony ===
Tokens: ['大', '日本', '帝', '国']
IDs: [1640, 9048, 67888, 3052]
Positional Encodingの手法と処理
Positional Encodingの違いについて説明します。
絶対位置エンコーディング
gpt-2では、絶対位置エンコーディング を採用していました。特定の位置に対して、どの様な埋め込みを計算すればいいのかを大量のデータから学習する手法です。
イメージは、
- テキストから各トークンの位置を取得
def positions_for(tokens, past_length):
batch_size = tf.shape(tokens)[0]
nsteps = tf.shape(tokens)[1]
return expand_tile(past_length + tf.range(nsteps), batch_size)
- 位置から埋め込みベクトルを取得(学習可能なベクトル)
wpe = tf.get_variable('wpe', [hparams.n_ctx, hparams.n_embd],
initializer=tf.random_normal_initializer(stddev=0.01))
- token embeddingsとpositional embeddingsの加算結合
h = tf.gather(wte, X) + tf.gather(wpe, positions_for(X, past_length))
みたいなイメージです。
この手法だと位置ごとに独立している状態なので、相対関係(トークン間の距離関係)が考慮できない状態になっていました。
Transformerの原論文 では、sin/cosを使った位置埋め込みが採用されていました。絶対位置エンコーディングとしては同じです。
ここの違いは、
- Transformerは機械翻訳が元のターゲットであり、翻訳では系列長が入力によって変化するのでsin/cosを使って固定されたエンコーディングを用いることで汎化性能を狙った。
- gpt-2は言語モデルであり、 学習と推論で「最大系列長(1024トークン)」をあらかじめ固定して、それを超える外挿は想定しない。したがって変換方法を学習することで柔軟性を狙った。
という目的の違いから発生したのかなと思っています。
RoPE(Rotary Positional Encoding)
gpt-ossでは相対位置エンコーディングを採用しており、具体的な手法としてRoPEを使っています。
RoFormer: Enhanced Transformer with Rotary Position Embeddingという論文で提唱された手法でAttention内に相対位置表現を取り込むために提唱されました。
具体的には、AttentionのQuery, Keyに対して回転操作を行うことで相対的なトークン間の相対的な位置表現を保存しています。
1. RoPE の適用
埋め込みベクトル
ここで
2. Attention における性質
RoPE を適用した Query
すなわち、注意スコアが位置差
Attention 計算に 相対位置情報が自然に組み込まれる。
すなわち、内積が位置差
これにより 相対位置情報が Attention 計算に組み込まれる。
YaRN拡張(Yet another RoPE extentioN)
ここまでで、学習した範囲について相対的な位置を考慮することができました。一方でRoPEをそのまま使うと、訓練で扱ったものより長いコンテキストについて著しく性能が落ちてしまいます。
先ほどの式で言うと、θが高周波となり回転し過ぎてしまうことでその性能劣化が発生します。
そこで、YaRN では、位置
スケーリング関数
-
L_{train} -
\alpha, \beta
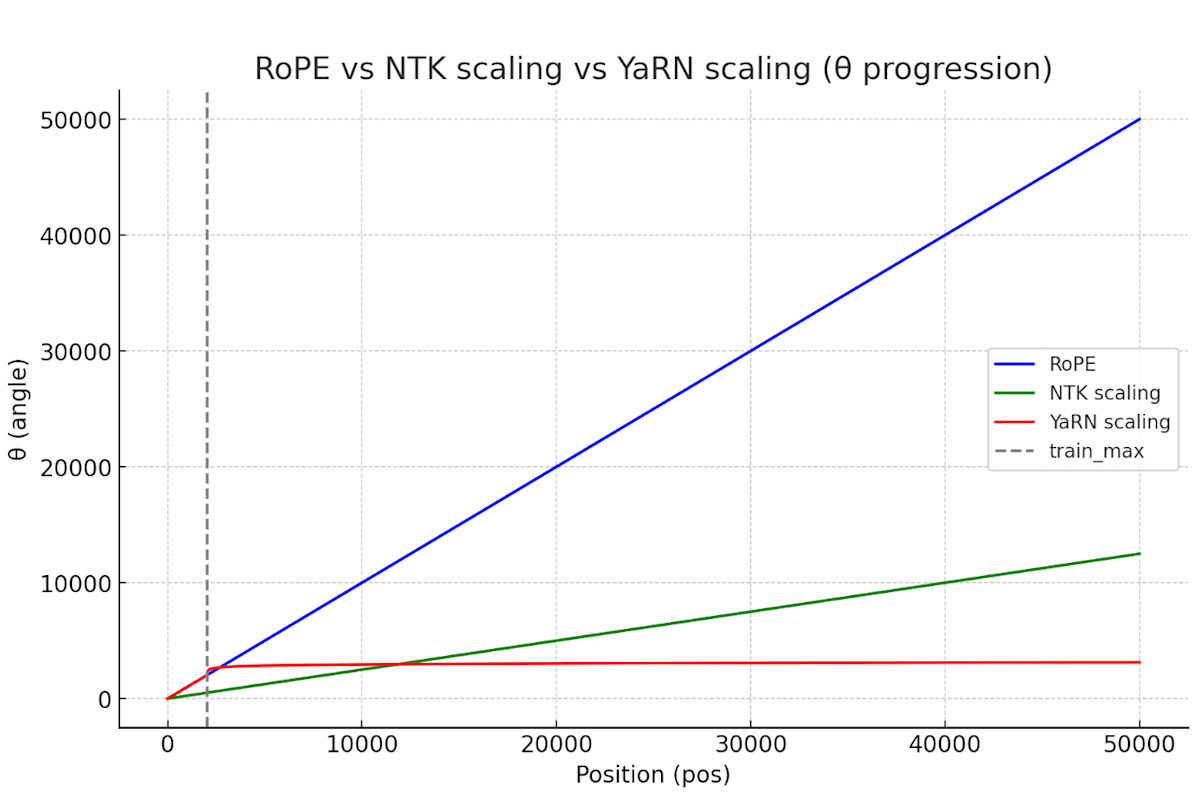
この形も持っていくことで以下の図の様に、学習の範囲ではRoPEと同じ振る舞いをして、学習の範囲外ではPositionをスケーリングすることができます(相対的な位置関係が変化し過ぎない。)。
DropOutの削除
Transformer 論文でのDropOut
Attention Is All You Need (Vaswani et al., 2017) では、以下のように DropOut の使用が明記されています。
Residual Dropout We apply dropout [33] to the output of each sub-layer, before it is added to the sub-layer input and normalized. In addition, we apply dropout to the sums of the embeddings and the positional encodings in both the encoder and decoder stacks. For the base model, we use a rate of Pdrop = 0.1.
つまり、各サブレイヤー(Self-Attention や MLP)の出力や、入力埋め込み+位置エンコーディングの和に対して 残差接続の直前で DropOut (p=0.1) が適用されていました。
gpt-2でのDropout導入とgpt-ossでの削除
One Epoch Is All You Need. では、gptは100 epoch, (情報ソースがないですが)gpt-2では20 ~ 100 epochだった可能性があると言及しています。一方で、gpt-2を再現したDiscussionではcheckpointのvalidation errorに1 epochで届いていることから、そもそも1poch(ないしは数epoch)しか学習していないとも考えられます。
想像でしかないですが、Transformerを取り入れる過程で残っただけに見えますね。
gpt-ossでDropoutがない理由
Llamaの論文でEpoch数について言及がありました。
Overall, our entire training dataset contains roughly 1.4T tokens after tokenization. For most of our training data, each token is used only once during training, with the exception of the Wikipedia and Books domains, over which we perform approximately two epochs.
特定のドメインを除くデータセットについては1回だけ訓練過程で使用している様です。(これは、ある程度信用できる情報については2回見せてる??)そもそも、Billion、Trillion単位のパラメータを持つ大規模モデルは1回データを見せれば、バックプロパゲーションでパラメータに反映できてしまうのかもしれません。DropOutは学習時に一部ユニットをランダムで無効化するので、1epochしか回さないのであればむしろ逆効果になることから削除されたのでしょう。
Normalization
Layer Normalization
gpt-2では以下の式で表されるLayer Normalizationが使われています。
ここでは、平均と分散を使って入力を正規化していて出力は0を平均とした分布になります。
ここで
Root Mean Squared(RMS) Normalization
一方でgpt-ossではRoot Mean Squared Normalizationが使われています。
こちらは、2乗平均平方根のみを使って正規化を行っています。こちらは平均は保存されて単にスケーリングをしています。
なぜgpt-ossではRMS Normalization?
計算量の違い
Layer Normalizationにおいては、
- 平均の計算
- 分散の計算
- 正規化(スケーリング)
でそれぞれ O(d) の計算量がかかるので、3d 程度の計算となります。
一方で、RMS Normalizationでは、
- 二乗和の計算
- スケーリング
でそれぞれ同じくO(d) の計算量がかかるので、2d 程度の計算となります。
この1/3程度の削減がLLMの世界だと大きいのだろうなと推測できます。
GPUのメモリ消費削減、単に計算時間の削減など・・・・
Attention
Multi Head AttentionとGrouped Query Attention
gpt-2ではMulti Head Attentionを採用して、どのTokenが他のどのTokenを強く参照しているかを表現できる様にしました。Multi Head Attentionではトークンごと(Queryごと)にKeyとValueの組を一つずつ持っていたため、計算コストが非常に大きい状態でした。
それを解決するためにgpt-ossではGrouped Query Attentionを採用しています。これはQueryヘッドの数は変えず、KVヘッドを共有する様にしたAttentionです。イメージ図は以下。

KVヘッドを共通化することで、表現力が低下しそうですがGQAを提案した論文での記載の通り、Multi Head Attentionと同等の精度を達成できていることが報告されています。
“We show that up-trained GQA achieves quality close to multi-head attention with comparable speed to MQA.”
gpt-ossだけでなく、Llama-2やMistralにもこの構造が導入されていることから、質を保ちながらパラメータ数、計算量を減らすのにいい手法であったことが伺えます。
Sliding Window Attention
長い系列を扱う際には すべてのトークン同士の関連度を計算する Full Attention では計算量・メモリ消費が急増してしまいます。
これを解決するために提案されたのが Sliding Window Attention(またはSliding Attention) です。
これは「各トークンが系列全体を見るのではなく、自分の周囲の一定範囲(スライディングウィンドウ)だけを参照する」という仕組みです。
例えばウィンドウ幅
Sliding Attention は「どのトークンを参照できるかをあえて制限する」ことで、
計算・メモリを節約しつつも文脈の局所性を捉えるのに強く、長文処理の基盤技術のひとつとなっています。
MLP
MLPにおける大きな変化は、活性化関数がGELU→SwiGLUに変わったことです。
活性化関数の比較
それぞれの式は以下の通り。

どちらも滑らかな関数で負側にも小さな勾配を持っています。
計算量としてはぱっと見はGELUの方が多そうだけど、近似式を使えるっぽいのであまり問題にならなさそう?
近似式を使わないのであれば、計算量的にSiLUが選ばれるのは納得できます。
Mixture of Expert(MoE)
MoEとは、複数の最適化されたMLP(Expert)から入力に応じて、最適な出力の組み合わせを選択する仕組み。
従来のMLPとの違い
従来のMLP
- 1つのMLPで全てのタスクを処理
- 全ての重みを常に使用
MoE
- 複数のMLPを並列配置
- 入力に応じて最適なMLPのみを選択
MoEのイメージ
すごい簡単な図ですが、やっていることは以下の様な感じ。

MoEの効果
- 従来の単一MLPでは実現できない専門性と効率性を両立可能
- 多くのExpertを持つことで、汎化性能を獲得可能
こうまとめてみると、個別最適化を並列で行うことで専門性と汎化性能を両立できるというのは納得感があります。こういうのを思いつくのはすごいなぁ(小並感)という感じです。
まとめ
本記事では、gpt-2からgpt-ossへの進化をモデル構造の観点から詳しく見てみました。LLMの発展が目覚ましい昨今でもgpt-2の構造は綺麗で洗練されていると感じました。(Transformer強い。)
gpt-2→gpt-ossの変化を見ると、思っていたより計算量削減方向のアーキテクチャ改善がありました。個人的にも、ここから先は表現力の向上よりは計算量削減、モデルの軽量化がどんどん進むと思っています。
今後はSLM(Small Language Model)の実現を進めるにあたってどの様な革新的なモデル構造の変化が起こるか楽しみです!!
Discussion