🐈‍⬛

ビットコインのHDウォレットと鍵導出の仕組み

2023/04/25に公開

Bitcoin

暗号通貨のウォレット

暗号通貨のウォレットは、現実世界のウォレットとは少し異なります。現実世界のウォレットには通貨が入っていますが、暗号通貨のウォレットには（暗号）通貨は入っていません。暗号通貨のウォレットには、送金に使用するアドレスの秘密鍵が入っています。

非決定性ウォレット

ビットコインは匿名性の観点から、送受金に使用するアドレスを毎回作り替えることを推奨しています。初期のビットコインウォレットは、送受金のたびに新しい秘密鍵を作成し、そこから新しいビットコインアドレスを作成していました。また、用途に応じてアドレスを使い分ける場合、その分の秘密鍵をウォレットに記録しておく必要がありました。つまり、10通りの用途でビットコインウォレットを運用しようとした場合、10個の秘密鍵をウォレットに記録していました。また、バックアップのために10個の秘密鍵情報を紙に記録して保管する必要がありました。

このように、管理する秘密鍵が増えるとユーザにとっては負荷が大きくなってしまいます。そこで、登場したのが決定性ウォレットです。

決定性ウォレット

決定性ウォレットは、1つの共通の「シード」から一定のルールに従って複数の秘密鍵を決定的に生成するウォレットです。決定性ウォレットでは、1つのシードさえあれば、作成した秘密鍵を復元することが可能であるため、このシードだけバックアップを取っておけば十分です。決定性ウォレットと非決定性ウォレットにおいて、バックアップが必要な情報の違いを表した図を以下に示します。

シードは乱数生成器で得られた 128bit 以上の乱数です。このシードはルートシードとも呼ばれます。ルートシードのバックアップを取るために、単に 128bit の羅列ではなく、人間にもわかりやすい英単語の列（ニーモニックコード）に変換する仕組みもあります。最近は、ニーモニックに対応したウォレットが多いと思います。ニーモニックについては BIP39^[1] にて定義されています。

秘密鍵を $k$ とすると、公開鍵 $K$ は楕円曲線上のスカラー倍算によって計以下のように作成されます（ $G$ は生成元であり固定値）。

K = kG

決定性ウォレットを実現する最も簡単な方法は、インデックス値を使用する方法です。つまり最初の秘密鍵を $k$ とすると、それ以降の鍵が $k + 1$ , $k + 2$ となり、公開鍵は $(k + 1)G$ , $(k+2)G$ となります。このような連続するインデックスを使用した場合、最初の公開鍵を $kG = Q$ とすると次の公開鍵が $(k+1)G=Q+G$ となるため、容易に推定することができてしまいます。

この問題を解決するために、256bit の乱数 $c$ とインデックスを使用した $\rm{HMAC}$ を使用する方法が考えられました。乱数 $c$ のことを チェーンコード と言います。公開鍵は以下のように計算されます（ $i$ はインデックス）。

K_i = (k+\rm{HMAC}(i,c))G

ただし、実際の計算には固定の $k$ と $c$ は使用していません。 $h_{i+1}={\rm HMAC \textrm{-} SHA512}(k_i+c_i)$ としたとき、 $k_{i+1}$ は $h_{i+1}$ の左半分 256bit、 $c_{i+1}$ は $h_{i+1}$ の右半分 256bit になります。

シードから秘密鍵とチェーンコードを作成するまでのフローチャートを以下に示します。

階層型決定性ウォレット（HD ウォレット）

HD ウォレットは BIP32^[2] と BIP44^[3] で定義されています。HD ウォレットでは、下図のように鍵を親・子・孫のように階層的に管理しています。この構造によって、各ブランチを異なる用途で使用することができます。

HD ウォレットでは、親公開鍵、親チェーンコード、インデックスを使用して、子鍵導出（CKD: Child Key Derivation）関数を通して親鍵から子鍵を生成します。Python ライブラリの bip32^[4] のソースコードをみてみましょう。子秘密鍵を生成しているメソッドの入力は、親秘密鍵、親チェーンコード、インデックスです。まず、親秘密鍵から親公開鍵を生成しています。親公開鍵と親チェーンコード、インデックスを使って ${\rm HMAC \textrm{-} SHA512}$ を取った後に、はじめの 32byte と親秘密鍵を楕円曲線上のスカラー倍算しています。子秘密鍵を生成するフローチャート図を以下に示します。

def _derive_unhardened_private_child(privkey, chaincode, index):
    pubkey = _privkey_to_pubkey(privkey)
    payload = hmac.new(
        chaincode, pubkey + index.to_bytes(4, "big"), hashlib.sha512
    ).digest()
    try:
        child_private = coincurve.PrivateKey(payload[:32]).add(privkey)
    except ValueError:
        raise BIP32DerivationError(
            "Invalid private key at index {}, try the " "next one!".format(index)
        )
    return child_private.secret, payload[32:]

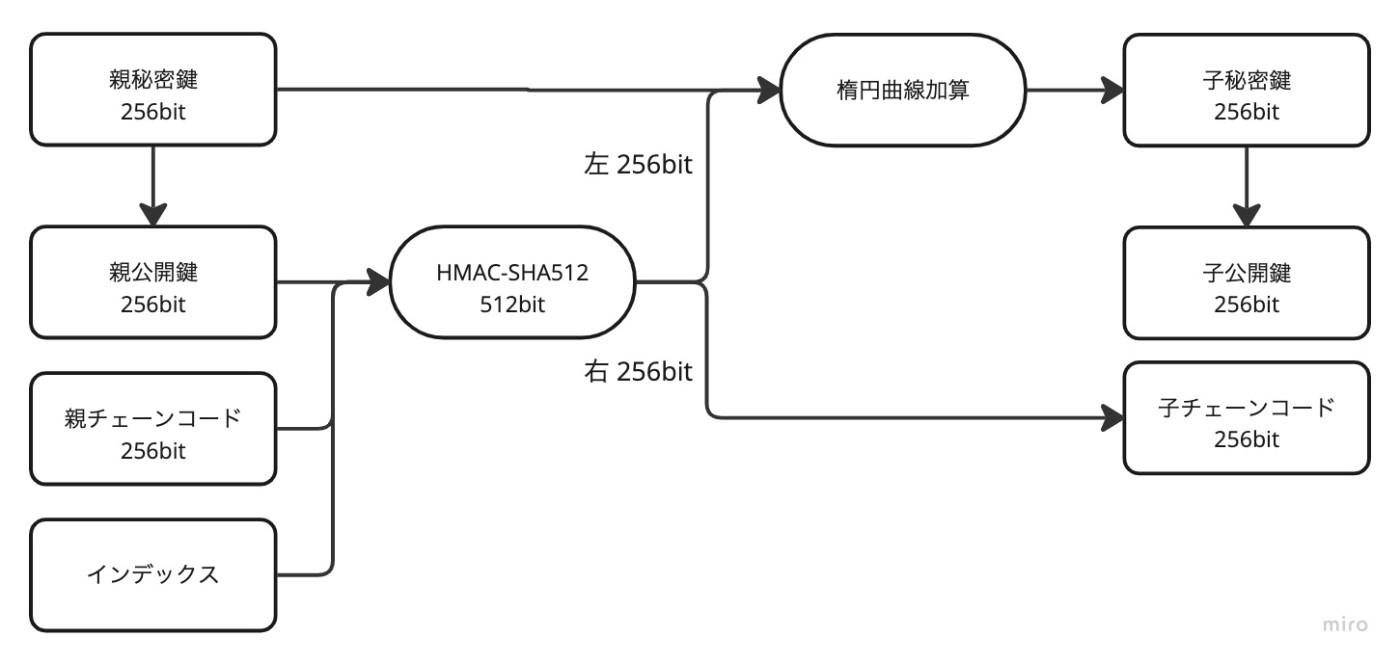
子鍵導出関数の特徴として、もし、ある子秘密鍵を持っていたとしても、親チェーンコードを持っていなければ他の子（いわゆる兄弟）秘密鍵を計算することはできません。また、子秘密鍵を知っていたとしても、子チェーンコードを知っていなければ孫秘密鍵を計算することはできません。

親秘密鍵を $k_i$ 、楕円曲線のベースポイントを $G$ 、親公開鍵を $K_i$ とします。親公開鍵の導出を式で表すと以下のようになります。

K_1 = k_1 \times G\\

また、拡張秘密鍵による子秘密鍵の導出を式で表すと以下のようになります。

k_2 = k_1 + {\rm HMAC \textrm{-} SHA512}(K_1, c_1, i)[:32]

子秘密鍵から子公開鍵の導出は親の時と同様です。

K_2 = k_2 \times G

鍵とチェーンコードを連結したものを拡張鍵と言います。拡張鍵には「拡張秘密鍵」と「拡張公開鍵」の2つがあります。拡張秘密鍵は、秘密鍵とチェーンコードの組み合わせであり、子秘密鍵を生成することに使用されます（その後に子公開鍵も計算できます）。拡張秘密鍵から子秘密鍵が計算できることは、上の図を参照すれば明らかです。

拡張公開鍵は、公開鍵とチェーンコードの組み合わせであり、子公開鍵を生成することができます（子秘密鍵は生成することができません）。拡張公開鍵は以下のように子公開鍵を生成します。

K_2 = K_1 + {\rm HMAC \textrm{-} SHA512}(K_1, c_1, i)[:32] \times G

秘密鍵を必要とせずに公開鍵を直接生成しているので違和感があるかもしれません。公開鍵は秘密鍵に $G$ をかけることで生成していることを思い出してください。拡張秘密鍵で子秘密鍵を生成する式の両辺に $G$ をかけると、上の式の形になることがわかります。

k_2 \times G = (k_1 + {\rm HMAC \textrm{-} SHA512}(K_1, c_1, i)[:32]) \times G

強化子公開鍵

拡張公開鍵は、秘密鍵を必要とせずに子公開鍵を導出できる点においてとても有用です。しかし、拡張公開鍵はチェーンコードを含んでいるため、もし子秘密鍵が漏洩した場合、親秘密鍵を推測できてしまいます。その結果、すべての他の子秘密鍵を導出できてしまいます。

k_2 = k_1 + {\rm HMAC \textrm{-} SHA512}(K_1, c_1, i)[:32]\\ k_2 - {\rm HMAC \textrm{-} SHA512}(K_1, c_1, i)[:32] = k_1

このリスクを避けるために、強化導出（Hardened Derivation） というものがあります。これは親公開鍵の代わりに親秘密鍵を使って、子チェーンコードを作成することによって親公開鍵と子チェーンコードの関係を絶っています。

強化導出によって生成された公開鍵を強化公開鍵と言います。もし、親公開鍵と親チェーンコードを知る第三者に子秘密鍵が漏洩したとしても、親秘密鍵を導くことはできません。

参考文献

脚注