ガウスの求積法とは
概要
ガウスの求積法とは積分値を評価する方法の1つである。次のように何らかの関数f(x)を区間[a,b]の間で積分したい場合を考える。
\begin{equation}
S = \int_{a}^{b} f(x) dx
\end{equation}
この積分を以下のように近似するのがガウスの求積法である。
\begin{equation}
\int_{a}^{b} f(x) dx \simeq \sum_{i=1}^n c_i f(x_i)
\end{equation}
これは任意の積分が特定の点\{x_i\}におけるf(x)の値にそれぞれ重み\{c_i\}をかけて足し合わせたもので近似できることを意味している。nは必要とされる精度に合わせて設定する。
ガウスの求積法の性質
性質1
f(x)が2n-1次以下の多項式であるとき、式(2)の両辺は厳密に等しくなる。
性質2
ガウスの求積法はその計算に直交多項式の性質を用いている。用いる直交多項式は後述するように求めたい積分の区間により選ぶ。
式(2)の\{x_i\}(以下分点と呼ぶ。)は用いる直交多項式のn次の零点である。つまり用いる直交多項式を\{p_i (x)\} (i=0,1,...)とするとき、分点は
\begin{equation}
p_n (x) = 0
\end{equation}
の解として与えられる。
性質3
重み\{c_i\}は以下の式で計算される。
\begin{equation}
c_i \equiv \int_{a}^{b} L_i (x) dx
\end{equation}
ここで、
\begin{equation}
\begin{align*}
L_i(x) &= \frac{ (x - x_0) (x - x_1) \cdots (x - x_{i-1}) (x - x_{i+1}) \cdots (x - x_{n-1}) }{ (x_i - x_0) (x_i - x_1) \cdots (x_i - x_{i-1}) (x_i - x_{i+1}) \cdots (x_i - x_{n-1})} \\
&= \underset{j \neq i}{ \underset{ j=0 }{ \overset{n-1}{\Pi} } } \frac{x - x_j }{ x_i - x_j }
\end{align*}
\end{equation}
である。
使用時の注意
ガウスの求積法は直交多項式を用いており、積分区間に応じて用いる直交多項式が異なる。有限の場合は適当な変数変換を行って、積分区間が利用する直交多項式の区間[-1,1]になるようにする。
| 積分区間 |
用いる直交多項式 |
| 有限 [a,b] |
ルジャンドル多項式、シェビチェフ多項式 |
| 無限 [-\infty, \infty]
|
エルミート多項式 |
| 半無限 [0, \infty]
|
ラゲール多項式 |
証明
積分区間が有限[a,b]のときにルジャンドル多項式を用いる場合を例にとって式(2)および性質1~3を証明する。これはガウス―ルジャンドルの積分公式と呼ばれる。
積分区間が同じく有限でシェビチェフ多項式を用いる場合や、積分区間が無限、半無限の場合も用いる直交多項式が異なるだけで同じ説明が成り立つ。
以下の積分を評価したいものとする。
\begin{equation}
S = \int_{a}^{b} f(x) dx
\end{equation}
変数変換
\begin{equation}
x = \frac{a+b}{2} + \frac{(b-a)t}{2}
\end{equation}
を行うと、
\begin{equation}
\begin{align*}
S &= \int_{-1}^1 f \left( \frac{a+b}{2} + \frac{(b-a)t}{2} \right) \cdot \frac{2}{b-a} dt \\
&= \int_{-1}^1 \hat{f} (t) dt
\end{align*}
\end{equation}
と書ける。ここで、
\begin{equation}
\hat{f} (t) \equiv f \left( \frac{a+b}{2} + \frac{(b-a)t}{2} \right) \cdot \frac{2}{b-a} dt
\end{equation}
とおいた。
式(8)の被積分関数\hat{f}(t)が2n-1次の多項式を使って表せると仮定する。
\hat{f}(t)をn次の直交多項式P_n (t)で割った結果得られた関数をQ(t)、割った余りの関数をR(t)とすると以下のように書ける。
\begin{equation}
\hat{f}(t) = P_n (t) Q(t) + R(t)
\end{equation}
ここでR(t)は(n-1)次以下の多項式である。
これを(8)に代入すると、
\begin{equation}
\begin{align*}
S &= \int_{-1}^1 \left( P_n (t) Q(t) + R(t) \right) dt \\
&= \int_{-1}^1 P_n (t) Q(t) dt + \int_{-1}^1 R(t) dt
\end{align*}
\end{equation}
と書ける。
ここで、式(11)の積分値を通常の数値積分と同様に関数の横軸を適当に区切り求める(図1)。但しこの区切り(分点)を等間隔ではなく、上で用いた直交多項式\{P_i(t)\}のn次の零点(P_n(t) = 0の解)を用いる。
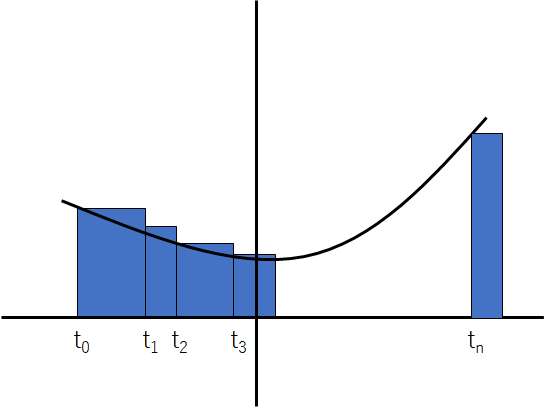
図1. 積分のイメージ
このとき、式(11)の右辺第1項は、
\begin{equation}
\begin{align*}
\int_{-1}^1 P_n (t) Q(t) dt &\simeq \sum_{i=1}^n c_i P_n(t_i) Q(t_i) \\
&= 0 \ \ \ \left( \because P_n(t_i) = 0 \right)
\end{align*}
\end{equation}
となる。ここで\{ t_i \}は直交多項式\{P_i(t)\}のn次の分点、c_iは重み係数である。
よって、積分値を直交多項式の零点\{ t_i \}での関数値を使った和として評価するならば、
\begin{equation}
\begin{align*}
S = \int_{-1}^1 f(t) dt \simeq \int_{-1}^1 R(t) dt
\end{align*}
\end{equation}
が成り立つ。
ところで、P_n(t_i)=0より式(10)からR(t_i) = f(t_i)である。つまりn個の点\{ t_i \}においてR(t)とf(t)は一致する。
n個の点を通る多項式はn-1次のラグランジュ補間多項式で正確に表せることが知られている 。これを用いると、
\begin{equation}
\begin{align*}
R(t) = \sum_{i=1}^n R(t_i) L_i (t) = \sum_{i=1}^n f(t_i) L_i (t)
\end{align*}
\end{equation}
と書ける。ここで、
\begin{equation}
\begin{align*}
L_i(t) &= \frac{ (t - t_0) (t - t_1) \cdots (t - t_{i-1}) (t - t_{i+1}) \cdots (t - t_{n-1}) }{ (t_i - t_0) (t_i - t_1) \cdots (t_i - t_{i-1}) (t_i - t_{i+1}) \cdots (t_i - t_{n-1})} \\
&= \underset{j \neq i}{ \underset{ j=0 }{ \overset{n-1}{\Pi} } } \frac{t - t_j }{ t_i - t_j }
\end{align*}
\end{equation}
である。よって、式(13)の積分は
\begin{equation}
\begin{align*}
S &= \int_{-1}^1 f(t) dt \\
&\simeq \int_{-1}^1 R(t) dt \\
&= \int_{-1}^1 \sum_{i=1}^n R(t_i) L_i (t) dt \\
&= \int_{-1}^1 \sum_{i=1}^n f(t_i) L_i (t) dt \ \ \ \ \left( \ \because R(t_i)=f(t_i) \ \right) \\
&= \sum_{i=1}^n f(t_i) \int_{-1}^1 L_i (t) dt
\end{align*}
\end{equation}
と書ける。ここで、
\begin{equation}
\begin{align*}
c_i \equiv \int_{-1}^1 L_i (t) dt
\end{align*}
\end{equation}
とおくと、式(16)は
\begin{equation}
\begin{align*}
S = \int_{-1}^1 f(t) dt \simeq \sum_{i=1}^n c_i f(t_i)
\end{align*}
\end{equation}
と書ける。これがガウス-ルジャンドルの積分公式である。
重み\{c_i\}は分点\{t_i\}から式(15)、(17)を用いて事前に求めることができる。
つまり被積分関数f(x)の形によらず事前に計算している値を用いればよい。
更には、重み\{c_i\}と分点\{t_i\}の数表は例えば"Abramowitz and Stegun"などに記載されているため、それを用いればよい。



Discussion