Zenn
💡

ニューラルネットワークを数式から理解する

2022/08/17に公開
機械学習
nn
backpropagation
tech

はじめに

タイトルのとおり、ニューラルネットワーク(NN)を勉学するにあたり、その内部でどのような計算が行われているか詳しく確認したかったため、理解した過程を本稿に残します。

前提

  • サンプルデータはIrisのデータセット
    (4つの特徴量で、花の品種を3分類予測)
  • 活性化関数は、Sigmoid関数を用いる
  • 損失関数は、平均二乗誤差とする
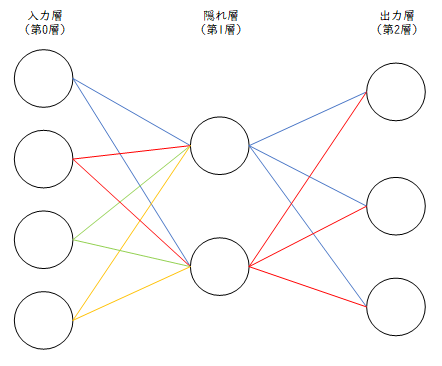
  • 入力層: 4ノード、隠れ層: 2ノード、出力層: 3ノード
  • バイアスも考慮

計算の流れ

  1. ハイパーパラメータ初期設定
  2. 重みの初期化
  3. 順伝播 - 隠れ層における線形和関数計算
  4. 順伝播 - 隠れ層における活性化関数計算
  5. 順伝播 - 出力層における線形和関数計算
  6. 順伝播 - 出力層における活性化関数計算
  7. 出力層の損失
  8. 逆伝播 - 出力層における偏微分計算 (共通部分)
  9. 逆伝播 - 出力層における損失関数の入力による偏微分計算
  10. 逆伝播 - 出力層における損失関数の重みによる偏微分計算
  11. 逆伝播 - 出力層における損失関数のバイアスによる偏微分計算
  12. 逆伝播 - 隠れ層における偏微分計算 (共通部分)
  13. 逆伝播 - 隠れ層における損失関数の重みによる偏微分計算
  14. 逆伝播 - 隠れ層における損失関数のバイアスによる偏微分計算
  15. 最適化

逆伝播の計算概要

逆伝播では、損失(出力)に対する重みの偏微分、バイアスの偏微分を算出し、算出値を元に重みとバイアスを最適化する。
また、損失に対する入力の偏微分を算出し、前層の逆伝播(偏微分)に繋げる。

\begin{align} \frac{\partial{L}}{\partial{w}} &= \frac{\partial{L}}{\partial{a}} \times \frac{\partial{a}}{\partial{y}} \times \frac{\partial{y}}{\partial{w}} \\ \frac{\partial{L}}{\partial{b}} &= \frac{\partial{L}}{\partial{a}} \times \frac{\partial{a}}{\partial{y}} \times \frac{\partial{y}}{\partial{b}} \\ \frac{\partial{L}}{\partial{x}} &= \frac{\partial{L}}{\partial{a}} \times \frac{\partial{a}}{\partial{y}} \times \frac{\partial{y}}{\partial{x}} \end{align} \\ \begin{bmatrix} L & : & \text{損失関数} \\ a & : & \text{活性化関数} \\ y & : & \text{線形和関数} \\ w & : & \text{重み} \\ b & : & \text{バイアス} \\ x & : & \text{入力} \end{bmatrix}

なお、損失関数は次のとおり定義する。

Loss=\frac{(A-Truth)^2}{2}

ここで A は活性化関数 a の出力と等しく、Truth は真値とする。
また、(1)～(3)の勾配関数は次のように解釈でき、

  • \frac{\partial{L}}{\partial{w}} は各層の出力に対する重みの傾き
  • \frac{\partial{L}}{\partial{b}} は各層の出力に対するバイアスの傾き
  • \frac{\partial{L}}{\partial{x}} は各層の出力に対する入力の傾き

関数の勾配に着目して微少にパラメータを変化させて最適な値に近づける。
重みとバイアスの最適化は、次のように勾配と異符号の向きにパラメータを調整することで実現する。

\begin{align*} w &\leftarrow w-\eta\frac{\partial{L}}{\partial{w}} \\\\ b &\leftarrow b-\eta\frac{\partial{L}}{\partial{b}} \end{align*}

ここで \eta \ (0<\eta<1) を学習率という。

上記(1)～(3)の勾配関数は、 \frac{\partial{L}}{\partial{a}} \times \frac{\partial{a}}{\partial{y}} を共通に持つことから、まずは \frac{\partial{L}}{\partial{y}} = \frac{\partial{L}}{\partial{a}} \times \frac{\partial{a}}{\partial{y}} を求める。

\begin{align*} \frac{\partial{L}}{\partial{a}} &= \left(\frac{(A - Truth)^2}{2}\right)' \\ &= (A - Truth) \cdot (A - Truth)' \\ &= (A - Truth) \cdot 1 \\ &= (A - Truth) \\ \\ \frac{\partial{a}}{\partial{y}} &= sigmoid(y)' \\ &= \{sigmoid(y) \times (1 - sigmoid(y)) \} \\ \\ & \text{ 合成関数の連鎖律から } \\ \frac{\partial{L}}{\partial{y}} &= \frac{\partial{L}}{\partial{a}} \times \frac{\partial{a}}{\partial{y}} \\ &= (A - Truth) \times \{sigmoid(y) \times (1 - sigmoid(y)) \} \\ & \text{ また、 A は活性化関数 a の出力と等しいことから } \\ \frac{\partial{L}}{\partial{y}} &= (sigmoid(y) - Truth) \cdot \{sigmoid(y) \times (1 - sigmoid(y)) \} \\ \end{align*}

または、

\begin{align*} \frac{\partial{L}}{\partial{y}} &= (\frac{(sigmoid(y)-Truth)^2}{2})' \\ &= (sigmoid(y) - Truth) \cdot (sigmoid(y) - Truth)' \\ &= (sigmoid(y) - Truth) \cdot sigmoid(y)' \\ &= (sigmoid(y) - Truth) \cdot \{sigmoid(y) \times (1 - sigmoid(y)\} \end{align*}

計算過程

計算過程と共にPython でコーディングを行い理解を深めてみよう。

事前準備

ライブラリをインポート

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

データセット読込

data = load_iris()
X = data.data
y = data.target

データセットを訓練データと試験データに分割

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20)

関数定義

def sigmoid(x):  # 活性化関数 (シグモイド関数とする)
    return 1 / (1 + np.exp(-x))

def mean_squared_error(y_pred, y_true):  # 評価関数
    return ((y_pred - y_true)**2).sum() / (2*y_pred.size)

def accuracy(y_pred, y_true):  # 正解率関数
    acc = y_pred.argmax(axis=1) == y_true.argmax(axis=1)
    return acc.mean()
\frac{sigmoid(x)}{\partial{x}} = sigmoid(x) \times (1-sigmoid(x))

1. ハイパーパラメータ初期設定

# ハイパーパラメータ
learning_rate = 0.1  # 学習率
iterations = 5000  # 学習回数
N = y_train.size  # バッチ数
input_size = 4  # 入力ノード数
hidden_size = 2  # 隠れノード数
output_size = 3  # 出力ノード数
# 計算過程格納用に変数作成
results = pd.DataFrame(columns=['mse', 'accuracy'])

2. 重みの初期化

np.random.seed(10)  # 乱数シードを固定
# 隠れ層パラメータ
W1 = np.random.normal(scale=0.5, size=(input_size, hidden_size))  # 重み
B1 = np.random.normal(scale=0.5, size=hidden_size)  # バイアス
# 出力層パラメータ
W2 = np.random.normal(scale=0.5, size=(hidden_size, output_size))  # 重み
B2 = np.random.normal(scale=0.5, size=output_size)  # バイアス

隠れ層重み

\begin{align*} W1 &\leftarrow \begin{pmatrix} w_{11}^1 & w_{12}^1 & w_{13}^1 & w_{14}^1 \\ w_{21}^1 & w_{22}^1 & w_{23}^1 & w_{24}^1 \end{pmatrix}^\top = \begin{pmatrix} w_{11}^1 & w_{21}^1 \\ w_{12}^1 & w_{22}^1 \\ w_{13}^1 & w_{23}^1 \\ w_{14}^1 & w_{24}^1 \end{pmatrix} \\ B1 &\leftarrow \begin{pmatrix}b_1^1 & b_2^1\end{pmatrix} \end{align*}

出力層重み

\begin{align*} W2 &\leftarrow \begin{pmatrix} w_{11}^2 & w_{12}^2 \\ w_{21}^2 & w_{22}^2 \\ w_{31}^2 & w_{32}^2 \\ \end{pmatrix}^\top = \begin{pmatrix} w_{11}^2 & w_{21}^2 & w_{31}^2 \\ w_{12}^2 & w_{22}^2 & w_{32}^2 \\ \end{pmatrix} \\\\ B2 &\leftarrow \begin{pmatrix}b_1^2 & b_2^2 & b_3^2\end{pmatrix} \end{align*}

3. 順伝播 - 隠れ層における線形和関数計算

Z1 = np.dot(X_train, W1) + B1

入力

\begin{align*} X\_train &= \begin{pmatrix} x_{11} & x_{12} & x_{13} & x_{14} \\ x_{21} & x_{22} & x_{23} & x_{24} \\ x_{31} & x_{32} & x_{33} & x_{34} \\ x_{41} & x_{42} & x_{43} & x_{44} \\ \vdots & \vdots & \vdots & \vdots \\ \end{pmatrix} \end{align*}

線形和

\begin{align*} Z1 &\leftarrow X\_train \cdot W1 + B1 \\\\ &= \begin{pmatrix} x_{11} & x_{12} & x_{13} & x_{14} \\ x_{21} & x_{22} & x_{23} & x_{24} \\ x_{31} & x_{32} & x_{33} & x_{34} \\ x_{41} & x_{42} & x_{43} & x_{44} \\ \vdots & \vdots & \vdots & \vdots \\ \end{pmatrix} \cdot \begin{pmatrix} w_{11}^1 & w_{21}^1 \\ w_{12}^1 & w_{22}^1 \\ w_{13}^1 & w_{23}^1 \\ w_{14}^1 & w_{24}^1 \\ \end{pmatrix} + \begin{pmatrix}b_1^1 & b_2^1\end{pmatrix} \\ &= \scriptsize{ \begin{pmatrix} x_{11} \cdot w_{11}^1 + x_{12} \cdot w_{12}^1 + x_{13} \cdot w_{13}^1 + x_{14} \cdot w_{14}^1 + b_1^1 & x_{11} \cdot w_{21}^1 + x_{12} \cdot w_{22}^1 + x_{13} \cdot w_{23}^1 + x_{14} \cdot w_{24}^1 + b_2^1 \\ x_{21} \cdot w_{11}^1 + x_{22} \cdot w_{12}^1 + x_{23} \cdot w_{13}^1 + x_{24} \cdot w_{14}^1 + b_1^1 & x_{21} \cdot w_{21}^1 + x_{22} \cdot w_{22}^1 + x_{23} \cdot w_{23}^1 + x_{24} \cdot w_{24}^1 + b_2^1 \\ x_{31} \cdot w_{11}^1 + x_{32} \cdot w_{12}^1 + x_{33} \cdot w_{13}^1 + x_{34} \cdot w_{14}^1 + b_1^1 & x_{31} \cdot w_{21}^1 + x_{32} \cdot w_{22}^1 + x_{33} \cdot w_{23}^1 + x_{34} \cdot w_{24}^1 + b_2^1 \\ x_{41} \cdot w_{11}^1 + x_{42} \cdot w_{12}^1 + x_{43} \cdot w_{13}^1 + x_{44} \cdot w_{14}^1 + b_1^1 & x_{41} \cdot w_{21}^1 + x_{42} \cdot w_{22}^1 + x_{43} \cdot w_{23}^1 + x_{44} \cdot w_{24}^1 + b_2^1 \\ \vdots & \vdots \\ \end{pmatrix} } \\ &= \begin{pmatrix} y_{11}^1 & y_{12}^1 \\ y_{21}^1 & y_{22}^1 \\ y_{31}^1 & y_{32}^1 \\ y_{41}^1 & y_{42}^1 \\ \vdots & \vdots \\ \end{pmatrix} \\ \end{align*}

4. 順伝播 - 隠れ層における活性化関数計算

A1 = sigmoid(Z1)

シグモイド関数により隠れ層の出力を得る

\begin{align*} A1 &\leftarrow \frac{1}{1+e^{-Z1}} \\\\ &= \begin{pmatrix} a_{11}^1 & a_{12}^1 \\ a_{21}^1 & a_{22}^1 \\ a_{31}^1 & a_{32}^1 \\ a_{41}^1 & a_{42}^1 \\ \vdots & \vdots \end{pmatrix} \end{align*}

5. 順伝播 - 出力層における線形和関数計算

Z2 = np.dot(A1, W2) + B2

入力

A1= \begin{pmatrix} a_{11}^1 & a_{12}^1 \\ a_{21}^1 & a_{22}^1 \\ a_{31}^1 & a_{32}^1 \\ a_{41}^1 & a_{42}^1 \\ \vdots & \vdots \end{pmatrix}

線形和

\begin{align*} Z2 &\leftarrow A1 \cdot W2 + B2 \\\\ &= \begin{pmatrix} a_{11}^1 & a_{12}^1 \\ a_{21}^1 & a_{22}^1 \\ a_{31}^1 & a_{32}^1 \\ a_{41}^1 & a_{42}^1 \\ \vdots & \vdots \end{pmatrix} \cdot \begin{pmatrix} w_{11}^2 & w_{21}^2 & w_{31}^2 \\ w_{12}^2 & w_{22}^2 & w_{32}^2 \\ \end{pmatrix} + \begin{pmatrix}b_1^2 & b_2^2 & b_3^2\end{pmatrix} \\ &= \scriptsize{\begin{pmatrix} a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + 1 \cdot b_{1}^2 & a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + 1 \cdot b_{2}^2 & a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + 1 \cdot b_{3}^2 \\ a_{21}^1 \cdot w_{11}^2 + a_{22}^1 \cdot w_{12}^2 + 1 \cdot b_{1}^2 & a_{21}^1 \cdot w_{21}^2 + a_{22}^1 \cdot w_{22}^2 + 1 \cdot b_{2}^2 & a_{21}^1 \cdot w_{31}^2 + a_{22}^1 \cdot w_{32}^2 + 1 \cdot b_{3}^2 \\ a_{31}^1 \cdot w_{11}^2 + a_{32}^1 \cdot w_{12}^2 + 1 \cdot b_{1}^2 & a_{31}^1 \cdot w_{21}^2 + a_{32}^1 \cdot w_{22}^2 + 1 \cdot b_{2}^2 & a_{31}^1 \cdot w_{31}^2 + a_{32}^1 \cdot w_{32}^2 + 1 \cdot b_{3}^2 \\ a_{41}^1 \cdot w_{11}^2 + a_{42}^1 \cdot w_{12}^2 + 1 \cdot b_{1}^2 & a_{41}^1 \cdot w_{21}^2 + a_{42}^1 \cdot w_{22}^2 + 1 \cdot b_{2}^2 & a_{41}^1 \cdot w_{31}^2 + a_{42}^1 \cdot w_{32}^2 + 1 \cdot b_{3}^2 \\ \vdots & \vdots & \vdots \end{pmatrix}} \\ &= \begin{pmatrix} y_{11}^2 & y_{12}^2 & y_{13}^2 \\ y_{21}^2 & y_{22}^2 & y_{23}^2 \\ y_{31}^2 & y_{32}^2 & y_{33}^2 \\ y_{41}^2 & y_{42}^2 & y_{43}^2 \\ \vdots & \vdots & \vdots \end{pmatrix} \end{align*}

6. 順伝播 - 出力層における活性化関数計算

A2 = sigmoid(Z2)

シグモイド関数により出力層の出力を得る。推論=A2となる。

\begin{align*} A2 &\leftarrow \frac{1}{1+e^{-Z2}} \\ &= \begin{pmatrix} a_{11}^2 & a_{12}^2 & a_{13}^2 \\ a_{21}^2 & a_{22}^2 & a_{23}^2 \\ a_{31}^2 & a_{32}^2 & a_{33}^2 \\ a_{41}^2 & a_{42}^2 & a_{43}^2 \\ \vdots & \vdots & \vdots \end{pmatrix} &\Rightarrow 推論値 \end{align*}

7. 出力層の損失

E2 = A2 - np.identity(output_size)[y_train]

計算過程として、推論値 - 真値を算出する。

\begin{align*} E2 &\leftarrow (Prediction - Truth) \\ &= A2 - Truth \\\\ &= \begin{pmatrix} a_{11}^2 & a_{12}^2 & a_{13}^2 \\ a_{21}^2 & a_{22}^2 & a_{23}^2 \\ a_{31}^2 & a_{32}^2 & a_{33}^2 \\ a_{41}^2 & a_{42}^2 & a_{43}^2 \\ \vdots & \vdots & \vdots \end{pmatrix} - \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \vdots & \vdots & \vdots \end{pmatrix} \\ &= \begin{pmatrix} a_{11}^2 - 1 & a_{12}^2 - 0 & a_{13}^2 - 0 \\ a_{21}^2 - 0 & a_{22}^2 - 0 & a_{23}^2 - 1 \\ a_{31}^2 - 0 & a_{32}^2 - 1 & a_{33}^2 - 0 \\ a_{41}^2 - 1 & a_{42}^2 - 0 & a_{43}^2 - 0 \\ \vdots & \vdots & \vdots \end{pmatrix} \end{align*}

8. 逆伝播 - 出力層における偏微分計算 (共通部分)

dE2 = E2 * A2 * (1 - A2)

上記、逆伝播の計算概要で示した勾配関数の共通部分を算出する。

\begin{align*} \frac{\partial{L}}{\partial{y}} &= (sigmoid(y) - Truth) \cdot \{sigmoid(y) \times (1 - sigmoid(y)) \} \\ &= (A2 - Truth) \times A2 \times (1-A2) \\ &= E2 \times A2 \times (1-A2) \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \frac{\partial{L_2}}{\partial{y_{21}^2}} & \frac{\partial{L_2}}{\partial{y_{22}^2}} & \frac{\partial{L_2}}{\partial{y_{23}^2}} \\ \frac{\partial{L_3}}{\partial{y_{31}^2}} & \frac{\partial{L_3}}{\partial{y_{32}^2}} & \frac{\partial{L_3}}{\partial{y_{33}^2}} \\ \frac{\partial{L_4}}{\partial{y_{41}^2}} & \frac{\partial{L_4}}{\partial{y_{42}^2}} & \frac{\partial{L_4}}{\partial{y_{43}^2}} \\ \vdots & \vdots & \vdots \end{pmatrix} \\ &\Rightarrow dE2 \end{align*}

9. 逆伝播 - 出力層における損失関数の入力による偏微分計算

E1 = np.dot(dE2, W2.T)

損失関数 L の入力 A1 に対する偏微分を算出する。

\begin{align*} \frac{\partial{L}}{\partial{A1}} &= \frac{\partial{L_i}}{\partial{a_{ij}^1}} = \begin{pmatrix} \frac{\partial{L_1}}{\partial{a_{11}^1}} & \frac{\partial{L_1}}{\partial{a_{12}}^1} \\ \frac{\partial{L_2}}{\partial{a_{21}^1}} & \frac{\partial{L_2}}{\partial{a_{22}}^1} \\ \vdots & \vdots \end{pmatrix} \\ &= \frac{\partial{L_i}}{\partial{f(a_{i1}^1,a_{i2}^1)}} \cdot \frac{\partial{f(a_{i1}^1,a_{i2}^1)}}{\partial{a_{ij}^1}} = \frac{\partial{L_i}}{\partial{Y_i}} \cdot \frac{\partial{Y_i}}{\partial{a_{ij}^1}} = \begin{pmatrix} \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{a_{11}^1}} & \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{a_{12}^1}} \\ \frac{\partial{L_2}}{\partial{Y_{2}}} \cdot \frac{\partial{Y_{2}}}{\partial{a_{21}^1}} & \frac{\partial{L_2}}{\partial{Y_{2}}} \cdot \frac{\partial{Y_{2}}}{\partial{a_{22}^1}} \\ \frac{\partial{L_3}}{\partial{Y_{3}}} \cdot \frac{\partial{Y_{3}}}{\partial{a_{31}^1}} & \frac{\partial{L_3}}{\partial{Y_{3}}} \cdot \frac{\partial{Y_{3}}}{\partial{a_{32}^1}} \\ \frac{\partial{L_4}}{\partial{Y_{4}}} \cdot \frac{\partial{Y_{4}}}{\partial{a_{41}^1}} & \frac{\partial{L_4}}{\partial{Y_{4}}} \cdot \frac{\partial{Y_{4}}}{\partial{a_{42}^1}} \\ \vdots & \vdots \end{pmatrix} \\ \end{align*}

ここで、ジャコビアンの連鎖律および

\begin{bmatrix} y_{11}^2 &= a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2 \\ y_{12}^2 &= a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2 \\ y_{13}^2 &= a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2 \\ \end{bmatrix}

であることから、

\begin{align*} \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{a_{11}^1}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{a_{11}^1}} \\ \frac{\partial{y_{12}^2}}{\partial{a_{11}^1}} \\ \frac{\partial{y_{13}^2}}{\partial{a_{11}^1}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{a_{11}^1}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{a_{11}^1}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{a_{11}^1}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{a_{11}^1}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{a_{11}^1}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{a_{11}^1}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot w_{11}^2 + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot w_{21}^2 + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot w_{31}^2 \\ \end{pmatrix} \\ \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{a_{12}^1}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{a_{12}^1}} \\ \frac{\partial{y_{12}^2}}{\partial{a_{12}^1}} \\ \frac{\partial{y_{13}^2}}{\partial{a_{12}^1}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{a_{12}^1}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{a_{12}^1}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{a_{12}^1}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{a_{12}^1}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{a_{12}^1}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{a_{12}^1}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot w_{12}^2 + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot w_{22}^2 + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot w_{32}^2 \\ \end{pmatrix} \\ \frac{\partial{L_2}}{\partial{Y_{2}}} \cdot \frac{\partial{Y_{2}}}{\partial{a_{21}^1}} &= \begin{pmatrix} \frac{\partial{L_2}}{\partial{y_{21}^2}} & \frac{\partial{L_2}}{\partial{y_{22}^2}} & \frac{\partial{L_2}}{\partial{y_{23}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{21}^2}}{\partial{a_{21}^1}} \\ \frac{\partial{y_{22}^2}}{\partial{a_{21}^1}} \\ \frac{\partial{y_{23}^2}}{\partial{a_{21}^1}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_2}}{\partial{y_{21}^2}} \cdot \frac{\partial{y_{21}^2}}{\partial{a_{21}^1}} + \frac{\partial{L_2}}{\partial{y_{22}^2}} \cdot \frac{\partial{y_{22}^2}}{\partial{a_{21}^1}} + \frac{\partial{L_2}}{\partial{y_{23}^2}} \cdot \frac{\partial{y_{23}^2}}{\partial{a_{21}^1}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_2}}{\partial{y_{21}^2}} \cdot \frac{\partial{}}{\partial{a_{21}^1}}(a_{21}^1 \cdot w_{11}^2 + a_{22}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_2}}{\partial{y_{22}^2}} \cdot \frac{\partial{}}{\partial{a_{21}^1}}(a_{21}^1 \cdot w_{21}^2 + a_{22}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_2}}{\partial{y_{23}^2}} \cdot \frac{\partial{}}{\partial{a_{21}^1}}(a_{21}^1 \cdot w_{31}^2 + a_{22}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_2}}{\partial{y_{21}^2}} \cdot w_{11}^2 + \frac{\partial{L_2}}{\partial{y_{22}^2}} \cdot w_{21}^2 + \frac{\partial{L_2}}{\partial{y_{23}^2}} \cdot w_{31}^2 \\ \end{pmatrix} \\ \frac{\partial{L_2}}{\partial{Y_{2}}} \cdot \frac{\partial{Y_{2}}}{\partial{a_{22}^1}} &= \dots \end{align*}

これを代入すると、

\begin{align*} \frac{\partial{L}}{\partial{A^1}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{a_{11}^1}} & \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{a_{12}^1}} \\ \frac{\partial{L_2}}{\partial{Y_{2}}} \cdot \frac{\partial{Y_{2}}}{\partial{a_{21}^1}} & \frac{\partial{L_2}}{\partial{Y_{2}}} \cdot \frac{\partial{Y_{2}}}{\partial{a_{22}^1}} \\ \frac{\partial{L_3}}{\partial{Y_{3}}} \cdot \frac{\partial{Y_{3}}}{\partial{a_{31}^1}} & \frac{\partial{L_3}}{\partial{Y_{3}}} \cdot \frac{\partial{Y_{3}}}{\partial{a_{32}^1}} \\ \frac{\partial{L_4}}{\partial{Y_{4}}} \cdot \frac{\partial{Y_{4}}}{\partial{a_{41}^1}} & \frac{\partial{L_4}}{\partial{Y_{4}}} \cdot \frac{\partial{Y_{4}}}{\partial{a_{42}^1}} \\ \vdots & \vdots \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot w_{11}^2 + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot w_{21}^2 + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot w_{31}^2 & \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot w_{12}^2 + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot w_{22}^2 + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot w_{32}^2 \\ \frac{\partial{L_2}}{\partial{y_{21}^2}} \cdot w_{11}^2 + \frac{\partial{L_2}}{\partial{y_{22}^2}} \cdot w_{21}^2 + \frac{\partial{L_2}}{\partial{y_{23}^2}} \cdot w_{31}^2 & \frac{\partial{L_2}}{\partial{y_{21}^2}} \cdot w_{12}^2 + \frac{\partial{L_2}}{\partial{y_{22}^2}} \cdot w_{22}^2 + \frac{\partial{L_2}}{\partial{y_{23}^2}} \cdot w_{32}^2 \\ \frac{\partial{L_3}}{\partial{y_{31}^2}} \cdot w_{11}^2 + \frac{\partial{L_3}}{\partial{y_{32}^2}} \cdot w_{21}^2 + \frac{\partial{L_3}}{\partial{y_{33}^2}} \cdot w_{31}^2 & \frac{\partial{L_3}}{\partial{y_{31}^2}} \cdot w_{12}^2 + \frac{\partial{L_3}}{\partial{y_{32}^2}} \cdot w_{22}^2 + \frac{\partial{L_3}}{\partial{y_{33}^2}} \cdot w_{32}^2 \\ \frac{\partial{L_4}}{\partial{y_{41}^2}} \cdot w_{11}^2 + \frac{\partial{L_4}}{\partial{y_{42}^2}} \cdot w_{21}^2 + \frac{\partial{L_4}}{\partial{y_{43}^2}} \cdot w_{31}^2 & \frac{\partial{L_4}}{\partial{y_{41}^2}} \cdot w_{12}^2 + \frac{\partial{L_4}}{\partial{y_{42}^2}} \cdot w_{22}^2 + \frac{\partial{L_4}}{\partial{y_{43}^2}} \cdot w_{32}^2 \\ \vdots & \vdots \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}}} & \frac{\partial{L_1}}{\partial{y_{12}}} & \frac{\partial{L_1}}{\partial{y_{13}}} \\ \frac{\partial{L_2}}{\partial{y_{21}}} & \frac{\partial{L_2}}{\partial{y_{22}}} & \frac{\partial{L_2}}{\partial{y_{23}}} \\ \frac{\partial{L_3}}{\partial{y_{31}}} & \frac{\partial{L_3}}{\partial{y_{32}}} & \frac{\partial{L_3}}{\partial{y_{33}}} \\ \frac{\partial{L_4}}{\partial{y_{41}}} & \frac{\partial{L_4}}{\partial{y_{42}}} & \frac{\partial{L_4}}{\partial{y_{43}}} \\ \vdots & \vdots & \vdots \end{pmatrix} \begin{pmatrix} w_{11}^2 & w_{12}^2 \\ w_{21}^2 & w_{22}^2 \\ w_{31}^2 & w_{32}^2 \\ \end{pmatrix} \\ &= dE2 \cdot W_2^\top \\ &\Rightarrow E1 \end{align*}

10. 逆伝播 - 出力層における損失関数の重みによる偏微分計算

dW2 = np.dot(A1.T, dE2) / N

損失関数 L の重み W2 に対する偏微分を算出する。

\begin{align*} \frac{\partial{L_i}}{\partial{W2}} &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{w_{11}^2}} & \frac{\partial{L_i}}{\partial{w_{21}}^2} & \frac{\partial{L_i}}{\partial{w_{31}}^2} \\ \frac{\partial{L_i}}{\partial{w_{12}^2}} & \frac{\partial{L_i}}{\partial{w_{22}}^2} & \frac{\partial{L_i}}{\partial{w_{32}}^2} \\ \end{pmatrix} \\ \frac{\partial{L_i}}{\partial{w_{11}^2}} &= \frac{\partial{L_i}}{\partial{f(w_{11}^2,w_{12}^2,w_{13}^2,w_{21}^2,w_{22}^2,w_{23}^2)}} \cdot \frac{\partial{f(w_{11}^2,w_{12}^2,w_{13}^2,w_{21}^2,w_{22}^2,w_{23}^2)}}{\partial{w_{11}^2}} \\ &= \frac{\partial{L_i}}{\partial{Y_i}} \cdot \frac{\partial{Y_i}}{\partial{w_{11}^2}} \end{align*}

ここで、ジャコビアンの連鎖律および

\begin{bmatrix} y_{11}^2 &= a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2 \\ y_{12}^2 &= a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2 \\ y_{13}^2 &= a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2 \\ \end{bmatrix}

であることから、

\begin{align*} \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{w_{11}^2}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{w_{11}^2}} \\ \frac{\partial{y_{12}^2}}{\partial{w_{11}^2}} \\ \frac{\partial{y_{13}^2}}{\partial{w_{11}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{w_{11}^2}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{w_{11}^2}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{w_{11}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{w_{11}^2}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{w_{11}^2}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{w_{11}^2}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot a_{11}^1 + 0 + 0 \\ \end{pmatrix} \\ &= \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot a_{11}^1 \\ \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{w_{21}^2}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{w_{21}^2}} \\ \frac{\partial{y_{12}^2}}{\partial{w_{21}^2}} \\ \frac{\partial{y_{13}^2}}{\partial{w_{21}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{w_{21}^2}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{w_{21}^2}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{w_{21}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{w_{21}^2}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{w_{21}^2}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{w_{21}^2}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} 0 + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot a_{11}^1 + 0 \\ \end{pmatrix} \\ &= \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot a_{11}^1 \\ \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{w_{12}^2}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{w_{12}^2}} \\ \frac{\partial{y_{12}^2}}{\partial{w_{12}^2}} \\ \frac{\partial{y_{13}^2}}{\partial{w_{12}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{w_{12}^2}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{w_{12}^2}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{w_{12}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{w_{12}^2}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{w_{12}^2}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{w_{12}^2}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot a_{12}^1 + 0 + 0 \\ \end{pmatrix} \\ &= \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot a_{12}^1 \\ \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{w_{22}^2}} &= \dots \end{align*}

これを代入すると、

\begin{align*} \frac{\partial{L_i}}{\partial{W2}} &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{w_{11}^2}} & \frac{\partial{L_i}}{\partial{w_{21}}^2} & \frac{\partial{L_i}}{\partial{w_{31}}^2} \\ \frac{\partial{L_i}}{\partial{w_{12}^2}} & \frac{\partial{L_i}}{\partial{w_{22}}^2} & \frac{\partial{L_i}}{\partial{w_{32}}^2} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{Y_{i}}} \cdot \frac{\partial{Y_{i}}}{\partial{w_{11}^2}} & \frac{\partial{L_i}}{\partial{Y_{i}}} \cdot \frac{\partial{Y_{i}}}{\partial{w_{21}^2}} & \frac{\partial{L_i}}{\partial{Y_{i}}} \cdot \frac{\partial{Y_{i}}}{\partial{w_{31}^2}} \\ \frac{\partial{L_i}}{\partial{Y_{i}}} \cdot \frac{\partial{Y_{i}}}{\partial{w_{12}^2}} & \frac{\partial{L_i}}{\partial{Y_{i}}} \cdot \frac{\partial{Y_{i}}}{\partial{w_{22}^2}} & \frac{\partial{L_i}}{\partial{Y_{i}}} \cdot \frac{\partial{Y_{i}}}{\partial{w_{32}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{y_{i1}^2}} \cdot a_{i1}^1 & \frac{\partial{L_i}}{\partial{y_{i2}^2}} \cdot a_{i1}^1 & \frac{\partial{L_i}}{\partial{y_{i3}^2}} \cdot a_{i1}^1 \\ \frac{\partial{L_i}}{\partial{y_{i1}^2}} \cdot a_{i2}^1 & \frac{\partial{L_i}}{\partial{y_{i2}^2}} \cdot a_{i2}^1 & \frac{\partial{L_i}}{\partial{y_{i3}^2}} \cdot a_{i2}^1 \\ \end{pmatrix} \\ &= \begin{pmatrix} a_{i1}^1 \\ a_{i2}^1 \\ \end{pmatrix} \begin{pmatrix} \frac{\partial{L_i}}{\partial{y_{i1}^2}} & \frac{\partial{L_i}}{\partial{y_{i2}^2}} & \frac{\partial{L_i}}{\partial{y_{i3}^2}} \\ \end{pmatrix} \\ &= A1_{i}^\top \cdot dE2_{i} \\ \frac{\partial{L}}{\partial{W2}} &= \begin{pmatrix} a_{11}^1 & a_{21}^1 & a_{31}^1 & a_{41}^1 & \dots \\ a_{12}^1 & a_{22}^1 & a_{32}^1 & a_{42}^1 & \dots \\ \end{pmatrix} \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \frac{\partial{L_2}}{\partial{y_{21}^2}} & \frac{\partial{L_2}}{\partial{y_{22}^2}} & \frac{\partial{L_2}}{\partial{y_{23}^2}} \\ \frac{\partial{L_3}}{\partial{y_{31}^2}} & \frac{\partial{L_3}}{\partial{y_{32}^2}} & \frac{\partial{L_3}}{\partial{y_{33}^2}} \\ \frac{\partial{L_4}}{\partial{y_{41}^2}} & \frac{\partial{L_4}}{\partial{y_{42}^2}} & \frac{\partial{L_4}}{\partial{y_{43}^2}} \\ \vdots & \vdots & \vdots \end{pmatrix} \\ &= A1^\top \cdot dE2 \\ \frac{1}{N} \cdot \frac{\partial{L}}{\partial{W2}} &= \frac{1}{N} \cdot A1^\top \cdot dE2 \\ &\Rightarrow dW2 \end{align*}

11. 逆伝播 - 出力層における損失関数のバイアスによる偏微分計算

dB2 = dE2.sum(axis=0) / N

損失関数 L のバイアス B2 に対する偏微分を算出する。

\begin{align*} \frac{\partial{L_i}}{\partial{b^2}} &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{b_{1}^2}} & \frac{\partial{L_i}}{\partial{b_{2}}^2} & \frac{\partial{L_i}}{\partial{b_{3}}^2} \\ \end{pmatrix} \\ \frac{\partial{L_i}}{\partial{b_{1}^2}} &= \frac{\partial{L_i}}{\partial{f(b_{1}^2,b_{2}^2,b_{3}^2)}} \cdot \frac{\partial{f(b_{1}^2,b_{2}^2,b_{3}^2)}}{\partial{b_{1}^2}} = \frac{\partial{L_i}}{\partial{Y_i}} \cdot \frac{\partial{Y_i}}{\partial{b_{1}^2}} \end{align*}

ここで、ジャコビアンの連鎖律および

\begin{bmatrix} y_{11}^2 &= a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2 \\ y_{12}^2 &= a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2 \\ y_{13}^2 &= a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2 \\ \end{bmatrix}

であることから、

\begin{align*} \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{b_{1}^2}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{b_{1}^2}} \\ \frac{\partial{y_{12}^2}}{\partial{b_{1}^2}} \\ \frac{\partial{y_{13}^2}}{\partial{b_{1}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{b_{1}^2}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{b_{1}^2}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{b_{1}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{b_{1}^2}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{b_{1}^2}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{b_{1}^2}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot 1 + 0 + 0 \\ \end{pmatrix} \\ &= \frac{\partial{L_1}}{\partial{y_{11}^2}} \\ \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{b_{2}^2}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{b_{2}^2}} \\ \frac{\partial{y_{12}^2}}{\partial{b_{2}^2}} \\ \frac{\partial{y_{13}^2}}{\partial{b_{2}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{b_{2}^2}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{b_{2}^2}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{b_{2}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{b_{2}^2}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{b_{2}^2}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{b_{2}^2}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} 0 + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot 1 + 0 \\ \end{pmatrix} \\ &= \frac{\partial{L_1}}{\partial{y_{12}^2}} \\ \frac{\partial{L_1}}{\partial{Y_{1}}} \cdot \frac{\partial{Y_{1}}}{\partial{b_{3}^2}} &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} & \frac{\partial{L_1}}{\partial{y_{12}^2}} & \frac{\partial{L_1}}{\partial{y_{13}^2}} \\ \end{pmatrix} \cdot \begin{pmatrix} \frac{\partial{y_{11}^2}}{\partial{b_{3}^2}} \\ \frac{\partial{y_{12}^2}}{\partial{b_{3}^2}} \\ \frac{\partial{y_{13}^2}}{\partial{b_{3}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{y_{11}^2}}{\partial{b_{3}^2}} + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{y_{12}^2}}{\partial{b_{3}^2}} + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{y_{13}^2}}{\partial{b_{3}^2}} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot \frac{\partial{}}{\partial{b_{3}^2}}(a_{11}^1 \cdot w_{11}^2 + a_{12}^1 \cdot w_{12}^2 + b_{1}^2) + \frac{\partial{L_1}}{\partial{y_{12}^2}} \cdot \frac{\partial{}}{\partial{b_{3}^2}}(a_{11}^1 \cdot w_{21}^2 + a_{12}^1 \cdot w_{22}^2 + b_{2}^2) + \frac{\partial{L_1}}{\partial{y_{13}^2}} \cdot \frac{\partial{}}{\partial{b_{3}^2}}(a_{11}^1 \cdot w_{31}^2 + a_{12}^1 \cdot w_{32}^2 + b_{3}^2) \\ \end{pmatrix} \\ &= \begin{pmatrix} 0 + 0 + \frac{\partial{L_1}}{\partial{y_{11}^2}} \cdot 1 \\ \end{pmatrix} \\ &= \frac{\partial{L_1}}{\partial{y_{13}^2}} \end{align*}

これを代入すると、

\begin{align*} \frac{\partial{L_i}}{\partial{b^2}} &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{b_{1}^2}} & \frac{\partial{L_i}}{\partial{b_{2}}^2} & \frac{\partial{L_i}}{\partial{b_{3}}^2} \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{Y_i}} \cdot \frac{\partial{Y_i}}{\partial{b_{1}^2}} & \frac{\partial{L_i}}{\partial{Y_i}} \cdot \frac{\partial{Y_i}}{\partial{b_{2}^2}} & \frac{\partial{L_i}}{\partial{Y_i}} \cdot \frac{\partial{Y_i}}{\partial{b_{3}^2}} \end{pmatrix} \\ &= \begin{pmatrix} \frac{\partial{L_i}}{\partial{y_{i1}^2}} & \frac{\partial{L_i}}{\partial{y_{i2}^2}} & \frac{\partial{L_i}}{\partial{y_{i3}^2}} \\ \end{pmatrix} \\ &= dE2_{i} \\ \frac{\partial{L}}{\partial{b_2}} &= \sum_{i=1}^{N}{\begin{pmatrix} \frac{\partial{L_i}}{\partial{y_{i1}^2}} & \frac{\partial{L_i}}{\partial{y_{i2}^2}} & \frac{\partial{L_i}}{\partial{y_{i3}^2}} & ,axis=0 \\ \end{pmatrix}} \\ &= \begin{pmatrix} \displaystyle\sum_{i=1}^{N}{\frac{\partial{L_i}}{\partial{y_{i1}^2}}} & \displaystyle\sum_{i=1}^{N}{\frac{\partial{L_i}}{\partial{y_{i2}^2}}} & \displaystyle\sum_{i=1}^{N}{\frac{\partial{L_i}}{\partial{y_{i3}^2}}} \\ \end{pmatrix} \\ \frac{1}{N} \cdot \frac{\partial{L}}{\partial{b_2}} &= \frac{1}{N} \begin{pmatrix} \displaystyle\sum_{i=1}^{N}{\frac{\partial{L_i}}{\partial{y_{i1}^2}}} & \displaystyle\sum_{i=1}^{N}{\frac{\partial{L_i}}{\partial{y_{i2}^2}}} & \displaystyle\sum_{i=1}^{N}{\frac{\partial{L_i}}{\partial{y_{i3}^2}}} \\ \end{pmatrix} \\ &\Rightarrow dB2 \end{align*}

12. 逆伝播 - 隠れ層における偏微分計算 (共通部分)

dE1 = E1 * A1 * (1 - A1)

損失関数 L に対する隠れ層の偏微分は、

\begin{align*} \frac{\partial{L}}{\partial{y}} &=\frac{\partial{L}}{\partial{a}} \cdot \frac{\partial{a}}{\partial{y}} \\ &=\frac{\partial{L}}{\partial{a}} \cdot \{sigmoid(y) \times (1 - sigmoid(y)) \} \end{align*}

この場合、a=A^1であることから、

\begin{align*} \frac{\partial{L}}{\partial{y}} &= \frac{\partial{L}}{\partial{A^1}} \cdot \{A^1 \times (1 - A^1) \} \\ \end{align*}

[9. 逆伝播 - 出力層における損失関数の入力による偏微分計算] より、

\begin{align*} \frac{\partial{L}}{\partial{y}} &= E1 \cdot \{A^1 \times (1 - A^1) \} \\ \end{align*}

13. 逆伝播 - 隠れ層における損失関数の重みによる偏微分計算

dW1 = np.dot(X_train.T, dE1) / N

[10. 逆伝播 - 出力層における損失関数の重みによる偏微分計算] と同様

14. 逆伝播 - 隠れ層における損失関数のバイアスによる偏微分計算

dB1 = dE1.sum(axis=0) / N

[11. 逆伝播 - 出力層における損失関数のバイアスによる偏微分計算] と同様

15. 最適化

W2 = W2 - learning_rate * dW2
B2 = B2 - learning_rate * dB2
W1 = W1 - learning_rate * dW1
B1 = B1 - learning_rate * dB1
\begin{align*} w &\leftarrow w-\eta\frac{\partial{L}}{\partial{w}} \\\\ b &\leftarrow b-\eta\frac{\partial{L}}{\partial{b}} \end{align*}

により、重みとバイアスの最適化を行う。

まとめ

以上、20年以上前に学んだ数学を思い出しながら計算過程をお復習いしました。
間違いなどあれば、ぜひご教授ください！

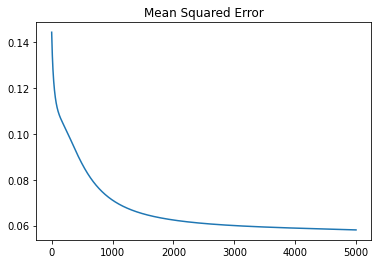
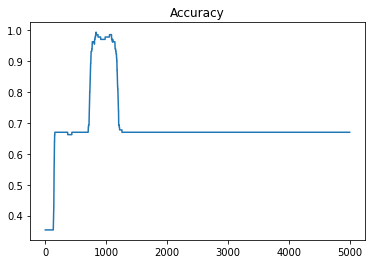
コードはまとめると次のようになり、学習回数を重ねる毎に偏微分の値がゼロに近いて最適化が進んでいきます。

for itr in range(iterations):
    # Implementing feedforward propagation on hidden layer
    Z1 = np.dot(X_train, W1) + B1
    A1 = sigmoid(Z1)

    # Implementing feedforward propagation on output layer
    Z2 = np.dot(A1, W2) + B2
    A2 = sigmoid(Z2)

    # Backpropagation phase
    E2 = A2 - np.identity(3)[y_train]
    dE2 = E2 * A2 * (1 - A2)

    E1 = np.dot(dE2, W2.T)
    dE1 = E1 * A1 * (1 - A1)

    # Updating the weights
    dW2 = np.dot(A1.T, dE2) / N
    dB2 = dE2.sum(axis=0) / N
    dW1 = np.dot(X_train.T, dE1) / N
    dB1 = dE1.sum(axis=0) / N

    W2 = W2 - learning_rate * dW2
    B2 = B2 - learning_rate * dB2
    W1 = W1 - learning_rate * dW1
    B1 = B1 - learning_rate * dB1


コード全体はこちら。
# ## 1. Import Libraries
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# ## 2. Load the Dataset
# Loading dataset
data = load_iris()
# Dividing the dataset into target variable and features
X=data.data
y=data.target

# ## 3. Split Dataset in Training and Testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20, random_state=4)

# ## 4. Initialize the hyperparameters
learning_rate = 0.1
iterations = 5000
N = y_train.size
# Input features
input_size = 4
# Hidden layers 
hidden_size = 2
# Output layer
output_size = 3
results = pd.DataFrame(columns=['mse', 'accuracy'])

# ## 5. Initialize Weights
np.random.seed(10)
# Hidden layer
W1 = np.random.normal(scale=0.5, size=(input_size, hidden_size))
B1 = np.random.normal(scale=0.5, size=hidden_size)
W1_baias = np.vstack([W1, B1])
# Output layer
W2 = np.random.normal(scale=0.5, size=(hidden_size, output_size))
B2 = np.random.normal(scale=0.5, size=output_size)
W2_baias = np.vstack([W2, B2])

# ## 6. Define helper functions
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def mean_squared_error(y_pred, y_true):
    return ((y_pred - y_true)**2).sum() / (2*y_pred.size)

def accuracy(y_pred, y_true):
    acc = y_pred.argmax(axis=1) == y_true.argmax(axis=1)
    return acc.mean()

# learning
for itr in range(iterations):
    # Implementing feedforward propagation on hidden layer
    Z1 = np.dot(X_train, W1) + B1
    A1 = sigmoid(Z1)

    # Implementing feedforward propagation on output layer
    Z2 = np.dot(A1, W2) + B2
    A2 = sigmoid(Z2)

    # Calculating the error
    mse = mean_squared_error(A2, np.identity(3)[y_train])
    acc = accuracy(A2, np.identity(3)[y_train])
    results=results.append({'mse':mse, 'accuracy':acc}, ignore_index=True)

    # Backpropagation phase
    E2 = A2 - np.identity(3)[y_train]
    dE2 = E2 * A2 * (1 - A2)

    E1 = np.dot(dE2, W2.T)
    dE1 = E1 * A1 * (1 - A1)

    # Updating the weights
    dW2 = np.dot(A1.T, dE2) / N
    dB2 = dE2.sum(axis=0) / N
    dW1 = np.dot(X_train.T, dE1) / N
    dB1 = dE1.sum(axis=0) / N

    W2 = W2 - learning_rate * dW2
    B2 = B2 - learning_rate * dB2
    W1 = W1 - learning_rate * dW1
    B1 = B1 - learning_rate * dB1

results.mse.plot(title='Mean Squared Error')
results.accuracy.plot(title='Accuracy')

参考 (感謝です！)

https://www.ccn.yamanashi.ac.jp/~tmiyamoto/img/matrixform_mlp.pdf
https://ieyasu03.web.fc2.com/Deep_Learning/7-BackProp.pdf
https://imagingsolution.net/deep-learning/backpropagation/
https://www.bigdata-navi.com/aidrops/2810/
https://blog.regonn.tokyo/data-science/2017-10-27-deep-learning/
https://www2.kaiyodai.ac.jp/~takenawa/learning/
https://atmarkit.itmedia.co.jp/ait/articles/2202/09/news027.html

Discussion