🔢
エルミート標準形のアルゴリズム

ishimaru_exwzd
2025/12/04に公開
エンタープライズソリューション事業ユニット (ESU) の石丸です。エクサウィザーズ Advent Calendar 2025 4日目の記事です。

 はじめに線形方程式系 Ax = b を解くというのは、線形代数の基本的な問題です。実数や有理数の範囲であればガウスの消去法で効率的に解けますが、整数解のみを求めたいという場合はどうでしょうか。
整数係数の方程式の整数解を求める問題はディオファントス方程式と呼ばれ、実数の場合とは異なる困難があります。本記事では、線形ディオファントス方程式系 Ax = b (A \in \mathbb{Z}^{m \times n}, b \in \mathbb{Z}^m) を整数上で解くための数学的な道具であるエルミート標準形と、それを多項式時間で計算するアルゴリズムについて解説します。
この記事は 2 年前に社内の勉強会で扱った内容を記事化したものです。アルゴリズムの実装に必要なことが不足なく全部書いてある資料が見つからなかったのがこれを書いた動機の一つですが、主要な部分については Eisenbrand (2010) と Micciancio (2014) の講義資料をベースにしています。証明は基本的に省略しているため、これらの資料を参照いただけると幸いです。

 拡張ユークリッド互除法まずは最も単純な 2 変数の例から始めましょう。
問題: ax + by = c の整数解 (x, y) を求めよ。
この問題については以下のことが知られています:

c が \gcd(a, b) の倍数のとき、またその時に限って整数解が存在する
具体的な解は拡張ユークリッド互除法で高速に求まる
例 (Wikipediaより): \gcd(1071, 1029) を求めよ。また、1071x + 1029y = \gcd(1071, 1029) を満たす整数の対 (x, y) を一つ求めよ。
ユークリッドの互除法を適用すると
1071 = 1029 \cdot 1 + 42
1029 = 42 \cdot 24 + 21
42 = 21 \cdot 2 + 0
より、\gcd(1071, 1029) = 21。また、逆にたどると
21 = 1029 - 42 \cdot 24 = 1029 - (1071 - 1029) \cdot 24 = 1071 \cdot (-24) + 1029 \cdot 25から x = -24, y = 25 が求まります。
このように 2 変数の場合は拡張ユークリッド互除法で高速に解けます。以降は一般の m \times n 行列 A に対する Ax = b の整数解について考えていきます。

 実数の場合の復習整数の場合を考える前に、まず実数の場合の解法を振り返ります。A が特殊な階段型になっていれば Ax=b は簡単に解けるのでした。以下の例を考えます。

\begin{bmatrix}
1 & 1 & 0 & -2 \\
0 & 2 & 3 & 4 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0
\end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ x_4\end{bmatrix} = \begin{bmatrix} -3 \\ 4 \\ 2 \\ 0\end{bmatrix}
この場合、x_4, x_3, x_2, x_1 の順に決めていけます:
x_4 = 2
自由度があるので x_3 = \alpha としておく
x_2 = (4 - 3x_3 - 4 x_4) / 2 = -2 - (3/2)\alpha
x_1 = -3 - x_2 + 2 x_4 = 3 + (3/2)\alpha
従って、\{(3 + (3/2)\alpha, -2 - (3/2)\alpha, \alpha, 2) : \alpha \in \mathbb{R}\} が解空間です。
「階段型」には行階段形と列階段形があり、それぞれ次のような見た目の行列を指します。* は任意の非ゼロ成分を表します。

\begin{bmatrix}* & * & * & * \\
0 & * & * & * \\
0 & 0 & 0 & * \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix} \begin{bmatrix}* & 0 & 0 & 0 \\ * & 0 & 0 & 0 \\ * & * & 0 & 0 \\ * & * & * & 0 \\ * & * & * & 0
\end{bmatrix}
特徴を言葉で説明すると、以下のようになります。
各行/各列の先頭の非ゼロ成分の位置が行階段形では右に、列階段形では下にずれていく。
ゼロベクトルが後ろに固まっている。
実数行列は次の行基本変形/列基本変形を繰り返すことによって行階段形/列階段形に変形できるというのがガウスの消去法でした。
行基本変形は、以下の 3 つの操作です:
二つの行を入れ替える
ある行に 0 でない定数を掛ける
ある行の定数倍を他の行に加える
列基本変形は、以下の 3 つの操作です:
二つの列を入れ替える
ある列に 0 でない定数を掛ける
ある列の定数倍を他の列に加える
基本変形を使って Ax = b を実数上で解く 2 通りの方法を整理すると以下のようになります。
行基本変形による解法:
行基本変形で A を行階段形に変換する。つまり、ある正則行列 P を左から掛けて PA を行階段形にする。

PAx = Pb を解く。PA が行階段形なので簡単。P は正則なので、この方程式の解集合と Ax = b の解集合は同じ。
列基本変形による解法:
列基本変形で A を列階段形に変換する。つまり、ある正則行列 Q を右から掛けて AQ を列階段形にする。

y = Q^{-1}x とすると Ax = AQQ^{-1}x = AQy なので、AQy = b を解く。AQ が列階段形なので簡単。

x = Qy に基づいて x を復元する。

 整数の場合の困難上の方法を整数の場合にも適用できるか考えてみます。

 困難 1: 行階段形では解きにくい行階段形の場合、実数なら簡単に解けますが、整数の場合はそうとは限りません。例えば以下の方程式系を考えます:

\begin{bmatrix}
1 & -3 & 1 \\
-1 & 3 & -1 \\
-2 & 3 & 2 \\
\end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix}
= \begin{bmatrix} -2 \\ 2 \\ -1 \end{bmatrix}
行基本変形を適用すると以下のようになります。

\begin{bmatrix}
1 & -3 & 1 \\
0 & -3 & 4 \\
0 & 0 & 0 \\
\end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ x_3\end{bmatrix}
= \begin{bmatrix} -2 \\ -5 \\ 0 \end{bmatrix}
自由度があるのでx_3 = \alphaとすると、2 行目から x_2 = (4\alpha + 5) / 3 となりますが、\alpha が整数でも x_2 が整数にならない可能性があります。
一方、列階段形だったら解けそうです:

\begin{bmatrix}
1 & 0 & 0 \\
-1 & 0 & 0 \\
-2 & 1 & 0 \\
\end{bmatrix} \begin{bmatrix}y_1 \\ y_2 \\ y_3\end{bmatrix}
= \begin{bmatrix} -2 \\ 2 \\ 1\end{bmatrix}
順に y_1 = -2, y_2 = -3, y_3 は任意の整数と求まります。列階段形では自由度を表現する 1 つのパラメータが 1 つの未知変数に対応してそれ以外には現れないため、整数の場合でも解集合が自明になります。

 困難 2: 列基本変形すると異なるディオファントス方程式になるしかし、列基本変形にも問題があります。
例えば x_1 + 2x_2 = 3 の 2 列目を 2 倍 (列基本変形) した y_1 + 4y_2 = 3 について考えます。x_1 + 2x_2 = 3 の実数解は y_1 + 4y_2 = 3 の実数解と x_1 = y_1, x_2 = 2y_2 で対応します。「対応」というのはつまり、一方の解空間がもう一方の解空間の線形変換によって得られるということです。しかし、x_1 + 2x_2 = 3 の整数解である x_1=1, x_2=1 は y_1 + 4y_2 = 3 の整数解と「対応」しません。
つまり、列基本変形をするとディオファントス方程式として等価でなくなることがあるということです。線形代数的な考察のみで整数の場合を扱うのは難しいことがわかります。より端的に、次の例を考えます。
例: 二次元ベクトル \begin{bmatrix} 2 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 2 \end{bmatrix} によって生成される空間は？
実数上であれば これは \mathbb{R}^2 そのものであり、ここにさらに別のベクトル \begin{bmatrix} 1 \\ 0 \end{bmatrix} を加えても変わりません。一方、整数上では \begin{bmatrix} 1 \\ 0 \end{bmatrix} を加えると表せる点が増えてしまいます。整数は体ではないため、線形独立性のような線形代数の概念だけでは不十分ということでしょう。そこで格子論 (lattice theory) が必要になります。

 格子
 格子とは定義: 行列 B \in \mathbb{R}^{m \times n} が与えられたとき、

\mathcal{L}(B) = \{Bx : x \in \mathbb{Z}^n\}

を B の生成する 格子 (lattice) と呼ぶ。[1]
言い換えれば、列ベクトル b_1, b_2, \ldots, b_n \in \mathbb{R}^m が与えられたとき、これらの整数線形結合で得られるベクトルの集合

\mathcal{L}(b_1, \ldots, b_n) = \left\{\sum_{j=1}^n x_j b_j : x_j \in \mathbb{Z}\right\}

が格子です。
上の図は、ベクトル (1, 2) と (-2, 5) によって生成される格子を視覚化したものです。

 格子の基底定義: 格子 \mathcal{L} が線形独立な b_1, \ldots, b_n \in \mathbb{R}^m によって生成されるとき、b_1, \ldots, b_n を \mathcal{L} の基底と呼ぶ。
また、基底ベクトルを列ベクトルとする行列 B = (b_1, \ldots, b_n) も同様に基底と呼ぶことがあります。
注意として、格子の基底は一意ではないということがあります。例えば

\mathcal{L}\left(\binom{1}{2}, \binom{-2}{5}\right) = \mathcal{L}\left(\binom{5}{1}, \binom{6}{3}\right)

です。下図は、同じ格子を生成する 2 つの異なる基底を示しています。

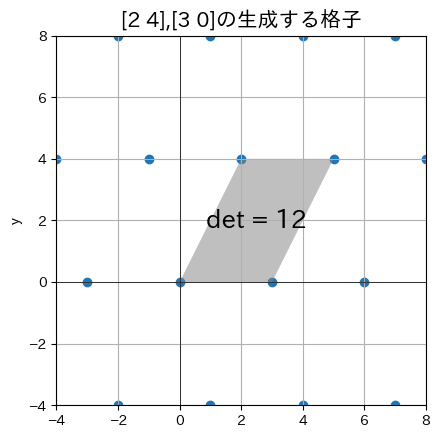
 格子の determinant定義: B が格子 \mathcal{L} の基底であるとき、その行列式の絶対値 |\det B| を \mathcal{L} の determinant と呼ぶ。この値は基底 B の選び方によらない。 [2]
!線形代数の復習: B = (b_1, \ldots, b_n) の張る平行体の（符号付き）体積は \det B に等しい。
上の図は、格子の基底が張る平行体（基本平行体）を示しています。この平行体の面積が格子の determinant です。
格子の determinant は、格子点の密度を表す量と解釈できます。determinant が大きいほど格子点がまばらで、小さいほど密になります。

 ユニモジュラ操作と行列行基本変形/列基本変形に代わる、格子を保つ操作を考えます。ベクトル a_1, \ldots, a_n が与えられたとき、これらの生成する格子を保つ操作は以下であることが知られています:

a_i の整数倍を別の a_j に足す
a_i に -1 を掛ける

a_i, a_j を入れ替える
これらを任意に有限回繰り返す操作を ユニモジュラ操作 (unimodular operation) と呼びます。行列についても同じように列に対するユニモジュラ操作が定義されます。
定義: 整数正方行列で行列式が \pm 1 であるものを ユニモジュラ行列 (unimodular matrix) と呼ぶ。
ユニモジュラ行列とユニモジュラ操作については以下の性質が成り立ちます。
ユニモジュラ操作/行列は、ユニモジュラ行列を右から掛けると（列に対する）ユニモジュラ操作になるという形で 1 対 1 対応する。
任意のユニモジュラ行列は単位行列に対するユニモジュラ操作で得られる。
ユニモジュラ行列の逆行列はユニモジュラ行列。
仮にユニモジュラ行列 U を掛けて AU を列階段形に変換できたとすると、列基本変形による解法が使えます:

y = U^{-1}x とすると Ax = AUU^{-1}x = AUy。AUy = b を解く。AU が列階段形なので簡単。

x = Uy に基づいて x を復元する。
つまり、列に対するユニモジュラ操作で A を列階段形に変換できればよいことになります。

 エルミート標準形定理: 任意の整数行列 A についてユニモジュラ行列 U が存在して、H = AU が次の条件を満たす。また、条件を満たす H はただ一つに定まる。H を A のエルミート標準形 (Hermite normal form, HNF) と呼ぶ。以下、ピボットとは各列の先頭の非ゼロ成分を指す。

H は列階段形である
ピボットの存在する行の成分はピボット自身を含めて全て非負である
ピボットとなる成分はその行の他の成分よりも真に大きい
例:

\begin{bmatrix}
0 & 0 & 0 & 0 & 0 \\
\textcircled 8 & 0 & 0 & 0 & 0 \\
-3 & 0 & 0 & 0 & 0 \\
1 & \textcircled 3 & 0 & 0 & 0 \\
2 & 0 & \textcircled 4 & 0 & 0 \\
-4 & 2 & -1 & 0 & 0
\end{bmatrix}
この行列では、2 行目の 8、4 行目の 3、5 行目の 4 がピボットです。
m \times n 行列 A が行フルランク (i.e. すべての行ベクトルが線形独立) の場合、エルミート標準形は m 本の非ゼロ列ベクトルからなります。
例:

\begin{bmatrix}
1 & 0 & 0 & 0 & 0 \\
8 & 10 & 0 & 0 & 0 \\
3 & 0 & 4 & 0 & 0 \\
1 & 3 & 0 & 5 & 0
\end{bmatrix}
このとき、格子の determinant は \det H = 1 \times 10 \times 4 \times 5 = 200 になります。 [3]
以降、行フルランクな行列に絞って、エルミート標準形を求める素朴なアルゴリズムについて考えます。つまり、各行について以下を繰り返します:
互除法でピボットの右をすべてゼロにする
ピボットの左からピボット列を引いてピボット以下にする
例としてある行列のある行 \begin{bmatrix} 5 & 18 & 12 & 8 \end{bmatrix} を 2 列目をピボットとして整理することを考えます。
2 列目と 3 列目で互除法を行うと \gcd(18, 12) = 6 が残る: \begin{bmatrix} 5 & 6 & 0 & 8 \end{bmatrix}
2 列目と 4 列目で互除法を行うと、この行を \begin{bmatrix} 5 & 2 & 0 & 0 \end{bmatrix} にできる
1 列目から 2 列目の 2 倍を引いて、ピボット以下の値にするとこの行は \begin{bmatrix} 1 & 2 & 0 & 0 \end{bmatrix}
疑似コードで表すと以下のようになります。
for i ← 1, ..., m
  for j ← i + 1, ..., n
    if A[i,j] ≠ 0
      拡張ユークリッド互除法で A[i,i]x + A[i,j]y = gcd(A[i,i], A[i,j]) となる x, y を求める
      列 i, j を [[x, -A[i,j]/gcd], [y, A[i,i]/gcd]] を右から掛けて変換
  if A[i,i] < 0 なら列 i を -1 倍
  for j ← 1, ..., i - 1
    A[i,j] を A[i,i] で割った商と余りを q, r として列 j, i を [[1, 0], [-q, 1]] を右から掛けて変換
素朴なアルゴリズムの計算量を考えます。

O(m^2n) 回の算術演算と O(mn) 回の拡張ユークリッド互除法を要する
ユニモジュラ行列 U を陽に求めたい場合は O(mn^2) 回の算術演算が必要
これを見ると多項式時間で解けそうに見えますが、計算中に現れる整数が指数的に大きくなることがあるため、多項式時間アルゴリズムではありません (Fang & Havas, 1997)。
最悪計算量が悪くても実践的には十分速いということはありえますが、実装してみるとランダム行列に対してもあまり速いとは言えないようでした。
行列によって計算時間のバラつきが大きいですが、絶対値 100 以下の 35 \times 35 のランダム整数行列に対して 8.5 秒、40 \times 40 だと 1 分以上を要するというような増え方でした。また、計算中に現れる整数が非常に大きくなり、成分の絶対値が 10 以下の 5 \times 5 行列に適用する場合でも 64 ビット整数を超えることがありました。

 多項式時間アルゴリズム多項式時間であること以外も考慮した理想的なアルゴリズムの性質としては以下がありそうです。ここではこれらを満たすアルゴリズムについて考えていきます。
計算中に登場する整数の大きさが入力の多項式サイズに抑えられる。
計算の途中で有理数型を必要としない。つまり、fraction-free なアルゴリズムである。
行フルランクとは限らない一般の行列に対してエルミート標準形を求められる。
エルミート標準形に変換するためのユニモジュラ行列 U も同時に求められる。

 計算に現れる整数の大きさを抑える定理 (Schrijver, 1986): m \times n 行列 A の生成する格子 \mathcal{L}(A) の determinant を D とする。D の倍数である任意の整数 d について、A の右に単位行列 I の d 倍を追加した m \times (n + m) 行列 [A | dI] の生成する格子は \mathcal{L}(A) と同一である。
例:

\left[\begin{array}{ccccc|cccc}
1 & 0 & 0 & 0 & 1 & 200 & 0 & 0 & 0 \\
8 & 10 & 0 & 10 & -2 & 0 & 200 & 0 & 0\\
3 & 0 & 4 & 0 & 3 & 0 & 0 & 200 & 0\\
1 & 3 & 0 & 8 & -2 & 0 & 0 & 0 & 200\\
\end{array}\right]
A の代わりに [A|dI] に対してアルゴリズムを適用すると、計算に現れる整数の大きさを d の定数乗程度に抑えることができます。また、アルゴリズム上は陽に dI を追加せずに、計算中に適切なタイミングで \bmod d を取ればよさそうです。
しかし、2 つ問題があります:
格子の determinant が事前にはわからない。
エルミート標準形が求まれば determinant も求まるが…？


A の代わりに [A|dI] に対するユニモジュラ操作を行うため、H = AU を満たすユニモジュラ行列 U が同時に計算できない。
1 については、以下の事実が使えます。
事実：格子にベクトルを追加すると、determinant は元の格子の determinant の約数になる。


上の図は、格子にベクトルを追加すると格子点が増えて determinant（基本平行体の面積）が小さくなることを示しています。つまり、m \times n 行列の線形独立な列ベクトルを任意に m 本選んでその行列式を求めると、格子の determinant の倍数になっています。上の定理で必要なのは determinant そのものではなく、その倍数が１つ分かればよかったので、この方法で十分です。
行列式はガウスの消去法で求まります。線形従属と分かった列を捨てながら消去法をして、線形独立なベクトルが m 本見つかった時点でその行列式を求めればよいです。
また、2 については次の問題が解ければよいです。
問題: エルミート標準形 H が求まった後に、H = AU を満たすユニモジュラ行列 U を求めたい。
A を行フルランクの m \times n 行列 (m \le n) とします。m 本の線形独立な列ベクトルが左 m 列に固まっている場合を考えます。このとき、以下の事実が成り立ちます:

A の HNF が H である \Leftrightarrow A' := \begin{bmatrix}A \\ 0 \mid I_{n-m}\end{bmatrix} の HNF が、ある行列 B について H' := \begin{bmatrix}H \\ B \end{bmatrix} である

A'U = H' を満たすユニモジュラ行列 U は AU = H も満たす

A' は正則行列である
したがって、A' の HNF H' を求めた後、U = H' {A'}^{-1} と計算できます。

 アルゴリズムのまとめこれらをまとめると、エルミート標準形とユニモジュラ行列を求める fraction-free な多項式時間アルゴリズムは以下のように整理できます。わたしの実装例はこちらを参照してください。

A から線形独立な行ベクトルを抜き出して、行フルランクな m' \times n 行列 A' を得る
Gram-Schmidt 直交化法で可能。fraction-free なアルゴリズムは Erlingsson, Kaltofen & Musser (1996) 参照。


A' の m' 本の線形独立な列ベクトルを任意に取って構成した正方行列の行列式 d を求める
ガウスの消去法で可能。fraction-free なアルゴリズムは Bareiss (1968) 参照。


A' の下部に単位ベクトルを n - m' 本追加して n \times n 正則行列 A'' を得る。
格子の determinant の倍数 d を利用して、A'' のエルミート標準形 H'' を多項式時間で求める。H'' の最初の m' 行が A' のエルミート標準形 H' である。
最初に除いた線形従属な行は、Gram-Schmidt 直交化法の適用時にそれ以前の行の線形結合で表されているので、それに従って H' から A のエルミート標準形 H を復元する。 (Micciancio, 2014)

U = H'' {A''}^{-1} を計算して A のユニモジュラ行列 U を得る。
これも Bareiss (1968) で可能。

この流れをきちんと書いてくれている文献が見つからなかったのが記事を書いた動機の一つですが、よりスマートなやり方がある可能性はあります。

 計算量解析定理 (アダマール不等式): 実数行列 A = (a_1, a_2, \ldots, a_n) について以下が成り立つ。
|\det(A)| \le \prod_{i=1}^n \|a_i\|系: A の各成分が絶対値 B 以下の整数であるとき、|\det A| \le (B n^{1/2})^n。
系より、A の行列式は O(n\log(nB)) ビットで抑えられると言えます。
以下、簡単のために A を絶対値 B 以下の整数による n \times n 行列とします。

O(n^3) 回の算術演算と O(n^2) 回の拡張ユークリッド互除法によって A をエルミート標準形に変換できる。
計算中に現れる整数の大きさは高々格子の determinant の定数乗であり、O(n\log(nB)) ビットで抑えられる。

k ビット整数の乗算は、素朴には O(k^2)、Karatsuba 法で O(k^{1.59})、最速は O(k \log k) で可能。

k ビット整数の互除法は O(k) 回の乗算で可能。
これらをまとめると、エルミート標準形は素朴な乗算で O(n^5 \log^3(nB))、頑張れば O(n^4 \mathrm{polylog}(n, B)) で求まると言えます。

 実測多項式時間アルゴリズムの実装でランダム行列に対してエルミート標準形とユニモジュラ行列を求めました。
絶対値 100 以下の 100 \times 100 行列に対して 1.6 秒
絶対値 10^9 以下の 100 \times 100 行列に対して 7.2 秒
行フルランクとわかっている行列のエルミート標準形を求めるだけなら、絶対値 10^9 以下の 100 \times 100 行列で 2.9 秒
素朴なアルゴリズムと比較して、実測上も大幅に高速化されているようでした。

 既存研究・実装エルミート標準形のアルゴリズムの新しめの論文は例えば Birmpilis, Labahn & Storjohann (2022) で、イントロダクションからアルゴリズムの発展の歴史をたどることができます。少なくとも理論計算量についてはここで挙げたアルゴリズムより良いものが存在するようです。ただし、行列積が O(n^\omega), \omega < 3 なことを利用するものも多く、実用面での SOTA がどのアルゴリズムなのかよくわかっていません。
応用上は疎行列の場合が気になりますが、研究は多くはないようです。疎行列の場合に \mathbb{Z}^n 上で Ax = b を解く問題を扱っている研究として Giesbrecht (1997) がありました。
また、定番の高速な計算機代数ライブラリである PARI/GP にエルミート標準形を求める関数が実装されています。Python では cypari または cypari2 から使えます。cypari で絶対値 10^9 以下の 100 \times 100 行列を試してみると 0.8 秒で終わるなど、自分のものよりだいぶ速いようでした。計算機代数の有名ソフトウェアであるSageMathにもエルミート標準形を求める関数がありますが、内部で平均計算量のよい Micciancio & Warinschi (2001)を試みて、失敗したら PARI/GP を呼び出すようです。

 参考文献Bareiss, Erwin H. "Sylvester's identity and multistep integer-preserving Gaussian elimination." Mathematics of Computation 22 (1968): 565-578.
Birmpilis, Stavros, George Labahn and Arne Storjohann. "A Cubic Algorithm for Computing the Hermite Normal Form of a Nonsingular Integer Matrix." ACM Transactions on Algorithms 19 (2022): 1-36.
Cassels, John W.. “An introduction to the geometry of numbers (Reprint).” Classics in Mathematics (1997).
Conforti, Michele, Gérard Cornuéjols and Giacomo Zambelli. "Integer Programming." (2014).
Eisenbrand, Friedrich. “Integer Programming and Algorithmic Geometry of Numbers - A tutorial.” 50 Years of Integer Programming (2010).
Erlingsson, Úlfar, Erich L. Kaltofen and David R. Musser. "Generic Gram-Schmidt orthogonalization by exact division." International Symposium on Symbolic and Algebraic Computation (1996).
Fang, Xin Gui and George Havas. "On the worst-case complexity of integer Gaussian elimination." International Symposium on Symbolic and Algebraic Computation (1997).
Giesbrecht, Mark. “Efficient parallel solution of sparse systems of linear diophantine equations.” International Workshop on Parallel Symbolic Computation (1997).
Micciancio, Daniele and Bogdan Warinschi. “A linear space algorithm for computing the hermite normal form.” Electron. Colloquium Comput. Complex. TR00 (2001).
Micciancio, Daniele. "Basic Algorithms." Lecture Notes on Lattice Algorithms and Applications (2014). https://cseweb.ucsd.edu/classes/sp14/cse206A-a/lec4.pdf.
講義ノート一覧は https://cseweb.ucsd.edu/classes/sp14/cse206A-a/ から辿れます。

Schrijver, Alexander. "Theory of linear and integer programming." Wiley-Interscience series in discrete mathematics and optimization (1986).

脚注
より一般的な定義では、\mathbb R^n の部分集合 S が格子であるとは「S が通常の加法に関して \mathbb R^n の離散部分群であり、かつ \mathrm{span}(S) = \mathbb R^n であること」とされます。Wikipediaや Cassels (1997)はこの定義を採用しています。\Lambda = \{\binom{1}{2}x : x \in \mathbb Z\} のような「格子」は \mathbb R^2 の格子ではないので注意。ただ、その場合でも \Lambda を \mathbb R^2 のある部分空間の格子と呼んで問題ないと思いますし、実際、文献によっては最初から\mathbb R^n の任意の部分空間に対して格子を定義している例もありました。 ↩︎
determinant は線形代数では行列式と訳されますが、格子の文脈でそう訳すと混乱を招きそうなので英語のまま使うことにしました。 ↩︎
末尾のゼロベクトルは無視します。エルミート標準形の「一意性」を成り立たせるためには、厳密には余分なゼロベクトルを無視する必要がありました。 ↩︎