Zenn
Open3

Haskell / gloss で幾何や物理のアニメーション

Haskell
Creative Coding
えとあるえとある

［準備］gnuplot: 関数をプロットできるようにする

まず関数 y=f(x) の概形を確認できるようにするため、gnuplot で関数の描画を行う。

最初 cabal build && cabal exec run-experiment でコンパイルしたバイナリを実行しても gnuplot の描画ウィンドウが表示されてくれなかった。どうやら描画自体は haskell が別途 gnuplot のプロセスを起動しにいっているっぽく、その前に haskell プログラムが終了してしまうと gnuplot の描画ウィンドウも表示前に閉じられてしまうようだ[1]。

なので標準入力から Enter が押されるまでプログラムを idle させるようにしたらうまく描画された。

ソースコード

app/Main.hs
module Main where

import Experiments (plotSin)

main :: IO ()
main = do
    putStrLn "Experiment start!"
    Experiments.plotSin
src/Experiments.hs
module Experiments (plotSin) where

import Graphics.Gnuplot.Simple (plotFunc)

plotSin :: IO ()
plotSin = do
    plotFunc [] [0.0, 0.1..10.0] (sin :: Double -> Double)
    putStrLn "Press enter to exit..."
    _ <- getLine
    return ()

実行

executable の名前は run-experiment としている。

cabal exec run-experiment

↓

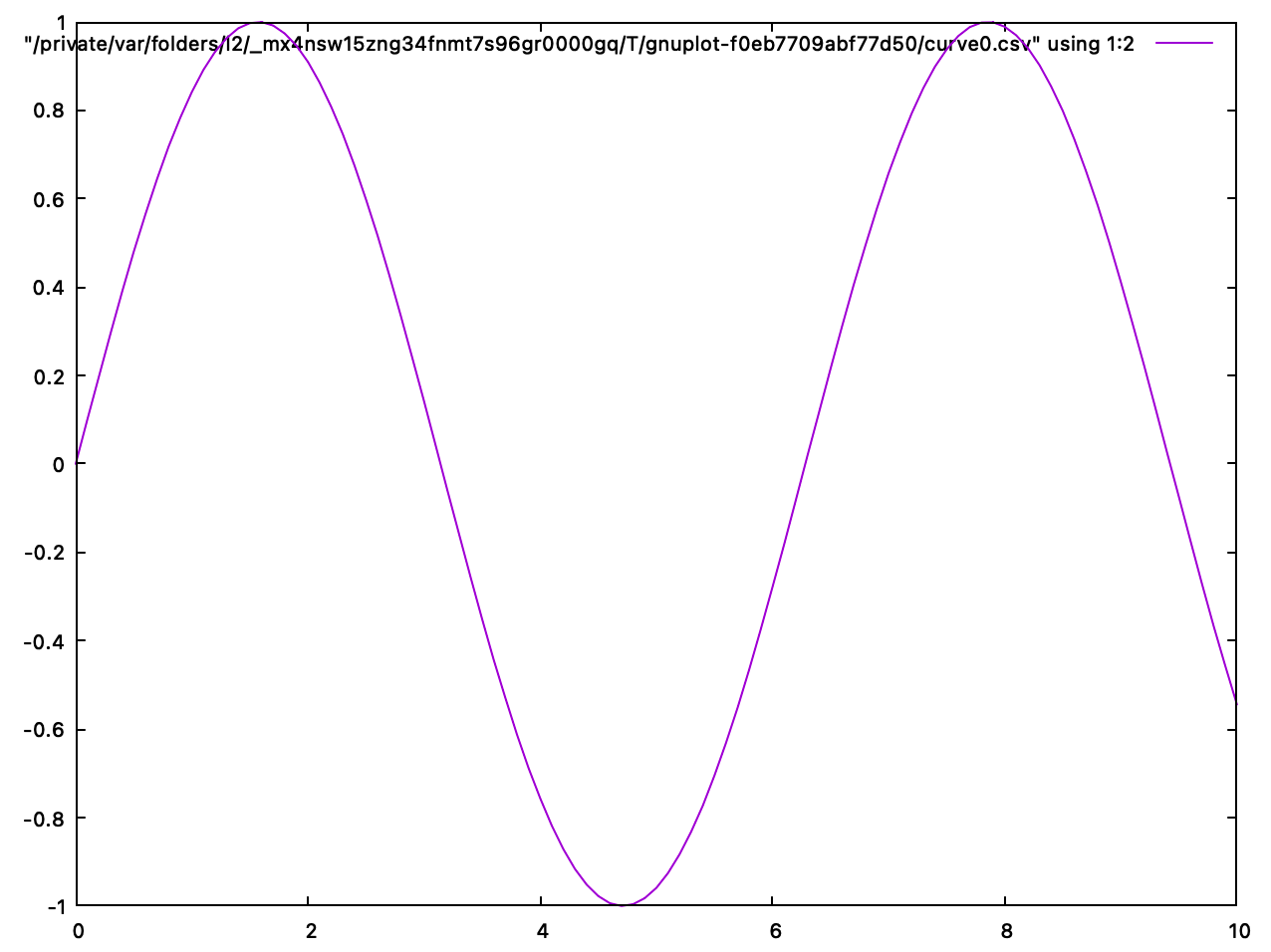
グラフの見た目とかはおいおい整えていくことにしよう。

脚注

  1. cf. https://stackoverflow.com/questions/57370426/why-haskell-gnuplot-code-works-in-ghci-but-not-from-cli-after-compiling ↩︎

えとあるえとある

[2D] 放物線軌道での自由落下

gloss で 2次元での物体の放物線軌道のアニメーションを作ってみる。

simulate

物理アニメーションの描画には Graphics.Gloss の関数 simulate を使う。simulate の型は以下の通り。

ghci> :m Graphics.Gloss
ghci> :t simulate
simulate
  :: Display                         -- (1) ディスプレイモード
     -> Color                        -- (2) 背景色
     -> Int                          -- (3) 1秒あたりの系の状態の更新頻度
     -> model                        -- (4) 系の初期状態を表す型変数
     -> (model -> Picture)           -- (5) 系の状態を描画（Picture に変換）する関数
     -> (Graphics.Gloss.Data.ViewPort.ViewPort
         -> Float -> model -> model) -- (6) 系の状態の時間発展を記述する関数
     -> IO ()

物理アニメーションとは、系の時間発展の様子を描画するプログラム である。物理学において系の時間発展は微分方程式で記述されることが多い。微分方程式というと難しそうに聞こえるが、これはプログラミングの言葉で言い換えれば「現在の系の物理量（e.g. 位置、速度、加速度など）を引数として1ステップ経過後の系の物理量を返す関数」である。

simulate では系の物理量を上記コード中の型変数 model、微分方程式に相当する関数を (6) として与える。型引数 model には物理系の現在の状態を表す型を自分で定義して与える。(6) の関数は引数が多く何やら複雑に見えるが、ViewPort には描画先ビューポート、Float には 1ステップの時間（単位：秒）が与えられ、残りの model -> model の部分が「現在の model から1ステップ後の model を計算する」に相当する型である[1]。

ソースコード（抜粋）

赤い球が放物線軌道で落下していくアニメーションを描画してみる。コードは 参考文献 [1] にあったものを一部改変。

Experiments.hs
import Graphics.Gloss (Display(InWindow), black, red, color, Picture(ThickCircle, Translate), simulate)

displayMode :: Display
displayMode = InWindow "Projectile Simulation" (800, 600) (20, 20)

rate :: Int
rate = 30

disk :: Float -> Picture
disk radius = ThickCircle (radius / 2) radius

redDisk :: Picture
redDisk = color red (disk 25)

type Position = (Float, Float)
type Velocity = (Float, Float)
type State = (Position, Velocity)

initialState :: State
initialState = ((-200, 100), (60, 0))

displayFunc :: State -> Picture
displayFunc ((x, y), _) = Translate x y redDisk

updateFunc :: Float -> State -> State
updateFunc dt ((x, y), (vx, vy))
    = ((x + vx * dt, y + vy * dt)
      ,(         vx, vy - 9.8 * dt))

simulateProjectile :: IO ()
simulateProjectile = simulate displayMode black rate initialState displayFunc
                     (\_ -> updateFunc)

実行結果

やたらと落下が遅く感じるのは、1 pixel = 1 m の単位になっているせい。この例では半径 25 m の球が初速 \bm{v} = (v_x, v_y) = (60, 0)\;[\mathrm{m/s}] で自由落下していっている。

脚注

  1. https://hackage.haskell.org/package/gloss-1.13.2.2/docs/Graphics-Gloss.html#v:simulate ↩︎