🕴

TypeScript における型の集合性と階層性

2022/08/04に公開

TypeScript

型システム

tech

宣伝 (本を作成しました)

この記事についての発展的研究内容を以下の本としてまとめました。この記事を読んで興味が湧いたら、ぜひ読んでみてください。

はじめに

前回の記事では TypeScript における型の拡大 (Widening) について解説しました。Narrowing の記事を書く前に (Widening を深く理解するためにも) 必要な知識や考え方がいくつかあると思ったので、今回は型の集合性と階層性について見ていきたいと思います (~~短いですが~~内容的に切り出してもかなり興味深いので)。

この記事の最後で別の型の変数同士で代入できるかどうかを示す「Assignability (代入可能性あるいは割当可能性)」について解説しますが、集合と階層の概念で考えることで見通しが非常によくなり、型一般についてもスッキリと理解できることが多くなります。また、never や unknown といったいまいち分かりづらい型についても、なぜ存在しているのか、どういった位置にあるのかが理解しやすくなります。

ChangeLog

大きな変更のみトラッキングしています。

2023-10-15
- any 型を特別扱いして部分型の図を整理
- Lattice の話などを追加
- 圏論の話や双変性についての話を追加
2023-09-24
- 推移性についての記述を修正
- 関数型の部分型関係の説明を追加
2023-09-23
- 構造を整理
- ３つのオブジェクト型についての情報を修正
2023-09-19
- 全体的に内容更新
- 推移性と順序集合についての記述を追加
- Scala の型階層についての記述を追加
- TypeScript の型階層図を修正
- 推移性が成り立たないケースについての記述を追加
2023-02-27
- 関数の型についての情報を記載
2023-02-24
- いくつかの内容について修正
2022-08-30
- 見出し構成を変更
- extends についての記述を追加

型の集合性

Collective type と Unit type

前回記事で解説した "Literal Widening" は "text" や 42、true などのリテラルから作られるリテラル型は、変数が mutable になる場所では string 型といった一般的な型に拡大されて型推論されるという話でした。

const strConst = "text";
//    ^^^^^^^^: "text" 文字列リテラル型として型推論される
let strLet = "text";
//  ^^^^^: string 型として拡大されて型推論される

let mutable = strConst;
//  ^^^^^^^: string 型として拡大される

実は "text" や 42、true といった具体的なリテラルの値から作られるリテラル型に対して、通常はプリミティブ型 (Primitive type) と呼ばれる string や number、boolean といった一般的な型は 集合型 (Collective type) と呼ばれることがあります。

現時点最新の公式ドキュメントには記載されていませんが、古いバージョンでは Collective type について言及されています。あるいは Playground の Literals のサンプルにも記載されています。

A literal is a more concrete sub-type of a collective type. What this means is that "Hello World" is a string, but a string is not "Hello World" inside the type system.
(TypeScript: Handbook - Literal Types より引用)

リテラル型は集合型の具体的な Subtype である旨が記載されていますね。

ちなみに Subtype(部分型、派生型、下位型) とは型の親子関係のようなもので、ある型の下位の型、つまり子の型として定義されたものを Subtype と呼びます。Subtype の派生元、つまり親の型となるものは Supertype(基本型、上位型) と呼ばれます。

２つの型の関係を簡易的に判別するには、受け入れる値の範囲が広く型の制約 (条件) が緩いものが Supertype で、受け入れる値の範囲が狭く型の制約がより厳しいものが Subtype です。もちろん、Supertype と Subtype の関係性にない場合もありえます (number と string を比較した場合など)。

TypeScript で採用されているこういった型の仕組みは「部分型 (Subtyping)」と呼ばれるものであり、より具体的には「構造的部分型 (Structural subtyping system)」というシステムです。このシステムを採用しているのは Go、Scala、OCaml などの言語です。

Subtyping の概念自体は、1960 年代までさかのぼり、Simula というプログラミング言語によって初めて導入され、その概念が脚光を浴びたのはオブジェクト指向プログラミング (OOP: Object-Oriented Programming) でそれが主流になったためであるとのことです。

The notion of subtyping in programming languages dates back to the 1960s; it was introduced in Simula derivatives. The first formal treatments of subtyping were given by John C. Reynolds in 1980 who used category theory to formalize implicit conversions, and Luca Cardelli (1985).
(Subtyping - Wikipedia より引用)

ややこしいことに OOP の文脈では、型 (interface) 同士の関係を指す Subtyping による継承と、既存のオブジェクトから新しいオブジェクトを作成するための言語機能から来る実装間の継承があります。Inheritance (継承) というときにはこの２つの異なる概念があることに注意してください。

Subtyping: Interface inheritance
Inheritance: Implementation inheritance

実際にインターフェース型を継承させて Subtype を作り出すことができます。

interface Animal {
  name: string;
  age: number;
}

interface Dog extends Animal {
  bread: string;
  bark(): void;
}

const myDog: Dog = {
  name: "John",
  age: 2,
  bread: "Labrador Retriever",
  bark: () => console.log("Woof"),
}

const myAnimal: Animal = myDog;

実際、型は値の集合 (より厳密に言えば値と利用できる操作の集合) であり、具体的な文字列の値はすべての文字列を集めた string 型の要素として考えることができます。逆に、具体的な文字列リテラルによってつくられる一つの文字列リテラル型は string 型という集合の部分集合 (Subset) としてみなせます (一つの具体的な値からそれに対応するリテラル型という単集合ができる)。

Type 型とは：型とは、値の集合であり、その集合に対して実行できることの集合である。
少しわかりにくいと思うのでいくつか例を示しましょう。

boolean type は、全ての boolean 値（といっても二つしかないが。true と false の二つである）の集合であり、この集合に対して実行できる操作の集合である。

number type は全ての数値の集合であり、この集合に対して実行できる操作の集合である (例えば +, -, *, /, %, ||, &&, ?) である。これらの集合に対して実行できる操作には、.toFixed, .toPrecision, .toString といったものも含まれる。

string type は全ての文字列の集合であり、それに対して事項できる操作の集合である。(例えば + , || , や && ) .concat や .toUpperCase などが含まれる。

(合法 TypeScript 第3章 Type の全てより引用)

そして、集合型 (Collection type) に対して、単位型 (Unit type) という概念もあることが数値リテラル型などのプルリクエストで言及されています。

All literal types as well as the null and undefined types are considered unit types. A unit type is a type that has only a single value.
(Number, enum, and boolean literal types by ahejlsberg · Pull Request #9407 · microsoft/TypeScript より引用、太字は筆者強調)

単位型 (Unit type) は、単一の値のみを持つ型 であり、すべてのリテラル型は null 型や undefined 型と同じく単位型であると見なされるとのことです。

https://en.wikipedia.org/wiki/Unit_type

string 型は単位型である文字列リテラル型の集合型であり、各文字列リテラル型は string 型の Subtype ということです。これは他のリテラル型とその型を Widening した集合型にも言えます。実際、boolean 型は true と false という真偽値リテラル型のユニオン型、つまり true | false という型と等しいことも明言されています。

The predefined boolean type is now equivalent to the union type true | false.
(Number, enum, and boolean literal types by ahejlsberg · Pull Request #9407 · microsoft/TypeScript より引用)

あるいは Handbook の『TypeScript for Functional Programmers』の項目にも記載されていました。

Unit types are subtypes of primitive types that contain exactly one primitive value. For example, the string "foo" has the type "foo".
(中略)
When needed, the compiler widens — converts to a supertype — the unit type to the primitive type, such as "foo" to string. This happens when using mutability, which can hamper some uses of mutable variables:
(TypeScript: Documentation - TypeScript for Functional Programmers より引用)

Unit type は単一のプリミティブ値を持つプリミティブ型の Subtype であり、文字列リテラル型 "foo" は string 型の Subtype である旨が記載されていますね。そして、mutable な場所で Widening が起きるときには Subtype から派生元の Supertype へと変換されるとも書いてあります。

Types as Sets

Unit type の集合が Collective type(具体的には string などのプリミティブ型) であったわけですが、型が具体的な値の集合である (と考えた方が良い) ということは、公式ドキュメントの『TypeScript for Java/C# Programmers』のページの『Types as Sets』の項目で明言されています。

In TypeScript, it’s better to think of a type as a set of values that share something in common. Because types are just sets, a particular value can belong to many sets at the same time.
(TypeScript: Documentation - TypeScript for Java/C# Programmers より引用、太字は筆者強調)

(可能な操作や演算などの体系などが) 共通している値の集合が型であり、それぞれの値は複数の集合 (型) に属すことができることが言及されていますね。

TypeScript ではこのように型を集合として考えることで直感的に理解することができるとも記載されています。

TypeScript provides a number of mechanisms to work with types in a set-theoretic way, and you’ll find them more intuitive if you think of types as sets.
(TypeScript: Documentation - TypeScript for Java/C# Programmers より引用、太字は筆者強調)

TypeScript 自体は型を集合論的に扱える仕組みを提供するようにデザインされているわけです。実際、ある値が特定の型の変数に代入可能であるかどうかは、その集合 (型の範疇) に属しているかで決まります。

そして、型が集合であること (あるいはそのように扱えること) は、Microsoft Developers の以下の動画にて TypeScript の開発者である Anders Hejlsberg 氏 (この記事や前の記事で参照しているプルリクエストは大体この方の作成) が直々に説明していました (26:32~あたりから)。

実際に型が集合であることを説明するために、この公演の解説を参考に図を作成してみました。

まず、型は各リテラル値によって作られるリテラル型 (Unit type) によって構成されています。これが集合の元となります。null 型や undefined 型も単一の値によって作られるので Unit type です。そして同じ種類のリテラル型の集合が Collective type たる string 型や number 型を構成します。

集合の元

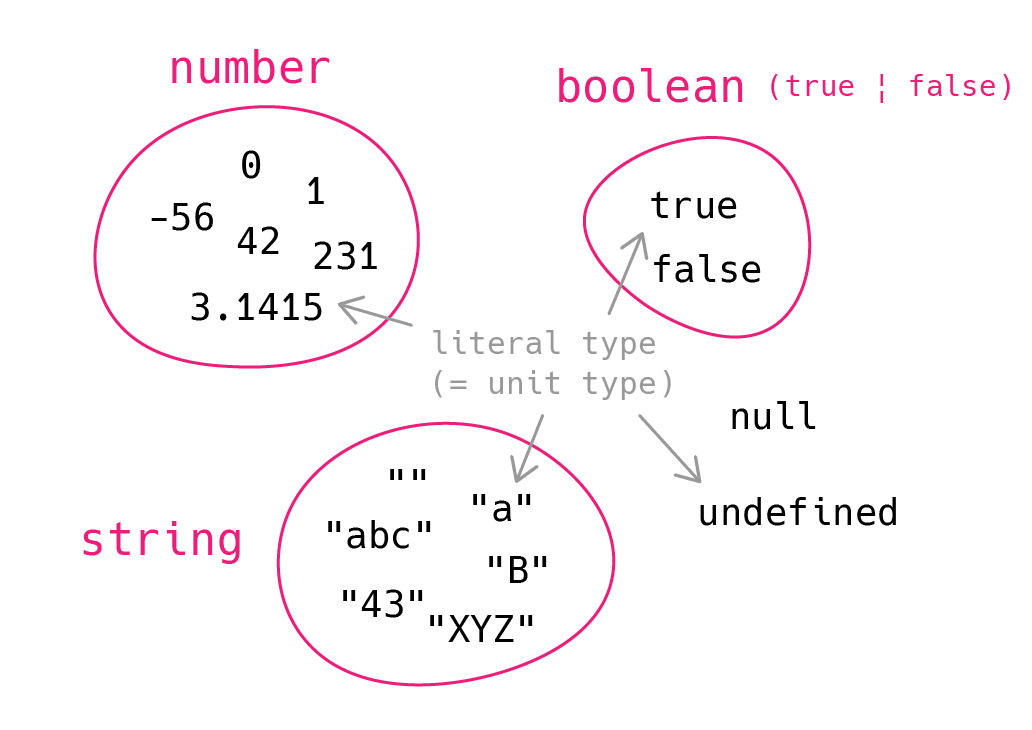
string や number は無限に要素があるから分かりにくいですが (number 型の要素は実際には有限で表現可能範囲に限界がある)、 boolean 型は true と false というたった２つのリテラル型から構成されたユニオン型なので集合が非常に分かりやすいですね。

boolean 型がそうであるように、ユニオン型によって型の和集合を作成できます。例えば 0 | 1 | true | "a" のような数値リテラル型と真偽値リテラル型と文字列リテラル型によるユニオン型は以下のような集合を作成します。

和集合

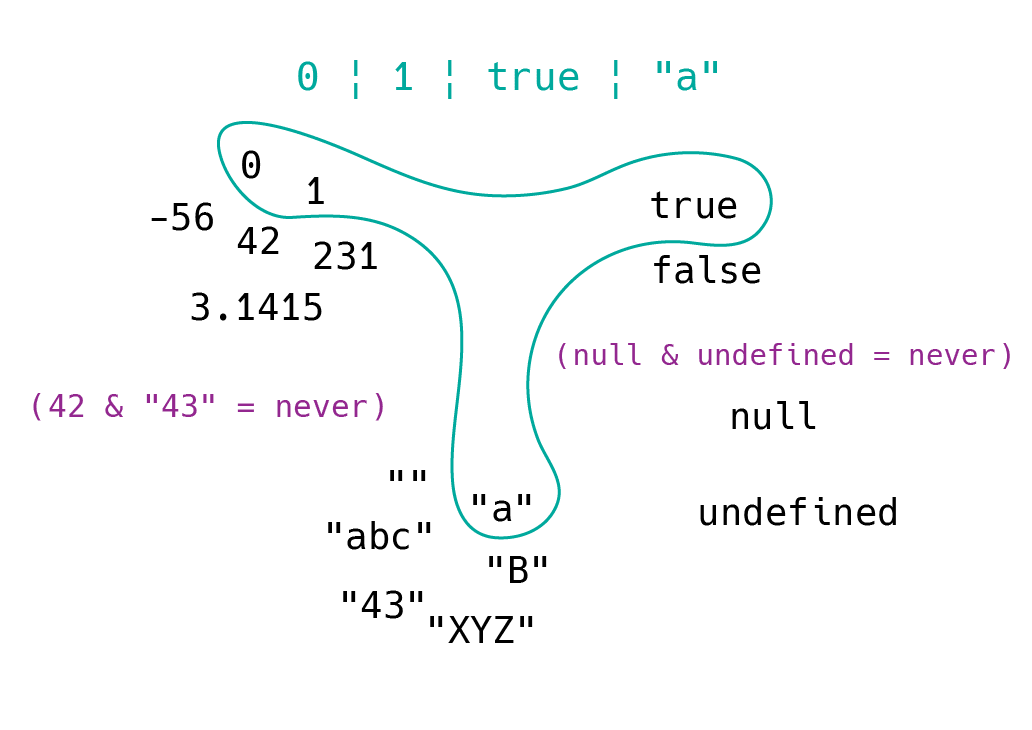
number | string | undefined のようにいくつかの Collective type や Unit type の和集合を作ることもできます。

集合型の和集合

空集合 (Empty set) となる値を持たない型は never 型であり、各リテラル型の交差や異なる集合型の交差をインターセクション型で作ろうとすると never 型となります。図にあるように number & string という異なるプリミティブ型同士のインターセクションによる交差は共通部部分が存在しないため、型の合成結果として never 型が返ってきます。ちなみに空の交差が never 型になるというこの機能は以下の PR で実装されました。

そして型の全体集合 (Universal set) は unknown 型となります。

全体集合

和集合 (Union type) と交差 (Intersection type) についてはオブジェクトの型で考えると分かりやすいです。{ a: "st" } という型と { b: 42 } という型について考えたときのユニオン型とインターセクション型を図示すると以下のような分かりやすいベン図になります。

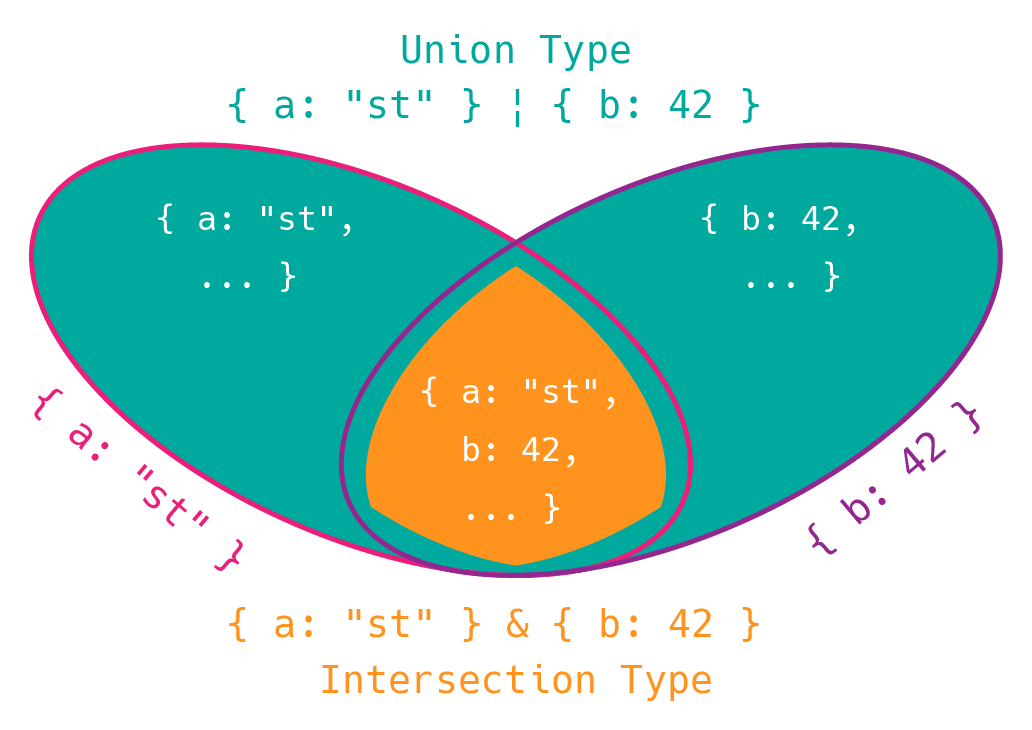
オブジェクトの型

図にあるように、{ a: "st" } 型は a というプロパティの値の型が文字列リテラル型 "st" であるという 条件を満たしたあらゆるオブジェクトの集合 を表し、{ b: 42 } 型は b というプロパティの値の型が数値リテラル型 42 であるという 条件を満たしたあらゆるオブジェクトの集合 を表します。

そして、{ a: "st" } 型と { b: 42 } 型の和集合 (Union type) と交差 (Intersection type) が上の図のようになるのは実際にコードを書くことで分かります。ユニオン型が和集合なのでそれぞれの集合の要素を受け入れますが、インターセクション型は共通要素のみしか受け入れません。

type A = { a: "st" };
type B = { b: 42 };

type Union = A | B;
type Intersection = A & B;

const v_AOrB1: Union = { a: "st" };
const v_AOrB2: Union = { b: 42 };
const v_AOrB3: Union = { a: "st", b: 42 };

const v_AandB: Intersection = { a: "st", b: 42 };

// インターセクション型はユニオン型に含まれる部分集合なので代入可能
const v_AOrB: Union = v_AandB;

型システム一般においてもインターセクション型 (Intersection type) は $\sigma\cap\tau$ として、ユニオン型 (Union type) は $\sigma\cup\tau$ として表記されます。集合の積と和の表現と同じですね。

型システムでの表記 Type system - Wikipedia より引用

ちなみに { a: "st" } という型が { a: "st"; c: number } など任意の他のプロパティを持つあらゆるオブジェクト (あるいはオブジェクトリテラル型) の集合であることは図で考えれば直感的に分かりやすいのですが、実際にコードで書こうとするとエラーがでてしまうので違うのではないかと疑問に思ってしまうことがあります。

type A = { a: "st" };

// A 型は a 以外のプロパティを持つオブジェクトを受け入れない?
const vA: A = { a: "st", c: "anything" };
//                       ^^^^^^^^^^^^^: [Error]
// Object literal may only specify known properties, and 'c' does not exist in type 'A'.

実はこれは型システムにおける違反検知の型チェックエラーではなくて、余剰プロパティチェック (excess property checks) という別のエラーです。TypeScript の型システム的には問題なくても、エラーとして検知してくれるものです。型システム上は問題ないので、別の変数を経由させることでエラーとならなくなります。

type A = { a: "st" };

const obj = { a: "st" as const, c: "anything" };
const vA: A = obj; // エラーとならないで受け入れられる

ということで、{ a: "st" } という型は { a: "st"; c: number; d: string } など a: "st" 以外の任意のプロパティを持つオブジェクト (あるいはオブジェクトリテラル型) の集合であることが分かります。

このことからも上図だとインターセクション型として表現されている { a: "st"; b: 42 } という型はより制約 (条件) が緩い { a: st } 型や { b: 42 } 型の部分集合であることが分かります。

type A = { a: "st" };
type B = { b: 42 };
type AB = { a: "st"; b: 42 }; // A & B (A と B の条件を満たす)

const ab: AB = { a: "st", b: 42 };
const a: A = ab; // A という型の範疇
const b: B = ab; // B という型の範疇

実際にこのような代入が可能なのは、TypeScript が構造的部分型(Structural Type System) というシステムを採用しているからです。

オブジェクト型のユニオンやインターセクションを見ればわかるように、合成などの型操作は集合の領域に対しての操作と同じことになります。オブジェクト型でなくても例えば string | number と string | boolean という２つのユニオン型を合成すれば、交差 (インターセクション) は string 型となり、和集合 (ユニオン) は string | number | boolean 型となります。

余剰プロパティチェックについては uhyo さんの以下の記事で非常に分かりやすく解説されていたので参考にしてください。ユニオン型が OR 演算によって生成されるということについても解説されています。

extends での判別

話は少し変わりますが、extends キーワードでの型の集合性について考えてみたいと思います。

extends はインタフェース型の継承に利用するキーワードで、構造的部分型においてプロパティが増えるたびに継承元に対して Subtype となっていくことがわかりやすいでしょう。

interface Animal {
  name: string;
}

interface Duck extends Animal {
  sound: string
}
// { name: string; sound: string; }

interface Donald extends Duck {
  color: string;
}
// { name: string; sound: string; color: string; }

const don: Donald = {
  name: "ドナルド",
  sound: "guwa",
  color: "blue",
};
const duc: Duck = don;
const ani: Animal = duc;

Donald は Duck の Subtype であり、Duck は Animal の Subtype です。

extends の基本が分かったところで、少し応用的な話に移ります。

ユーティリティ型である Exclude<UnionType, ExcludedMembers> 型などを自分で実装すると理解できるのですが、extends キーワードを使った条件型 (Conditional type) は型変数がユニオン型だと分配法則によって条件判定をユニオン型を構成する各要素に対してイテレーションします。この機能は分配条件型(Distributive Conditional Types)と呼ばれています。条件の判断を型の要素それぞれに分配して新しい型を作成するわけです。

type MyExclude<T, U> = T extends U ? never : T;

type Test = MyExclude<1 | 2 | 3, 2>;
// = 1 | 3

/* イテレーション
T extends U ? never : T
-----------------------
1 extends 2 =>(false) 1
2 extends 2 =>(true) never
*/
// MyExclude<1,2> | MyExclude<2,2>
// 1 | never => 1

参考:
- Exclude<UnionType, ExcludedMembers> | TypeScript: Documentation
- Distributive Conditional Types | TypeScript: Documentation

次のように U もユニオン型になった場合はどうでしょうか？

type Uni1 = 1 | 2 | 3 | 4;
type Uni2 = 1 | 3;
type Test2 = MyExclude<Uni1, Uni2>;
//             1|2|3|4 ^^^^  ^^^^ 1|3
// = 2 | 4

/* イテレーション
T extends U ? never : T
-----------------------
1 extends 1|3 => ???
2 extends 1|3 => ???
3 extends 1|3 => ???
4 extends 1|3 => ???
*/

T extends U では型パラメータ T を U という型パラメータで制約をかけるので、U が Supertype で T が Subtype となるか、あるいは T が U そのものとなります。この制約は T 型が U 型の条件を満たせばよいだけです。

プリミティブ型だと分かりづらいですが、オブジェクト型だと extends で型を制約 (constrain) することが分かりやすくなります。extends キーワードによる型パラメータの制約は条件型以外にもジェネリック型やジェネリック関数などでも利用できるので、次のように型パラメータ Type を { length: number } というプロパティを持つオブジェクトの型で制約すると、その制約条件を満たす値しか引数として受け付けません。制約を設けずに Type だけにしてしまうと型の範囲が広すぎて引数に渡す変数が length プロパティを持つことを保証できませんが、逆に制約を設けることで関数内の変数が length プロパティを持つことを保証できます。

// 制約条件 { length: number } を満たす値のみを引数として受け取る(満たさなければ型エラー)
function longer<Type extends { length: number }> (
  a: Type,
  b: Type
): Type {
  if (a.length > b.length) {
    // length プロパティを持っていることが保証されている
    return a;
  } else {
    return b;
  }
};

length プロパティは少し特殊で、文字列や配列などの値はこのプロパティをもともと持っており引数として渡すことができるので、以下のようなコードが有効となります。

longer("st", "str"); // 文字列は length プロパティを持つ
// => "str"
longer([1, 2], [1, 2, 3]); // 配列は length プロパティを持つ
// => [1, 2, 3]
longer({ length: 42 }, { length: 53, name: "obj" });
// => { length: 53, name: "obj" }

話を条件型に戻すと、extends での条件部がユニオン型に関するものだと true になるか false になるかは一見分かりづらいですが、集合で考えることでスッキリと理解できます。Subtype は Supertype の部分集合です。特にユニオン型では、それを構成する各メンバーはユニオン型自体の部分集合 (subset) となります。

typeSet_6

1 | 3 というユニオン型は 1 と 3 という２つの数値リテラル型の和集合です。従って、1 という数値リテラル型はこの和集合に含まれるため、1 extends 1 | 3 は true であり、条件型からは never 型が返されます。

1 | 3 のユニオン型の集合には 2 や 4 といった数値リテラル型は含まれないため、2 extends 1 | 3 と 4 extends 1 | 3 の条件判定は false となりそれぞれで 2 と 4 という数値リテラル型が返されます。

表にまとめると次のようになります。

条件部	判定	返却される型
1 extends 1 \| 3	true	never
2 extends 1 \| 3	false	2
3 extends 1 \| 3	true	never
4 extends 1 \| 3	false	4

ということで、MyExclude<Uni1, Uni2> で最終的に返される型はイテレーション結果を合成したユニオン型となるので、never | 2 | never | 4 つまり 2 | 4 というユニオン型が返されます。

単純なジェネリクスの利用時に型引数そのものに extends キーワードで制約をかける際にも集合で考えると、制約元の型集合内で条件を満たす部分集合であると理解できます (条件を満たしていれば良いので、制約元の型そのものでもよいです)。

この extends による型パラメータの制約機能は TypeScript 1.8 で導入された機能であり、型理論では一般に F- 有界量化 (F-bounded quantification) と呼ばれる類のものだそうです。

有界量化 (Bounded quantification) 自体は Wikipedia だと以下のような概念として解説されています。公式 Handbook でも Wikipedia の記事自体が言及されているので基本的にはあっているはずです。

In type theory, bounded quantification (also bounded polymorphism or constrained genericity) refers to universal or existential quantifiers which are restricted ("bounded") to range only over the subtypes of a particular type. Bounded quantification is an interaction of parametric polymorphism with subtyping.
(Bounded quantification - Wikipedia より引用、太字は筆者強調)

専門用語が多すぎるので分かりづらいですが、簡易的に意訳すると特定の型の Subtype の領域にのみ制限する記法のことです (間違ってたらすみません)。これでジェネリクスとサブタイピングの相互作用を表現します。

考え方としては、考慮すべき型の領域として境界 (boundary) を設けることでジェネリクスなどでの型パラメータがとり得る型 (値) の範囲を制限して使いやすくしているだけです。そして型が値の集合であることを知っていると、境界内の領域はすなわち集合の領域そのものとなります。T extends U という条件を図で表現すると次のような感じです。

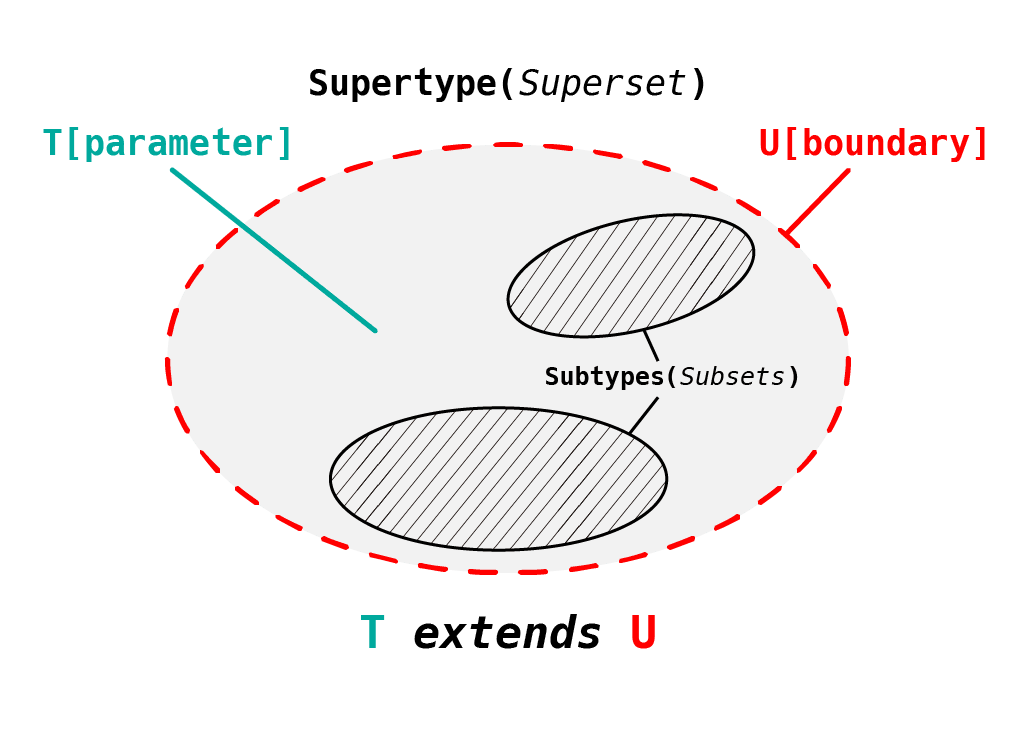
img_typeSet_7

型パラメータ T は境界 (制約) を規定する U 型の領域内のあらゆる範囲を動くことができ、その範囲であればどのような Subtype でも良いわけです (もちろん U そのものでもよい)。１つの Supertype に対して Subtype は複数ありえるので上のような図となります。

図では U も型パラメータにしていますが、例えば unknown[] などをいれて T extends unknown[] というように配列型などの具体的な型で拘束して考えてみると良いでしょう。

関数の型

型は具体的な値の集合であると述べましたが、型を集合として捉える時、具体的な関数も型の要素となります。そもそも関数はオブジェクトであり値ですから、関数の型も具体的な関数実装の集合であるわけです。

TypeScript では以下のように関数の型を定義できます。

// 関数の型を定義
type NumberOp = (num: number) => number;

// 関数の型で注釈して具体的な関数を実装する
const increment: NumberOp = (param) => {
  //                         ^^^^^^ number 型の引数
  return param + 1;
  //     ^^^^^^^^^ number 型の返り値
};

console.log(increment(42)); // => 43

上記コードで定義した具体的な関数 increment は関数の型である NumberOp という集合内の 1 つの要素となります。NumberOp 型、つまり (num: number) => number という関数型の集合には他にも以下のような具体的な関数の要素が含まれています。

// (num: number) => number 型の関数値
const double: NumberOp = (param) => {
  return param * 2;
};

// (num: number) => number 型の関数値
const sqrt: NumberOp = (param) => {
  return Math.sqrt(param);
};

このようにある関数の型定義を満たすような具体的な関数の実装がその関数型の集合についての要素となります。

ただし、プリミティブ型やオブジェクト型の値 (value) のように関数の型を集合として捉えて、型の合成やサブタイプ互換性について考えるにはいくつか難しいことがあるので、素朴な集合論よりも対象 (object) と射 (arrow) を扱う圏論の方が適しているかもしれません。

また、関数の型はシグネチャ (引数の数、引数の型、返り値の型) について考慮しなくてはなりません。このときにそれぞれの要素についてサブタイプ互換性の変性 (variance) という概念も必要になります。特に関数の型は引数の型については双変 (bivariant) あるいは反変 (contravariant) になります。

長くなるのであまり詳細には解説しませんが(詳細について公式ドキュメントを参照してください)、関数型 S1 -> S2 と T1 -> T2 があったときに入力の値の型について T1 <: S1 (T1 が S1 の部分型) であり、かつ出力の値の型について S2 <: T2 (S2 が T2 の部分型) になっているとき関数型 T1 -> T2 が期待される場所で S1 -> S2 で安全に置換できるといい、このとき S1 -> S2 は T1 -> T2 の Subtype である、ということになります。

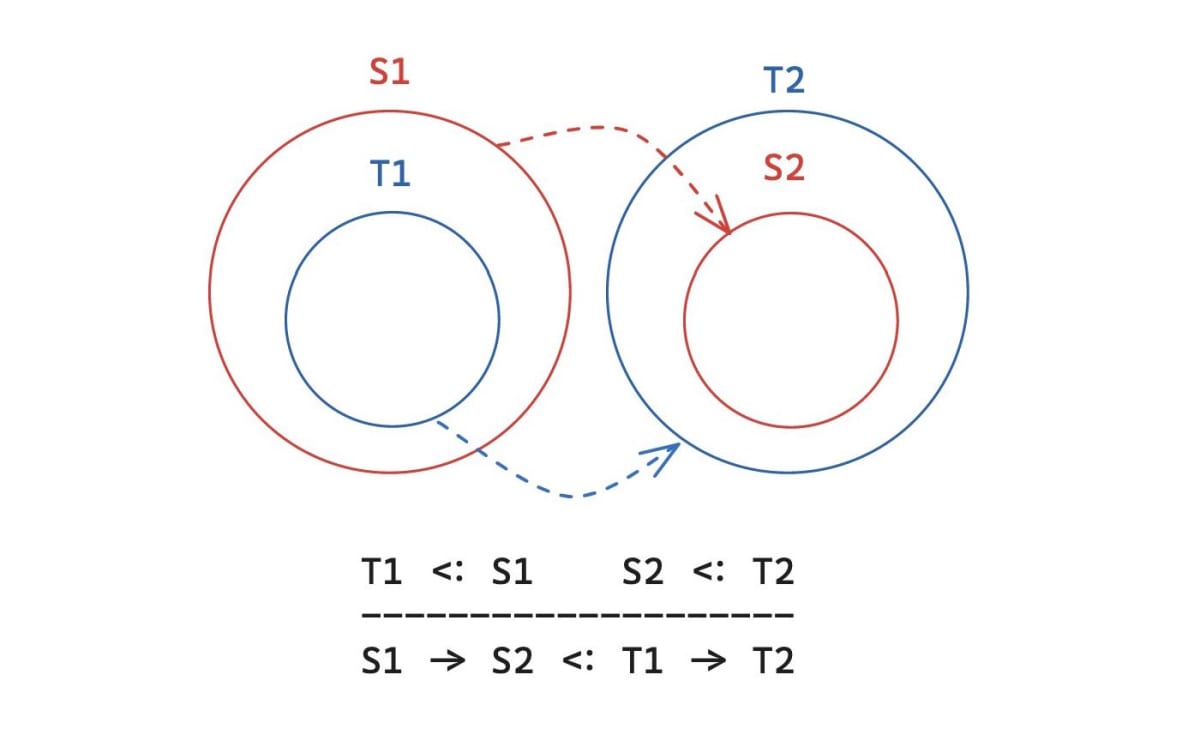
関数型の入力と出力の包含関係

これまでの単純な型同士の包含関係が部分型関係となっていたのとは異なり、直感的な理解は少し難しくなっています。実は部分型関係というのはそもそもが型の互換性(期待される型に対して安全に置換できるかどうか)という関係なので実際には包含関係とは異なるものとなっています。そのため関数型では実際の部分型関係の本質的な理解が必要となります。

関数型の部分型関係は直感的に集合の包含関係で理解するのは少しむずかしいですが、集合論的な考えをもったまま関数について以下の図の(2)のように入口と出口があるパイプの管を置き換えるようなイメージで考えると理解できます。パイプの入口と出口はそれぞれ集合を表現する領域の大きさを持つとして考えてください。

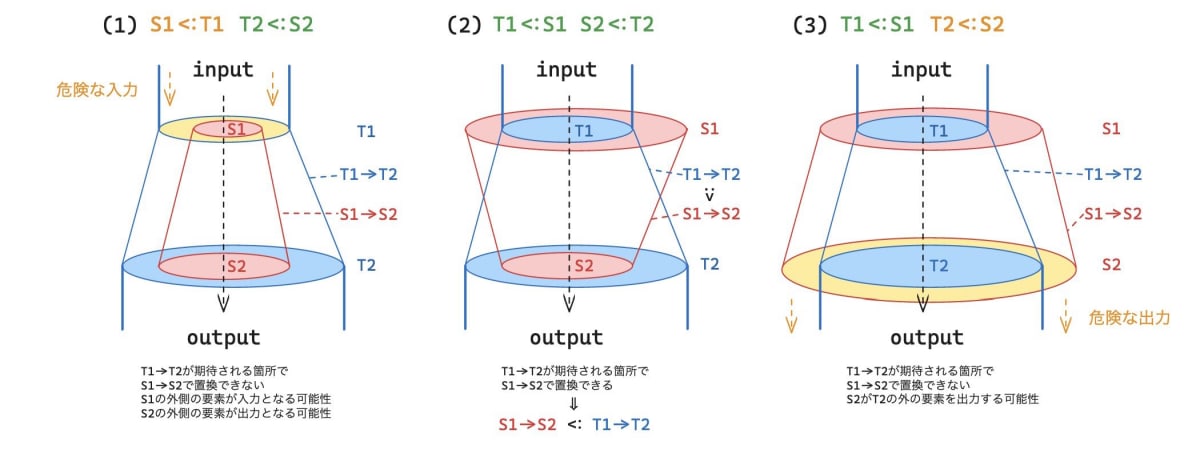
関数型の部分型関係

T1 -> T2 という関数型を図のような T1 という領域の大きさを持つ入力口と T2 という領域の大きさを持つ出力口のある水が流れるパイプとして考えてください。T1 の面積を流れてくる入力をパイプ外にこぼさず、かつ T2 の面積を流れてくる出力をパイプ外にこぼさないように別のパイプ(S1 -> S2)で安全に置き換えるとします。

図の(1)では入力口である S1 の面積が元の入力口の T1 よりも小さいため入力となる水がこぼれて危険であり、(3)では逆に出力口である S2 の面積が元の出力口の T2 よりも小さいため出力となる水がこぼれて危険な置換となります。

一方、図の(2)では元の入力口の T1 よりも大きな面積をもつ S1 で入力となる水を受け取り、元の出力口の T2 よりも小さな面積を持つ S2 で出力となる水を吐き出します。これによって上下で繋がっているパイプの外側に水がこぼれることなく安全にパイプの入れ替えができることがわかります。

このように入力と出力の値の範囲の外側となるような危険な入出力をとらない関数であれば元の関数が期待されるような場所で使用しても大丈夫というわけです。

これが関数の型における部分型についての基本的な関係です。現実的には TypeScript の関数型では利便性のために関数の引数については双変(bivariant)となるように設計されています。引数として受け取る関数の型がより特殊化されたものとして受け取れるほうが便利なケースが多いためです。つまり上図の(1)のようなパターンを認めています。

型の階層性

Top type と Bottom type

Subtype や Supertype という関係から分かる通り、型には親と子のような関係があり、これをたどることで階層性が見えてきます。これは集合性について見方を変えるだけですが階層性で考える方が都合のよい場合があります。すべての型の最上位となる親の型は TypeScript では unknown 型であり、型理論(Type theory) ではこのような型を Top type(トップ型) と呼びます。

https://en.wikipedia.org/wiki/Top_type

逆に最下位となる型は TypeScript では never 型であり、型理論ではこのような型を Bottom type(ボトム型) と呼びます。

実際、公式 Handbook の『TypeScript for Functional Programmers』の項目でも unknown 型が Top type で never 型が Bottom type であると明示されています。

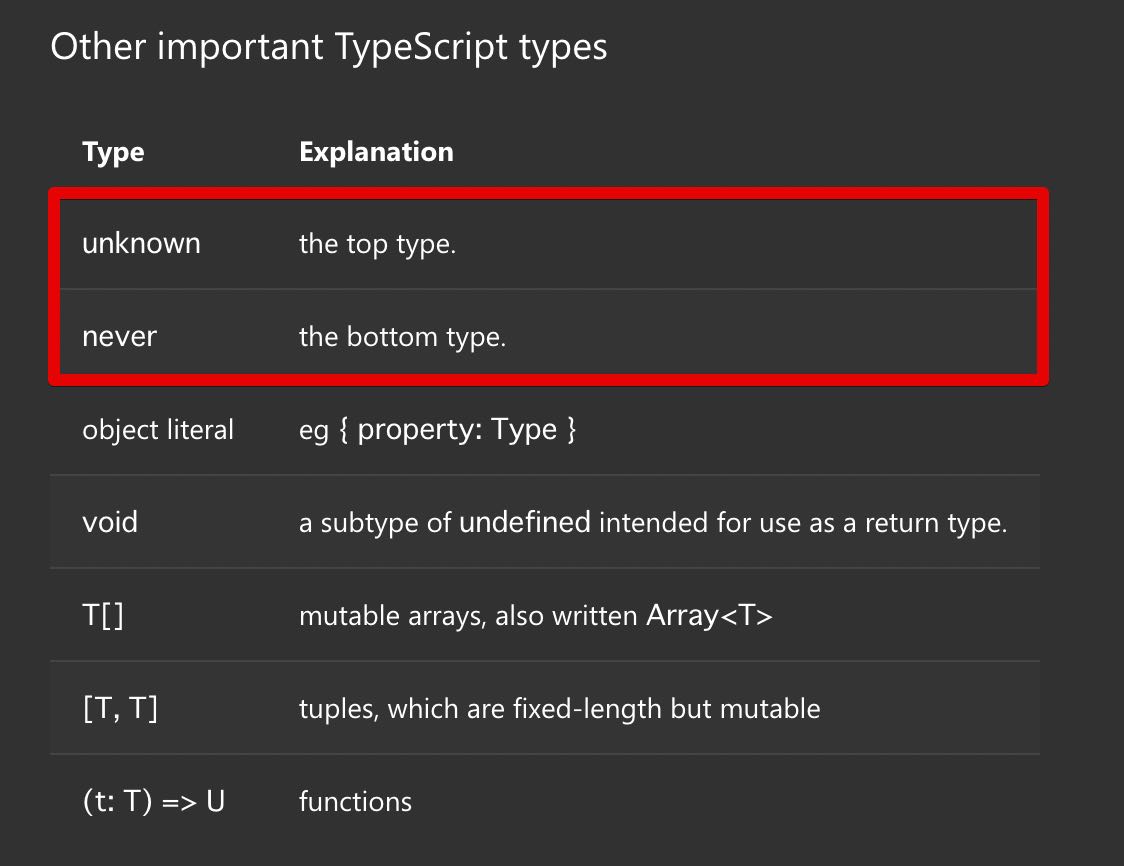unknown & never type TypeScript for Functional Programmers より引用

Top type としての unknown 型自体の実装は以下の PR で行われました。

Bottom type としての never 型自体の実装は以下の PR で行われました。

型の集合性で見たとおり、直感的に型は値の集合なので、TypeScript のリテラル型は単一の値からなる単集合で、never 型は値を持たないので空集合 (Empty set) です。全体集合 (Universal set) を unknown 型としてみなすと以下のような図が書けました。

全体集合

それぞれの型は unknown 型という全体集合の部分集合です。

参考文献

Type hierarchy

Subtype と Supertype の関係を辿ると型の階層 (Type hierarchy) ができあがります。Type hierarchy という言葉は TypeScript の文脈ではなかなか見ない言葉ですが、例えば Scala の公式ドキュメントにでてきます。

Scala ではプリミティブ型が存在せず、あらゆる型が Top type である Any 型 (Any クラス) を継承してサブタイプとなっているため、以下のようなヒエラルキーが形成されており、継承による階層図となっています。

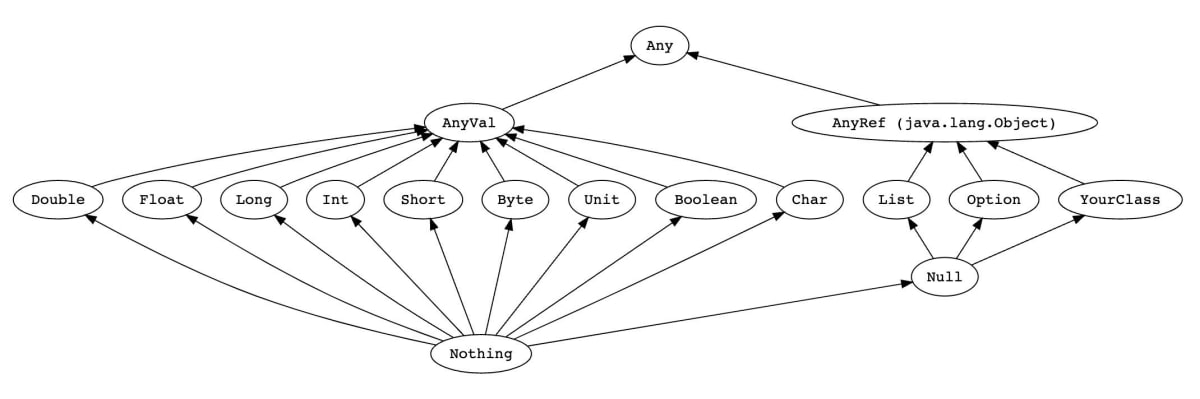ScalaのType hierarchy Scala の Type hierarchy (公式ドキュメントより)

C# や Scala といった言語でのこのような型のシステムを Unified type system と呼ぶそうですが、Java や JavaScript (TypeScript) ではプリミティブ型が存在しているため完全に同じように考えることができません。

図を見てわかるように Scala では TypeScript と同じように Top type と Bottom type が存在しており、階層図の最上位と最下位に位置している Any 型と Nothing 型が Top type と Bottom type となります。Any 型は TypeScript の Object 型と同じように toString() などのあらゆるオブジェクトで利用できるメソッドなどを定義しています。

Scala と JavaScript の機能的な違いについては以下のドキュメントを参照してください。

自動ボックス化とラッパーオブジェクト型

JavaScript (TypeScript) ではプリミティブ型のデータに対して "str".length のようにプロパティアクセスを行ったり、"str".toUpperCase() のようにメソッド呼び出しを行うことができますが、この際には string 型というプリミティブ型の値から String というオブジェクトラッパーへの値に暗黙的な変換 (自動ボックス化) が行われています。

// プリミティブ型のデータ
const st = "string";
st.toUpperCase();
// => "STRING"
// 自動ボックス化でString型のオブジェクトに対してメソッド呼び出しを行っている

// 上と同じことが起きている
(new String("string")).toUpperCase();
// => "STRING"

JavaScript のラッパーオブジェクトに対応して TypeScript にはそのラッパーオブジェクトの型が用意されています。

プリミティブ型	ラッパーオブジェクト型
`string`	`String`
`number`	`Number`
`boolean`	`Boolean`
`symbol`	`Symbol`
`bigint`	`BigInt`
`null`	なし
`undefined`	なし

JavaScript では string 型などのプリミティブ型の値に対してメソッド呼び出しなどが可能ため、すべてのデータがオブジェクト型のように見えてしまいますが、プリミティブ型とラッパーオブジェクトの型での変換プロセスがあるためそのように見えるだけで Scala とは異なる型のシステムであることがわかります。とはいっても、部分型関係の推移性に基づく階層図は同じように作成することが可能です。

部分型関係と順序関係

部分型関係は異なる型同士での親子のような関係でした。より厳密には Subtype である型を Supertype の型が期待される場所で安全に置換できるという関係です。

スーパータイプは、そのサブタイプの数々によって代替/代入可能とされており、これは代入可能性（substitutability）と呼ばれる。そのスーパータイプとサブタイプの関係は、is-a とも言われる。記号 <: を用いて Subtype <: Supertype と表記される。
(サブタイピング (計算機科学) - Wikipedia より引用)

部分型関係は図では is-a-subtype-of という形式で矢印の方向が Supertype になるように表現します。この記事では階層性を表現したいので矢印を逆転させて表現するので注意してください。

部分型関係というのは数学で言うところの二項関係(binary relation) の一種ですが、部分型関係は反射性 (reflexive) と推移性 (transitive) を満たすが、反対称律 (antisymmetic) を満たさないような関係です。

これらの条件は集合論での順序集合 (要素同士に順序関係がある集合) を考える上で必要で、二項関係 ( $\prec$ ) についての以下のような規則です。

(1) 反射律 (reflexive)： $P$ の任意の元 $a$ に対し、 $a \prec a$ が成り立つ。
(2) 推移律 (transitive)： $P$ の元 $a, b, c$ に対し、 $a \prec b$ かつ $b \prec c$ ならば $a \prec c$ が成り立つ。
(3) 反対称律 (antisymmetic)： $P$ の元 $a, b$ に対し、 $a \prec b$ かつ $b \prec a$ ならば $a = b$ が成り立つ。
(4) 完全律 (total)： $P$ の任意の元 $a, b$ に対し、 $a \prec b$ または $b \prec a$ が成り立つ。

例えば実数の集合 $\mathbb{R}$ において大小関係 ( $\leqq$ ) は上記４つのすべてを満たします。したがって、実数の集合は全順序集合 (Totally ordered set) と呼ばれる順序集合となります。

当該の部分型関係 ( $<:$ ) についてですが、反射律 ( $S <: S$ ) と推移律 ( $T <: S$ かつ $S <: U$ なら $T <: U$ ) を満たす関係ですが、反対称律は満たしません。

反対称律は $S <: T$ かつ $T <: S$ なら $S = T$ が成り立つというものなので、一見すると部分型関係で成り立っているように思えますが、これはオブジェクト型のプロパティの順番が関係して成り立たくなる場合があるので満たされません。例えば、type A = { a: string; b: number; } と type B = { b: number; a: string; } という２つの型は実は異なる型なのですが、それぞれ部分型関係なので $A <: B$ かつ $B <:A$ が成り立ちますが、 $A = B$ というわけではありません。このように反対称律を満たさない場合が成立するので部分型関係を持つ型の集合は反射律と推移律を満たす前順序集合 (Preordered set) と言えます。

値の集合を型としてみなしたように、今度は型そのものを要素として考えることで型の集合を考えることができます。型システム入門ではこのような型の見方を「部分集合意味論」という言葉で表現しています。型はユニオン型やインターセクション型などで型と型を合成した型も作成できたわけなので、型の集合全体で元ではなく部分集合となるようなものも一つの型として扱えます。つまり、型の集合全体の部分集合の全体として作られる擬似的なべき集合を考えることですべての型を要素とする集合として捉えることができそうです。

集合性の話で見たように型同士には包含関係がありました。実はべき集合はこの包含関係を順序とする半順序集合 (Partially ordered set) となります。ただし半順序集合は、前順序集合であることを前提に更に反対称律を満たす必要があるため、厳密には型の集合はべき集合ではなさそうですね (擬似的といったのはその部分があるからです)。実際、部分型の機能を持つ型システムにおいて型同士の包含関係 (のようにみえていたもの) の本質は部分型関係です。

部分型関係の推移性

さて、階層の話に戻りますが、部分型関係の推移律 ( $T <: S$ かつ $S <: U$ なら $T <: U$ ) を図示することで Scala でみたような型の階層図をつくることができそうです。Top type を最上位の階層、Bottom type を最下位の階層としてみることで階層構造 (ツリーではないです) が作れます。Unified type system のようなすべてがクラスの継承で行われているわけではないですが、部分型関係の推移性に基づく階層は同じようになります。

以下の図は Mermaid で型階層を記述したものです。ただし、全貌図としては正確ではないと思うので注意してください (複数の文献を参考にして作成してますが、TypeScript のバージョン更新によって古い階層図と変わっているところなどもあるので、大体はこんな感じという程度です)。また、enum などの型は JS に存在しない TS の独自機能なので意図的に排除しており、Promise 型や Iterable 型などの型も省略しています (それらの型は Object 型傘下の Subtype です)。

左が Supertype で、右が Subtype の方向となります。一番左に位置している unknown 型がすべての型の Supertype であり Top type です。逆に一番右に位置している never 型がすべての型の Subtype であり Bottom type です。なお部分型関係をより正確に書こうとするとツリー的な階層図ではなくなるので至る所の関係を省略して図示しています。つまりハッセ図に近いです。例えば Bottom type である never 型については、すべての型から never 型に矢印が必要となり図が汚くなるので省略しています。

そして Subtype の型の変数は Supertype の型の変数へ代入可能です。

Widening(型の拡大) が起きる方向は子から親、つまり Subtype → Supertype の方向であり、代入可能となるのも Subtype → Supertype の方向で、その逆は型エラーとなります。

const literal = "text" as const;
let str: string;
let Str: String;
let Obj: Object;
let unk: unknown;

// Subtype → Supertype の方向で代入していくと型エラーにならない
str = literal; // str が Supertype(string型) で literal が Subtype(文字列リテラル型)
Str = str;
Obj = Str;
unk = an;

階層図の中間を省略して拡大するとこんな感じになっています。この図でも部分型関係を完全に表現するためのさまざまな型同士の矢印が省略されていることに注意してください。

３つのオブジェクト型

オブジェクトの型である Object 型、{} 型、object 型はそれぞれ違いがあります。図では３つの型を同じ階層に置いていますがこれは相互に代入可能、つまり相互に部分型であるためです。

const obj1: object = {};
const emp1: {} = {};
let Obj1: Object;
Obj1 = obj1; // OK
Obj1 = emp1; // OK

const obj2: Object = {};
const Obj2: {} = {};
let emp2: {};
emp2 = obj2; // OK
emp2 = Obj2; // OK

const Obj3: Object = {};
const emp3: {} = {};
let obj3: object;
obj3 = Obj3; // OK
obj3 = emp3; // OK

それぞれに部分型関係について詳細に図示すると以下のように３つとも相互に部分型となっています。

これらの Object 型、{} 型、object 型は通常使うことはほとんど無いと思いますが、明示的にそれらの型で型注釈しようとすると Deno 環境だとリンタールールの１つである "ban-types" に別の型注釈をするように注意されます。

具体的にそれぞれがどんか型かを説明すると、Object 型は null と undefined 以外のすべての値 (通常のプリミティブ型とオブジェクト型に含まれるあらゆる型) が代入可能な型です。Object 型は unknown 型と any 型の Subtype であり、それら以外のすべての型の Supertype です。

let Obj: Object;
Obj = 42; // OK
Obj = "str"; // OK
Obj = { a: 42 }; // OK

Obj = undefined;
// Error: Type 'undefined' is not assignable to type 'Object'.
Obj = null;
// Error: Type 'null' is not assignable to type 'Object'.

なお Object 型で型注釈するとエディタで Deno のリンターによって次のように注意され、なんらかのオブジェクトの型で型付けしたい場合には object 型を代わりに使うか、何かしらの値を意味して型付けしたい場合には unknown 型を代わりに使うようにと言われます。

This type may be different from what you expect it to be
If you want a type meaning "any object", use object instead. Or if you want a type meaning "any value", you probably want unknown instead.

ユーザー定義のオブジェクトリテラル型 (一般的なオブジェクトの型) はこの Object 型の傘下の Subtype であり、interface を使ったユーザー定義の型などもすべて Object 型傘下の Subtype となります。

interface I { prop: string }
const i: I = { prop: "val" };
const obj: object = i;

関数の型も Object 型傘下の Subtype です。より具体的に言えば、Object 型の Subtype であるグローバルインターフェース Function 型傘下の Subtype です。

type FT<T> = (arg: T) => T;
const ft: FT<string> = (arg: string) => arg.toUpperCase();
const fc: Function = ft;
const obj: object = ft;

{} はプロパティを持たないオブジェクトの型です。"ban-types" のリンタールールで注意される文には null と undefined 以外を表現するための型であると記載されています。プロパティを持たないオブジェクトと言っても以下のように "ban-types" のルールで空のオブジェクトを意味したいなら Record<string | number | symbol | never> 型を使うようにと促されます。

{} doesn't mean an empty object, but means any types other than null and undefined
If you want a type that means "empty object", use Record<string | number | symbol, never>

let e: {};
e = undefined;
// Error: Type 'undefined' is not assignable to type '{}'.
e = null;
// Error: Type 'null' is not assignable to type '{}'.

This type is tricky to use so should be avoided if possible
Use Record<string, unknown> instead.

2023-09-20 追記: なお object 型を使わないように警告するリンタールールは以下の PR で除去されました。

３つの型の違いをまとめると以下のようになります。

型	説明
`Object`	`toString()` や `hasOwnProperty()` などのすべてのオブジェクトが持つメソッドの提供元であり、あらゆる値 (プリミティブもオブジェクトも) 代入可能な型です
`{}`	空のオブジェクトを表現する型で `Object` 型と似ているが、コンパイル時に異なる挙動を取り、`Object` が持つメンバーを持たず `null` と `undefined` 以外を表現する型です
`object`	TypeScript 2.2 から導入されたプリミティブではないという否定を表現するような型 (non-primitive type) であり、プリミティブ型の値を代入できません

参考

null 型と undefined 型

話は変わって、null 型と undefined 型についてですが、null と undefined はぞれぞれプリミティブ型の値であり、それぞれの型はプリミティブ型の範疇です。string や number といった他のプリミティブ型とは違ってラッパーオブジェクトやその型は存在しません。

また、単一の値からなる型なので Unit type として見なされます。それぞれの型は階層図にあるように any 型の Subtype です。

そして、--strictNullChecks のオプションを無効化している場合は、変数が mutable となる場所で null 型と undefined 型は Widening(Literal widening ではなく一般の Widening) によって Supertype である any 型へと拡大されます。undefined 型は一階層上の void 型ではなく、その上の any 型へと拡大されます。

const nullConst = null;
//    ^^^^^^^^^: null 型として型推論
const undefinedConst = undefined;
//    ^^^^^^^^^^^^^^: undefined 型として型推論

let nullLet = nullConst;
//  ^^^^^^^: any 型として拡大されて型推論
let undefinedLet = undefinedConst;
//  ^^^^^^^^^^^^: any 型として拡大されて型推論

ただし、--strictNullChecks があろうとなかろうと、Literal Widening と同じ様に mutable な場所で直接値を代入すると any 型として拡大されて型推論されます。

let n = null;
//  ^: any 型として拡大されて型推論される
let u = undefined;
//  ^: any 型として拡大されて型推論される

推移性が成り立たないケース

これまでの型の階層図は部分型関係の推移性に基づいて作成したものですが、TypeScript の部分型関係では推移性が成り立たないようなケースが存在するそうです。

部分型関係はその推論規則から推移性が成り立ちますが、例えばプリミティブ型とプリミティブ型の否定を表現する non-primitive object(object) 型の間の関係では推移律が成り立たないケースが発生します。

以下の図は部分型関係について部分的に詳細にしたものです。図の object 型とプリミティブ型の関係に注目してください。object :> Wrapper :> プリミティブ型 という部分型関係があるため、推移律から object >: プリミティブ型 が成立するはずです。※ この節では矢印の方向を正当な向きに戻しています。

より具体的には、プリミティブ型 (string など) がオブジェクトラッパー型 (String など) の Subtype であり、オブジェクトラッパー型が Object 型 (あるいは {}) の Subtype であるので、それらと相互に置換できる object についても通常は部分型関係が推移的に成り立たないといけなくなります。

つまり、object 型にプリミティブ型 string の値が代入できてしまう可能性があるわけですが、実際にそのようなことは起きず、代入しようとすると型エラーが発生します。

let obj: object;
let str: string = "str";
    obj = str;
//  ^^^ error: Type 'string' is not assignable to type 'object'

$string <: Object$ と $string <: \{\}$ は成り立ちますが、 $string <: object$ は成り立ちません。元々 object はプリミティブ型でないこと表現するために新しく追加された型なので、object に string のようなプリミティブ型の値が代入できたらいけないわけですから、このような推移性が成立しないケースとなるのは本来的な目的からは妥当でしょう。

ただし、上図に表現したように object 型の部分型関係において $Object <: object$ が成立している箇所があるため、この部分型関係を経由すれば object 型にプリミティブ型を代入することが可能となってしまっています。

let pri: string = "st";
let Obj: Object;
let obj: object;

// string → Object → object の部分型関係を経由することで代入可能
Obj = pri; // OK → Object :> string
obj = Obj; // OK → object :> Object

// string → object への直接の代入は禁止されている
obj = pri; // NG → Error: Type 'string' is not assignable to type 'object'

このような部分型関係がなくなれば推移性はより整合性が確保されるはずで、object が入る前の推移性はおそらく以下のようにきれいな状態になっていたと思われます。

なお、enum などの型についても推移性が成り立たなくなるケースがあるらしく、上記のブログ記事でそのようなケースについて解説されていました。このケースはおそらく後述する Assignment 互換性が Subtype 互換性の拡張であることが原因となっていると思われます。

Compatibility

さて、上記の階層図と Handbook の『Type Compatibility』の図を見比べると Subtype → Supertype で代入可能である一方で、Supertype → Subtype で代入できないというのが上の階層図と一致しているので納得できます (ただし、any 型は例外で、strictNullChecks によって null 型と undefined 型の挙動も変動します)。

型の互換性 Type Compatibility より引用

代入可能であることや Subtype の関係性は型の compatibility (互換性) として定められています。assignable (代入可能または割当可能) であることと Subtype であることは近似していますが、微妙に異なるということが Handbook の以下の箇所に記載されています。

So far, we’ve used “compatible”, which is not a term defined in the language spec. In TypeScript, there are two kinds of compatibility: subtype and assignment. These differ only in that assignment extends subtype compatibility with rules to allow assignment to and from any, and to and from enum with corresponding numeric values.
(TypeScript: Documentation - Type Compatibility より引用、太字は筆者強調)

Subtype 互換性を拡張したものが割当 (Assignment) 互換性であり、具体的には、any 型から様々な型に代入できることと any 型に様々な型を代入できるというルールが追加されていることが記載されていますね (enum についての言及は無視しています)。

他にも Handbook には次のようなルールが記載されていますが、上のような階層図で考えれば細かいルールを言葉で覚えなくても理解できます (これらのルールは any 型についてのルールが追加された Subtype-Supertype 関係性の部分的な言い換えにすぎないからです)。

すべての型は自身の型へ代入可能
any 型と unknown 型はそれら自身への代入可能な型は同じだが、unknown 型は any 型の除いて他の型へ代入することはできない
unknown 型と never 型はお互いに逆の関係性となっており、unknown 型にはあらゆる型が代入可能であり any 型を除くあらゆる型に代入できない一方、never 型にはあらゆる型が代入できず、あらゆる型に代入可能である
void 型は any 型や unknown 型、never 型、null 型を除くあらゆる型が・に代入できない
strictNullChecks を無効化すると、null 型と undefined 型は never 型に近似して、大抵の型に代入可能、大抵の型が代入不可能となり、お互いに代入可能となる
strictNullChecks を有効化すると、null 型と undefined 型は void 型のように振る舞い、any 型や unknown 型、never 型そして void 型を除くすべての型が・に代入できない (undefined 型は常に void 型) へ代入できる。

Assignability 互換性は実は条件型の条件判定などで利用されています。つまり、以下のような T extends U での判定は正確には部分型関係の判断でなく、割当可能関係の判断となります。

type A = T extends U ? X : Y;

The type above means when T is assignable to U the type is X, otherwise the type is Y.
(from: docs)

ちなみに Assignability についての基本的な仕組みについての説明はアーカイブされている古いハンドブックの方に記載されているので気になる方はこのドキュメントを見るとよいです。

Assignment 互換性は Subtype 互換性を拡張したものですが、なぜそのようなことをする必要があるのかというと、any 型の特殊性に由来すると考えられます。

any 型

上で述べたように any 型は型チェック自体を放棄(型チェックをオフにする)するので、例外的にすべての型に代入可能であり、自身の Subtype である型にも代入できます (上の代入可能であるかの図でもそうなっていますね)。ただし Bottom type である never 型には never 型以外は何も代入できないので any 型でも代入することはできません。

// any 型は型チェックをOFFにしてすべての型の変数に代入できてしまう
const numAsAny = 42 as any;

const und: undefined = numAsAny;
const str: string = numAsAny;
// ただし Bottom type である never 型には代入できない
const nev: never = numAsAny; // [Error]
// Type 'any' is not assignable to type 'never'

any 型は型理論の文脈では一般的に Dynamic type と呼ばれ ? で表現されます。Dynamic type は漸進的型付け(Gradual type system)というシステムで出てくる型で、静的型付けの世界と動的型付けの世界の境界となる型です。Gradual type のシステムは Subtyping とは関係がない独立したものですが、Subtyping の階層に加えることで両立した型システムを作成可能です。

any 型を部分型関係の階層図に加えると以下のようになります。object 型の関係も修正しておきます。Assignability 互換性を表現するための図に近くなりましたが、any 型の変数はあらゆる型へ割当可能なため、正確に Assignability 互換性を表現しようと思うと any 型に対してすべての型から矢印が必要となります。

any 型は TypeScript の初期から存在しており、unknown 型が入るまでは唯一の Top type としてあつかわれていました。unknown 型は型安全な Top type として TypeScript 3.0 から追加された機能です。つまり、any と unknown はどちらも Top type であり、相互に代入可能です。

never 型

never 型は本来的には「値を持たない」ということを表現する型なので、never 型には never 型しか代入できないということを検証するには型アサーションで never 型としてあげることで可能です。また、never 型は最下層の Subtype つまり Bottom type なので never 型からみればあらゆる型が Supertype となり代入可能です (各リテラル型も Supertype です)。

// 通常 never 型は値を持たないはずだが、型アサーションで never 型にできて、never 型に代入できる
const nev: never = 1 as never;

// never 型はどんな型にも代入できる
const str: string = nev;
const strArray: string[] = nev;
const strLiteral: "text" = nev; // リテラル型にも代入可能
const an: any = nev;
const nev2: never = nev; // never 型(自身)に代入可能

void 型と undefined 型

関数の返り値がないことを表現する void 型ですが、return 文を持たない関数の返り値の型は自動で void 型であると型推論されます。そういった関数から返り値を得ようとして返ってくるのは undefined という値です。この２つも Supertype と Subtype の関係です (階層図を参照)。void 型が Supertype で、undefined 型が Subtype なので、void 型に undefined 型は代入可能です (逆はできない)。

const u: undefined = undefined;
const v: void = u;

このような代入関係から明らかに void 型が Supertype であり、undefined 型が Subtype なのですが、Handbook の『TypeScript for Functional Programmers』の項目では void 型の説明が "a subtype of undefined intended for use as a return type." となっています。ただし、アーカイブされた古い仕様を見ると void 型は undefined 型の Supertype として明記してあるのでこれは現在の公式ドキュメントのミスだと思われます。おそらくミスだろうということでプルリクエストを作成しました (バージョン更新によって Supertype と Subtype が入れ替わってしまうような仕様変更は流石にないと思います)。

どうやら別の PR で Subtype の記述自体が削除されたようです。

参考

型の集合性についての参考文献

型の階層性についての参考文献

参考書籍