Zenn
Closed3

LeetCode 296. Best Meeting Pointの解法

LeetCode
hard
esakaesaka

問題概要

Gridがあり、それぞれのセルは0か1
1は友達を表す
どこかのセルを待ち合わせ場所とする
全ての友達のマンハッタン距離での移動距離合計が少ないセル(その合計距離）を計算せよ
というもの

制約でGridの列・行がそれぞれ100くらいなので、愚直にワーシャルフロイドや各点からBFSやると時間足りない

esakaesaka

解法（列と行を別個に考える）

斜め移動はできないので、行と列を別に考えることができる

つまり、一度行だけで最適な行を選んだ後に、列を選ぶという方法がとれる

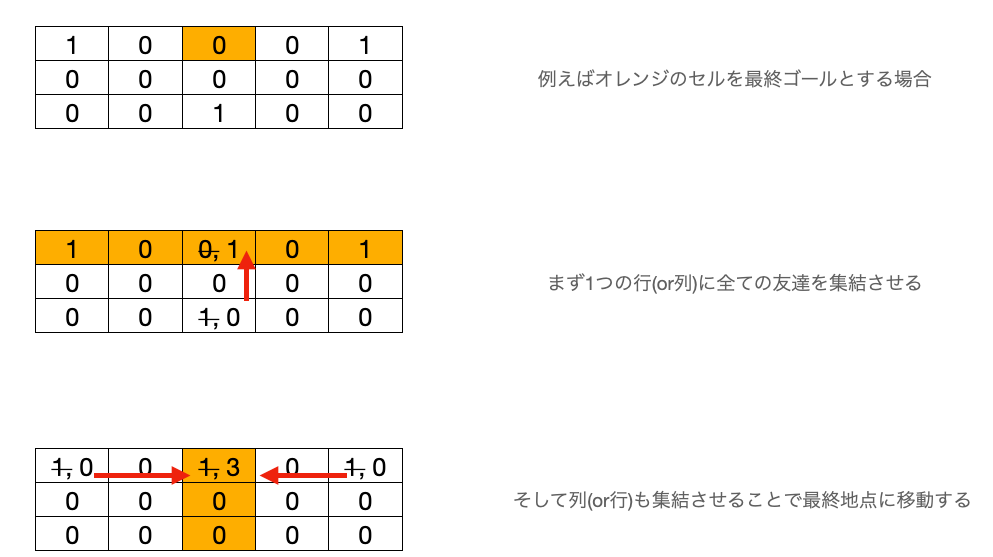
これだと (行の数x列の数) + (行の数x列の数)の計算量でいける

esakaesaka

解法詳細

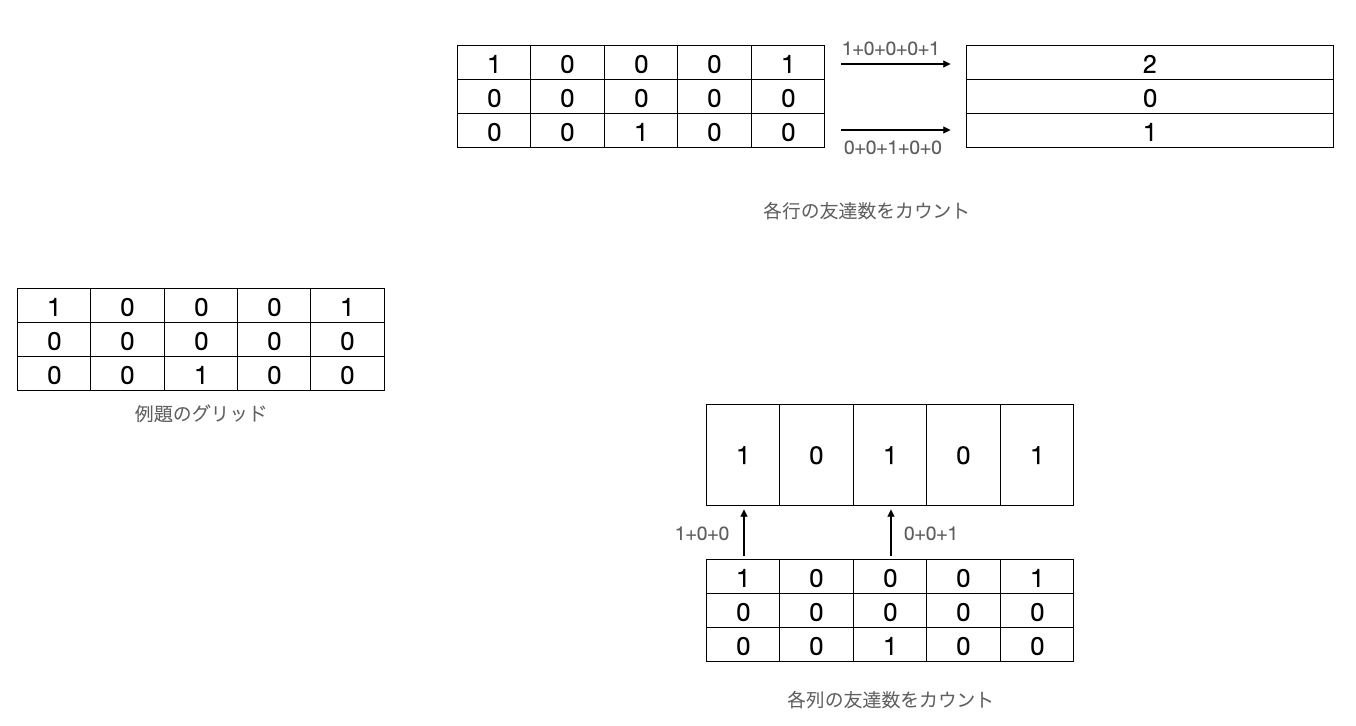
まず、列と行それぞれでの友達数をカウントする

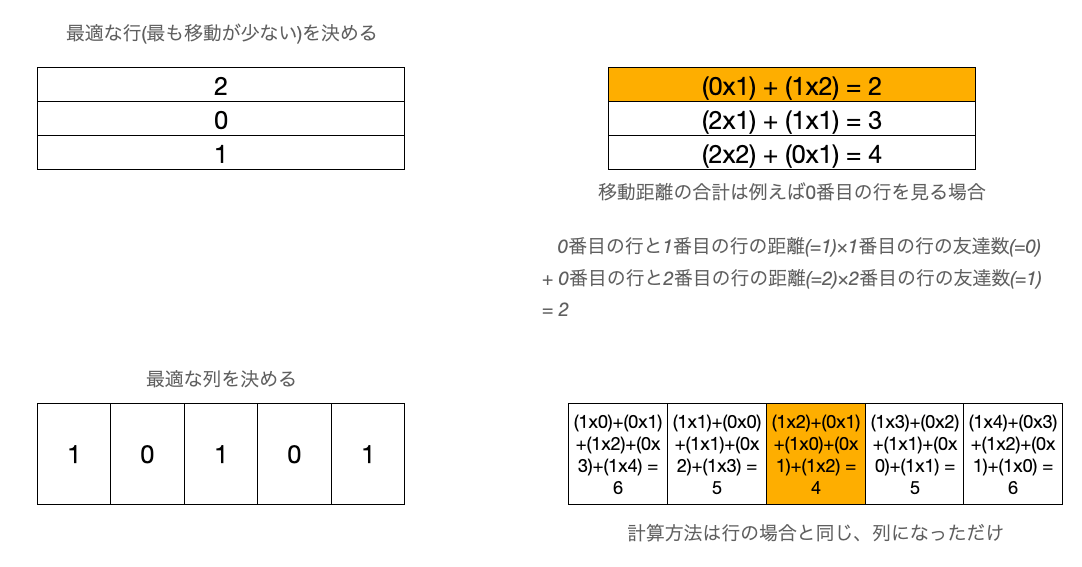
次に、行・列それぞれで、最適な行・列を決める
最適な行・列とは最も友達の移動距離が少ないもの

計算方法は
例えば0番目の行を見る場合

  0番目の行と1番目の行の距離(=1)×1番目の行の友達数(=0)
+ 0番目の行と2番目の行の距離(=2)×2番目の行の友達数(=1)
= 2

これを各行・各列に対して行う

最後に最適な行・列での移動距離を足し合わせると答えになる

コード

class Solution:
    def minTotalDistance(self, grid: List[List[int]]) -> int:
        countOfRow = [0] * len(grid)
        countOfColumn = [0] * len(grid[0])
        for i, row in enumerate(grid):
            for j, val in enumerate(row):
                if val == 1:
                    countOfRow[i] += 1

        for i in range(len(grid[0])):
            for j in range(len(grid)):
                if grid[j][i] == 1:
                    countOfColumn[i] += 1

        bestRow = sys.maxsize
        bestColumn = sys.maxsize

        for i in range(len(grid)):
            tmp = 0
            for j in range(len(grid)):
                if i == j:
                    continue
                tmp += abs(i-j) * countOfRow[j]
            bestRow = min(bestRow, tmp)

        for i in range(len(grid[0])):
            tmp = 0
            for j in range(len(grid[0])):
                if i == j:
                    continue
                tmp += abs(i-j) * countOfColumn[j]
            bestColumn = min(bestColumn, tmp)

        return bestColumn + bestRow

計算量

行の数=M
列の数=N
とした場合

時間計算量=O(NM), 空間計算量=O(N+M)

このスクラップは2022/01/30にクローズされました