AHC038 Tree Robot Arm 最終134位 解法
AHC 038お疲れ様でした。最終134位だった解法とそこまでの過程について述べます。(基本的により高順位の人の解法の方が役に立つと思いますが)誰かの参考になると嬉しく思います。
解法
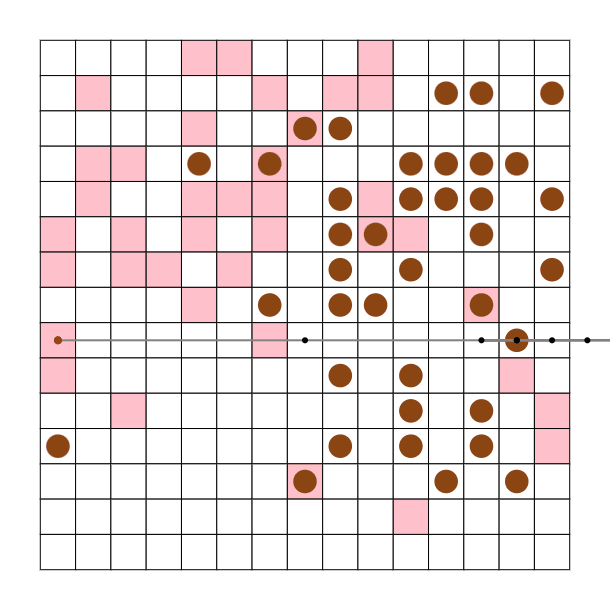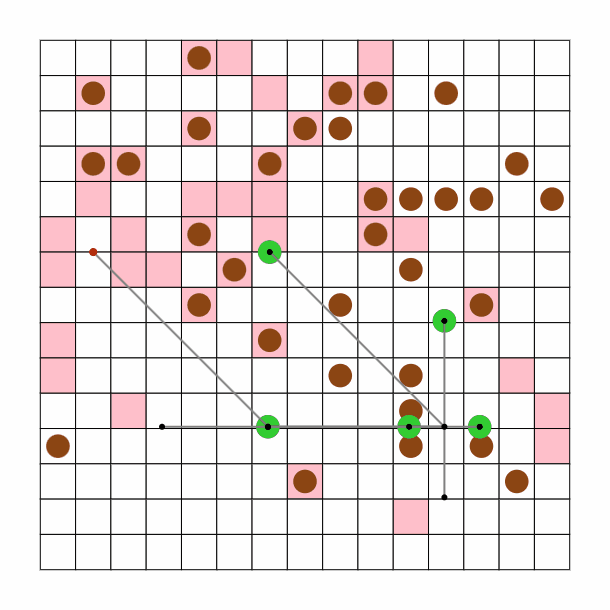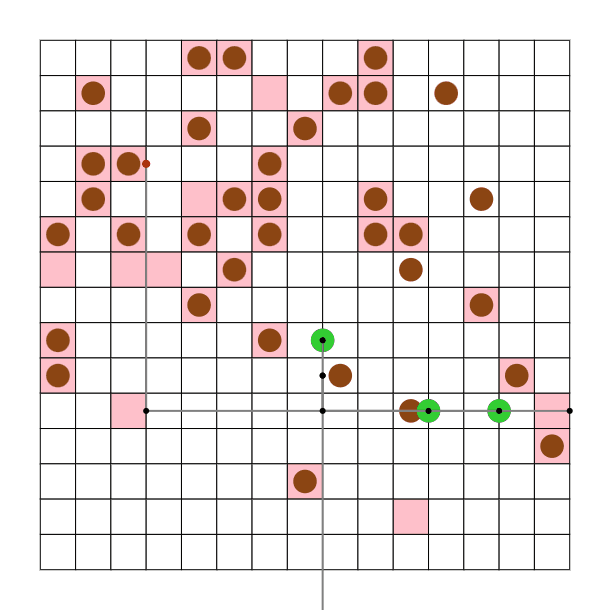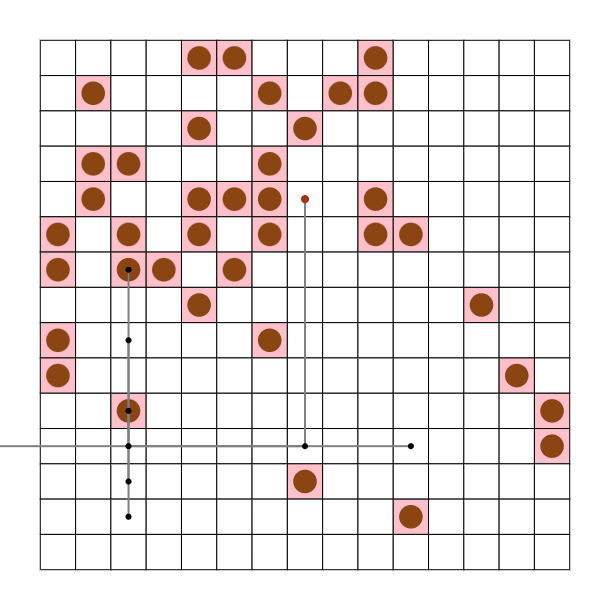
木の形、位置について
関節となる頂点が少なければよいと思ったので下記の様な形なるようにしました。マジックハンドのように一番最後の関節に指先がついています。
0 -> 1 -> 2 -> 3,4,5,6
関節は全頂点の
それぞれの長さは、「長くないと移動距離が必要になってしまうが長すぎるとほぼはみ出して使いにくい」と思ったので
初期位置は
実行時の戦略について
基本的に2つのステップに分けて操作しました。
最初のステップでは指先について、①回転しない②右回転③左回転 で掴んだり離せたりできる場合は掴んだり離したりを行います。(すでに目的地に置かれているたこやきは掴まない)
180度回転しない限り、損失をできるだけ生まずに進捗が得られるためです。
次のステップでは各指先のそのまま、右、左、180度回転の点の中で最も近い「たこやき」もしくは「目的地」(指先がたこやきを掴んでいるかどうかによる)を調べて、全部の候補の中から最も移動距離が少なくて済む方へ移動するという処理です。ここが最も重たい処理でした。
これらの動きが基本となるステップで、その処理の間に関節をランダムで回転させる処理を入れて数ステップ動かし、最も結果が良かったものを採用する、という処理を繰り返し最後まで行います。
上記をランダムで選んだ木・位置について実施し、最終的にスコアの高いものを出力しました。
実装について
最終的な操作は移動、回転、掴む・離すが一行で行われるため、どうやって実装すればよいか悩みました。実装する際は移動させたい、回転させたい、掴ませたい・離させたいが別々でやってくるので最初はこの実装で詰まっていました。
結果的に、それぞれの処理を独立して行い、評価を行いたいタイミングで依存関係を調べながら圧縮する(まとめられるものはまとめる)という方法を取ることで見通しが良くなりました。
運ばれるべきたこやきの座標や、まだたこやきが乗っていない目的地の座標はset<pair<ll,ll>>で管理し、利用するたびに削除しました。
戦略のセクションで書いた「ランダムで動かし結果が良かったものを採用する」という処理は、現在の頂点の位置やたこやきの位置、目的地の位置などすべてを持ったStructをコピーしシミュレーションする、という実装を行いました。ここのコピーのコストも多少重たかったのではないかと思います。
コピーを防ぐためには、操作を行ったあとロールバックする処理を書けば良いような気がしていましたがそこまで体力がありませんでした。
解法の変遷
とりあえず1個の点を動かしてみる

移動コストが半端ないので頂点をできるだけ増やす
頂点を増やせるだけ増やす

さっきより改善したが未だに移動コストが高い。回転を利用する。
回転した方がいいときは回転させる
ずっと点数が良くなる。このあたりから動きが予想できなくなり面白くなってくる。まだ関節要素を利用できていないので頑張って実装を行う。
関節をランダムで回転させ良いのを採用する
基本的にはこれ以上やることが思いつかず。ランダムで関節を回転させる時に、数手先を読んで比較したりすることで若干改善するもあとはパラメータ調整沼に落ちる。
反省・今後の課題・感想
今回選んだアプローチではランダムに設定する値が多い(初期位置、木の構造、長さ、いつ関節を回転させるか)一方で、一回スコアを得るまでの処理が重いため試行回数が稼げなかったため、制限時間の3秒間で効率的に解を探索できていないように感じました。(ほとんどの試行で解を更新できなかった。)
処理を軽くするか、ランダムで選んでいた値を、問題の考察を深めることで決め打てるようにする必要があったのではないかと思っています。特に上位陣の解法を見ると、
数日間は発生したバグに対する対処に時間を費やしていたため何度も心が折れそうになりました。実装力も課題です。
たこやきが整頓される様子をビジュアライザで眺めるのが楽しいコンテストでした。無事TLE・WAなくシステムテストも追加したのでお祝いにたこやきをスーパーで買おうかと思いましたが、想像以上に高く諦めました。
Discussion