📝

Megatron-LMを通して身につける分散学習の基礎

に公開
AI
GPU
分散学習
LLM
megatron
tech

論文タイトル：Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism
リンク：https://arxiv.org/pdf/2507.09466

※ 本ページの図は特筆がない限り全て本論文から引用しています。

執筆者：EQUES エンジニア　石橋悠生

はじめに

分散学習について勉強したいなと思い、その第一歩としてNVIDIAのMegatron-LM (2019)の論文を読んでみました。この記事はその解説であり、自分の備忘録でもあります。中級者向けの記事で理系大学生くらいなら理解できる内容になっているかと思います。また、一昔前の論文なので現在はアップデートされている部分もあると思いますが、分散学習の基礎として書いたものなので情報の新しさという点では他の記事を参考にしていただけると幸いです。

まずはMegatron-LMを理解するのに必要十分な程度機械学習、分散学習について説明しましたが、そこはわかっている、という方は読み飛ばしてもらっても構いません。

分散学習とは

当時、特に言語モデルなどの領域において、機械学習の学習データやパラメータが大規模化したことで、その計算処理が一台のGPUでは手に負えなくなってきていました。そこで複数台のコンピュータやGPUを用いて機械学習の処理を分散しよう、という発想に至りました。これが分散学習です。分散学習には大きく分けて以下の二つの分散方法があります。

  1. モデル並列
    機械学習における「計算」のパートを分割して複数のGPUで手分けする方法

  2. データ並列
    学習データを分割して各GPUに割り当て、各々で計算処理することで学習全体を高速化する方法

機械学習の全体像

分散学習の前にまずは機械学習の全体像に簡単に触れておこうと思います。機械学習のアルゴリズムは、どのAIモデルを使うかによって異なりますが、Megatron-LMの論文では特にTransferモデルという言語モデルに焦点が当てられていたので、Transferモデルの機械学習の流れを見ていきます。

特に「次に来る単語を予測すること」を目的とした場合の流れを考えます。

STEP 1: 学習データの準備

とにかくなんでも良いのでWikipedia, ニュース記事, 書籍やブログなどのインターネット上の人間が書いた文章を集めます。

（例：The cat sat on the mat ）

STEP 2: 入力処理

文章のままだと定量的に学習することができないので、数値（ベクトル）に変換します。

  1. トークン化: 文章を単語に分解（トークンと呼ぶ）

    The cat sat on the mat → [”The”, “cat”, “sat”, “on”, “the”]

    （“mat”は正解データとして一旦隠して学習させる）

  2. 埋め込み: 各トークンを埋め込みテーブル（巨大な辞書）を使って意味を表す初期ベクトルに変換

これにより “The cat on the”に、単語ごとに対応するような数値ベクトルが完成しました。

STEP 3: 思考プロセス

ここがTransformerモデルの核となる部分です。以下に示すAttention層とMLP層から成ります。

3-1: Attention層で文脈を理解

  • 目的：単語同士の関係性を理解して文脈を把握すること。
  • 処理：各単語のベクトルがAttention層に入力されると、単語ごとに、文中の他の単語との関連の強さが計算されます。
  • 結果：入力されたベクトルに対して、周りの単語との関係、文脈が考慮に入れられたベクトルが出力されます。

3-2: MLP層で深い思考

  • 目的：文脈付きのベクトルを元に、より高度で複雑なパターンを抽出すること。
  • 処理：Attention層で出力された文脈付きのベクトルが入力され、それに対して2回の線形処理と1回の非線形処理を行います。この処理を何十層も重ねて繰り返すことで、文章の意味をより深く思考することができます。
  • 結果：各単語のベクトルはさらに意味表現が豊かになります。

STEP 4: 最終予測（次の単語を当てる）

ここまでで学習した”The cat sat on the”のベクトルを元に次に来る単語を予測します。

  1. まず一番最後の単語”the”のベクトルを取り出します。

  2. これを特殊な線形層（出力層）に通して出力できる形式のベクトルにします。

  3. このベクトルから次に来る単語の確率分布を出力します。

    予測結果（例）：

    mat : 85%

    sofa : 10%

    floor : 4%

    …

STEP 5: 答え合わせとパラメータの修正

  1. 答え合わせ：予測された最も確率の高い単語（”mat”）と実際の正解の単語（”mat”）を見比べます。

  2. 誤差の計算：今回は正解だったので誤差の値（Loss）は小さくなります。ちなみにこの「誤差」は、一般的に**交差エントロピー誤差（Cross-Entropy Loss）**という関数で計算されます。これは、モデルが出した「確率分布（各単語の可能性）」と、「正解（matが100%で、他は0%）」という理想的な確率分布が、どれだけズレているかを測るものです。「自信を持って間違えた」ときほど、非常に大きな誤差（ペナルティ）を与えるという特徴があります。

  3. 逆伝播：この「誤差」の数値が今辿ってきたステップを遡るように伝わっていきます。

  4. パラメータの更新: 誤差が逆流する過程で、自動微分によって勾配（各パラメータをどちらにどれだけ動かせば誤差が減るかを示す値）が計算されます。

    この「パラメータ」とは、モデルを構成するすべての層に含まれる、学習可能な数値のことです。具体的には、

    • 単語埋め込みテーブル: 各単語の意味を表すベクトルの全数値。
    • アテンション層: Query, Key, Valueを作り出すための重み行列の中の全数値。
    • MLP層: 2つの線形層が持つ巨大な重み行列の中の全数値。

    といった、モデル内部に存在する何十億もの「重み」や「バイアス」の一つ一つを指します。

    この勾配に基づき、「この予測をするためには、あのアテンション層の行列のこの数値は0.3から0.31に、あのMLP層の行列のあの数値は-0.15から-0.16にすべきだった」というような、全パラメータに対する具体的な修正案が作られます。そして、その修正案に従って、モデル内の何十億もの数値がほんの少しだけ更新されるのです。

このSTEP1から5までをインターネット上の別の文章で何度も繰り返し行います。このサイクルを何兆回も行うことでこのTransferモデルはより精度の高い予測をできるようになります。

分散学習のアルゴリズム

機械学習において、計算処理を複数台のコンピュータや複数のGPUで分割して行うことを分散学習と言います。巨大なモデルにおいては一台のGPUやコンピュータにデータ量が収まりきらないことがあるため、そうした問題を解決することを目的として活用されます。

まずはMLP層の計算処理を例に、分散学習のアルゴリズムを簡単に説明します。

まず、前提としてMLP層は、入力されたデータ（行列）に対して自身の持つパラメータをつかって線形処理と非線形処理を順番に行うものとして考えられます。このとき全ての線形処理では入力された行列に対して重み行列をかけていると考えます。

ここで、例としてn列の列ベクトルxにAというn \times n正方行列を右からかける*という線形演算を行い、その後に値が正ならそのまま、値が負なら0にするReLUとよばれる非線形演算を行い、その後にまた右からBというn \times n行列をかけると言う線形操作を行うことを考えます。（この操作はTransformerモデルのMLP層の演算

（線形演算においてはデータ行列Xを行ベクトルデータの集まりとみなすか列ベクトルデータの集まりとみなすかで重み行列を右からかけるか左からかけるかが決まります。今回は行ベクトルデータの集まりとみなすので重み行列A, Bを右からかけます。）

例としては以下の3 \times 3行列を考えます。

入力データ:

X = \begin{pmatrix} 1 & -2 & 1 \\ -1 & 0 & -2 \\ 1 & 2 & 3 \end{pmatrix}

重み行列:

A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix}

重み行列:

B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & -2 \end{pmatrix}

この時Xに左からAをかけると

\begin{align} XA &= \begin{pmatrix} 1 & -2 & -1 \\ -1 & 0 & 2 \\ 1 & 2 & -3 \end{pmatrix} \end{align}

さらにこのYにReLUを作用させた結果をYとおくと

\begin{align} Y &= ReLU(XA)\\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 2 \\ 1 & 2 & 0 \end{pmatrix} \end{align}

Yに右からBをかけた結果をZとおくと

\begin{align} Z &= YB \\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & -4 \\ 1 & 4 & 0 \end{pmatrix} \end{align}

これで一連の処理が完了しました。こうした線形、非線形な処理を何度も行い、最終的に出てきた値を出力結果とします。さらにこの出力結果を正解データを比べ、誤差を小さくするように重み行列A, Bの要素の値を調整することで精度の高いモデルを構築します。

つぎに分散学習の第一歩として上記の一連の操作を分割して計算することを考えます。結論から言うと、これは重み行列を列ごと、行ごとに分解することで、その層において最後まで分解をした形のまま計算することができます。

Aを列ごとに分解して$A = \begin{pmatrix}
A_1 & A_2 & A_3
\end{pmatrix}$とすると

\begin{align} XA &= \begin{pmatrix} XA_1 & XA_2 & XA_3 \end{pmatrix} \end{align}

となり、重み行列Aをかけた結果のXAも列ごとに分解されて出力されます。あまり線形代数や行列に造詣のない方は実際に手を動かして計算すると、実際に上記のように行列積が列ごとに分解した結果と一致することがわかると思います。

さらにこのままReLUを作用させると

\begin{align} Y &= ReLU(XA) \\ &= \begin{pmatrix} ReLU(XA_1) & ReLU(XA_2) & ReLU(XA_3) \end{pmatrix} \end{align}

とできるので、列ごとに分解した状態でそれぞれの列の値においてReLUを作用させると良いことがわかります。

さらにこのYにおいて各列を

Y = \begin{pmatrix} Y_1&Y_2&Y_3 \end{pmatrix}

とした上で、Bを横方向に分解して

B = \begin{pmatrix} B_1 \\ B_2 \\ B_3 \end{pmatrix}

とすると

\begin{align} Z &= YB \\ &= \begin{pmatrix} Y_1&Y_2&Y_3 \end{pmatrix} \begin{pmatrix} B_1 \\ B_2 \\ B_3 \end{pmatrix} \\ &=Y_1B_1 + Y_2B_2 + Y_3B_3 \end{align}

と計算できます。

例えば、この一連の演算を、愚直にX \to XA \to ReLU(XA) \to Zと計算するよりも、上記のように分割して

GPU1: X \to XA_1 \to Y_1 = ReLU(XA_1) \to Y_1B_1

GPU2: X \to XA_2 \to Y_2 = ReLU(XA_2) \to Y_2B_2

GPU3: X \to XA_3 \to Y_3 = ReLU(XA_3) \to Y_3B_3

Z= Y_1B_1 + Y_2B_2 + Y_3B_3

と各GPUに割り振って計算させ、最後に足し合わせる方が速いことがわかります。単純に計算して0.03秒かかったとすると、理想理論上、各GPUでの計算はその3分の1で済むので0.01秒かかり、その上並列しながら計算することができるので結果全体の計算が0.01秒と、元の3分の1に短縮できることがわかります。

この巧妙な設計により、MLP層の前半の計算では、各GPUが他のGPUの計算結果を待つ必要がなく、独立して処理を進めることができます。そして、後半の計算を終えた最後の最後に、一度だけ全GPUで結果を集計（All-Reduceという通信）します。

これは非常に重要なポイントです。分散学習において最大のボトルネックになるのは、計算そのものよりもGPU間の通信（計算結果のやりとり）だからです。この通信の頻度を各計算ブロックの最後に1回という最小限に抑えることで、計算速度を劇的に向上させているのです。

このようにMLP層やAttention層において、行列をうまく分割しながら処理することで、分割した分だけ各GPUでの計算時間、計算量を減らすことができます。

Megatron-LMにおける革新性

ようやく本題の、Megatron-LMの説明に入ります。Megatron-LMの革新性は「優れた設計思想」と「それを実現するエレガントな実装」を提案したことという2つの柱に集約されます。

  1. Attention層の計算においても上に示した並列計算の手法が使えることを示したこと
  2. この並列計算をPyTorchを用いて、プログラムに数行書き足すだけで実現できることを示したこと

特に革新的である2のエレガントな実装について、次章でPyTorchの仕組みを含めて解説します。

PyTorchを用いたMegatron-LMの実装

まずはPyTorchを一般的にどう使うのかを説明します。PyTorchはPythonで使える機械学習のフレームワークの一つで、カスタマイズしやすく、アカデミックな領域において絶大な支持を受けています。PyTrochには以下に示すような様々なモジュールがあります。

モジュール名 役割と目的
torch PyTorchの基本ライブラリ。多次元配列であるテンソルを扱うための中心的な機能を提供します。NumPyに似ていますが、GPUでの高速計算が可能です。
torch.nn ニューラルネットワークを構築するための部品（層、活性化関数、損失関数など）がすべて詰まったモジュールです。モデルの「設計図」はこれを使って書きます。
torch.autograd 自動微分エンジン。順伝播の計算過程を記録し、逆伝播で必要となる勾配を全自動で計算してくれます。
torch.optim 最適化アルゴリズム（Adam, SGDなど）を提供するモジュールです。計算された勾配を元に、モデルのパラメータを効率的に更新する「勉強法」を決めます。
torch.utils.data 大規模なデータセットを効率的に扱うためのツールキットです。データをミニバッチに分割したり、シャッフルしたりする機能を提供します。
torch.distributed 分散学習をサポートするモジュールです。複数のGPUやコンピュータ間で、データの通信や同期を行うための機能を提供します。All-Reduceなどはここで定義されています。

まずはtorchとtorch.nnを用いてMLP層を作ることを考えてみましょう。

import torch
import torch.nn as nn

# torch.nn.Moduleを継承して、モデルの設計図を作成
# SimpleMLPという名前に設定.ここは任意の名前でOK
class SimpleMLP(nn.Module):
    # 1. 計算の部品を定義
    def __init__(self, input_size, hidden_size):
        super().__init__() # 継承
        # 一つ目の線形(Linear)演算. 上の例の重み行列Aに該当
        self.layer1 = nn.Linear(input_size, hidden_size)
        # GeLU(非線形演算). 上の例のGeLUに該当
        self.gelu = nn.GeLU()
        # 二つ目の線形(Linear)演算. 上の例の重み行列Bに該当
        self.layer2 = nn.Linear(hidden_size, input_size)

    # 2. 計算の流れを定義
    def forward(self, x):
        # 入力x -> layer1 -> gelu -> layer2 -> 出力
        x = self.layer1(x)
        x = self.gelu(x)
        x = self.layer2(x)
        return x

# 実際にモデルを使ってみる
my_model = SimpleMLP(input_size=10, hidden_size=20)
input_data = torch.randn(4, 10) # 4つの10次元データ
output_data = my_model(input_data)

print("出力データの形状:", output_data.shape)
# 出力: 出力データの形状: torch.Size([4, 10])

このコードは、入力された10次元のデータを、20次元に拡大し（layer1）、GeLUという非線形処理を行い、再び10次元に戻す（layer2）という単純なモデルです。重要なのは、forwardメソッドに書かれた通りの順番で計算が実行される点です。パラメータの学習（逆伝播）に必要な勾配計算は、PyTorchの自動微分（Autograd）エンジンがこの流れを元に全自動で行ってくれています。

次にMegatron-LM風のMLP層を設計することを考えてみましょう。Megatron-LMの設計思想ではAll-Reduceを効率的に行うためにf/g演算子というものを導入します。まずはその仕組みを理解するために以下のイメージ画像をみてみましょう。

モデル並列のイメージ画像 (出典：Shoeybi et al. (2019) "Megatron-LM”, Figure 3)

これは先ほど紹介した「分散学習のアルゴリズム」の内容を図式化したもので、自分が出した例では三分割で計算していましたが、この図では二分割の場合が示されています。ここでf/g演算子がそれぞれどう言った役割を持っているのかを説明します。結論からいえば下の表に示す通りになります。

関数 順伝播（予測の出力）での働き 逆伝播（パラメータの修正）での働き
f 恒等写像（何もせずにスルー） All-Reduce（勾配を合計）
g All-Reduce（出力を合計） 恒等写像（何もしない）

まず順伝播のときを考えてみましょう。TransformerのMLP層は、実際には2つの線形層から構成されています。Megatron-LMでは、1層目を列並列、2層目を行並列で分割します。

  1. 列並列: 各GPUは、入力Xと、列方向に分割された重み行列A_iを受け取り、中間結果Y_i = ReLU(X * A_i)を独立して計算します。この段階ではGPU間の通信は不要です。
  2. 行並列: 次に、各GPUは中間結果Y_iと、行方向に分割された重み行列B_iを使い、部分的な出力Z_i = Y_i * B_iを計算します。
  3. 集計: このままでは各GPUの結果は部分的なものなので、これらを足し合わせて最終的な正しい出力を得るために、g演算子によるAll-Reduceが必要になります。

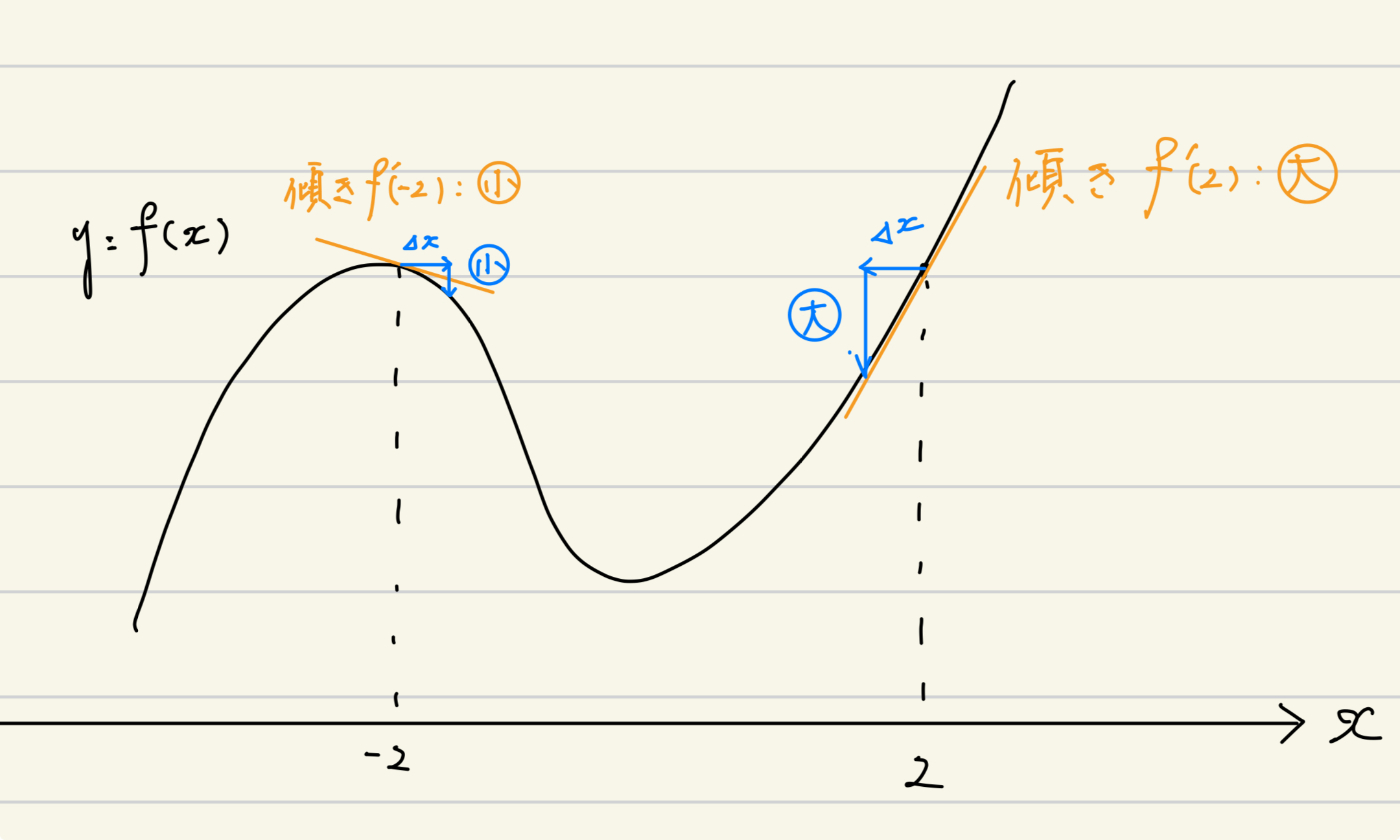
つぎに逆伝播の時を考えます。逆伝播では、最終出力の誤差を小さくするように、順伝播と逆の順番（Z \to Y \to X）で各パラメータ（BやAの重み）の勾配を計算していきます。ここで使われるのは自動微分というアルゴリズムで、これにより誤差関数の値を小さくするためには各パラメータをどのように変化させると良いかを調べます。「どうして微分？」と思う方もいるかもしれませんが、下図のように傾きを調べるとxを動かすとf(x)がどのくらい増えるのか、あるいは減るのかが分かりますよね？例えばx = 2において傾きが非常に大きくなっていますが、この時xを小さくするとf(x)の値は大きく減少します。

少し話がそれましたが、この微分計算の過程で、B_iの微分を計算したのち、A_iの微分を計算する前に一旦B全体で勾配の合計を取る必要があるので

B_i \to f(All-Reduce) \to A_iの順に計算します。図だけ見るとfが全体の最後になるような印象なので注意が必要です。

これを実装してみると以下のようになります。

import torch
import torch.nn as nn
import torch.distributed as dist
import os

# --- 分散環境の初期化 ---
# 一旦読み飛ばしてもOK
if 'LOCAL_RANK' in os.environ:
    local_rank = int(os.environ["LOCAL_RANK"])
    world_size = int(os.environ["WORLD_SIZE"])
    dist.init_process_group(backend="nccl", rank=local_rank, world_size=world_size)
    torch.cuda.set_device(local_rank)
else:
    local_rank = 0
    world_size = 1

# "f" の実装: Backwardで勾配をAll-Reduceする
# 可読性のためfを_AllReduceInBackwardという名前で定義
class _AllReduceInBackward(torch.autograd.Function):
    @staticmethod
    def forward(ctx, input_):
        # 順伝播では何もしない
        return input_

    @staticmethod
    def backward(ctx, grad_output):
        # 逆伝播で、受け取った勾配を全GPUで合計する
        dist.all_reduce(grad_output)
        return grad_output

# "g" の実装: Forwardで出力をAll-Reduceする
# 可読性のためgを_AllReduceInForwardという名前で定義
class _AllReduceInForward(torch.autograd.Function):
    @staticmethod
    def forward(ctx, input_):
        # 順伝播で、各GPUの出力を合計する
        dist.all_reduce(input_)
        return input_

    @staticmethod
    def backward(ctx, grad_output):
        # 逆伝播では何もしない
        return grad_output

# さっきのSimpleMLPと同じ構造のものをMegatronStyleMLPという名前で定義
class MegatronStyleMLP(nn.Module):
    def __init__(self, input_size, hidden_size):
        super().__init__()
        # world_sizeはGPUなどの計算機の個数
        # world_sizeで割って、分割する行列のサイズを決定
        self.hidden_size_per_partition = hidden_size // world_size
        
        self.layer1 = nn.Linear(input_size, self.hidden_size_per_partition)
        self.gelu = nn.GeLU()
        self.layer2 = nn.Linear(self.hidden_size_per_partition, input_size)
			
    def forward(self, x):
        # [工程1：列並列]
        x_parallel = self.layer1(x)
        x_parallel = self.relu(x_parallel)
        # 変更点 : 計算フローの途中に f と g を挿入 
        # [工程2：行並列の準備]
        # "f" を適用。順伝播では何もしないが、逆伝播で勾配を正しく集計する準備
        x_parallel = _AllReduceInBackward.apply(x_parallel)
        
        # [工程3：行並列]
        # 各GPUは部分的な結果を計算
        output_partial = self.layer2(x_parallel)
        
        # [工程4：結果の集計]
        # "g" を適用。順伝播で各GPUの結果を合計し、最終的な出力を得る。
        output_final = _AllReduceInForward.apply(output_partial)
        
        
        return output_final

★コードの解説

論文によると以下の数行を書き足せばいい、とのことでしたが実際に並列計算のアルゴリズムまで書くと少し冗長になってしまいました。

# 以下はfの定義。gの定義も同様にすればOKとのこと
class f(torch.autograd.Function):
def forward(ctx, x):
return x
def backward(ctx, gradient):
all_reduce(gradient)
return gradient

モデル構造の定義 (__init__)

まず__init__メソッドで、モデルの並列化設計を行っています。
hidden_size // world_sizeという行で、MLPの中間層のサイズを参加するGPUの総数（world_size）で均等に分割します。これにより、self.layer1は出力次元が分割された「列並列 (Column Parallel)」層、self.layer2は入力次元が分割された「行並列 (Row Parallel)」層となり、各GPUはモデルの一部分だけを持つ省メモリな構造が実現されます。

計算と通信のフロー (forward)

このモデルが正しく機能する核心は、forwardメソッド内の計算と通信のシーケンスにあります。

  1. [工程1：列並列]
    まず、全GPUが同じ入力xを受け取り、それぞれが持つ小さな重み行列self.layer1で独立して計算します。この時点ではGPU間の通信は発生せず、各GPUは部分的な計算結果x_parallelを保持します。
  2. [工程2 & 3：行並列]
    次に、この部分的な結果x_parallelは、2つの重要なカスタム関数_AllReduceInBackward (f) と _AllReduceInForward (g) を使って処理されます。
    • _AllReduceInBackward.apply(x_parallel): fの役割です。順伝播では入力をそのまま通すだけですが、逆伝播の際に勾配を全GPUで合計する「予約」のような役割を果たします。
    • output_partial = self.layer2(x_parallel): fを通過したテンソルを使い、次に行並列層self.layer2でさらに部分的な出力を計算します。
    • _AllReduceInForward.apply(output_partial): gの役割です。ここで初めてdist.all_reduceが実行され、全GPUが計算した部分的な出力output_partialを合計し、最終的な出力テンソルを完成させます。

まとめ

  1. 機械学習の全体の流れ
  2. 分散学習のアルゴリズム
  3. Megatron-LMの革新性
  4. PyTorchを用いた実装

の順番で解説をしていきました。

このブログのなかで特に力をいれて解説したのが分散学習のアルゴリズムの部分で、これはある程度大学数学に触れていれば理解できる範疇にあるので、できれば実際に手を動かして追ってみると良いと思います。また、論文中では、コンパイラに触れることなくPythonのコード上で少し修正を加えるだけでこの効率的な分散学習のアルゴリズムが実装できる、というところに特に重きが置かれていました。これに関しても元の論文をみたり解説記事を参考にして自分で実装してみると理解が深まるかもしれません。

おわりに

EQUESでは「最先端の機械学習技術をあやつり社会の発展を加速する」をミッションに研究開発と社会実装に取り組んでいます。一緒に事業を創出する仲間を募集しています。詳しくは以下をご覧ください。

https://www.wantedly.com/companies/company_6691299

Discussion